集中式自适应网格IMMJPDA算法

许江湖，刘 忠，党 玲

(1.海军工程大学 电子工程学院，湖北 武汉 430033;2.海军大连舰艇学院，辽宁 大连 116018)

1 概述

多传感器多目标跟踪是一项备受关注的研究课题，无论在军事领域还是在民用领域，都具有十分重要的理论意义和工程应用价值。多传感器多目标跟踪的关键问题是数据互联和状态滤波估计，其中有效方法主要集中在多模型(MM)算法和联合概率数据互联(JPDA)算法上。

多模型算法是机动目标跟踪算法中很受欢迎的方法。其主要思想是:设计一系列的模型来代表可能的系统行为方式或结构(称为系统模式)，基于每个模型的滤波器并行工作，系统的整体估计则是各模型滤波器所做估计的数据融合。大多数现存的MM估计算法，包括交互多模型(IMM)算法，在所有的时刻均使用预先确定的固定的模型集合，在这个意义上是具有固定结构(FS)的。固定结构多模型(FSMM)算法存在的缺陷是:为了覆盖现实环境中的大范围的可能的机动，算法所选的模型集合应该尽可能大。然而，增加模型的数量不但会引起计算量的增加，而且由于在当前时刻所使用的模型之间存在不一致会引起模型之间的不必要的竞争，因此未必能保证跟踪性能的提高。变结构多模型(VSMM)算法是近年内发展起来的最有效的机动目标跟踪滤波算法。该算法能克服FSMM算法的缺陷，且具有较高的费效比(即算法达到的性能和花费的计算量之比)。因此该算法从提出到现在，其在机动目标跟踪应用方面一直倍受关注［1－6］。

数据互联是多目标跟踪技术中最重要也是最困难的问题。近几十年，出现了许多数据互联方法，如最近邻域法、极大似然法、多假设法等。但这些算法在密集环境下，或在交叉、分叉及机动航迹较多的场合，将导致错、漏航迹相关。1980年，Bar-Shalomr提出了联合概率数据互联算法。该算法是杂波环境下对多目标进行数据互联的1种良好算法，一经提出便引起极大重视。然而，当目标进行机动时，单模型下的JPDA可能会失去对目标的跟踪。因此，IMM算法和JPDA相结合而产生的IMMJPDA算法能较好地解决多目标跟踪中的数据互联和状态滤波估计［7］这2个关键问题。国内外学者对该算法进行了相当多的研究和改进:文献［8］提出1种IMMJPDA的耦合滤波方法，该方法考虑了所有目标状态的相关性;文献［9］提出1种采用多次扫描的IMMJPDA算法以提高预测精度;文献［10］将D－S证据理论融入多传感器的IMMJPDA算法以使各传感器获得更精确的状态预测;文献［11］将广义S－D分配规则融入多传感器的IMMJPDA算法，获得了更高的跟踪精度;文献［12］将模糊算法融入多传感器的IMMJPDA算法中，显著提高了跟踪性能并有效地降低了周期耗时。由于上述文献对IMMJPDA的改进都没有涉及到IMM算法，也就是这些算法在多模型这个意义上都具有固定结构，因此，FSMM算法存在的缺陷这些算法都不可避免的存在。为此，本文将1种变结构多模型算法——自适应网格交互多模型(AGIMM)算法和JPDA算法相结合，提出了用于多传感器多目标跟踪的集中式自适应网交互多模型联合概率数据互联(AGIMMJPDA)算法。该算法通过自适应网格实现了模型自适应，从而以较小的模型集合覆盖了目标大范围的机动，并以此来克服固定结构IMMJPDA存在的缺陷。推导了该算法中的模型似然函数、互联概率和模型概率的计算方法，并通过计算机仿真结果显示该算法可以有效克服固定结构IMMJPDA算法存在的缺陷，并提高IMMJPDA算法的费效比。

2 问题描述

假设用q个传感器跟踪杂波环境中的N个目标，目标r(r=1，2，…，N)在k时刻使用的模型集合为Μk(r)={M1k(r)，M2k(r)，…，MJrk(r)}，Jr(r=1，…，N)表示目标r在k时刻的模型集合的长度。对于模型集合Μk(r)中第j个模型，目标r的状态和量测方程为:

3 AGIMM算法简介

AGIMM算法［2］从1个粗略的网格开始，然后在每个递归时间步根据1个自适应逻辑对网格进行调整，从而实现模型集合自适应调整。在协同转弯机动模型［17］的框架内，描述模型集合的网格设为转弯速率的连续间隔。AGIMM算法无需事先确定候选模型集合，特别适合系统可能的模型集合很大的情况。

4 AGIMMJPDA算法

为方便起见，这里假设传感器数目为2。本算法可以很容易推广到传感器数目大于2的情况。

各个目标都进行网格自适应调整后，分别按照各自的网格进行状态估计的交互、状态预测、传感器1的量测预测，量测确认。

式(3)的第一项可以写为:

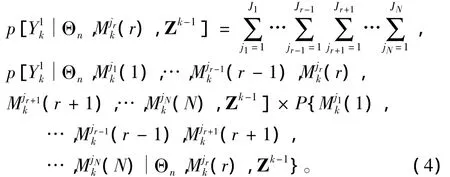
式(3)的第2项为联合事情Θn的先验概率:

式中:PD为传感器1的检测概率;ε为一常数。

假设基于过去量测的目标状态是相互独立的，则式(4)右边第一项可以写为:

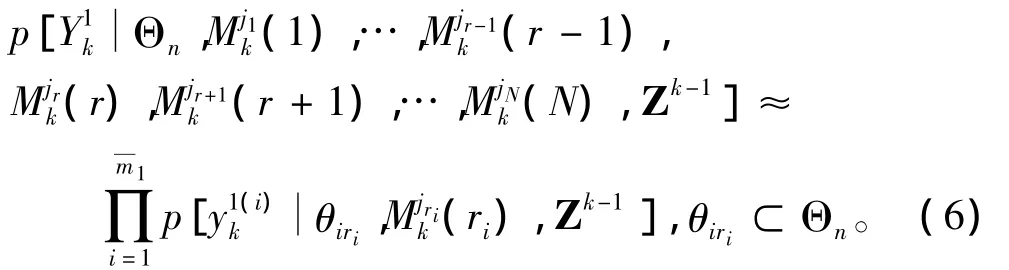
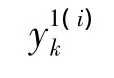
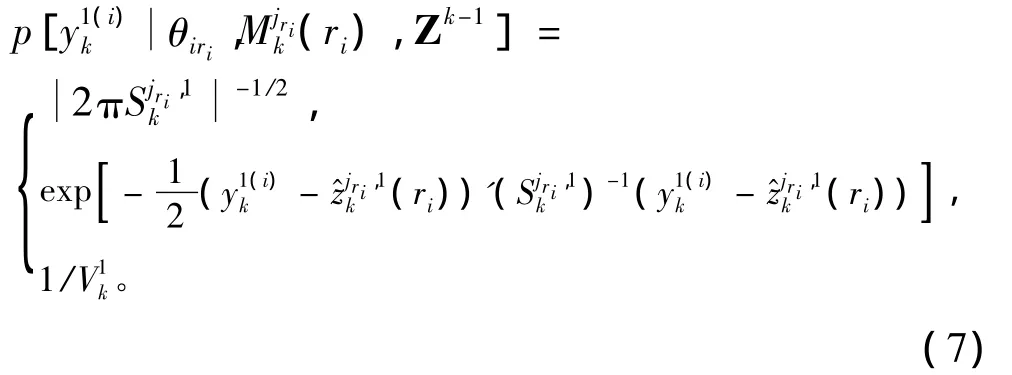
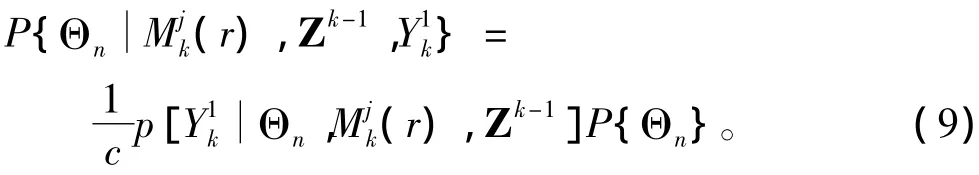
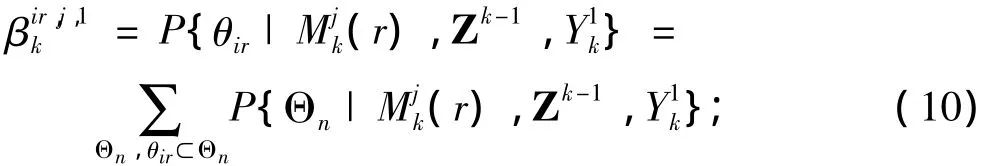
定义基于模型j和目标r的残差为

而组合残差为

Kalman增益为:

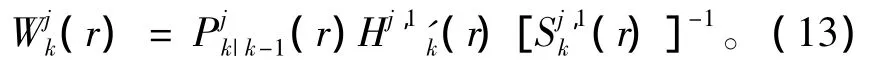
传感器1目标r基于模型j的状态估计及相应的协方差为:

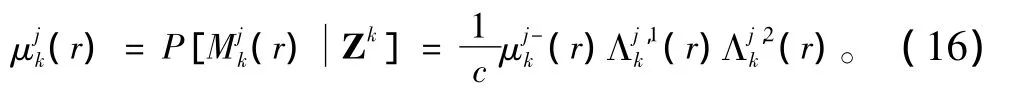
式中:c为归一化因子。目标r的总体估计及相应的协方差为:

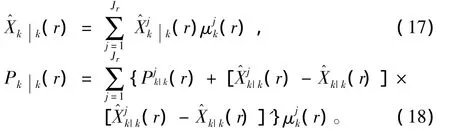
5 计算机仿真

这里的仿真情况考虑杂波环境下2个强机动目标的跟踪。仿真中采用的机动模型为协同转弯模型，但文献［13］的协同转弯模型是基于水平面的直角坐标系的，本文则考虑在某一固定高度的协同转弯模型，这样在式(1)中:

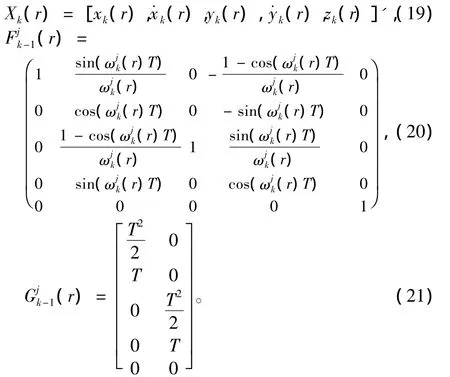
目标 1的初始状态为［50000，－172，55000，－246，40］'，机动想定为:在1 ～60 s，156 ～200 s，265～310 s，343 ～374 s，414 ～450 s，目标 1 作匀速直线运动;在 61 ～155 s，201 ～264 s，311 ～342 s，375 ～413 s，目标1分别作了4个180°转弯，转弯速率分别为1.87，－2.8，5.6，－4.68(°)/s。

目标2 的初始状态为［21000，172，10000，246，40］'，机动想定为:在 1 ～70 s，168 ～207 s，303 ～450 s，目标2 作匀速直线运动;在71 ～167 s，208 ～302 s，目标2分别作了2个180°转弯，转弯速率分别为－1.87，1.87(°)/s。2个目标在x－y平面的机动航迹如图1所示。

图1 目标机动航迹Fig.1 The true trajectories of the targets

传感器1(雷达)的量测数据为距离和方位角，传感器2(红外)的量测数据为方位角和仰角。距离r、方位角a及仰角e和直角坐标的关系分别为:

传感器1的量测误差的协方差为:

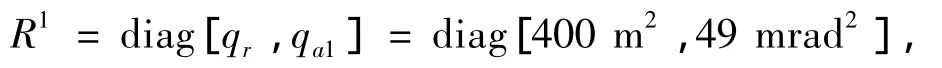
其中:qa1和qr分别为雷达方位角和距离的测量误差的方差。传感器2的量测误差的协方差为:

其中，qa2和qe分别为红外传感器的方位角和仰角的测量误差的方差。

采样间隔T=1 s，假设2个传感器的检测概率PD都为0.997。为了产生虚假量测，假设杂波服从泊松分布，其期望数量分别为 λ1=13×10－6/m·mrad(传感器1)和 λ2=5×10－4/mrad2(传感器 2)，确认区域的门限γ=16。

为比较本文提出的AGIMMJPDA算法和固定结构IMMJPDA算法性能，考虑3种固定结构IMMJPDA算法:FGIMM3JPDA、FGIMM5JPDA和FGIMM7JPDA。这里FGIMMn(n=3，5，7)表示使用由n个固定模型组成模型集合的固定网格IMM算法。这3种算法也采用顺序处理结构。FGIMM3JPDA使用的固定网格为 {－ 1.87°/s，0°/s，1.87°/s}，FGIMM5JPDA 使用的固 定 网 格 为 {－ 3.74°/s， － 1.87°/s，0°/s，1.87°/s，3.74°/s}，FGIMM7JPDA 使用的固定网格为 {－ 5.6°/s，－ 3.74°/s，－ 1.87°/s，0°/s，1.87°/s，3.74°/s，5.6°/s}。AGIMMJPDA 算法的初始网格为{－ 1.87°/s，0°/s，1.87°/s}。过程噪声标准差对于匀速直线模型为q1=1.8 m/s2，对于协同转弯模型为q2=2.5 m/s2。

进行了50次Monte Carlo仿真。图2所示为4种算法的滤波航迹，图3和图4分别为AGIMMJPDA、FGIMM5JPDA和FGIMM7JPDA算法对目标1滤波的位置和速度均方根误差，图5和图6分别为4种算法对目标2滤波的位置和速度均方根误差。表1为50次Monte Carlo各算法所用的时间。算法1～4分别代表 AGIMMJPDA、FGIMM3JPDA、FGIMM5JPDA 和FGIMM7JPDA。

从图2～图4可以看出，对目标1的跟踪过程中，FGIMM3JPDA在目标1的第3个转弯处(转弯率为5.6°/s)开始失去对目标1的跟踪，这是由于该处的转弯率已经大大超出FGIMM3JPDA所使用网格的覆盖范围;FGIMM5JPDA在该处出现了较大的误差，这是因为FGIMM5JPDA使用网格的覆盖范围虽然比FGIMM3JPDA大一倍，但相比于该处的转弯率仍有较大的差距;而FGIMM7JPDA和AGIMMJPDA算法对目标1跟踪具有相同的性能且优于FGIMM3JPDA和FGIMM5JPDA。这是由于FGIMM7JPDA的模型集合完全覆盖了目标的机动方式，而AGIMMJPDA通过自适应网格实现了模型集合自适应调整，也可以完全覆盖目标的机动方式。但从表1可以看出，AGIMMJPDA计算量比FGIMM3JPDA高出约7%，只有FGIMM7JPDA的24%，因此AGIMMJPDA可以提高IMMJPDA算法的费效比。

从图2、5、6可以看出，3种固定结构IMMJPDA算法对目标2的跟踪性能都与AGIMMJPDA相近。这是由于目标2的机动较为简单，3种固定结构IMMJPDA算法的模型集合都覆盖了其机动范围。从表1可以看出，FGIMM5JPDA计算量是FGIMM3JPDA的2.4倍，而 FGIMM7JPDA计算量则是 FGIMM3-JPDA的4.4倍。这说明对于固定结构IMMJPDA而言，增加模型的数量并不一定能提高性能，但计算量将急剧增加。

表1 50次Monte Carlo仿真各算法所用时间Tab.1 Computation time of 50 Monte Carlo simulation used by the algorithms

综合以上分析可知，对于IMMJPDA而言，其跟踪性能取决于预先设计的模型集合能否覆盖目标实际机动方式，当目标的机动方式超出模型集合的覆盖范围时，跟踪性能将下降，甚至可能失去对目标的跟踪;由于目标的机动方式一般是无法预知的，如果使用固定结构IMMJPDA算法，其预先设计的模型集合应该尽可能大，但随着模型集合规模的增大，固定结构IMMJPDA算法的计算量将急剧增大，同时并不能保证跟踪性能的提高。而AGIMMJPDA通过自适应网格实现模型集合自适应调整，可以完全覆盖目标的机动方式，并且其计算量略高于同等规模模型集合的固定结构IMMJPDA算法。因此，AGIMMJPDA可以有效地克服固定结构IMMJPDA算法存在的缺陷，并提高IMMJPDA算法的费效比。

6 结语

本文将一种变结构多模型算法——自适应网格交互多模型(AGIMM)算法和JPDA算法相结合，提出了用于多传感器多目标跟踪的集中式自适应网交互多模型联合概率数据互联算法，通过仿真显示该算法能有效提高IMMJPDA的费效比。如何将各种智能计算方法(如D－S证据理论、广义S－D分配规则、模糊算法、神经网络等)融入其中，从而进一步提高多传感器多目标跟踪技术的跟踪精度则是下一步的研究目标。

［1］VAHABIAN V，SEDIGH K A，et al.Optimal design of the variable structure IMM tracking filters using genetic algorithms［J］.Proceedings of the 2004 IEEE International Conference on Control Applications，2004，2(9):1485 －1490.

［2］党玲，许江湖，王永斌.自适应网格交互多模型算法［J］.火力与指挥控制，2004，29(4):51 －54.DANG Ling，XU Jiang-hu，WANG Yong-bin.Adaptive grid interacting multiple model algorithm［J］.Fire Control and Command Control，2004，29(4):51 －54.

［3］马海平，陈子栋.一种基于H∞滤波的模糊变结构交互多模型算法［J］.电子学报，2008，36(2):245 －249.MA Hai-ping，CHEN Zi-dong.Fuzzy variable structure interacting multiple model algorithm based on H∞filter［J］.Acta Electronica Sinica，2008，36(2):245 －249.

［4］杨丽娜，张剑云.一种改进的变结构多模机动目标跟踪算法［J］.弹箭与制导学报，2008，28(3):91 －94.YANG Li-na，ZHANG Jian-yun.An improved variable structure multiple modelmaneuvering targettracking algorithm［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2008，28(3):91 －94.

［5］刘高峰，顾雪峰，等.强机动目标跟踪的2种MM算法设计与比较［J］.系统仿真学报，2009，21(4):965 －968.LIU Gao-feng，GU Xue-feng，et al.Design and comparison two MM algorithms for strong maneuvering target tracking［J］.Journal of System Simulation，2009，21(4):965 －968.

［6］王亚利，等.基于Input Estimation的VSIMM机动目标跟踪［J］.系统仿真学报，2009，21(13):4143 －4148.WANG Ya-li，etal.Inputestimation based variable structure interactive multiple for maneuvering target tracking［J］.Journal of System Simulation，2009，21(13):4143－4148.

［7］李辉，沈莹，张安，等.交互式多模型目标跟踪的研究现状及发展趋势［J］.火力与指挥控制，2006，31(11):1 －4.LI Hui，SHEN Ying，ZHANG An，et al.The status quo and trend of target tracking based on in teractive multiplemodel［J］.Fire Control and Command Control，2006，31(11):1 －4.

［8］TUGNAIT J K.Tracking of multiple maneuvering targets in clutter using multiple sensors，IMM，and JPDA coupled filtering［J］.IEEE Transactions on Aerospace and Electronic Systems，2004，40(1):320 －330.

［9］PURANIK S，TUGNAIT J K.Tracking ofmultiple maneuvering targetsusingmultiscan JPDA and IMM filtering［J］.IEEE Transactions on Aerospace and Electronic Systems，2007，43(1):23 －35.

［10］张晶炜，修建娟，等.基于D－S理论的分布交互式多传感器联合概率数据互联算法［J］.中国科学(E辑:信息科学)，2006，36(2):182 －190.ZHANG Jin-gwei，XIU Jian-juan，etal.Distributed interacted multisensor joint probabilistic data association algorithm based on D － S evidence theory［J］.Science in China(Ser.E Information Sciences)，2006，36(2):182 －190.

［11］张晶炜，熊伟，等.集中交互式多传感器联合概率数据互联算法［J］.光电工程，2006，33(11):26 －30.ZHANG Jing-wei，XIONG Wei，et al.Centralized interacted multisensor joint probabilistic data association algorithm［J］.Opto-Electronic Engineering，2006，33(11):26 －30.

［12］张晶炜，何友，熊伟.集中交互式多传感器模糊联合概率数据互联算法［J］.电子学报，2008，36(8):1655 －1659.ZHANG Jing-wei，HEYou，XIONG Wei.Centralized interacted multiple model multisensor fuzzy joint probabilistic data association algorithm ［J］.Acta Electronica Sinica，2008，36(8):1655 －1659.

［13］LI X R，BAR-SHALOM Y.Design ofan interacting multiple model algorithm for tracking in air traffic control systems［J］.IEEE Transactionson ControlSystems Technology，1993，1(3):186 －194.

［14］何友，王国宏，陆大金，等.多传感器信息融合及应用［M］.北京:电子工业出版社，2007.HE You，WANG Guo-hong，LU Da-jin，et al.Multisensor InformationFusion With Applications［M］.Beijing:Publishing House of Electronics Industry，2007.