掺杂T型半导体量子线的量子限域效应与有效库仑作用

白凌志 王廷栋 刘 月 程 诚 张 伟 怀 平

（中国科学院上海应用物理研究所 上海 201800）

半导体纳米系统是相当活跃的前沿研究领域，Kapon等[1]于1989年制备了首个V型砷化镓量子线，2002年日本东京大学和美国Bell实验室的研究组改进了分子束外延(MBE)生长工艺、制备了T型砷化镓量子线[2]。相比于体材料半导体，半导体纳米材料的载流子在多个空间维度上受到限制，其态密度非常集中。理想的一维电子气系统的态密度在带底呈现E–1/2形状发散。根据自由电子理论的预测，半导体纳米材料的吸收谱强度正比于态密度，将在带边呈现尖锐的吸收峰[3]。

掺杂半导体量子线中形成的准一维系统是很有意义的研究领域[4–6]。若无掺杂，半导体量子线中的电子与空穴的浓度相同，即中性状态。观测表明，中性量子线的连续带吸收边并无发散行为，吸收强度主要集中在激子吸收峰[7,8]，表明量子线中载流子间的库仑作用将显著改变吸收谱的性质[9]。基于半导体布洛赫方程的计算表明，在一维中性状态电子-空穴系统的光吸收谱主要由激子吸收峰与减弱的连续带吸收谱构成，与自由电子理论所预言的发散行为不同。中性量子线的多体效应研究主要集中于费米边吸收及带隙重整化效应[10–12]。

在电荷掺杂的情况下，半导体量子线的吸收谱发生很大改变。东京大学Akiyama等[13]在n型掺杂的砷化镓量子线中发现了类似一维态密度形状的尖锐吸收边，以及激子(Exciton)和带电激子(Trion)的吸收峰。具有一维态密度形状的吸收边在一定温度下可与费米面的吸收峰同时存在。掺杂量子线的吸收谱中，复杂结构来源于准一维系统中的多种准粒子。接近带底的近自由载流子跃迁形成一维态密度形状的吸收边；电子与空穴形成中性准粒子，即激子；两个电子与一个空穴形成的准粒子为带电激子。

半导体中激子、带电激子及双激子等一系列准粒子是电子与空穴通过库仑作用构成的复合体[14]。库仑作用的强弱决定准粒子能否形成，库仑作用不仅受到载流子及准粒子的动态屏蔽而削弱，也受到量子限域效应、电荷掺杂的影响。理论计算表明，低维体系中的有效库仑作用随维度下降而明显增强，准粒子的束缚能也相应变大。严格的理论推导证明，如果半导体体材料的激子束缚能为E0=ħ2/(2mra02)，则理想半导体量子阱的激子束缚能为4E0[3]。实验与计算结果都表明半导体量子线的激子束缚能可达 5E0–6E0[15]。为理解掺杂半导体的准粒子及其光谱学特征，须阐明具有量子限域效应的准一维体系中电子、空穴间的有效库仑作用。在半导体量子线的理论研究中，包络函数近似法是计算量子线有效库仑作用的常用方法，但通常只考虑非掺杂的情况。本研究计算具有实际结构的n型掺杂T型量子线，并考虑有限势垒对载流子的约束，从而更好地理解准一维量子线中的多体效应。

1 理论模型

本文采用仅包含导带和重空穴带的理想两能带模型，并使用有效质量近似。基于有限元方法精确数值化求解一维量子线截面的薛定谔方程，在只考虑基态的情况下，通过包络函数近似获得载流子间的有效库仑作用。

1.1 薛定谔方程

图1(a)为具有T型结构的砷化镓(GaAs)量子线[13]，由相互垂直的两个量子阱构成，其中臂型量子阱(Arm well)厚6 nm，内部为砷化镓，外部为高掺杂铝的砷化镓(Al0.45Ga0.55As)；干型量子阱(Stem well)厚 14 nm，内部为低掺杂的砷化镓(Al0.07Ga0.93As)，外部为高掺杂铝的砷化镓(Al0.33Ga0.67As)。由于不同的铝掺杂率，两量子阱的界面处形成势阱，约束电子与空穴的迁移，使载流子只能沿着界面的延展方向(Z)自由运动，这是人工制备的半导体准一维结构。通过在距离干型量子阱100 nm处进行硅delta掺杂，可在干型量子阱中引入1011cm–2浓度的电子气；在臂型量子阱顶部加上电压，以调控进入准一维结构的电子气浓度，如图1(b)所示。电场沿–Y、Z方向为量子线的延展方向。

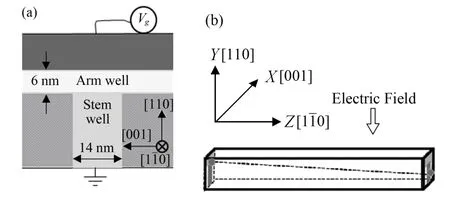
图1 n型掺杂T型量子线 (a)横截面示意图, (b)侧视图Fig.1 Schematics of an n-doped T-shaped quantum wire. (a)Cross section view, (b) Side view

铝掺杂砷化镓的势能(meV)经验公式为[16]，

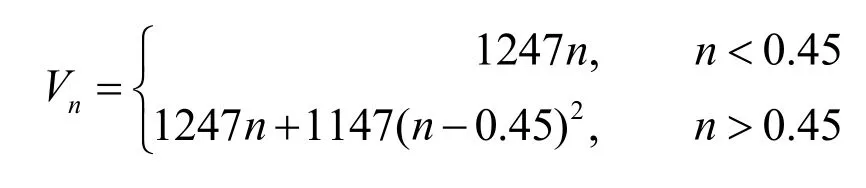
其中，n是掺铝砷化镓(AlnGa1–nAs)的铝掺杂率。量子线横截面处载流子的薛定谔方程为：

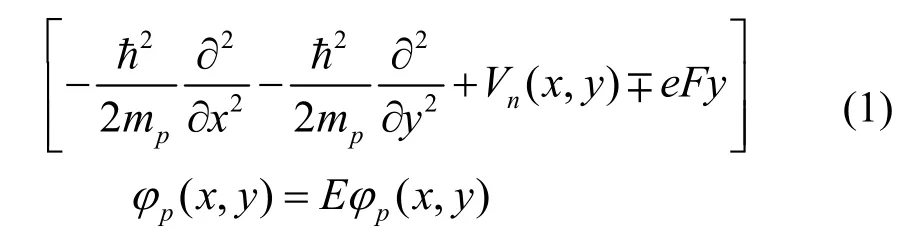
其中，mp为载流子有效质量，载流子为电子(e)和空穴(h)，即me与mh分别是砷化镓体材料中电子与空穴的有效质量;φp(x,y)是载流子波函数；E是载流子单粒子基态能量；Vn(x,y)是掺杂砷化镓相对于无掺杂砷化镓的势能，n是铝的掺杂率；e是单位电荷，F是控制掺杂的电场场强。在此模型中，电场的场强决定从量子阱注入量子线的载流子浓度。当载流子为电子时，受力与电场方向相反，式(1)中电势能项eFy前符号取“–”，电子从干型量子阱向臂型量子阱移动；当载流子为空穴时则相反，空穴受电场力从臂型量子阱向干型量子阱移动。

1.2 波函数数值求解

式(1)中的二阶偏导算符可用中心差分格式离散化为：

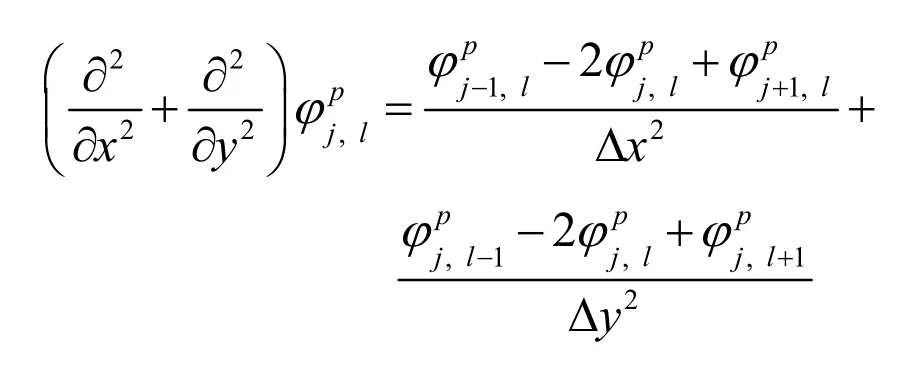
因此可得到所求区域内部格点差分格式的线性方程组。对于边界格点，因所求单粒子基态波函数可认为是光滑缓变的函数，故采用等值外推法确定边界条件，由上述二阶差分格式及式(1)可得边界格点的离散化的线性方程组，与内点的线性方程组合起来可得相应的系数矩阵。用 Householder法进行矩阵对角化计算，得到所求基态的单粒子波函数及能量。φ的上标p代表电子(e)与空穴(h)，下标j,l分别是x和y方向上离散化的格点序数。

为确保计算精度，数值求解区域为干型量子阱与臂型量子阱T形相交所成矩形的3倍。计算参数为：干型量子阱宽Dx=14 nm，臂型量子阱宽Dy=6 nm，介电常数ε0=13.74，电子有效质量me=0.0665m0，空穴有效质量mh=0.457m0，m0是电子真空质量。砷化镓体材料激子玻尔半径a0=12.5 nm和对应的激子束缚能E0=4.2 meV分别作为长度单位和能量单位。

求解式(1)式可采用变分法、有限元法等。变分法计算量小，是半导体多体理论计算中常用方法，但因猜测复杂边界条件的波函数困难，不适于讨论具有真实结构的量子线的情况。Szymanska等[16]用快速傅立叶变换法计算了 T型量子线中的激子波函数，计算精度高且可适应于各种边界条件的量子线，但其仅讨论了非掺杂情况。本文用有限元方法求解薛定谔方程，以便处理各种复杂边界条件及掺杂情况，但计算量较大。实际求解区域大小是准量子线截面面积(14 nm×6 nm)的3倍。若用4或5倍量子线横截面积作为数值求解区域，所得波函数数值误差可小于5%，但计算量明显增加。

1.3 有效库仑势

根据包络函数近似[17]，设p,q=e,h，则准一维量子线中载流子间的有效库仑势Vp–q(z)为：

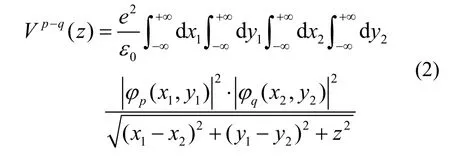
其中，(x1,y1)与(x2,y2)分别为两个相距为z的截面的横向坐标，φp(x1,y1)和φq(x1,y1)分别为载流子的基态波函数，ε0与e分别是介电常数和基本电荷。对实空间的有效库仑势在空间作傅立叶变换得到，

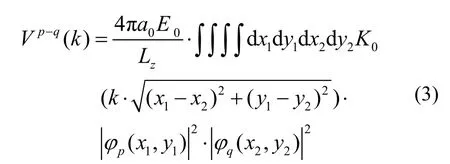
式中，Lz是量子线沿伸展方向z的长度，K0(r)是零阶第二类修正Bessel函数，其在r→0时呈对数发散K0(r)→–lnr，在长波极限k→0时，有效库仑势的渐进行为是V(k)→–lnk+Constant。因此，由(3)式积分计算载流子间有效库仑势时，须用解析方法防止发散。本文分别计算n型掺杂T型量子线中载流子间的有效库仑势Ve–e、Vh–h与Ve–h。

2 结果与讨论

2.1 载流子基态密度分布

图2(a)、2(b)为n型掺杂T型砷化镓量子线的基态电子密度分布。采用等高线标识密度，由内至外依次等值减小。无外加电场时，电子主要分布在T型量子线内，即干型量子阱与臂型量子阱的界面区域。由于臂型量子阱未掺杂，势能较低，电子易向其扩散；干型量子阱为低掺杂，势能较高，仅有少量电子能进入。在受限体系中如尺度D接近粒子的德布罗意波长，根据测不准原理，电子平均最小动量为ħ/D。因此，电子的平均动能伴随尺度减小而增加。电子动能增至接近势垒时，量子隧穿效应导致电子从受限体系中泄漏。电子泄露会削弱量子限域效应，不利于形成一维电子气。由图2(b)，当加上一定的控制电场后，电子云向电场反方向移动，在干型量子阱中收缩，并向臂型量子阱中扩展。

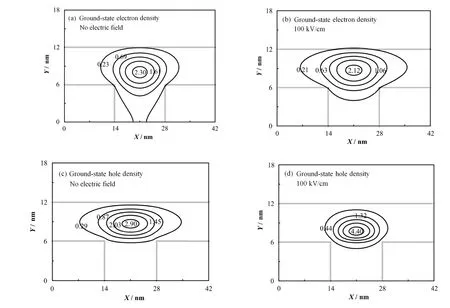
图2 不加电场与加100 kV/cm电场下n型掺杂T型量子线的基态电子(a, b)和基态空穴(c, d)的密度分布)Fig.2 Ground-state electron (a, b) and hole (c, d) density in n-doped T-shaped quantum wire, with or without electric field.

n型掺杂T型砷化镓量子线的基态空穴密度分布见图2(c)、2(d)。无外加电场时，空穴的基态密度分布不同于电子。空穴的有效质量约为电子的 7倍，同样尺度下，其平均动能较小，易在臂型量子阱中形成定域状态，而难以进入干型量子阱。从图2(d)可见，当外加电场后，空穴在臂阱里逐渐收缩，几乎局域在T型量子线中心，并沿电场方向往干型量子阱略微移动。

2.2 有效库仑势

利用电子与空穴的基态波函数，本文用包络函数近似计算载流子间的有效库仑作用。图3给出了k空间中n型掺杂T型量子线的电子-电子及空穴-空穴间有效库仑势。为讨论掺杂对库仑作用的影响，对比了3种电场强度下库仑势的变化规律。由图3，有效库仑势在长波极限k→0时均呈对数发散，这是一维系统库仑作用特点。三维系统的库仑作用呈现k–2发散规律，而二维系统则呈现k–1的发散规律。伴随维度下降，k空间中有效库仑势的发散趋于减弱，即实空间的维度越高库仑作用的长程特性越显著。而当k→∞时,有效库仑势一致趋向于零。

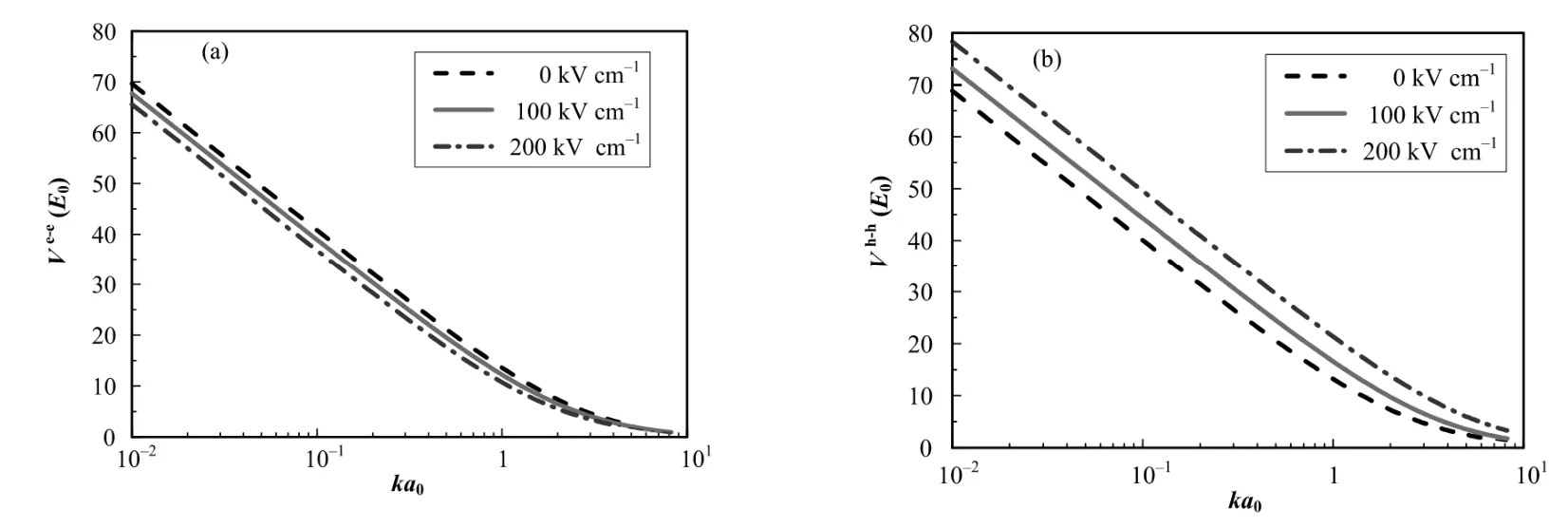
图3 n型掺杂T型量子线的有效库仑势 (a) 电子-电子，(b)空穴-空穴Fig.3 Effective Coulomb potentials in n-doped T-shaped quantum wire. (a) e-e, (b) h-h

电子间的有效库仑作用随电场的增加而减弱，空穴间的有效库仑作用则变强。由于电子受力与电场方向相反，电子在强电场作用下从量子线进入臂型量子阱。量子线中电子密度的降低减弱了有效库仑作用；而空穴受到电场力的作用从臂型量子阱向干型量子阱移动，但由于受到干型量子阱势垒的阻挡，空穴密度集中在界面处的量子线中，增强了库仑作用。

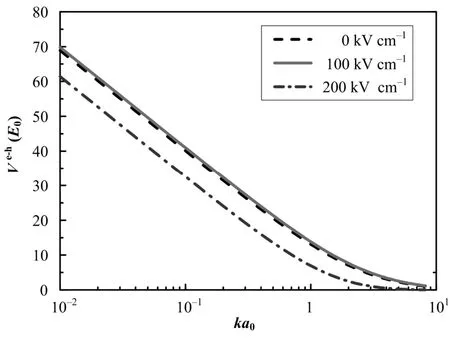
图4 n型掺杂T型量子线内电子与空穴间有效库仑势Fig.4 Effective Coulomb potential between electron and hole in n-doped T-shaped quantum wire.

图4为n型掺杂T型量子线内电子与空穴间有效库仑势。电子-空穴间有效库仑势随电场增强先增后减。根据包络函数近似，有效库仑势强度同时与电子与空穴的基态波函数相关。从基态波函数的计算中得知，前者在电场作用下离域，而后者变得局域,两者共同竞争作用的结果较为复杂。当电场较弱时，由于电子的动能较大，主要受到影响的是空穴，即空穴密度变得集中。电子-空穴有效库仑势与图3(b)中空穴-空穴有效库仑势的变化规律一致。而当电场较强时，电子明显向臂型量子阱中扩散，降低了量子线中的电子密度；且空穴得到足够大的电场势能后有可能克服势垒进入干型量子阱中，同时降低了量子线中的空穴密度。这两个效应叠加，使电子-空穴有效库仑势明显降低。

3 结语

本文用双带模型研究n型掺杂T型砷化镓量子线的量子限域效应与有效库仑势。用有限元法数值求解复杂边界条件下薛定谔方程，获得T型砷化镓量子线中电子与空穴的单粒子波函数。量子线的掺杂效应由外加电场控制。计算结果表明，电子有效质量轻，易突破有效势垒的约束，从量子线进入臂型量子阱，离域性较强；而重空穴的有效质量大，局域性较强。用包络函数近似，计算了不同场强下e-e、h-h及 e-h间的有效库仑作用。三种有效库仑势在长波极限下均呈对数发散，反映了准一维系统与高维的不同特征。随着外加电场增强，空穴间的库仑作用增强，电子间的库仑作用则减弱。电子与空穴间的库仑作用变化规律较为复杂，显示了电子与空穴在掺杂情况下局域与离域趋势相互竞争的特点。应当指出，本文的计算虽考虑了电子与空穴在横截面处的分布，但未考虑掺杂系统中的多体效应对库仑作用的影响。半导体量子线中载流子的屏蔽作用将明显削弱有效库仑作用，为处理这样的多体屏蔽效应，须用格林函数理论作进一步研究。

1 Kapon E, Hwang D M, Bhat R. Stimulated emission in semiconductor quantum wire heterostructures[J]. Phys Rev Lett, 1989, 63(4): 430–433

2 Yoshita M, Akiyama H, Pfeiffer L N,et al. Quantum wells with atomically smooth interfaces[J]. Appl Phys Lett, 2002, 81(1): 49–51

3 Haug H, Koch S W. Quantum Theory of the Optical and Electronic Properties of Semiconductors[M]. 2nded.World Scientific, Singapore, 2004

4 Langbein W, Gislason H, Hvam J M. Optimization of the confinement energy of quantum-wire states in T-shaped GaAs/AlxGa1-xAs structures[J]. Phys Rev, 1996, B54(20):14595–14604

5 Glutsch S, Bechstedt F, Wegscheider W,et al. Excitons in T-shaped quantum wires[J]. Phys Rev, 1997, B56(7):4108(7)

6 Rodríguez F J, Tejedor C. Optical singularities in doped quantum-well wires[J]. Phys Rev, 1993, B47(3):1506–1515

7Wegscheider W, Pfeiffer L N, Dignam M M,et al. Lasing from excitons in quantum wires[J]. Phys Rev Lett, 1993,71(24): 4071(4)

8 Rossi F, Molinari E. Coulomb-induced suppression of band-edge singularities in the optical spectra of realistic quantum-wire structures[J]. Phys Rev Lett, 1996, 76(19):3642(4)

9 Ogawa T, Takagahara T. Optical absorption and sommerfeld factors of one-dimensional semiconductors:An exact treatment of excitonic effects[J]. Phys Rev, 1991,B44(15): 8138–8156

10 Chow W W, Koch S W. Semiconductor-Laser Fundamentals[M]. Springer, Berlin,1999

11 Huai P, Ogawa T. Absorption and gain spectra of optically excited semiconductor quantum wires: effects of coulomb correlation and screening[J]. J Lumin, 2006, 119–120:468–472

12 Huai P, Akiyama H, Ogawa T,et al.Coulomb enhancement and suppression of peak gain in quantum wire lasers[J]. Jpn J Appl Phys, 2007, 46(44):L1071–L1073

13 Ihara Toshiyuki, Hayamizu Yuhei, Yoshita Masahiro,et al.One-dimensional band-edge absorption in a doped quantum wire[J]. Phys Rev Lett, 2007, 99(12): 126803(4)

14 Hayamizu Yuhei, Yoshita Masahiro, Akiyama H,et al.Biexciton gain and the mott transition in GaAs quantum wires[J]. Phys Rev Lett, 2007, 99(16): 167403(4)

15 Rinaldi R, Cingolani R, Rossi F,et al. Exciton binding energy in GaAs v-shaped quantum wires[J]. Phys Rev Lett, 1994, 73(21): 2899(4)

16 Szymanska M H, Littlewood P B, Needs R J. Excitons in T-shaped quantum wires[J]. Phys Rev. 2001, B63(20):205317(14)

17 Wang D W, Sarma S Das. Many-body effects on excitonic optical properties of photoexcited semiconductor quantum wire structures[J]. Phys Rev, 2001, B64(19): 195313(16)