碎石混凝土灌注桩强度的可靠度研究

刘少东，解国梁，郑鑫

（黑龙江八一农垦大学，大庆163319）

在弹性介质中传播的纵波声速CP按下式计算：

式中：E——弹性模量

ν——泊松比

ρ——介质密度

可以看出，对于等级不同的混凝土，其弹性模量各不相同，声波在其中传播的速度也不相同。通常，弹性模量高的混凝土越密实，声波在其中传播的速度也就越快。同时，混凝土弹性模量与强度也有显著的相关关系——混凝土弹性模量越大，其强度也越高。对于混凝土材料而言，由于波速和强度之间存在这种内在联系，因此可以通过波速检测推求混凝土强度。基于这一基础，采用超声波法检测混凝土强度的研究活动正在积极开展，检测技术实践应用也日益广泛。但是，目前规范的制定远远滞后于科研进展与实践应用，我国尚未形成超声波法检测混凝土强度的规范和标准，仅在部分发达地区（如广东、上海等）形成了地方标准。为推动超声波法检测混凝土强度规范和标准的形成，大量的试验研究和工程实践经验必不可少，因此在全国范围内广泛开展超声波检测混凝土强度的研究是十分必要的[1]。近年来，我国经济社会发展迅速，建筑行业结构检测技术升级换代要求十分强烈，因此，不断完善结构强度的超声波检测方法，建立相应的规范和标准用以指导工程实践十分必要。灌注桩是应用于高层建筑的重要基础类型，其施工方法是采用特定的工艺在现场钻孔，然后在孔内浇筑混凝土成桩。由于灌注桩成桩质量受多种因素的影响，其质量检测一直是工程施工中非常关注的问题。目前，灌注桩的成桩质量测定广泛使用超声波法，但该方法通常用于研究灌注桩的承载力可靠度[2]。由于不能明确主要变量，目前还不能利用该项技术定量分析桩身强度，但可以利用该方法对灌注桩桩身混凝土强度的可靠度进行研究。本文选择C20、C25、C30、C40等四个不同等级的混凝土试块，用超声波测强法对这些试块进行检测，建立了不同等级混凝土的波速-强度曲线方程。结合曲线方程和实测波速取得灌注桩计算强度，对计算强度和实测强度进行偏差分析，并结合现场灌注桩试块实测强度推求桩身强度的可靠度。通过此项研究，可望为混凝土灌注桩的“声速—强度”方程的建立提供依据。

1 建立波速—强度曲线方程

1.1 混凝土立方体标准试块纵波速度检测

根据工程实践经验[3]，选择混凝土强度等级为C20、C25、C30、C40，尺寸为150mm×150mm×150mm立方体标准试块（与实际灌注桩的强度等级一致），每一强度等级制作3个试块，四个强度等级共计试块12个。混凝土原料选用强度等级为425的普通硅酸盐水泥、最大粒径不超过40mm的碎石及中砂。所有试块均在标准养护条件下养护28天，然后分别对每个试块进行声参量测试和强度试验，试验数据如表1所示。声参量测试将小型径向换能器贴在试块相对侧边的对称位置上，每个试块检测3对对称点位的振幅及首波声时。取得声波参数后，在压力机上做强度试验，测取试块抗压强度值。对每个试块3对测点的波速数据按下式计算均值及标准差：

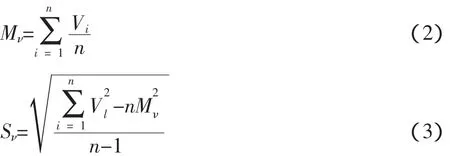
经计算，Sν处于0.06～0.12 km·s-1区间内；速变异系数：Cν=Sν/Mν，处于0.013～0.037区间内。

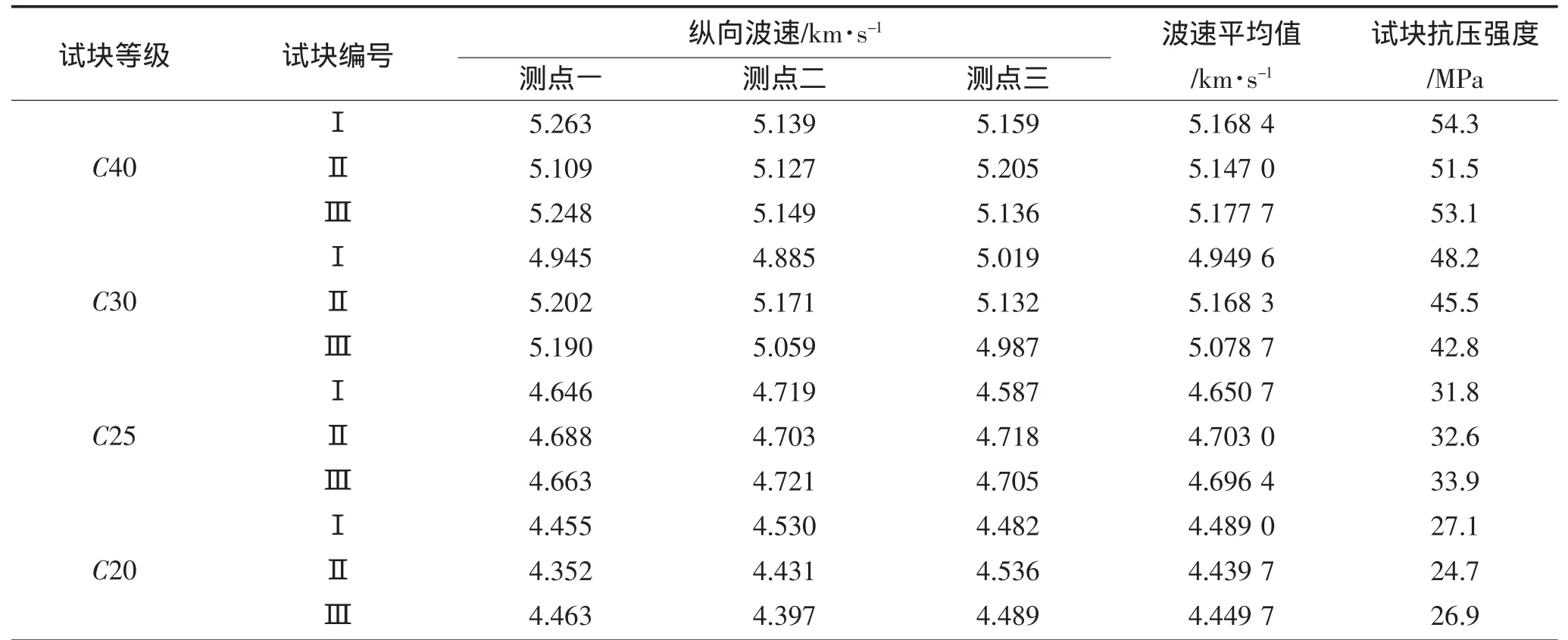
表1 实测纵向波速和试块强度值Table1 Table ofmeasured velocity and strength of testblock

1.2 试验结果分析

为取得“波速—强度”关系的曲线方程，分别采用幂函数、指数函数及对数函数模型对试验数据进行非线性回归分析。考虑到用拟合曲线方程计算混凝土试块强度会产生误差，对预计产生的误差用式（4）进行计算。

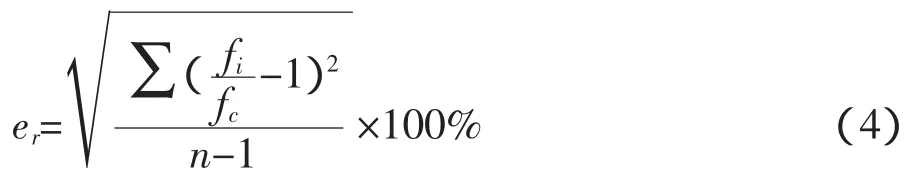
式中：fi——试块强度实测值；

fc——试块强度计算值，用实测波速代入拟合曲线方程可得；

n——试验试块个数。

（1）幂函数模型拟合结果为：

回归方程相关系数r为0.942 7。按公式（4）计算得er=6.59%＜12%，满足规范要求。

（2）指数函数模型拟合结果为：

回归方程相关系数r为0.940 8，er=7.59%＜12%，满足规范要求。

（3）对数函数模型拟合结果为：

回归方程相关系数r为0.920 7，er=8.32%＜12%，满足规范要求。

（4）抛物线模型拟合结果为：

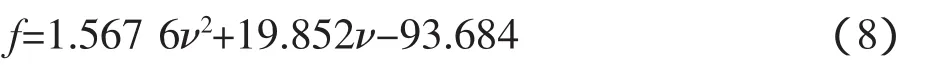
回归方程相关系数r为0.921 4，er=9.14%＜12%，满足规范要求。

2 拟合曲线方程的可靠度计算

在现场钻取大量灌注桩试块（设计强度等级为C25）并进行了强度检测，按照统计分析的要求，求得这些试块的抗压强度平均值为32.6 MPa，标准差为3.075 648 MPa；同时，测取了大量实测的灌注桩桩身波速数值（如表2所示），求得波速均值为4.64 km·s-1，标准差为0.164 523 km·s-1。

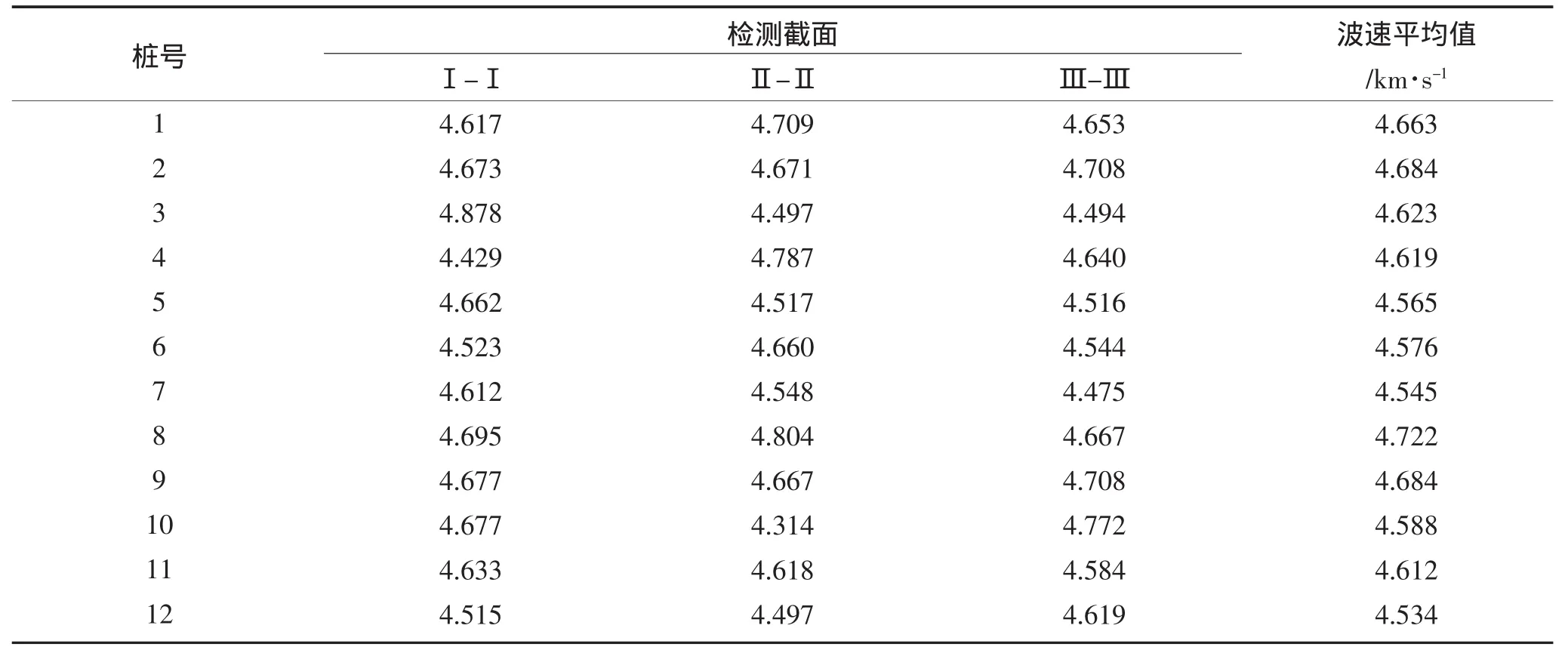
表2 灌注桩身的实测波速Table2 Table of the measured velocity of bored piles

通过上述非线性回归分析得到4个不同函数模型的曲线方程，将这些曲线方程与灌注桩检测实测数据相结合，将实测桩身波速逐一代入式（5）、（6）、（7）、（8）可得灌注桩桩体计算强度，并以现场灌注桩试块强度实测数据为基准，分别验算前述计算强度值的可靠度。

试验证明，混凝土质量的形成受诸多因素影响，其中由随机因素导致的质量变化符合正态分布[4]。混凝土材料强度和波速具有良好的相关性，但影响纵向声波在传递过程中会受到很多干扰，这些干扰导致纵向波速的变化规律难以把握。虽然这类随机变量的概率函数很难确定，但如果能取得该随机变量的均值和方差，仍可以用一次二阶矩法近似计算其可靠度[5]。因此，本文对灌注桩桩身计算强度的可靠度采用一次二阶矩法进行了计算。桩身强度可靠度计算过程如下：

对于幂函数模式非线性回归方程：

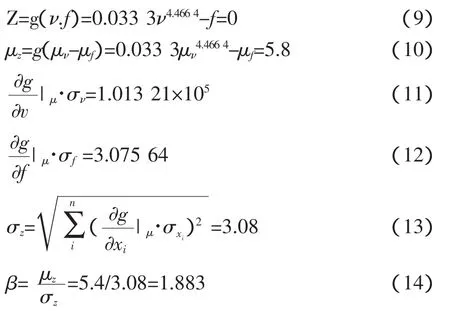
对指数函数模式、抛物线模式和对数函数模式回归方程采用相同的计算方法计算得到：

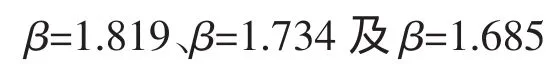
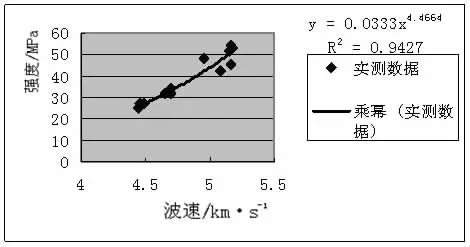
图1 幂函数回归分析曲线Fig.1 Regression curve of power function

图2 指数函数回归分析曲线Fig.2 Regression curve of exponential function

3 灌注桩强度计算值的相对误差分析

利用不同函数模型回归方程求得的桩身计算强度与实测强度值相比存在相对误差，该相对误差的大小能反映出回归方程的准确程度。以现场实测试块抗压强度平均值32.6 MPa为真值，分别计算各回归方程的相对误差，计算结果如表3所示。

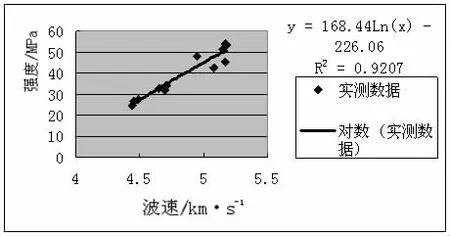
图3 对数函数回归分析曲线Fig.2 Regression curve of logarithmic function

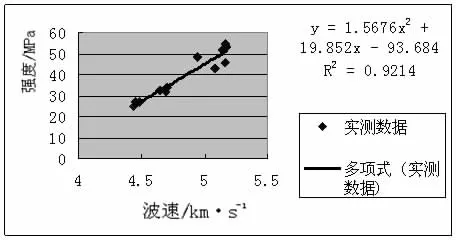
图4 抛物线回归分析曲线Fig.4 Regression curve of parabolic function

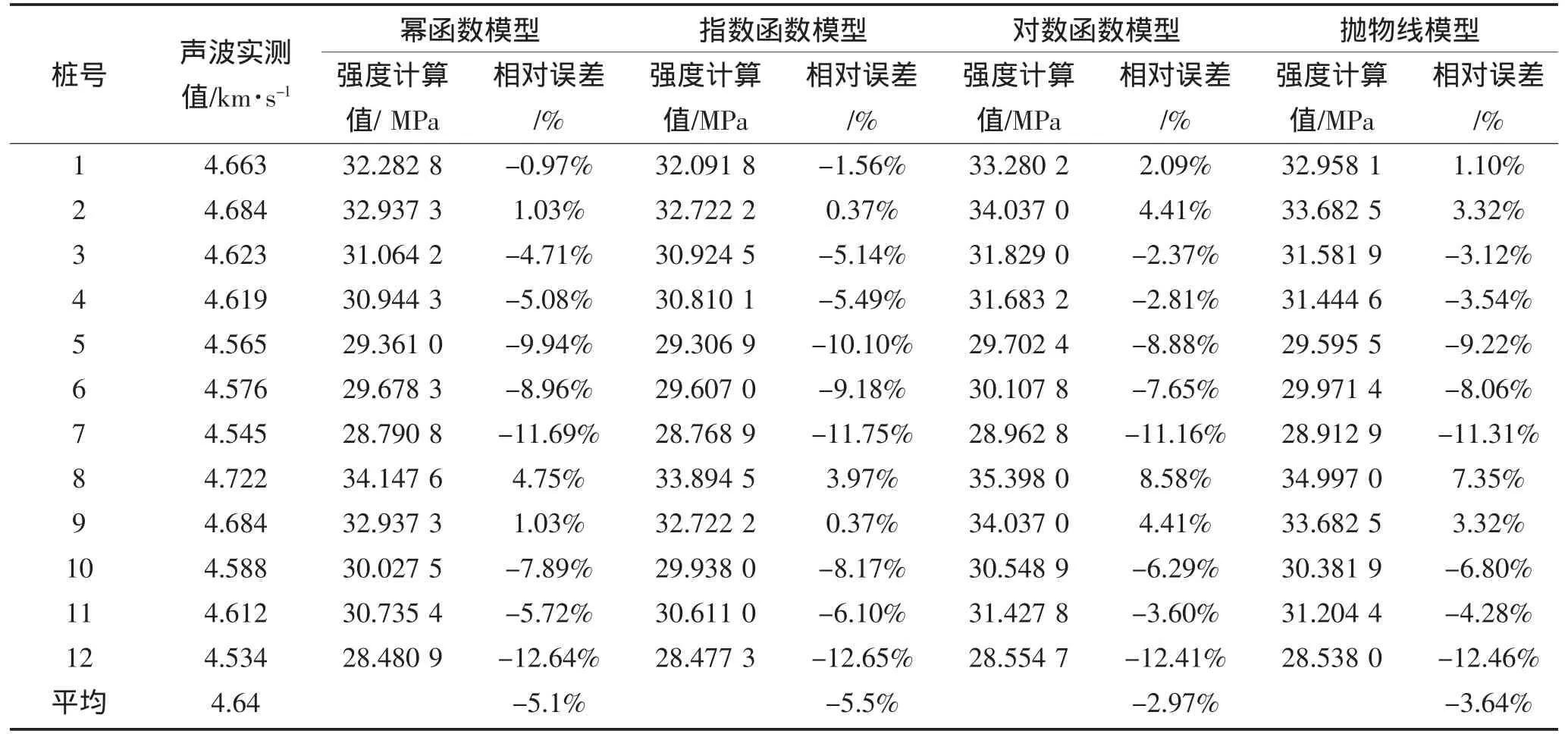
表3 灌注桩强度计算值相对误差Table3 Relative error of calculated strength

由表可知，幂函数模型、指数函数模型、对数函数模型及抛物线模型的回归方程的相对误差平均值分别为-5.1%、-5.5%、-2.97%和-3.64%，平均相对误差值在5%左右，满足工程实践要求。

4 结论

4.1 波速—强度曲线的建立为桩体混凝土质量检测提供了一定的依据和便利，同时为采用超声波测强法检测灌注桩强度提供实践经验。根据本文中的回归方程，利用超声波仪测得的声学参数估算得到具有一定保证率的灌注桩桩身强度，可在工程中用于对灌注桩桩身质量的快速无损检测。

4.2 通过对试验数据的非线性回归分析，建立了幂函数、指数函数、对数函数及抛物线函数4种函数模型的桩身强度计算方程。相对误差分析结果表明，采用回归方程求得的桩身计算强度平均相对误差均在5%左右，满足工程实践要求。但由于影响灌注桩成桩质量的因素很多，桩身强度存在较大波动性，强度计算方程只能对桩身强度做出粗略地估算，需要在实践应用中对方程进行检验和不断完善。

4.3 由前文4个拟合曲线方程可以看到，拟合的幂函数曲线的相关系数最高，达到0.942 7。而拟合曲线方程的可靠度计算的结果分别为1.883、1.819、1.734及1.685，从建筑工程的实际可靠度情况来看，按照四个公式推算灌注桩桩身计算强度的可靠度水平均处于较低的水平。原因有两点：一方面现场灌注桩试块受试块钻取技术及实验室养护条件影响，实测强度波动较大；另一方面灌注桩成桩质量受多种因素影响且桩体工作环境复杂，造成波速测量的准确度受到制约。

[1]王正君，薛文博，张洪祥.灌注桩混凝土超声测强曲线分析[J].低温建筑技术，2008，123（3）:96-97.

[2]邱平.新编混凝土无损检测技术[M].北京:中国环境科学出版社，2002.

[3]张鹏远.超声波透射法检测桩基质量的应用与研究[D].内蒙古：内蒙古农业大学，2011.

[4]陈凡，徐天平，陈久照，等.基桩质量检测技术[M].北京:中国建筑工业出版社，2003.

[5]李清富，高健磊，乐金朝，等.工程结构可靠性原理[M].郑州:黄河水利出版社，1999.