一类双色有向图的极图刻画

罗美金，侯宗毅，乔友付

（河池学院 数学系，广西 宜州 546300）

一类双色有向图的极图刻画

罗美金，侯宗毅，乔友付

（河池学院 数学系，广西 宜州 546300）

考虑一类双色有向图，它的未着色图中含一个m-圈和一个n-圈，且两圈有两条公共弧，给出了本原条件和并对达到指数上界的极图进行了刻画.

双色；有向图；指数；上界；极图

1 引言

设D是一个有向图，如果D是包含红弧和蓝弧的有向图，则称D是一个双色有向图.双色有向图D是强连通的，如果D中每一对顶点(i,j)都存在从i到j的途径.给定D中的一条途径ω，用r(ω)和b(ω)分别表示ω中红弧和蓝弧的条数，称 ω 为一条(r(ω),b(ω))- 途径，ω 的分解为向量 r(ω),b(ω)或(r(ω),b(ω))T.

一个双色有向图D是本原的，当且仅当存在非负整数h和k，且h+k>0，使得D中的每一对顶点(i,j)都存在从i到j的 (h,k)途径，h+k的最小值定义为双色有向图D的本原指数，记为exp(D).

设 C={γ1,γ2,L,γl}是 D 的圈的集合，定义 D 的圈矩阵 M是一个2×l矩阵，它的第i列是γi的分解.M的content(记为content(M))定义为0如果M的秩小于2，否则定义为M的所有非零2阶主子式的最大公因数.

引理1[1]一个至少包含一条红弧和一条蓝弧的双色有向图D是本原的，当且仅当D是强连通的，且content(M)=1.

近几年对本原双色有向图的本原指数的研究已经取得了一些重要成果，见文献[1-7].本文在文献[4]的基础上，做了进一步的研究，研究一类双色有向图D，它的未着色有向图如图1所示.D中仅包含两个圈，圈长分别为m和n，且两圈有两条公共弧，则D的圈矩阵可写为矩阵可写为

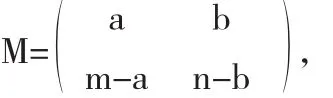
图1 未着色有向图D

2 本原条件及指数上界

定理2 若D是本原的,当且仅当|an-bm|=1.

证明 显然，D是强连通的，则

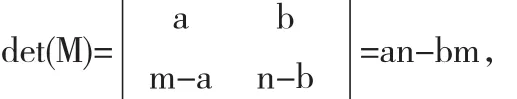
由引理1可得，D是本原的当且仅当content(M)=1，即|M|=±1.定理得证.

下面对D分三种类型讨论：类型1，弧m-2→m-1→m是红的；类型2，弧m-2→-m-1→m是蓝的；类型3，弧m-2→m-1是红的，弧m-1→m是蓝的(或弧m-2→m-1是蓝的，弧m-1→m是红的).

定理3[4]若an-bm=1，D属于类型1，且本原，则

exp(D)≤m(a+b-2)(n-b)+an(m+n-a-b)-2n(m-a)；

定理4[4]若an-bm=-1，D属于类型2，且本原，则

ecp(D)≤bm(m+n-a-b-2)+n(m-a)(a+b)-2am.

定理5[4]若an-bm=1，D属于类型3，且本原，则

exp(D)≤m(n-b)(a+b-1)+an(m+n-a-b-1)-n(m-a)-bm；

3 指数上界的极图刻画

定理6 设双色有向图D是本原的,且an-bm=1，则

exp(D)=m(a+b-2)(n-b)+an(m+n-a-b)-2n(m-a)

当且仅当D中存在一条a+b-2长的红路.

证明 充分性：由定理3，只需证明exp(D)≥m(a+b-2)(n-b)+an(m+n-a-b)-2n(m-a).

设存在一对非负整数(h,k)，使对D中所有顶点对(i,j)，都有一条从i到j的(h,k)-途径.取i=j=m，则存在非负整数u和 v，有

所以，u≥(n-b)(a+b-2).

所以，v≥2(-m+a)+a(m+n-a-b).

=m(a+b-2)(n-b)+an(m+n-a-b)-2n(m-a).

结合定理3,则得exp(D)=m(a+b-2)(n-b)+an(m+n-a-b)-2n(m-a).

必要性:利用反证法.设双色有向图D是本原的,且an-bm=1.若不存在一条a+b-2长的红路,只需证明exp(D)

对D中所有顶点对(i,j)，记pij从i到j的最短路，r(pij)=s,b(pij)=t.只需证明对D的任意一对顶点 (i,j)，都有一条(a(a+b-2)(n-b)-2ab+ab(m+n-a-b)-2b(m-a),(m-a)(a+b-2)(n-b)-2(m-a)b+d(n-b)(m+n-a-b)-2(n-b)(m-a))-途径.取ρ1=(n-b)(a+b-2)-2b-(n-b)s+bt，ρ2=a(m+n-a-b)-2(m-a)+(m-a)s-at.因此，从顶点i出发，沿pij到顶点j，转m-圈ρ1次，转n-圈ρ2次的途径有分解

显然，ρ1≥0,ρ2≥0. 当 s=a+b-2 时,t≥2;t=m+n-a-b 时，s≥2.此时，ρ1=0 或 ρ2=0 时，pij必包含公共弧 m-2→m-1→m.所以,

定理得证.

定理7 若an-bm=-1，D属于类型2，且本原，则

exp(D)=bm(m+n-a-b-2)+n(m-a)(a+b)-2am

当且仅当存在一条m+n-a-b的连续蓝路.

定理8 若an-bm=1，D属于类型3，且本原，则

exp(D)=m(n-b)(a+b-1)+an(m+n-a-b-1)-n(m-a)-bm，

（1）当弧m-2→m-1是红的，弧m-1→m是蓝的时，当且仅当m-a-1→m-a→L→m-1是红的，弧m→m+1→L→m+b是红的，其余弧为蓝的；或，弧m→1→L→a是红的，弧m+n-a-b→m+n-b→L→m+n-3→m-2→m-1 是红的，其余弧为蓝的.

（2）当弧m-2→m-1是蓝的，弧m-1→m是红的时，当且仅当m-a-2→m-a-1→L→m-2是红的，弧m-1→m→L→m+b-1是红的，其余弧为蓝的；或，弧m-1→m→1→L→a-1是红的，弧m+n-2-b→m+n-1-b→L→m+n-3→m-2是红的，其余弧为蓝的.

〔1〕B.L.Shader,S.Suwilo,Exponents ofnonnegative matrix pairs[J].Linear Algebra Appl. 363(2003),275-293.

〔2〕Shao Yanling,Gao Yubin,Liang Sun.Exponentsofa class of two-colored digraphs[J].Linear Algebra and its Applacations.2005,53:175-188.

〔3〕Gao Yubin,Shao Yanling.Exponents of two-colored digraphs with two cycles[J].Linear Algebra and its Applacations.2005,407:263-276.

〔4〕罗美金,侯宗毅,乔友付.一类含有两条公共弧的双色有向图的指数上界 [J].Information Technology and Scientific Management.vo2.(2011):683-687.

〔5〕罗美金,高玉斌.一类含有两个圈的双色有向图本原指数[J].中北大学学报(自然科学版)，2007（5）：377-382.

〔6〕罗美金,高玉斌.一类双色有向图的本原指数[J].中北大学学报(自然科学版)，2008，29（2）:95-100.

〔7〕罗美金,高玉斌.一类恰含三个圈的三色有向图的本原指数[J].山东大学学报(理学版)，2008，43（1）：:65-72.

O157.5

A

1673-260X（2012）06-0008-02

广西自治区教育厅项目(NO.201010LX468)；河池学院科研项目(NO.2010QS-N007,NO.2010A-N004)