基于线性规划的公差综合优化设计方法

许本胜，王 灿，谢云峰

（桂林航天工业学院 机械工程系， 桂林 541004）

0 引言

公差综合，也称公差分配，是在保证装配要求的条件下，确定与之相关各配合零件最优的公差。在产品设计阶段，公差的分配合理与否直接影响到产品的质量及后续过程的加工、使用寿命等。如果设计中规定的公差过小，会加大后续加工的难度及生产成本；反之，如果公差过大，则装配精度降低，影响产品的装配质量。因此，公差的分配成为工程实际中常见的优化问题。

常规的公差综合方法有等公差法、等精度法以及概率法等[1,2]。这些方法主要依靠设计人员根据已有经验，同时参考相关设计手册进行公差分配。由于对设计人员的主观因素和经验依赖程度高，公差的分配容易出现过紧或过松的情况，导致零件加工成本过高或加工完成的零件无法满足装配要求。随着计算机技术的发展，出现了各种计算机辅助的公差综合优化方法。文献[3]提出一种基于加工能力约束最低制造成本的公差优化设计方法。文献[4]以最低制造成本为目标，根据成本与公差间的函数关系，建立了非线性的公差优化模型。文献[5]、[6]以产品最小制造成本为优化目标函数，分别使用遗传算法及粒子群算法进行装配公差的优化分配。这些方法均建立在公差—成本模型基础上，利用各种优化算法进行优化计算。由于加工环境的不断变化，对大量加工工艺数据进行统计分析确定公差—成本模型的参数是十分困难的，因而实际工程中基于公差—成本的优化模型应用非常有限。

针对常规公差综合方法优化不足，以及考虑到实际获取公差—成本关系复杂性的局限，本文将线性规划方法运用于公差综合的优化设计。线性规划方法的一般形式如下：其中X={(x1, x2,!, xn)T| xi∈R,i=1, 2, !, n}为优化变量，A、B、C、D为系数矩阵。

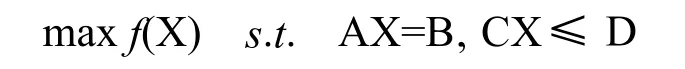
1 尺寸公差综合的线性规划模型

1.1 目标函数

不考虑设计公差与制造成本之间的关系，以所有公差之和最大为优化目标函数，有：

其中ti为第i个尺寸公差；n为公差个数。实际设计中，不仅要给出公差ti的大小，还应给出相应尺寸的极限值，因而本文将上、下极限尺寸作为设计变量，两者差值为设计公差。记公差ti对应基本尺寸为Li，上限、下限尺寸分别为LiU及LiL。式（1）可写为：

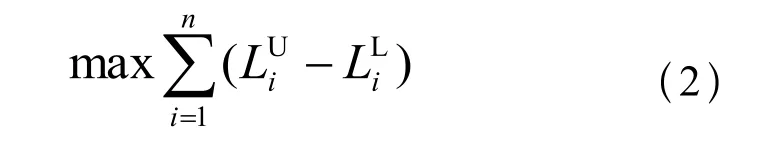
1.2 约束条件

1.2.1 装配要求约束

对于具体的装配要求，以对应装配尺寸为封闭环，从封闭环一端开始搜索，遍历所有与之相关的零件尺寸直至封闭环的另一端，得到与装配要求相关的装配尺寸链。装配尺寸链中零件尺寸为组成环，如果组成环尺寸增大或减小（其他组成环尺寸视为不变）则装配尺寸减小或增大，称两者反向；反之称两者同向。记装配尺寸链中有m个组成环尺寸，DU及DL分别为装配要求对应的最大、最小装配尺寸，得到组成环极限尺寸的装配要求约束如下：

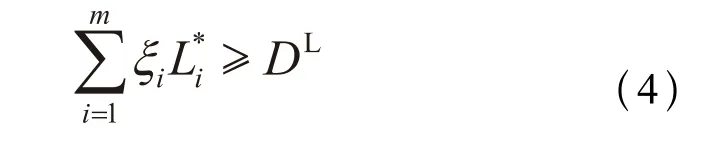
1.2.2 加工能力约束

设计的公差应能够保证实际加工，为此，需要根据实际加工条件确定最小设计公差。加工能力约束可表示为：

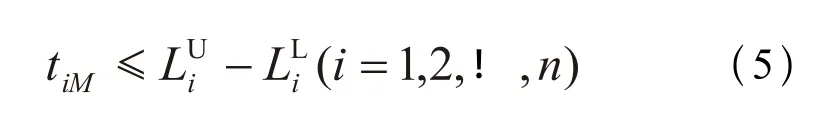
其中tiM为允许最小公差。

1.2.3 初始公差范围

对于尺寸公差较多的情况，式（3）!（5）有时不能够完整约束所有尺寸，考虑设计方法的通用性和稳健性，对各尺寸公差范围进行初步确定，形成式（6）所示的不等式约束。

本文中初始公差范围参考表1确定。

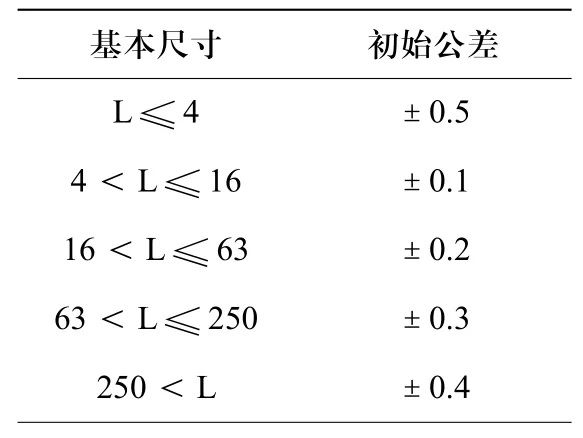
表1 不同尺寸段初始公差范围

2 优化实例

考虑一般情况，装配体中需设计公差数目较多，且往往具有多个装配要求。以图1所示传动轴轴向装配图为例。装配零件主要包括传动轴、左右端盖、衬套、传动齿轮及轴承，其中齿轮及轴承均为标准件，齿轮基本尺寸及偏差为25±0.015，轴承基本尺寸及偏差为7±0.01。其它零件为非标准件，基本及极限尺寸（单位为mm）如图2所示。

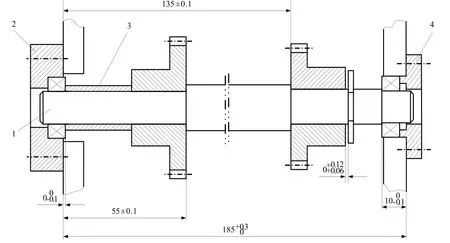
图1 传动轴轴向装配简图

图2 零件轴向极限尺寸

2.1 目标函数

由式（2），确定目标函数如下：

2.2 约束条件

通过图1及图2获得装配要求对应的装配尺寸链，进而确定装配要求约束对应的尺寸链方程。以装配尺寸为例，其装配尺寸链如图3所示。

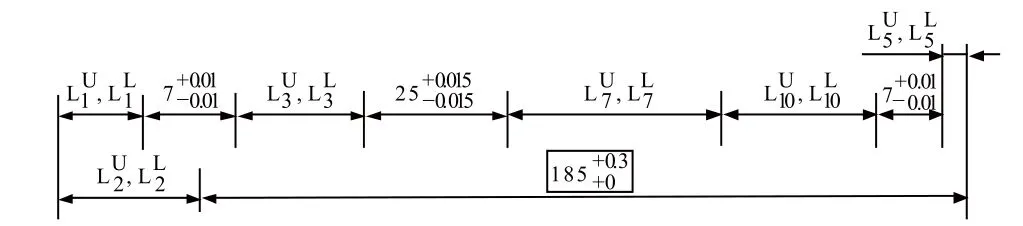
图3 装配要求对应的尺寸链

综合考虑各装配要求，由装配尺寸链可得到以下不等式约束：

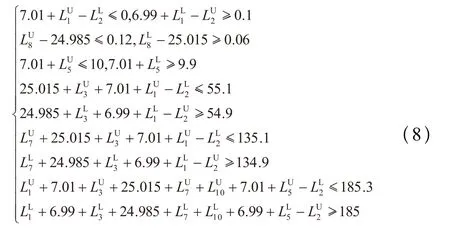
各零件均采用车削加工，通常条件下能够加工保证的最小公差为0.01mm，有：

由图2中各零件轴向基本尺寸结合表1确定初始公差范围如下：

综合式（7）（10）得到图1所示装配体尺寸公差综合的线性规划模型，计算得到各设计尺寸对应的极限尺寸及公差优化结果如表2所示。

3 结论

本文将线性规划方法运用于工程实践中常见的尺寸公差综合优化问题，以设计公差之和最大为优化目标，以产品装配要求、实际加工能力以及不同尺寸段的常见经济合理加工范围为约束条件，研究了尺寸公差综合的优化分配方案。通过实例分析显示了在给定装配功能要求的前提下，线性规划方法能有效生成优化的公差大小以及对应尺寸的极限值，是一种简单实用的公差综合设计方法。

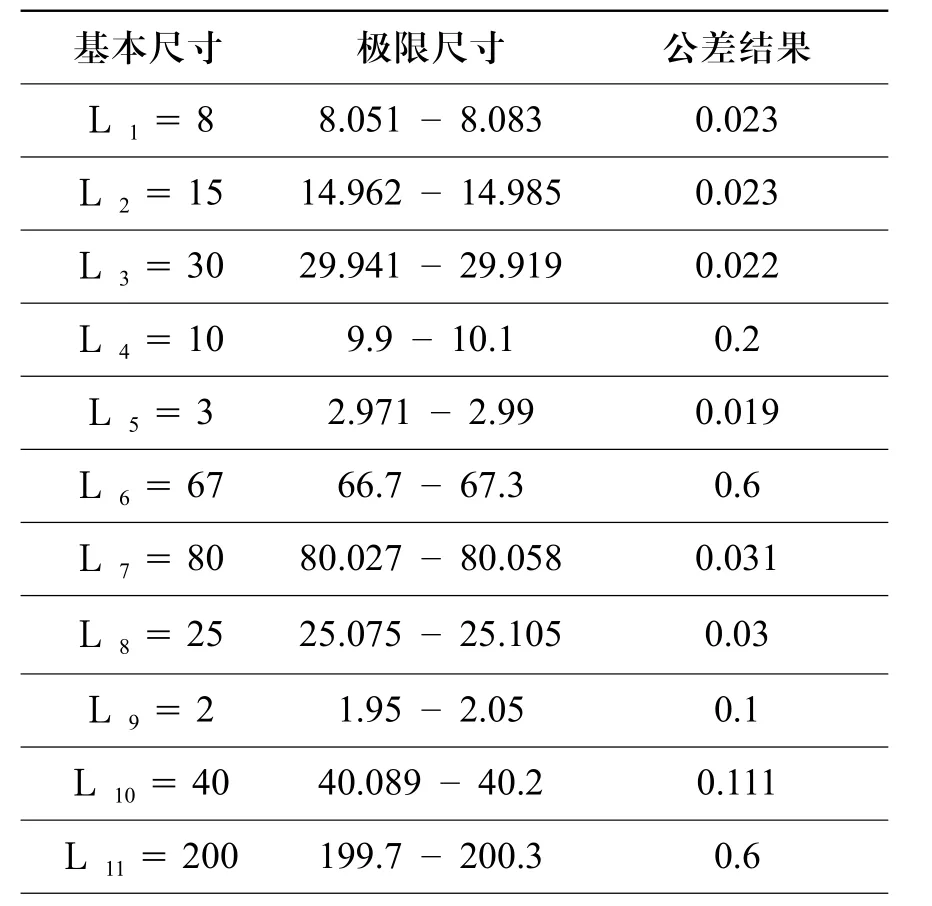
表2 极限尺寸及公差优化计算结果（单位：mm）

[1]吴昭同, 杨将新.计算机辅助公差优化设计[M], 杭州: 浙江大学出版社, 1999.

[2]卢军, 赵丽萍.基于知识的公差设计[J].计算机集成制造系统-CIMS,2001, 7(11): 50-53.

[3]黄美发, 高咏生.基于最低制造成本的一种公差优化设计法[J].华中科技大学学报(自然科学版), 2002, 30(4):19-21.

[4]李淑娟, 李言, 肖继明.基于DFA和DFC的综合公差优化[J].机械科学与技术.2005, 24(2): 143-145.

[5]王伯平, 景大英.基于遗传算法的配合尺寸公差优化设计[J].农业机械学报.2004,35(4):198-200.

[6]匡兵, 黄美发, 钟艳如等.基于粒子群算法的装配公差优化分配[J].机械设计与制造, 2009, 2: 35-37.