噪声对维纳滤波反卷积算法性能影响的分析*
高明哲 祝明波
(1.海军航空工程学院研究生管理大队 烟台 264001)(2.海军航空工程学院电子信息工程系 烟台 264001)
1 引言
扫描体制下的雷达方位回波是由目标方位信息与雷达的天线方向图函数卷积而成,然而通常在远距离处的同一距离单元内,会存在两个或者两个以上的目标,当天线进行扫描时,在接收机处获得的回波信号是多目标方位回波的叠加,如果两个点目标之间的角度间隔小于3dB功率波束宽度,则两个靠近的点目标不能被分辨[1]。雷达方位超分辨是指将处于同一距离单元内的波束宽度内的几个目标区别开来的能力。现代战争对舰用雷达以及弹载雷达对搜索和识别都提出了更高的要求,因此,提高雷达方位分辨力具有重要的实践意义。
维纳滤波反卷积算法是一种简单实用的超分辨算法,近来年,运用维纳滤波反卷积算法实现雷达的方位超分辨受到了越来越多的关注和研究[2~10]。然而雷达在实际搜索过程中所得到的目标回波必定会有噪声叠加,这就对反卷积算法的实际应用效果产生了影响。
本文首先阐述了维纳滤波反卷积的算法理论,其次利用MATLAB对不同信噪比下维纳滤波反卷积算法处理后的雷达回波信号进行了仿真实验,从而得到信噪比对该算法的超分辨倍数的影响,最后对算法的实用性进行评估。
2 算法理论
维纳滤波是利用平稳随机过程的相关特性和频谱特性对混有噪声的信号进行滤波的方法,运用到反卷积问题中可以在最小均方误差下得到真实信号的最佳估计值。基本原理是[11]:
给定观测序列y(n),它是一个非因果系统的输出
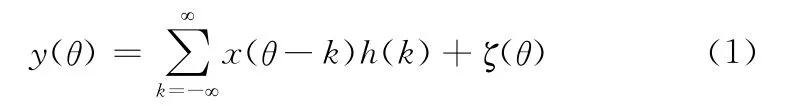
式中,ζ(θ)为噪声。希望找一个非因果滤波器h(θ),它用y(θ)作输入,使其输出:

满足:
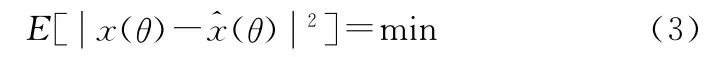
由此得到:

这个式子的离散傅里叶变换给出:

式中,G(ω)是h(θ)的 DTFT。Sxy(ω)和Syy(ω)分别是交叉功率谱和自功率谱。维纳滤波器可以表达为
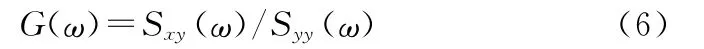
另一方面,由于:
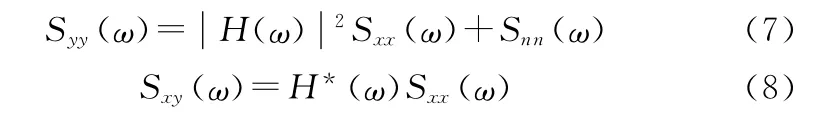
Sxx(ω)和Snn(ω)分别是输入信号和噪声的自功率谱。于是维纳滤波器可以表示为
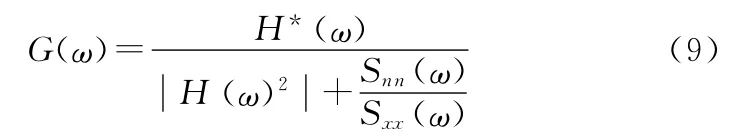
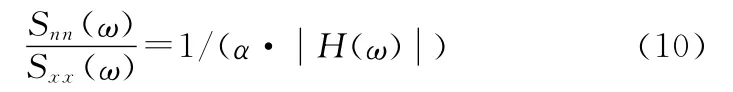
3 仿真分析
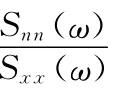

图1 信噪比为60dB时的情形

图2 信噪比为40dB时的情形

图3 信噪比为20dB时的情形
通过仿真对比可以看出,随着信噪比下降,维纳滤波的超分辨性能同样也随之下降,当信噪比降低至20dB时,两目标不可分辨。
通过仿真实验得知,常数α可以对噪声有一定抑制作用,而且对反卷积效果有很大影响。当信噪比较高时,不需要对噪声有很强抑制,α取之较小,也对去卷积的效果影响较小;而当信噪比较低时,α要取较大值来抑制噪声,此时α取值越大,则去卷积效果越差。
调整点目标方位向上的间距,使反卷积的结果刚好能分辨出两个点目标,得到信噪比与维纳滤波超分辨倍数的关系如表1所示。
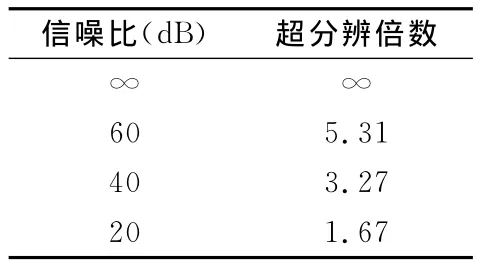
表1 信噪比与维纳滤波超分辨倍数的关系
4 结语
由上面的仿真结果可以看出,随着信噪比的下降,维纳滤波反卷积算法的超分辨倍数也随之下降。在高信噪比时,维纳滤波反卷积算法具有较高的超分辨能力,而信噪比降低至20dB以下时,该算法失去作用。因此我们可以根据噪声环境的不同,选择恰当的信号处理方法,在高信噪比时采用维纳滤波反卷积算法,在低信噪比时采用其他方法,以到达最优的超分辨效果。
[1]丁鹭飞,耿富录.雷达原理[M].第三版.西安:西安电子科技大学出版社,2003:200-201.
[2]Zhao J,Gaydecki PA,Burdekin FM.Investigation of Block Filtering and Deconvolution for the Improvement of Lateral Resolution and Flaw Sizing Accuracy in Ultrasonic Testing[J].Ultrasonics,1995,33(3):187-194.
[3]单荣光,李士国,朱力.去卷积实现雷达方位超分辨[J].船用雷达与对抗,1994(1):9-13.
[4]郭建中,林书玉.超声检测中维纳逆滤波解卷积方法的改进研究[J].应用声学,2005(3):97-102.
[5]李勋,武传华,许士敏.去卷积提高方位分辨率[J].舰船电子工程,2005(5):50-53.
[6]Daly CJ,Rao NAHK.A Spatially Averaged Impulse Response for An Unfocused Piston Transducer[J].J Acoust Soc Am,1999,103(3):1563-1566.
[7]Zhou Daolin,Huang Yulin,Yang Jianyu.Radar Angular Superresolution Algorithm Based on Bayesian Approach[C]//ICSP 2010Proceedings,2010:1894-1897.
[8]Craig E.Morris,Mark A.Richards and Monson H.Hayes.Fast Reconstruction of Linearly Distorted Signals[J].IEEE Transactions on Acoustics,1988,36(7):1017-1025.
[9]Hutchins DA,Pardoe AC,Billson DR.Neural Network Correction of Ultrasonic C-scan Images[J].Ultrasonics,1999,37(4):263-272.
[10]白文斯密,马洪.一种利用多核解卷积提高雷达角分辨力的方法[J].电视技术,2008,12,48(12):43-46.
[11]邹谋炎.反卷积与信号复原[M].北京:国防工业出版社,2001:93-95.

