某型发射装置水平减震系统仿真研究＊

张 强 吴明晨

（1.海军驻郑州地区军事代表室 郑州 450015）（2.郑州机电工程研究所 郑州 450015）

1 引言

某型发射装置水平减震系统由内、外筒和弹、筒间减震装置两级组成，外筒与船体焊接在一起，内筒的上端通过法兰悬挂在外筒上，内筒下端和外筒之间布置一圈筒间减震块；内筒与弹体之间布置4圈适配器，单块适配器通过销子悬挂在弹体外壁上［1］。当发射装置遭受冲击时，减震系统起缓冲、隔振的作用，确保在一定的冲击环境下弹体加速度响应值不能超出规定的要求。文章应用有限元技术建立某型水平减震系统模型，分析发射装置遭受一定程度的冲击后弹体的加速度响应情况。

2 导弹冲击响应过程分析

冲击发生在一个极短时间内。导弹因冲击所产生的运动，可分为两个阶段：冲击作用阶 段，自 由 振 动 阶 段［2］。导弹、适配器、船体构成的冲击系统可简化成如图1所示的力学模型。

当发生基础冲击（因船体运动而产生）时，瞬态的、强烈的冲击波，使适配器产生很大的变形，急剧的能量放大以位能形式最大限度地储存于适配器中［3］，少部分传到弹体上，使弹体受到冲击并产生运动。由于适配器的储能作用，此时弹体产生的加速度较小，冲击完成后，适配器中的能量释放，弹体在初始速度、惯性力作用下开始自由振动。如能量释放得缓慢，且远小于冲击传能的速度，则可以起到缓解冲击的保护作用。如储存的能量被消耗掉，不被用来驱动弹体运动，则具有更佳的缓冲效果。

3 常用的冲击脉冲及谱特性

对船用设备的抗冲击特性进行评价，一般采用试验的方法进行［4］。舰船在战斗条件下可能遭受的冲击环境不能准确确定，为模拟战斗条件下的冲击环境，所有冲击实验均是对设备作用一个脉冲载荷。常用的脉冲载荷有：三角形脉冲，矩形脉冲，指数脉冲，正弦脉冲。

1）三角形脉冲［5］

三角形脉冲具有如下函数形式：

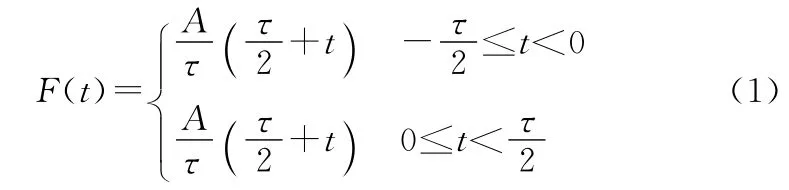
频谱为

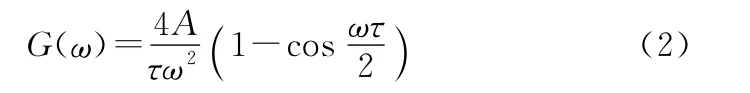
由图2可以看出，三角形脉冲的频谱可覆盖全频段，不是等值谱，能量集中在下述频率点上：

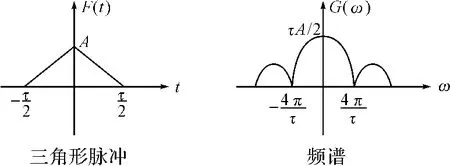
图2 三角形脉冲及频谱

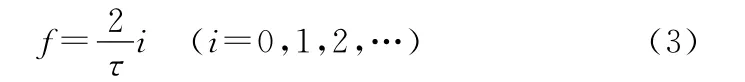
且随着频率的增大，能量衰减。

2）矩形脉冲［5］

矩形单脉冲具有如下函数关系

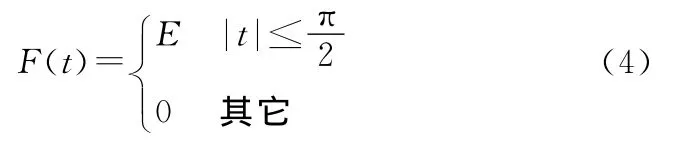
频谱为

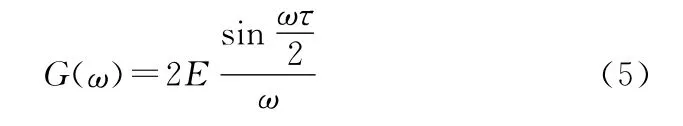
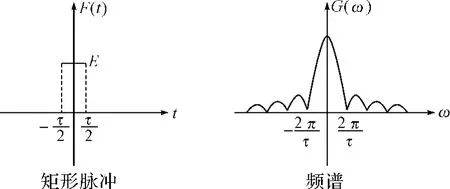
图3 矩形脉冲及频谱

由图3可以看出，矩形脉冲的频谱可覆盖全频段，不是等值谱，能量集中在下述频率点上：

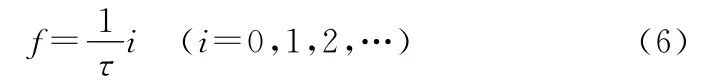
且随着频率的增大，能量迅速衰减。

3）指数脉冲［5］

指数单脉冲具有如下函数关系

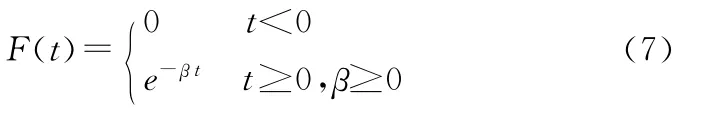
频谱为

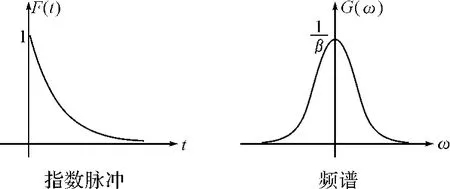
图4 指数脉冲及频谱

由图4可以看出，指数脉冲的频谱可覆盖全频段，不是等值谱，能量随着频率的增大而衰减。

4）简谐脉冲［5］

简谐脉冲具有如下三角函数关系，或正弦脉冲，或余弦脉冲，两者频谱相同：

频谱为

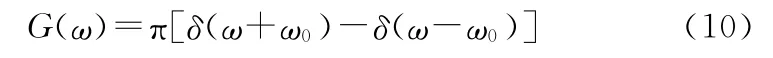
图5 简谐脉冲及频谱

由图5可以看出，正弦脉冲是离散频谱，能量集中在脉冲的频率点处。显然，对结构作用一个简谐脉冲，其谱具有单频特性，能量集中在指定的频率点，所进行的冲击测试验证是单频考核验证。进行一系列的冲击试验，且冲击脉冲频率间隔足够小，即可对整个频段的抗冲击特性进行全面考核验证。

4 仿真计算模型

4.1 弹体仿真模型建立

依据某型的结构参数建立有限元仿真模型，用NASTRAN软件中shell单元［6］模拟壳体结构，在发动机相连处设横隔壁，取发动机在0s时刻的质量作为计算质量，采用等效技术将发动机质量等效到相应的有限元模型上［7］。

4.2 适配器仿真模型建立

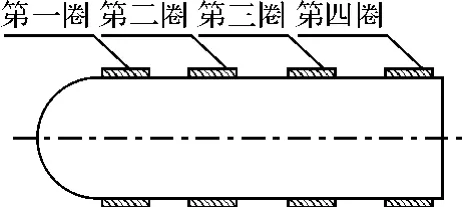
图6 适配器在弹上位置

根据各型适配器的结构特点，将其划分为不同的区域：销钉组件区、预弯柱体区、电缆槽区。再将各个区域划分成若干个子块的集合，每个子块用一个非线性弹性单元模拟［8］，结合整圈适配器的刚度数据定义相应的参数，使模拟后的适配器刚度特性与试验数据一致。非线性弹性单元，选用NASTRAN软件技术的“PBUSH1D”理论［9］。模拟适配器的弹性单元，一端节点在弹体表面，另一端节点在内筒上。适配器位置如图6所示。

4.3 仿真计算模型建立

根据外筒、内筒结构参数建立仿真模型，采用shell、beam单元模拟外筒、内筒结构，采用“点连接”技术模拟内筒与外筒上端的悬挂连接，在内、外筒底部设置一个弹簧单元模拟筒间减震垫，用筒间减震块的刚度特性定义弹簧单元相应的参数。弹体与内筒之间建立模拟适配器的非线性弹性单元，将这些模型组装在一起，即构成减震系统仿真计算模型。

5 仿真计算方法

水下爆炸、碰撞、搁浅、触礁等，对船体和发射装置形成强烈的冲击作用，均可使弹体受到冲击而产生振荡。冲击振荡构成艇上设备的冲击工作环境，通常简称之为冲击环境［10］。本文就10Hz～150Hz频率下的冲击进行仿真计算。对结构作用一个简谐脉冲，其谱具有单频特性，能量集中在指定的频率点，通过进行一系列的冲击试验，即可对整个频段的抗冲击特性进行考核验证，分析弹体遭受冲击后的加速度响应情况。

计算中取冲击脉冲为半正弦波脉冲，每隔20Hz取一个冲击频率点，共取八个频率点构成计算工况。表1是各个频率点工况的横向冲击输入函数。

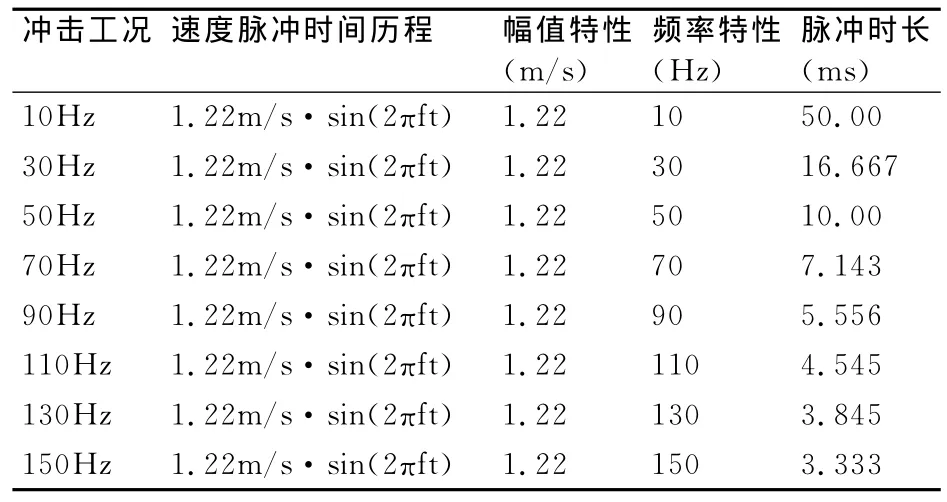
表1 横向冲击输入函数

6 仿真计算结果

通过计算，得出了在不同频率冲击作用下，弹体的加速度响应时间和响应值，结果如图7～14所示。

图7 频率为10Hz的冲击下弹体加度响应

图8 频率为30Hz的冲击下弹体加度响应

图9 频率为50Hz的冲击下弹体加度响应

图10 频率为70Hz的冲击下弹体加度响应

图11 频率为90Hz的冲击下弹体加度响应

图12 频率为110Hz的冲击下弹体加度响应

图13 频率为130Hz的冲击下弹体加度响应

图14 频率为150Hz的冲击下弹体加度响应

通过计算得出了在各频率冲击作用下弹体的加速度时间和响应值，在频率为30Hz、50Hz、70Hz的冲击下弹体加速度响应值偏大。冲击频率超过70Hz后，弹体的加速度响应值越来越小，这说明高频冲击对弹的影响较小。从上图中可以看出，在一次冲击作用后，外筒、内筒的加速度响应值明显高于弹体，这说明水平减震系统具有良好的减震效果。

7 结语

通过仿真计算，弹体在30Hz、50Hz、70Hz的冲击下弹体加速度响应值偏大，冲击频率超过70Hz后，弹体的加速度响应值越来越小，由外筒、筒间减震块、内筒、适配器组成的两级减震系统具有良好的减震效果，能大幅衰减传递到弹体上的冲击。

［1］倪火才.潜地弹道导弹发射装置构造［M］.哈尔滨：哈尔滨工程大学出版社，1998：11－21.

［2］都军民，戴宗妙.冲击响应谱在冲击试验中的应用研究［J］.舰船科学技术，2007：29（1）：1－3.

［3］朱石坚，楼京俊，何其正，等.振动理论与隔振技术［M］.北京：国防工业出版社，2006：160－165.

［4］中华人民共和国国家军用标准.GJB 150.18.军用设备环境试验方法冲击试验［S］.国防科学技术工业委员会，1986.

［5］谢官模.振动力学［M］.北京：国防工业出版社，2007：65－72.

［6］马爱军.PATRAN和NASTRAN有限元专业分析教程［M］.北京：清华大学出版社，2005：35－40.

［7］冷纪桐.有限元技术基础［M］.北京：化学工业出版社，2007：95－98.

［8］殷有泉.非线性有限元基础［M］.北京：北京大学出版社，2007：63－68.

［9］郭已木，万力，黄丹.有限元法与MSC.Nastran软件的工程应用［M］.北京：机械工业出版社，2006：90－95.

［10］中华人民共和国国家军用标准.GJB 1045.3－90.舰艇船体振动评价基准·潜艇［S］.国防科学技术工业委员会，1991.