混合智能算法在需水预测模型中的应用

王 哲，杨学军，柳 林

（海河水利委员会水文局，天津 300170）

传统需水预测方法适用于单一几何增长平稳的序列，并不能反映需水预测中各影响因素之间的动态相互制约关系。20世纪90年代至今，许多学者开始研究支持向量机、人工神经网络等基于数据挖掘、运用计算机智能技术的新方法，这些方法的良好预测性能得到了广泛关注[1]。针对支持向量机模型（Support Vector Machine，简称 SVM）在需水预测中一些关键参数如不敏感损失参数、核参数及惩罚系数等难以确定的问题，提出了运用混合智能算法优化SVM的参数，建立基于混合智能算法的需水预测模型，以减少参数选择的盲目性，提高SVM的预测精度。

1 基于混合智能算法的需水预测模型

1.1 支持向量机

支持向量机通过非线性映射将输入向量从原空间映射到高维空间，在高维空间进行线性回归[2]；同时运用结构风险最小化原则并利用原空间的核函数取代高维空间的点积运算，使复杂的计算得以简化。

最小二乘支持向量机（LS-SVM）将不等式约束替换为等式约束，且将误差平方和损失函数作为训练集的经验损失，简化了计算复杂性，求解速度相对加快[3]。

LS-SVM的核函数包括径向基函数（RBF）、多项式函数、Sigmoid函数等。由于径向基核函数的泛化能力比较强，因此采用径向基核函数，其形式如下：

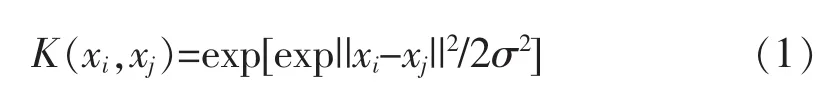
LS-SVM需要确定核参数（σ）和惩罚系数（c），而上述参数的确定缺乏有效参考依据和规则，盲目选择参数降低了模型的预测精度。

1.2 混合智能算法的基本思想

粒子群算法（PSO）有记忆功能，所有粒子都会被保存，而遗传算法（GA）在寻到最优解的同时以前的粒子随着种群的改变而被破坏。PSO是一种单项信息共享机制，仅通过当前搜索到最优点进行信息共享；而GA则在整个种群染色体之间互相共享信息，整个种群较均匀地向最优域移动[4]。因此，基于遗传和粒子群的混合智能算法将粒子群算法与遗传算法相融合，汲取2种算法的优点，克服各自的缺陷，以使其在时间效率上优于遗传算法，在求精确解效率上优于粒子群算法。

混合智能算法的基本思想是利用粒子群算法并行性、记忆能力以及良好的全局寻优能力，避免搜索陷入局部最优，同时借鉴遗传算法中的进化思想，利用杂交、变异算子来进行局部寻优，使其能快速搜索到全局最优点。在搜索解的过程中通过杂交操作加强了对粒子间区域的搜索能力以利用现有而未能合理利用的信息产生更好的解；引入变异操作产生新的解以增加种群的多样性从而减少陷入局部最优的可能性，避免进化过程在早期就陷入局部解而进入终止过程，使之在尽可能大的空间中获得质量较高的优化解。

1.3 基于混合智能算法的LS-SVM参数选取

在LS-SVM求解中，惩罚系数 、核函数及其参数的选择对模型的学习精度和泛化能力的好坏起着决定性作用[5]。

（1）选择核函数：研究和实验表明，RBF是比较好的选择。本文亦采用RBF作为核函数。

（2）惩罚系数（c）：c值较大则允许的误差较小，c值较小则允许较大的误差，c值过大或过小都会使系统的泛化性能变差。一般选择cϵ[0.1 50 000]。

（3）核参数（σ）：控制最终解的复杂性。样本输入范围广，σ取值大；反之，则σ取值小。σ取值太大或太小亦会使系统的泛化性能变差。一般选择σϵ[0.01 100]。

参数c、σ，特别是它们之间的相互影响关系对LS-SVM模型的复杂度、泛化性影响很大[6]。在参数选择时除了对单个参数进行优化还应综合考虑这2个参数形成的参数对，这样逐一的选取方法既费时也不科学。而且选取出的较优解，虽然花费了很多时间，得到的结果也不一定是最优的。为此，笔者采用混合智能算法实现对LS-SVM模型的核参数（σ）和惩罚系数（c）联合优选。

在优选过程中虽然可以任意指定参数训练LSSVM计算训练误差，以此时训练误差为适应值，但是这样容易使模型过度拟合而削弱了模型的泛化能力。最典型的解决方法为使用交互验证技术（Crossvalidation）。适应度函数为求取训练数据集交叉验证MAPE（Mean Absolute Percent Error）的最小值，即：

式中：k为总训练样本子集数，一般取k=5或10；yi为第i个实际值向量；yˆi为预测值向量。

笔者提出的基于混合智能优化算法的需水预测模型，即以最小化训练数据集的交叉验证误差为基础，搜寻最佳化的SVM回归参数值，以期能避开产生过度拟合的风险，提高LS-SVM预测模型的准确度。

1.4 基于混合智能算法的LS-SVM需水预测模型

根据社会经济需水影响因素的分析，可知影响需水量的因素有很多，如人口、经济发展水平、居民生活水平、水价、节水水平、产业结构等。这些因素有一些是不确定的，有一些是随时间变化的。设需水量为因变量，影响因素为自变量，则以下式作为描述需水量预测的数学模型，即：

式中：y 为需水量；x1，x2，…，xm代表的是影响需水量因素。

影响需水量的因素繁多且需水用水影响因素之间关系复杂，因此采用LS-SVM来拟合式（3）。需水量的预测问题转化为由m个影响变量和1个输出量的回归问题。基于混合智能算法优化LS-SVM的需水量预测建模步骤如下：

（1）确定需水量影响因素。将需水量影响因素输入模型，需水量为模型的输出量[7]。将观测数据分成两部分，一部分数据作为训练样本进行参数估计，剩余数据用于预测检验，记输入矢量为X，则：

式中：m为影响需水量的主要因素个数。模型输出为需水量数据 Y=[yi]1×n。

（2）将输入变量、输出变量进行归一化处理。（3）对模型参数c和σ进行优选。

步骤1：初始化。每个粒子由2维参数组成（c，σ），设置群体规模（N）、最大迭代次数（itermax），随机给出初始粒子和粒子初始速度，设定学习因子（c1和c2），给定算法的最大、最小惯性权值因子 （wmax和wmin），变异概率（p0），行为选择概率（p1），模式搜索步长（bc）及误差（eps）。

步骤2：评价种群。以适应度值评价粒子的优劣，粒子的适应度函数值越小，则粒子性能越好[8]。采用粒子个体对应的c和σ，建立支持向量机的学习预测模型，按式（1）计算每个个体的适应值。

步骤3：更新每个粒子的位置和速度。根据行为选择概率（p1），进行交叉操作和模式搜索，并且考虑更新后的速度和位置是否在限定的范围内。

步骤4：判断进化是否停滞。若是，则按变异概率（p0）对粒子群中的粒子进行重新初始化；否则，转入下步。

步骤5：检查结束条件。若比较次数或者精度值满足预设精度，算法收敛，最后1次迭代的最优值即为所求最优值，寻优结束；否则t=t+1，转至步骤2，算法继续迭代。

（4）将最优参数向量（c、σ）赋予 LS-SVM，用样本数据对LS-SVM模型进行训练，得到2个支持向量（a和b）的值。进而预测样本进行预测，通过与实测需水量进行比较，进行模型校验。

（5）最后，用该支持向量机回归模型进行需水量预测。

2 实例研究

将基于混合智能算法优化LS-SVM的需水预测模型运用于秦皇岛市第二产业需水预测过程中，选取与用水量相关性较好、又能衡量需水情况的因子：工业产值、工业规模以上产值、工业规模以下产值、火核电产值、工业水重复利用率、建筑业产值、水价，以2000—2005年调查数据为基础建立基于混合智能算法的支持向量机预测模型，预测2006、2007年秦皇岛市第二产业需水量。

利用模型针对上述学习样本进行秦皇岛市第二产业需水量预测。能否合理确定LS-SVM的惩罚系数（c）和核参数（σ）直接影响到模型的精度和推广能力，笔者通过混合智能算法优化LS-SVM参数对（c，σ）。取群体规模为60，最大进化次数为200，粒子的向量维数为2，PSO加速常数c1=c2=1.5，惯性权重（ω）由 0.9 线性变化到 0.4，选择概率（P1）为0.5，变异概率（P0）为 0.1。 模型计算参数结果，见表1。

通过对参数的搜索，第87代出现了最佳适应值，其值为MAPE=3.669 5。因此，把第87代的最佳个体作为最佳化参数值，此时的参数值分别为c=963、σ=0.274 1，将此参数组合带入预测模型中，对秦皇岛市2006—2007年第二产业用水进行预测。

表1 模型计算参数结果

表2 实际值与预测值对比

图1 模型实际值、拟合值与预测值对比

由表2和图1可以看出，模型计算的拟合值和预测值与秦皇岛市的第二产业实际用水吻合较好。通过统计分析，2000—2005年的拟合部分最大相对误差为0.025 23%，平均相对误差为0.009%；2006—2007年的预测部分，最大相对误差为1.457 82%，平均相对误差为1.373 68%，均小于5%。由此可见，利用该模型预测秦皇岛市第二产业需水发展的结果是令人满意的，具有较高预测精度。

3 结语

（1）基于混合智能算法优化LS-SVM的需水预测模型能够快速地寻优，该方法较单一智能算法具有一定的优越性。

（2）研究实例表明，笔者建立的优化模型能够解决复杂关系的多因素影响因子的需水预测问题，预测模型拟合精度较高，预测结果较合理。

（3）针对预测结果存在误差的问题，在今后的运用过程中需加大样本容量，以便提高预测的准确性。

[1]刘卫林.几种需水量预测模型的比较研究 [J].人民长江，2011，42（13）：19-22.

[2]张伟，吴丹，李小奇，等.基于最小二乘支持向量机的大坝应力预测模型[J].水利与建筑工程学报，2011（1）：26-29.

[3]熊伟丽，徐保国.基于PSO的SVR参数优化选择方法研究 [J].系统仿真学报，2006（9）：22-26.

[4]曹成涛，徐建闽 .基于PSO-SVM的短期交通流预测方法[J].计算机工程与应用，2007（15）：15-18.

[5]梅松，程伟平，刘国华.基于支持向量机的洪水预报模型初探[J].中国农村水利水电， 2005（3）：34-36.

[6]Yu X Y，Liong S Y，Babovic V.EC-SVM approach for realtime hydrologic forecasting[J].Journal of Hydroinformatics，2004，6（3）：209-223.

[7]陈磊，张土乔.基于最小二乘支持向量机的时用水量预测模型[J].哈尔滨工业大学学报（自然科学版），2006，38（9）：1528-1530.

[8]钟伟，董增川，李琪.混合算法优化投影寻踪模型的需水预测研究[J].水电能源科学，2010，28（7）：31-33.