数学建模在高等数学教学中的应用

范媛媛

（滁州学院 数学科学学院，安徽 滁州 239000）

数学建模在高等数学教学中的应用

范媛媛

（滁州学院 数学科学学院，安徽 滁州 239000）

高等数学是理工科大学生必修的一门重要专业基础课程，在高等数学教学中渗透数学建模的思想，可以培养学生的创新意识，提高学生学习高等数学的兴趣.提出了基于案例驱动的课堂教学、积极开展数学课外活动、合理利用数学软件，借助数学实验等措施把数学建模思想融入到高等数学教学的各个环节.

高等数学；数学建模；教学

1 引言

高等数学作为理工科大学生必修的一门重要的专业基础课程，对于培养大学生的理性思维能力和科学处理实际问题的严谨性等方面，具有其它课程都无法取代的作用[1].对于我们每一个讲授高等数学课程的教师来说，在上第一节课的时候，按惯例都会阐述一下课程的重要性，一方面要强调这门课程的基础性作用；另一方面，免不了都要说它在实际中有多么重要的应用价值等等.对大多数学生来说，可能对这门课程在实际中的应用更感兴趣，但是在实际教学过程中，教师却很少真正去解决一些实际问题，理论和实际有些脱节，长期以来，高等数学的教学活动还是以讲授微积分的相关理论和训练学生的计算技巧为主.如果教师能在教学过程中适当融入数学建模的思想方法，在理论讲解的同时注意培养学生应用理论知识处理实际问题的能力，不仅可以纠正部分学生所认为的“高等数学无用”的思想，而且还可以培养学生的创新能力和意识，激发学生学习高等数学的兴趣.

2 数学建模思想融入高等数学教学中的必要性

数学建模就是利用数学理论解决实际问题的一种思想方法，它是将数学理论与实际问题联系起来的桥梁，也就是将实际问题用数学语言来描述和解决.数学建模的人才具有一种特有的能力——“双向翻译能力”，即可以将实际问题简化抽象为数学问题——建立数学模型；然后利用计算机等工具求解数学模型，再将求解结果返回到实际中去，并用来分析解决实际问题[2,3].

大学数学教育的思想核心应该是保证学生掌握理论基础知识的同时，注重培养学生的创新意识和创新能力，提高学生的数学素养和解决实际问题的能力，而数学建模就是实现这一目标的有效途径[4,5].在高等数学教学过程中融入数学建模的思想方法，培养学生将数学知识应用于实际问题和社会实践的意识，加强学生在解决问题的过程中养成的团结合作的精神以及交流、表达的能力.另外，还可以弥补传统数学教学中存在的不足，促进高校数学教师对知识的更新.

3 数学建模思想融入高等数学教学中的具体措施

在培养大学生的创造性思维、意识和能力等方面，数学建模的思想方法具有重要的意义和良好的效果.但在高等数学教学中融入数学建模的思想方法，我们应该注意两个问题:一是教学中必须合理安排教学内容，要以高等数学教学为主，建模过程为辅，以确保高等数学教学任务能够顺利完成；二是教学中要以介绍建模的思想、方法为主，提高建模能力为辅，因为毕竟不是数学建模课程，所以所选实例不宜过于复杂.

3.1 强调数学概念与实际问题的联系

高等数学中许多概念定义的产生都是有其实际背景的，所以应该从实际问题中引入概念，在教学中重视从实际问题中抽象出数学概念的过程，加深学生对数学概念的理解和掌握以及与实际问题的联系.例如：教材中以“ε-N”、“ε-δ”语言给出了数列极限以及函数极限概念的精确描述.但是这种描述对于初学者而言非常地抽象和难以理解，学生只能不加理解地死记硬背，而不能理解其真正的内涵.为了解决这个问题,教学中可从实际问题中引入极限的思想，如我国古代数学家刘徽的割圆术、几何图形按一定规则的变化趋势、一条曲线上点的变化过程等等.在实际问题中给学生展示极限定义的形成过程，让学生理解极限定义的本质，能够轻松掌握利用“ε-N”、“ε-δ”语言证明有关极限问题的解题思路和解题方法.

又比如在讲授导数这个概念时，我们是利用瞬时速度和切线斜率的共性抽象出来的函数变化率给出的导数的定义，但是导数的意义远远超出了斜率和速度的范畴，它渗透到了科学技术的各个领域.教学中可以引导学生发现种群的生长率和死亡率、放射性物质的衰变率、冷却过程的温度变化率、经济学中的边际函数等等与函数变化率有关的实际问题都是与导数的概念有关的.这样学生不仅能够深刻体会到数学概念的实际背景与应用价值,同时也会被导数的巨大魅力所倾倒.

3.2 基于案例驱动的课堂教学

案例驱动是教师根据课堂教学目标和教学内容的需要，通过设置具体案例，引导学生参与分析、讨论、表达等活动，进而提高学生分析问题和解决问题能力的一种教学方式.其本质是理论与实践相结合的互动式教学.与传统教学相比，案例驱动的教学方式显示出理论联系实际，促进学生重视实际应用的优越性.在高等数学的教学活动中，我们可以根据不同的教学内容，选编相应的实际应用问题进行案例教学.

例如定积分的应用其实就是“元素法”的思想，在讲解定积分应用时，我们可以提出这样一个问题：

例1 某城市居民人口分布密度的数学模型是

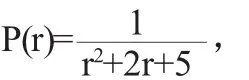
其中r(km)是离开市中心的距离，P(r)的单位是10万人/km2.求在离市中心10km范围内的人口数.(人口分布问题)又如微分方程建模主要用于自然科学（如捕食问题）和社会科学方面（如人口预测、新产品的推广、减肥问题等）的研究.在讲解到微分方程时，我们可以提出这样一个具体问题：

例2 某地区的人口数y与时间t有关，且人口增长率与(N-y)成正比.若初始时刻t=0时的人口数为y0.求人口数与时间t的函数关系？

但是特别要注意的是，我们设计的教学案例应该要遵循以下几条原则：

（1）案例要与教学内容紧密联系，选编的教学案例要能用所学理论知识来解决；

（2）案例最好是学生感兴趣的问题，如经济中的热点问题或生活中的热门话题等；

（3）案例要具有科学性，即所选编的教学案例必须符合实际.

3.3 大力开展数学课外活动,引导学生积极参加数学建模竞赛

大学生数学建模竞赛最早是1985年在美国出现的，1989年北京大学、清华大学和北京理工大学首次组织学生参加美国大学生数学建模竞赛（MCM/ICM），目前全国各理工科院校基本都开设了《数学建模》课程，并组织学生积极参与“全国大学生数学建模竞赛”和MCM/ICM的活动.

大力开展数学课外活动，引导学生积极参加数学建模竞赛是高等数学课程的延续、补充和升华，在活动中可以培养学生的团队精神和互助合作的能力，对于毕业后走上工作岗位有很大的帮助.我们可以采取每个月针对所学的内容开展一次数学建模课外活动，在数学建模活动中，学生可以巩固和加强对课堂教学内容的理解和掌握.而且从某种意义上说，数学建模就是一个小型领域的科研活动，让学生通过此项课外活动更早的接触到科研方法，能够培养学生自觉地应用数学知识、方法去观察、分析、解决生活和科技中的实际问题，全面提高学生的数学素质.而且通过此项课外活动，学生储备了一定的建模知识，为参加数学建模竞赛也打下了基础.

3.4 合理利用数学软件，适当增加上机实验

随着计算机的广泛应用和数学软件的迅速发展，许多复杂的推导都可以利用计算机编程来实现，许多难以用手工画出的图形也可以在计算机屏幕上直观地显示出来，这肯定会对包括高等数学在内的许多课程的教学内容和教学手段产生深刻的影响.在教学过程中我们可以合理地利用数学软件，通过几何直观、数值分析和符号推演三者相结合的方式，促使学生加深对理论知识的理解和掌握，培养学生的应用能力，增强学习效果.

而数学实验强调的是如何培养学生将实际问题和数学理论联系起来，自觉地从一些观察到的现象中归纳数学规律、建立数学模型，并运用数学的方法予以解决，学生在这一过程中一直是参与的主体.这种创造性的学习方法在学生应用数学的意识和创新能力培养方面起到了积极的作用.所以在高等数学的教学中，可以适当增加些上机实验的课时，培养学生的应用能力和创造性思维.

4 结语

总之，在高等数学教学中渗透数学建模的思想方法不仅能够激发大学生学习高等数学的兴趣，体会高等数学的实际实用价值，而且能够培养大学生的辩证逻辑思维、创造性思维以及元认知能力.在教学中融入数学建模思想，在培养和提高学生的想象力、洞察力和创造力的同时，对学生自身综合素质的提升也有着重要的意义和深远的影响.

〔1〕李秀林.高等数学教学中渗透数学建模的探讨[J].吉林省教育学院学报,2009,25(8):40-41.

〔2〕李薇,李卫军,戴明强.将建模思想融入数学教学,培养大学生数学素质[J].湖北师范学院学报,2009,29(3):108-111.

〔3〕林昕茜.数学建模思想在高等数学教学中应用价值的研究[J].桂林电子科技大学学报,2009,29(2):155-158.

〔4〕卢喜森.数学建模思想在高等数学教学中的一个应用[J].广西大学学报(自然科学版),2003,28(10):25-27.

〔5〕原乃冬.高等数学教学中渗透数学建模思想的尝试[J].绥化学院学报,2005,25(4)：134-135.

G642

A

1673-260X（2012）05-0026-02

滁州学院大学数学教学团队建设项目