数学建模教学优秀教学案例解析
——交巡警服务平台的设置与调度
木 仁,白阿拉坦高娃,崔 巍
(1.内蒙古工业大学理学院 数学系,内蒙古 呼和浩特 010051;2.内蒙古大学 数学科学学院,内蒙古 呼和浩特 010021;3.赤峰学院 数学与统计学院,内蒙古 赤峰 024200)
数学建模教学优秀教学案例解析
——交巡警服务平台的设置与调度
木 仁1,2,白阿拉坦高娃3,崔 巍1
(1.内蒙古工业大学理学院 数学系,内蒙古 呼和浩特 010051;2.内蒙古大学 数学科学学院,内蒙古 呼和浩特 010021;3.赤峰学院 数学与统计学院,内蒙古 赤峰 024200)
随着全球经济社会的快速发展,数学建模已经成为了众多学科领域中的焦点问题.各种数学建模方法的推广依然成为了数学建模教学的必要环节.一个优秀的数学建模案例不仅能够真实的反映现实问题同时也能多方面体现数学建模方法.交巡警服务平台的设置与调度问题是一种较为理想的数学建模案例.它不仅能够从多方面体现数学建模方法、培养学生们的创新意识,同时也可以推广到众多实际问题中应用.
Matlab;最短路;线性规划;0-1整数规划;非线性规划;层次分析方法;拟合
1 引言
随着计算机软件功能的拓展,众多复杂的数学建模方法均得到了很好的解决[1].同时也有部分典型案例已经在实践当中得到广泛的应有.然而,由于众多非数学专业学生及非重点院校学生们的数学建模知识的欠缺及计算机应用能力的短板,大部分数学建模方法均未得到很好的推广.在解决实际问题时数学模型的建立及求解同等重要,只懂得其中的一个往往不能很好的解决实际问题.过去的众多数学研究工作者虽然具备了扎实的数学建模理论基础,但由于计算机编程能力的缺乏不能求解出复杂的数学建模问题,而新一代的数学研究工作者虽然具备了一定的编程技巧,但由于数学建模理论知识的欠缺往往不能很好的建立相关模型.这为众多数学建模教学工作者提出了新的挑战.今后,应该怎样推广数学建模教育,提高不同专业学生的创新意识,特别是非数学类专业学生及非重点院校学生们的数学建模能力及求解能力变的尤为重要[2-3].
数学建模所涉领域众多,它不仅能够培养学生们的创新能力,同时也能够为不同学科领域创造出的经济社会价值[4].数学建模方法多样,需要掌握的知识点较多[5].怎样通过数学建模的课程将众多数学建模方法传授给学生们是数学建模教育工作者的所追求的目标[6].对于众多重点院校的学生来说许多数学建模方法都能够较快的接受.然而,对于非数学类专业学生或非重点院校学生而言数学建模方法的传授却是十分困难.特别是随着大范围的扩招,使得非重点院校根本就不能够招收具有扎实数学基础的学生.对于这些学生,应进一步探索传授数学建模方法的方案.其中最为可行的方法就是选择恰当的数学建模案例对不同的数学建模方法进行全方面的解析.这使得数学建模案例的选取变的十分重要.频繁的引进不同案例必然会导致大部分学生在短时间内难以接受相关问题.如果能够通过少数几个案例将众多数学建模方法传授给学生那是最为理想的.
2011年全国大学生数学建模竞赛题目交巡警服务平台的设置与调度题目是一个较为理想的数学建模教学案例.所涉及到的数学建模方法包括Matlab作图,Matlab编程,最短路问题,行遍性问题,计算机模拟,线性规划,非线性规划,层次分析方法,数据的统计分析,数据拟合,综合评价等众多方法.以下对其进行深入的分析讨论.
2 问题的提出
由于警务资源是有限的,如何根据城市的实际情况与需求合理地设置交巡警服务平台、分配各平台的管辖范围、调度警务资源是警务部门面临的一个实际课题.
试就某市设置交巡警服务平台的相关情况,建立数学模型分析研究下面的问题:
(1)附件1中的附图1给出了该市中心城区A的交通网络和现有的20个交巡警服务平台的设置情况示意图,相关的数据信息见附件2.请为各交巡警服务平台分配管辖范围,使其在所管辖的范围内出现突发事件时,尽量能在3分钟内有交巡警(警车的时速为60km/h)到达事发地.
对于重大突发事件,需要调度全区20个交巡警服务平台的警力资源,对进出该区的13条交通要道实现快速全封锁.实际中一个平台的警力最多封锁一个路口,请给出该区交巡警服务平台警力合理的调度方案.
根据现有交巡警服务平台的工作量不均衡和有些地方出警时间过长的实际情况,拟在该区内再增加2至5个平台,请确定需要增加平台的具体个数和位置.
(2)针对全市(主城六区 A,B,C,D,E,F)的具体情况,按照设置交巡警服务平台的原则和任务,分析研究该市现有交巡警服务平台设置方案(参见附件)的合理性.如果有明显不合理,请给出解决方案.
如果该市地点P(第32个节点)处发生了重大刑事案件,在案发3分钟后接到报警,犯罪嫌疑人已驾车逃跑.为了快速搜捕嫌疑犯,请给出调度全市交巡警服务平台警力资源的最佳围堵方案.(具体图及附件参见网站http://www.mcm.edu.cn中的2011年竞赛题目)
3 数学建模教学内容解析
在上一节中提出的问题所涉及数学建模方法较多.本节中将对其进行详细的分析,并指出每一问中可传授的数学建模方法.
数学建模方法传授点之(一)Matlab在数学建模中的应用
Matlab软件因其丰富的工具箱,目前已经成为了数学建模领域最为得心应手的软件[7].同时,由于Matlab在处理数据时与Excel文档,TXT文档及数据库文档等之间的特殊接口,使得数学建模者可以随心所欲的读写和处理各项数据.在处理数据的同时也可将部分内容可视化的显示出来,这使得研究工作者对数据有了更为深层次的认识.在数学建模时不仅需要将众多数据规范化,更需要数据结果的可视化,而在这方面Matlab软件能够较为简便的实现具体的目标.
3.1 数据的可视化显示方法
在题目中给出了各个节点的相关信息. 其中通过各节点的坐标,与该点连接的节点标号及节点是否为交巡警服务平台等信息,可将各区的分布图显示出来.此时,主要通过Matlab中的简单循环语句及作图方法即可画出图形.其中绘制出的A区图形如图1所示.在A区中已有20个交巡警服务平台,图1中的圆圈就是20个交巡警服务平台.整个城区图形及其围堵方案示意图如图2所示.图2中带有箭头的线段指出了围堵交巡警服务平台及出口.
3.2 数据的读写及处理方法
在进行作图时需要将已有数据读到Matlab工作区中使用.具体读取方法有以下三种:
A 直接将Excel数据拷到Matlab中的m文件中,并赋给某一变量;
B 通过Excel的加载宏工具建立Matlab数据与Excel数据之间的相互读取功能;
C 通过Matlab中的xlsread函数将Excel中指定文件读至Matlab工作区.
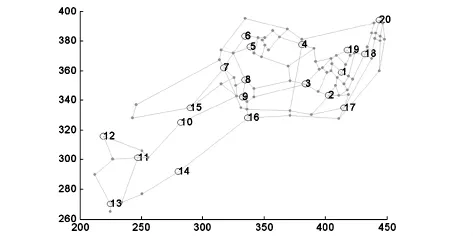
图1 A区的交通网络与平台设置的示意图
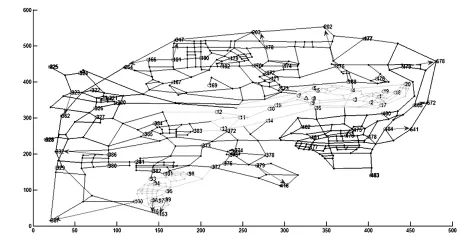
图2 城区的交通网络与平台设置的示意图
3.3 Matlab函数的编写与结果的存储
在计算节点与节点之间的最短路时首先需要计算连接节点之间的距离.通过,Matlab中已经读入的数据及距离函数可计算获得连接节点之间的距离.由于在求解最短路时需要使用该结果,故需保存该数据.具体存储方案有:
A 直接将数据保存为全局变量以便随时进行调用;
B 通过Matlab与Excel之间的接口将其放置到Excel中;
C 通过Matlab中的xlswrite函数将数据写入的Excel中.(低版本的Matlab软件没有写入功能,需要使用Matlab7.0及以上版本)
3.4 利用工具箱求解数学模型
在Matlab工具箱中包含了众多数学建模现成软件.其中常用且较容易使学生们学会的数学建模软件主要有:
A 线性规划Matlab求解函数linprog:线性规划理论[8]在数学领域基本趋向于完备化的阶段.然而,线性规划在实践当中的应用仍然没有得到普及.主要原因在于懂得线性规划的研究工作者基本都是科研工作者.很少有研究工作者将其投入到实践当中应用.而相反需要用到线性规划的人并不知道线性规划能够为其带来的经济社会价值或根本不可能学会线性规划模型更不用说线性规划模型的求解了.
随着经济社会的发展,落后或发展中国家必然将会从劳动密集型转化为技术进步型.而技术的进步离不开数学建模众多方法.其中较易普及的便是线性规划.毫不夸张的说现如今能够通过软件能够解决复杂决策问题或不同类型决策问题的人过于缺乏,其中包括众多教师.那么这一理论及实践的推广就可想而知了.从而今后的数学教育特别是非重点院校应该更加重视学生们的理论与实践的结合及简单理论的深层次推广.而不是漫无目的的传授多种复杂的理论.但部分教师特别是学基础数学出身的教师过于迷醉与自己所学领域的探索,而并未考虑到在当今时代本可以盛行的优秀数学理论及其求解方法的推广.这也在部分程度上体现了作为大学数学老师所缺乏的各学科全面发展的能力.
B 整数规划Matlab求解函数:在实践当中整数规划的使用率也不比线性规划差多少.其中对于大部分决策问题0-1规划可能更具实用性.本文中提出的题目即是一个典型的例子.这一例子还可以进一步推广到管理中心的选择问题等众多问题.
在Matlab中0-1整数规划的求解函数为bintprog.对于普通类型的整数规划可通过线性规划函数的四舍五入的方法获取.对于不满足约束条件的特殊情况可进一步对变量进行约束的方法获取较优的可行解.
lingo软件当中可直接通过变量的整数约束获取整数规划问题的最优解.但lingo软件的数据读取及处理功能远不及Matlab软件.
C 非线性规划的Matlab求解:在Matlab中提供了无约束优化问题的求解算法.而由于非线性规划问题可通过引进辅助函数将其转化为无约束最优化问题.
D 微分方程的Matlab求解:在Matlab中不仅可以对微分方程进行数值计算,同时也提供了微分方程的符号计算方法.
E 数据的统计描述、分析及模拟方法.
F 回归、插值与拟合.
数学建模方法传授点之(二)最短路问题及行遍性问题
为了给各个交巡警服务平台分配管辖范围,需要计算各个节点之间的最短距离.由于已经得知了与每个节点连接的节点标号及连接节点之间的距离,故根据Dijkstra算法可获得某一顶点至各个节点的最短距离的同时也可通过Floyd算法获得每个节点之间的最短距离.算法的具体思想及方法参见参考文献[5].
交巡警不仅需要对管辖范围内的案件进行快速的处理,同时为了避免案件的发生也需要对管辖范围内进行定期的巡逻,而这一问题正是数学建模方法中的行遍性问题.
目前随着网购热潮的兴起,大部分快递公司急需懂得快件的投放及管理的人才.在这一过程中管理者必需懂得最短路问题及行遍性问题方能更加全面快捷的投递快件.因此将部分数学专业学生培养为该方面的人才是一个较好的出路.
数学建模方法传授点之(三)线性规划问题
在不考虑交巡警服务平台的工作量的前提下,各个交巡警服务平台分配管辖范围的确定问题归结为每个节点与服务平台之间的距离的最小化问题.在得知各个节点之间的最短距离的前提下只需通过Matlab循环语句就可以通过逐个比对分配管辖方法.
除了上述分配管辖范围的方法之外,还可以0-1建立线性规划模型对其进行求解.由于为各个交巡警服务平台分配管辖范围,使其在所管辖的范围内出现突发事件时,尽量能在三分钟内有交巡警到达事发地,这一问题等价于为各个交巡警服务平台分配管辖范围,使得从交巡警服务平台到各个节点的距离总合最短的问题.从而,可建立如下0-1整数规划模型:

上式中xij表示第j个节点是否属于第i个交巡警服务平台的管辖范围,如果属于则xij=1,否则xij=0.约束条件表示第j个节点必须属于某一交巡警平台管辖范围.dij表示第i个节点到第j个节点的最短距离.
对于重大突发事件,需要调度全区20个交巡警服务平台的警力资源,对进出该区的13条交通要道实现快速全封锁.实际中一个平台的警力最多封锁一个路口,请给出该区交巡警服务平台警力合理的调度方案.该问题转化为在20个交巡警服务平台中选出13个交巡警服务平台,使得该13个服务平台到13条交通要道之间的距离总合最短.从而针对这一问题建立如下0-1规划模型
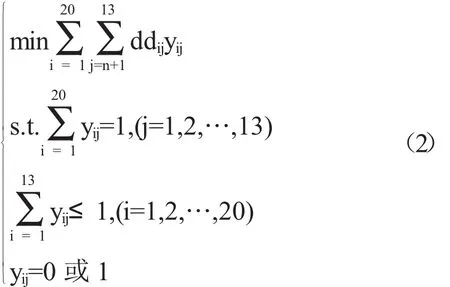
上式中ddij表示城区A中第i个交巡警服务平台到第j条交通要道的出口节点之间最短距离.约束条件表示第j个出口必须由某一交巡警服务平台所封锁;表示第i个交巡警服务平台至多封锁一个出口.
同理如果该市地点P(第32个节点)处发生了重大刑事案件,在案发3分钟后接到报警,犯罪嫌疑人已驾车逃跑.为了快速搜捕嫌疑犯,需给出调度全市交巡警服务平台警力资源的最佳围堵方案.该问题等价于80个交巡警服务平台对17个出口的围堵问题,为了尽快进行围堵,需要让围堵时所行使的路线长度总和最小化,从而可建立出如下0-1规划模型:

上式中dddij表示第i个交巡警服务平台至第j个出口的最短距离,ddddj表示第32节点至第j个出口的最短距离.约束条件dddijzij+3000≤ddddj表示第i个交巡警服务平台如果封锁第j个出口,则第i个交巡警服务平台到第j个出口之间的距离再加上3分钟的行驶时间3000m后的距离要小于等于案发现场到第j个出口的距离.其它约束条件的解释与(2)式类似.
上述三个0-1整数规划模型并不复杂. 但由于数据量较大,很难通过人工输入系数矩阵.因此,必需借助计算机工具计算出各个最短距离,然后通过算法生成各个系数矩阵.其中存在着大量的稀疏矩阵,通过循环语句可以较快生成.
如果利用Lingo等线性规划软件进行求解,不仅在数据的读写方面存在较多问题,且随着变量个数的提高短时间内难以计算获得最终结果.
数学建模方法传授点之(四)非线性规划问题通过模型(1)分配出来的各个交巡警服务平台的工作量并不均衡,每个交巡警服务平台的总发案率为
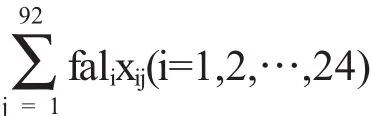
为使各个交巡警服务平台的工作量均衡,需要调整各个交巡警服务平台所管辖的节点或节点个数,使得每一个服务平台的案发率尽量接近发案率平均值,即与发案率平均值之间的差距总和最小化,同时必须满足与交巡警服务平台之间的距离小于3000m(即3分钟内能够到达案发现场),从而建立如下模型:

该模型等价于

上述模型为二次规划模型,通过Matlab中的quadprog函数加以求解,但quadprog函数只能求解一般情形下的二次规划,不能求解决策变量为0-1的二次规划.因此模型(4)和模型(5)还需要寻求相关非线性规划理论求解方法[9].
数学建模方法传授点之(五)数学模型的可行求解方法
由于模型(5)是一个0-1二次规划模型,因此当变量的个数相对较少时完全可以通过穷举法及神经网络方法加以求解.
由于通过最短距离容易得知与交巡警服务平台距离小于3000m的所有节点.从而模型(5)可利用人工分配的方法加以求解.但该方法只能近似获得最优解.
在求解模型(5)时可获得每个节点的最优分配方案(将节点分配给距离最近的交巡警服务平台).但这必然会让部分交巡警服务平台的工作量过高或过低.此时,可设定每个交巡警服务平台工作量的上线,然后逐一将各个节点分配出去.在分配过程中可根据最优分配方案及次优分配方案的差距分配各个节点.
数学建模方法传授点之(六)层次分析方法
在评价交巡警服务平台设置的合理性时,决策者需要考虑众多因素.不同因素在不同程度上影响着交巡警服务平台设置的合理性.同时每一个因素又受到相应子因素的影响.在确定各个指标权重时需要利用层次分析方法来确定.
利用Matlab不仅可以较简单的计算出各个特征值及特征向量,同时还可以用较简单的算法确定各个指标的权重.相对其它众多软件Matlab是一个较好的层次分析方法权重确定软件.
数学建模方法传授点之(七)拟合
在确定交巡警服务平台平均应承担的报警次数时需要考虑城区面积、城区人口及单位面积人口数量之间的关系.城区面积相对稳定,但城区面积将随着城市的经济社会发生改变.从而需要通过以往数据计算拟合[10]出交巡警服务平台平均应承担的报警次数与城区面积、城区人口及单位面积人口数量之间的关系.
4 结论
全国大学生数学建模竞赛已经成功举办了20年.在这二十年期间数学建模虽然得到了一定的推广,但数学建模的教学工作有待提高.特别是对非重点院校及非数学专业学生数学建模的教学工作更需加强.数学建模的教学工作的提高应优先从教师做起.只有教师的数学建模能力提高的一定水平才能够推动数学建模教育.而一个优秀的数学建模实例,必将为教师及学生们的数学建模能力的提高起到至关重要的作用.交巡警服务平台的设置问题是一个较好的数学建模实例.且该题目可以进一步推广到厂址的选择问题,管理中心的确定问题等众多热点问题中.
〔1〕姜启源.数学模型[M].北京:高等教育出版社,1997.
〔2〕叶其孝.数学建模教学活动与大学生教育改革[J].数学实践与认识,1997,27(1):92~94.
〔3〕王茂芝,郭科,徐文皙,周游.数学建模中的创新意识培养[J].大学数学,2009,25(1):126~129.
〔4〕李尚志.培养学生创新素质的探索——从数学建模到数学实验[J].大学数学,2003,19(1):46~50.
〔5〕赵静,但琦.数学建模与数学实验[M].北京:高等教育出版社,2008.
〔6〕李炳照,王宏州,孙华飞,陈一宏.数学建模思想融入数学类课程的思考与实践[J].高等理科教育,2006(5).
〔7〕罗建军,杨琦.Matlab 教程[M].北京:电子工业出版社,2006.
〔8〕何坚勇.运筹学基础[M].北京:清华大学出版社,2008.
〔9〕袁亚湘,孙文瑜.最优化理论与方法[M].北京:科学出版社,2006.
〔10〕盛骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2008.
O29
A
1673-260X(2012)05-0017-05
内蒙古自治区自然科学基金项目(批准号:2011MS1002);内蒙古大学“211工程”创新人才培养项目资助

