海运石脑油储罐水相区阴极保护电场的数值模拟
齐建涛, 李 焰
(1.中国石油大学(华东)化学工程学院, 山东 青岛 266580; 2. 中国石油大学(华东)机电工程学院, 山东 青岛 266580)
石脑油储罐罐底处于腐蚀性较强的沉积水的腐蚀环境中, 通常采用阴极保护方法来对其腐蚀加以控制。然而, 由于传统的阴极保护设计方案没有考虑保护电流密度在空间上的不均匀性和随时间的变化,往往造成设计方案不尽合理, 易导致保护不足或者过保护现象[1-2]。此外, 使用较大的安全因子往往也造成阴极保护系统的经济性降低。
在过去很长一段时间内, 对阴极保护电场的精确计算由于受到实际工程问题中非线性边界条件的影响, 导致问题的解析解无法得到。然而, 近十几年随着计算方法和计算机技术的飞速发展, 使得采用数值计算的方法来处理工程问题的非线性边界[3-5],获取阴极保护电场的高度精确的数值解成为现实[6-7],并且在阴极保护电位计算[8-10]、阴极保护优化[11-12]、腐蚀电磁场计算[13-14]等领域得到广泛应用。与传统的经验设计方法相比, 数值模拟具有在设计阶段就可预测所设计的牺牲阳极系统的保护效果、牺牲阳极数量和位置更精确、阴极保护电位分布均匀、过保护和欠保护现象改善等优点。因此, 采用数值模拟的方法来解决防腐问题已经成为当前阴极保护研究的一个重要方向[15]。
本文采用边界元方法针对海运石脑油储罐罐底水相区的阴极保护设计进行了数值模拟, 并通过对原方案的优化改善了罐底过保护现象。
1 边界元法仿真的基本原理
稳态阴极保护电场的控制方程为:

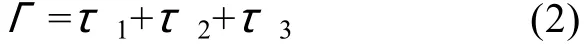
式中:k, 电解质的电导率;V, 电位;Γ, 水相区Ω的边界;τ1, 阳极表面;τ2, 绝缘面;τ3, 被保护的阴极表面。
具体而言, 水相区边界条件如下:
阳极表面τ1和阴极表面τ3满足各自极化曲线:

而绝缘面τ2满足法线方向电流密度为0:

式中:I是电流密度(mA/m2),E是电位(V),n是外法线方向;f是极化曲线满足的函数关系。
由格林公式得与式(1)对应的边界积分方程:
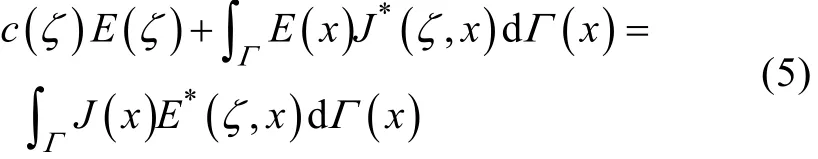
式中:c(ζ) 为系数, 只依赖于物理模型中边界的几何形状;E*(ζ,x)和J*(ζ,x) 为拉普拉斯方程电位和电流密度基本解。对于三维问题:

将边界Γ划分为n个单元后, 式(6)可表示为:

定义:

式中:ijδ为狄拉克函数。由式(7)可得:

通过求解式(8)即可获得研究对象表面电位和电流密度分布[16]。
2 数值仿真结果
2.1 阴极保护系统设计方案
以某石化企业5 000 m3的海运石脑油储罐为例进行设计。储罐主体钢板材料为Q235-A, 内直径为23.76 m, 水相区高度取为1.5 m[17], 罐底积水成分接近海水, 可按海水近似处理, 对由罐底和距罐底1.5 m的侧壁组成的水相区进行设计计算。阴极保护系统的设计保护寿命为10年。
本文按裸钢和涂层联合保护等两种方案分别进行设计。阳极选用A-12-C-2型铝-锌-铟-锡合金牺牲阳极, 尺寸参数详见文献[18]; 储罐内壁涂料选用100%全固态聚氨酯防腐涂料或改性环氧树脂防腐涂料。基于平均电流密度的设计思想[19], 裸钢条件下采用 80 mA/m2的保护电流密度, 安全系数取 1.1,罐底中心安装牺牲阳极1块, 其余按半径2.5、4.5、6.5、8.5和10.5 m对称、均匀地安装5、9、14、20和 50块牺牲阳极, 数量合计为 99块(图1); 涂层联合保护时采用 20 mA/m2的保护电流密度, 安全系数取1.1, 阳极按半径5和10 m对称、均匀地安装7和14块牺牲阳极, 数量合计为21块(图2)。施加阴极保护的储油罐, 其阴极保护区间为–850~–1 100 mV(相对铜/硫酸铜参比电极)[19], 但为避免电位过负导致罐底板焊缝区发生氢脆或导致涂层阴极剥落等不利影响的发生, 一般要求最负的阴极保护电位不超过–1 050 mV, 即–850~–1 050 mV 是合理的阴极保护区间。如牺牲阳极安装位置距浮盘支腿较近, 可做适当调整, 避开支腿位置。
2.2 建模和边界条件
2.2.1 数学建模
石脑油储罐阴极保护电场仿真和优化属于有限域(内域)问题, 本文采用三角形线性单元对罐底水相区的边界进行网格划分。
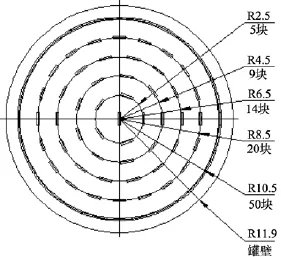
图1 裸钢的保护方案Fig. 1 Protection design for naked steel

图2 涂层加牺牲阳极的保护方案Fig. 2 Protection design for painted steel
2.2.2 边界条件
(1)计算介质按海水处理, 电导率为4.0 S/m。
(2)罐底水相区边界。储罐罐底和侧壁的材料都是 Q235-A, 电流密度和电位满足其阴极极化曲线;而牺牲阳极为Al-Zn-In-Sn阳极, 电流密度和电位满足其阳极极化曲线, 此处略去。
(3)油水分界面处理为理想绝缘边界, 即法向电流密度为0。
2.2.3 数值计算及后处理
本文采用自编边界元程序实现(8)式的求解, 数据经后处理图形软件绘制而成。
2.3 计算结果与讨论
2.3.1 裸钢条件下的牺牲阳极保护
由图 3中的电位云图可以看出, 水相区的电位范围是–995~–1 080 mV。保护电位的变动范围大, 说明水相区电位分布很不均匀。其中, 侧壁电位在–1 010 mV左右, 电位变动有30 mV, 保护良好; 但是在罐底板最外侧电位均低于–1 050 mV, 而且连接成带状, 属于严重过保护区域。从图4中也发现这些区域电流密度超过 300 mA/m2, 很可能存在较大的析氢电流。值得一提的是, 过保护区靠近罐底和侧壁的焊接区, 析氢反应的存在容易导致焊缝的氢致开裂。因此, 对过保护区阳极数量应适量减少, 并重新布置, 以缩小阳极附近过保护区域面积, 并避免其相互叠加, 减少过保护带来的危害。
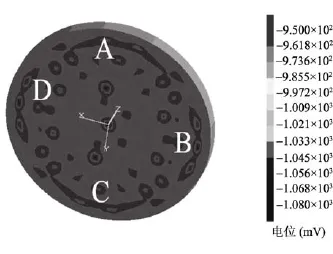
图3 电位云图Fig. 3 Potential plot

图4 电流密度云图Fig. 4 Current density plot
2.3.2 涂层加牺牲阳极的联合保护
在图5所示的电位云图中, 电位范围是–1 027~–1 080 mV, 电位范围相对较窄, 说明整体电位分布较为均匀。具体而言, 侧壁电位在–1 030mV左右, 且变动范围有 10 mV, 说明侧壁保护效果良好; 而在罐底板上可见电位值在–1 035 mV左右且分布均匀,但也存在不少过保护区域, 主要集中于牺牲阳极附近, 过保护面积近总面积5%。其中最外层和内层等处最为明显, 电位值低于–1 050 mV, 电流密度超过100 mA/m2, 如图6所示。对于过保护区的阳极可以适当减少数量, 并在罐底重新布置。
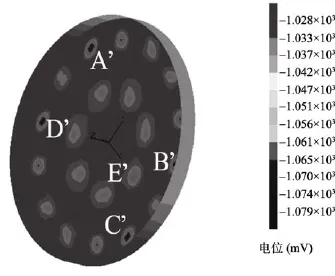
图5 电位云图Fig. 5 Potential plot
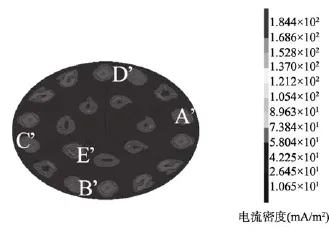
图6 电流密度云图Fig. 6 Current density plot
2.3.3 优化方案
将裸钢条件下阴极保护设计中最外层(R=10.5 m)阳极数量从50块减少为40块, 次外层(R=8.5 m)阳极数量减少为 19块, 并且均匀、对称布置, 其余保持不变, 可获图7所示优化方案。
将涂层联合保护条件下阴极保护设计中最外层(R=10 m)阳极数量从14块减少为10块, 内层(R=5 m)阳极数量从7块减少为6块, 并在罐底均匀、对称布置, 可获图8所示优化方案。

图7 裸钢的牺牲阳极保护优化方案Fig. 7 Optimal design of sacrificial anode protection for the naked steal tank
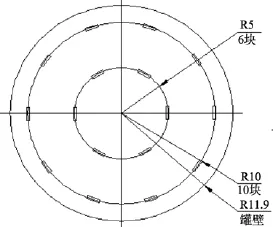
图8 涂层加牺牲阳极保护方案Fig. 8 Optimal design of sacrificial anode protection for the painted steel tank
2.4 优化结果和讨论
2.4.1 裸钢的阴极保护系统优化
图9与图 3比较可以明显发现, 电位范围为–966~–1 081 mV, 仍然较宽且电位梯度较大, 表明电位整体分布不均匀。但是由于外层阳极数量的减少, 侧壁电位在–990 mV左右, 正移了将近 20 mV,而侧壁电位变动范围仅有 20个 mV, 说明侧壁的保护效果更好了; 同时, 在罐底板上过保护现象(尤其是最外层和次外层)得到了明显改善: 过保护区(低于–1.050 V)仅在个别牺牲阳极附近出现, 且零散分布; 对照图 10可知, 原来过保护现象严重的最外侧牺牲阳极的电流密度在92 mA/m2以下。这说明通过调整外层阳极数量和布设位置来进行方案优化的思路是正确的。不过, 由于只是对外层阳极进行处理,对比图9和图5可以发现内层过保护现象没有改善。因此, 进一步减少内层阳极数量并重新布置, 将取得更为理想的保护效果, 后续工作也证明了这一点,此处省略。
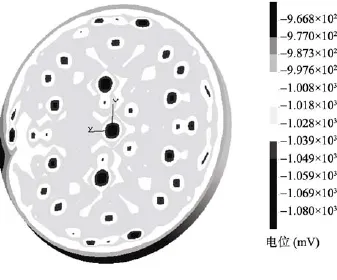
图9 优化后电位分布Fig. 9 Optimal potential distribution

图10 优化后电流密度分布Fig. 10 Optimal current density distribution
2.4.2 涂层加牺牲阳极保护系统优化
由图 11可见, 经优化后的罐底电位范围是–1 013~–1 060 mV, 电位范围很窄, 整体电位分布更均匀。具体而言, 虽然侧壁整体电位变化只有不到10 mV, 但是在外层阳极之间的侧壁上电位梯度变化较大; 而在罐底板上, 外层阳极附近电位均在–1 030 mV左右, 电流密度在60 mA/m2左右。如图12所示, 罐底水相区的过保护现象得到明显改善。然而, 内层6块阳极附近有过保护迹象, 电流密度接近120 mA/m2。这说明仅通过调整外层阳极数量和布设位置来进行方案优化是存在局限的, 而进一步减少内层和外层阳极数量并重新布置, 将取得更为理想的保护效果, 后续工作也证明了这一点, 此处省略; 文献[10]和[12]同样也是通过减少过保护区阳极数量和重新布设阳极的方法, 使得舰艇和压载舱表面电位达到保护区间, 且分布更为均匀。以上工作说明, 数值模拟和优化具有很高的可靠性、实用性和经济性。
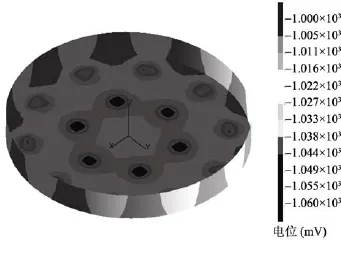
图11 优化后电位分布Fig. 11 Optimal potential distribution

图12 优化后电流密度分布Fig. 12 Optimal current density distribution
3 结论
基于平均电流密度的阴极保护设计往往选取偏大的安全系数, 导致采用的阳极数目过多, 易出现过保护现象。而利用边界元方法进行数值模拟和仿真, 可以对传统的设计方案进行有效、合理的优化,提高其可靠性和经济性。本文在数值模拟的基础上通过适当减少过保护区阳极的数目和调整阳极的位置, 可以明显减少过保护现象, 且罐底水相区电位和电流密度的分布也更为均匀, 取得了较为理想的效果。此外, 优化方案数值模拟结果表明仅仅针对特定过保护区阳极调整是不尽如人意的, 应通盘考虑不同阳极之间相互影响, 合理优化阳极数目和位置,才能取得最佳的保护方案。
致谢: 本文完成过程中得到中船重工第七二五研究所“海洋腐蚀与防护”国防重点实验室的邢少华工程师的帮助,在此予以诚挚的感谢。
[1]贝克曼. 阴极保护手册(原著第三版)[M]. 胡士信,王向农, 译.北京: 化学工业出版社, 2005: 96-97.
[2]梁成浩, 吕升忠.10万方原油储罐罐底内底板腐蚀与牺牲阳极阴极保护[J].管道技术与设备, 2004, 4:30-32.
[3]Grill S T, Skourup J, Svendsen I A. An efficient boundary element method for nonlinear water waves [J].Engineering Analysis with Boundary Element, 1989,6(2): 97-107.
[4]Amster P, De Napoli P. A quasilinearization method for elliptic problems with a nonlinear boundary condition[J]. Nonlinear Analysis: Theory, Method and Applications, 2007, 66(10): 2255-2263.
[5]Santiago J A F, Telles J C F. A solution technologies for cathodic protection with dynamic boundary conditions by the boundary element method [J]. Advances in Engineering Software, 1999, 30(11): 663-671.
[6]翁永基.阴极保护设计中的模型研究及其应用[J].腐蚀科学和防护技术, 1999, 11: 36-48.
[7]Brichau F, Deconinck J. A numerical model for cathodic protection of buried pipes [J]. Corrosion, 1994,50(1): 39-49.
[8]Kim Y G, Kim Y C, Kho Y T. BEM application for thin electrolyte corrosion problem [C]//Boundary Element Technology ⅩⅣ. Southampton:[s.l.]Computational Mechanics Publications, 2001: 87-93.
[9]邢少华, 李相波, 姚萍, 等.铜管道内壁铁牺牲阳极保护电位数值模拟计算[J].腐蚀与防护, 2008, 29(10):622-624.
[10]吴建华, 云凤玲, 邢少华, 等.数值模拟计算在舰艇阴极保护中的应用[J].装备环境工程, 2008, 5(3):1-4.
[11]Robert A Adey, John Baynham. Design and optimissation of cathodic protection systems using computer simulation [J]. Sea Technology, 1998, 35(6): 189-215.
[12]邢少华, 彭衍磊, 张繁, 等.压载舱阴极保护系统性能仿真及优化[J].装备环境工程, 2011, 8(1): 5-10.
[13]Santana Diaz E, Adey R. Predicting the coating condition on ships using ICCP system data [J]. Int J Numer Meth Engng, 2005, 62: 727-746.
[14]陆璐, 邢少华, 吴建华, 等.船舶腐蚀相关电磁场特征仿真研究[J].装备环境工程, 2011, 8(1): 24-28.
[15]陈顺杭, 梁成浩, 袁传军.数值方法在阴极保护中的应用和进展[J].全面腐蚀控制, 2006, 20 (5): 19-21.
[16]胡舸, 张胜涛, 向斌.Matlab在海底管线阴极保护电场计算中的应用[J].海洋科学, 2007, 31(12): 34-37.
[17]吕少泉.石脑油储罐罐底腐蚀原因浅析及对策[J].设备与腐蚀, 2005 (3): 160-161.
[18]GBT4948-2002.铝-锌-铟系合金牺牲阳极标准[S].
[19]GB 50393-2008.钢制石油储罐防腐蚀工程技术规范[S].

