并联电爆炸丝断路开关断流特性模拟与分析

顾 林，张 合，石秀丽

（南京理工大学 智能弹药技术国防重点实验室，江苏 南京，210094）

电磁脉冲弹、磁爆加载弹药等磁爆弹药的能量和动力都是由弹载磁通量压缩发生器提供的。磁通量压缩发生器往往采用高速断路开关将其电感储存的能量加载到负载上[1]。高速断路开关和磁通量压缩发生器的联合运行，可使得能量储存阶段和能量提取阶段分割开来，并保障了阻抗匹配和脉冲成形。电爆炸丝断路开关（Electro Explosive Breaker，EEB）的通断时间短、断路电流大、功率大、成本低，故在磁通量压缩器脉冲形成网络中应用最为广泛[2]。

电爆炸断路开关是一次性、破坏性开关，数值计算、模拟仿真对其设计有着重要作用。解放军理工大学工程兵工程学院朱翼超等人采用电阻率-比作用量模型，对含电爆炸丝元件的电路仿真模拟了整个电爆炸过程[3]。中国工程物理研究院蒋吉昊等人对电爆炸丝进行了一维磁流体模型数值模拟[4]。国防科技大学杨汉武等人则建立了PSpice模型进行了断流分析[2]。英国 Loughborough大学开展了脉冲变压器结合电爆炸丝断路开关技术的研究[5]。这些建立的模型尽管能很好地解释和符合实验数据，但模型建立复杂，调试参数不方便，不利于开关设计。SIMULINK仿真模型相比较于数值模拟直观，无需书写大量程序公式函数，同时也避免了数值模拟计算的复杂性和不通用性，故本文利用SIMULINK软件基于时变电阻模型，对并联电爆炸丝断路开关断流特性进行仿真分析，研究电爆炸丝的长度、根数和直径等参数变化对断路时间以及断路电流的影响。

1 电爆炸丝断路开关物理模型

电爆炸丝断路开关由许多根金属细丝并联组成，并联的电爆炸丝快速通过大电流时，金属丝先后经历固态、熔化、液态加热、汽化、电弧成长及爆炸等几个过程，见图1。爆炸断路开关断路初期，电阻率随着注入能量的增大而增大。当注入能量足够大时，金属导体材料解体，气化波阵面向导体内部运动，并发生爆炸，从而开关断开[6]。

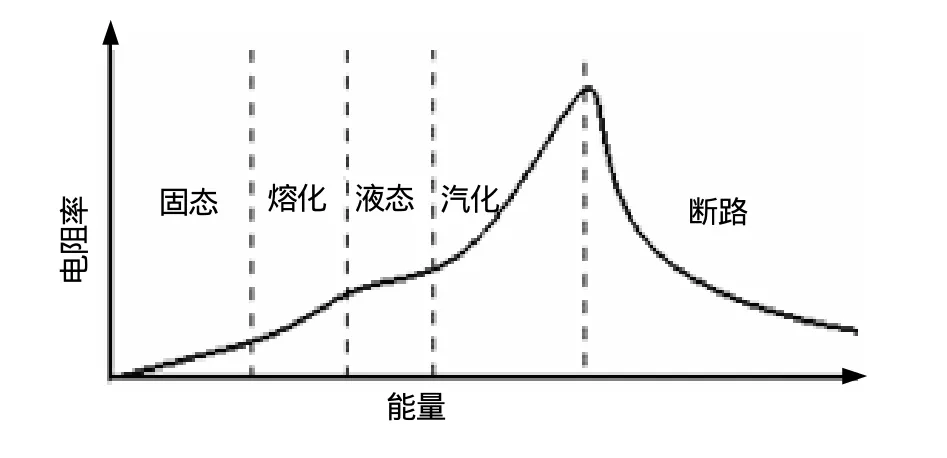
图1 典型电爆炸丝爆炸物理过程[6]Fig.1 Typical physical process of electrical explosion wires [6]

式（1）中：d为电爆炸丝直径， (0)R为电阻初始值，vv为气化波阵面的运动速度。式（1）的计算模型表明气化波在铜爆炸丝中传播速度vv和铜丝横截面积决定着电爆炸断路开关的电流通断时间。但是vv由于计算比较复杂，不适合做数值模拟。本文从Tucker模型来推导电爆炸丝的电阻率具体计算模型。

忽略热传导，由焦耳定律[7]：

式（2）中：γ为爆炸金属丝的能量密度；ρ为爆炸金属丝的电阻率；β为输入的电流密度。

爆炸金属丝的能量密度和爆炸金属丝的电阻率两者呈一定比例的关系：

式（3）中：下标τ=1,2，分别对应固态与液态；ρτ为最初电阻率；ετ为加热的效率。

由式（2）～（3）推导得出：

在固态加热结束时刻与液态加热结束时刻，式（4）可写为：

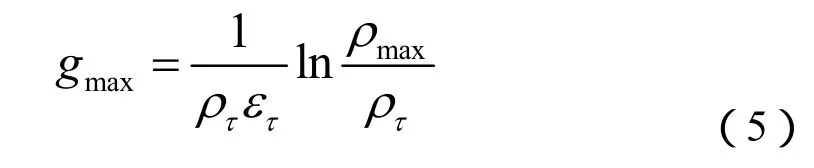
式（5）中：gmax为固态加热结束时刻的比作用量；ρmax为固态加热结束时刻的电阻率。又有：

将式（6）代入式（5）可得：

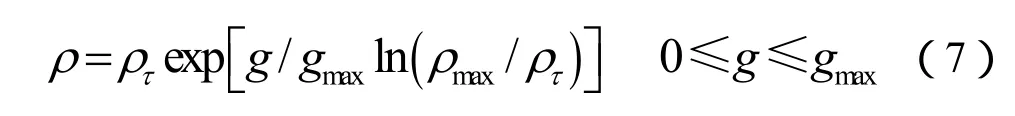
爆炸金属导体在经历固态转变为液态、液态转变为汽态的过程中能量的表达式为：

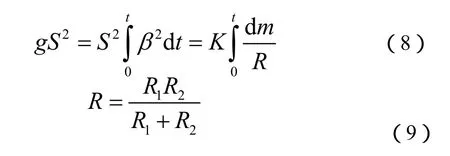
式（8）～（9）中：K为相变潜热；S为金属导体的截面积；m为金属导体原初的相质量；R为相1与相2的总电阻；R1、R2为相1与相2电阻。结合式（7）得出电阻率与比作用量的函数关系[3,8,9]：

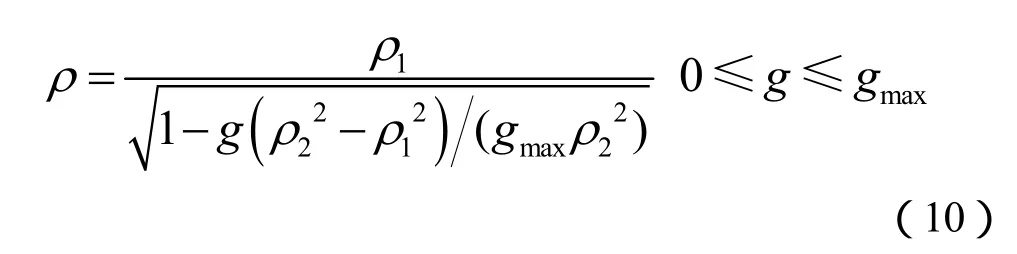
图2为文献[6]的比作用量和电阻率的实验数据，反映了ρ与g的大致函数关系，可以作为数值模拟仿真模型建立的参考。

利用电容器放电电路对电爆炸丝的断流特性进行分析，电容放电回路电爆炸丝起爆时间et的经验公式[10]：

式（11）中：L为回路电感；C为电容值；有关kj、kr的计算文献[3]中有详细方法，这里不再赘述。

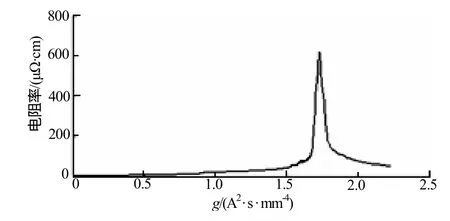
图2 ρ与g实验曲线(铜)Fig.2 Experimental curve of resistivity and specific action(Cu)

2 模型建立

采用Matlab软件的SIMULINK模块，建立电爆炸丝断流仿真模型，部分如图3所示。

图3 SIMULINK电爆炸丝断流仿真模型（部分）Fig.3 SIMULINK simulation model of EEB (parts)

根据上节的理论分析与推导的公式，利用积分模块对电流平方进行积分，经过增益得到相应的比作用量。铜电爆炸丝电阻故再次用增益模块得到相应的电阻。根据UIR= ，电压源由其两端的电流来控制。导通时，电容(SIMULINK中电容充电电压值可直接预置，无需充电)通过储能电感、回路电阻和电爆炸丝进行放电，简化等效为RLC回路，研究电爆炸过程的电学特性。

模型可以通过切断电压和切断电流波形直观地观察电爆炸丝的工作过程，从而可以分析电爆炸丝的切断电流、切断电压、切断时间以及切断效果之间的关系。模型取电容10μF、放电预置电压50kV、负载电感2.5μH。

3 断路特性仿真与分析

利用模型分析长度l、根数n以及直径d等参数单一变量对电爆炸丝的断路时间和断路电流等断流特性的影响。首先固定电爆炸丝根数n=30、直径d=0.05mm，改变长度l为100～500mm，研究电爆炸丝的断流特性，仿真结果见图4和表1。

图4 长度对电爆炸丝断流及电感两端电压影响Fig.4 Influence of length on EEB and inductor’s voltage

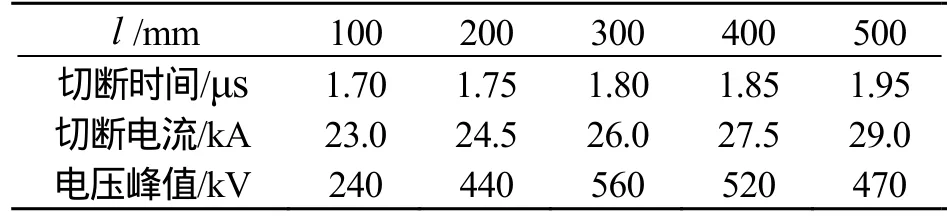
表1 长度l对断流特性影响Tab.1 Influence of length on current breaking characteristics

从表1可知长度l的变化对切断电流的时间以及切断电流峰值影响并不是太显著。图4显示，长度l影响了电爆炸丝断路开关切断电流的过程。长度l小于一定值时，内部产生的高电压会使导体击穿，将不会切断，出现后期不能彻底切断电流，无法恢复到零值的现象，仿真断流曲线准确地反映了这一点。储能电感两端的电压峰值随着电爆炸丝长度的增加，出现了变大再变小的变化曲线，从电压角度看长度l存在一个最优值。

固定直径d=0.05mm和长度l=500mm，改变根数n为30～90根，研究电爆炸丝的断流特性，仿真结果见表2和图5。

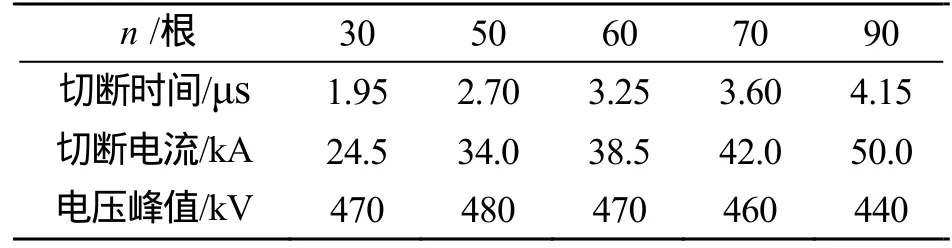
表2 根数对断流特性的影响Tab.2 Influence of amount on current breaking characteristics

图5 根数n对电爆炸丝断流及电感两端电压的影响Fig.5 Influence of amount on EEB and inductor’s voltage

由表2及图5可以看出，电爆炸丝根数n与切断时间近似存在线性关系，即电爆炸丝总横截面积与切断时间存在线性关系。n变多，电爆炸时间变长，且切断的电流值也变大。根数n变多，总横截面积增大，电流密度减小，达到爆炸所需的比作用量g的时间变长。当n大于一定数量时，电流密度太小，所供给的能量将不足以使电爆炸丝被切断。同时，跟长度l一样，随着电爆炸丝根数n的增多，储能电感两端的电压峰值出现了变大再变小的变化曲线。

固定根数n=30和长度l=500mm，改变直径d为0.05～0.10mm，研究电爆炸丝的断流特性，仿真结果见表3和图6。

表3 直径d对断流特性影响Tab.3 Influence of diameter on current breaking characteristics

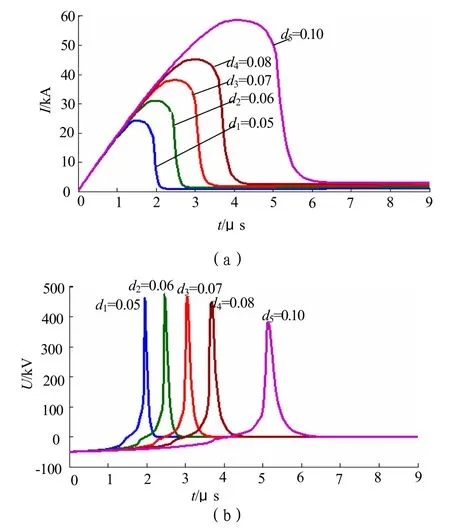
图6 直径d对电爆炸丝断流及电感两端电压影响Fig.6 Influence of diameter on EEB and inductor’s voltage

由表3和图6可见，随着电爆炸丝直径d的增大，切断电流的时间变长，切断的电流值也变大。储能电感两端的电压峰值随着电爆炸丝直径d的增大，先变大后变小。增大电爆炸丝直径d与电爆炸丝根数n的效果很接近，都等效增大了电爆炸丝的总横截面积。但实验表明[8]，在总横截面积一定时，选择n大d小的效果较好，因为这样的设计具有较低的电感[2,8]。因此可以对模型进行进一步的优化，增加电爆炸丝电感分布的不均匀性与随机性。

4 结束语

本文为了研究铜导体做并联电爆炸丝断路开关的断流特性，首先理论分析了电爆炸丝断路开关物理模型，在这基础上采用 SIMULINK建立了基于时变电阻模块的仿真模型。模型采用电容器脉冲放电对铜电爆炸丝断路特性进行分析，得出电爆炸丝根数、长度以及直径参数对断路时间和断路电流的影响规律。与其他模型相比较，基于 SIMULINK的电爆炸丝断流仿真模型更为直观便捷。仿真结果与文献[2]基于PSpice的仿真模型结果对应，根数、长度以及直径等参数对断流特性的影响规律也一致；并且也能很好地吻合文献[11]的实验结果，故此仿真模拟能够准确反映电爆炸丝的一般规律。本文的理论分析推导和仿真研究为设计并联电爆炸丝断路开关的参数选择提供了参考依据。

[1]孙承纬,周之奎,译.磁通量压缩发生器[M].北京：国防工业出版社,2008.

[2]杨汉武,钟辉. PSpice模型用于电爆炸丝的数值模拟[J].国防科技大学学报,2000(22):38-42.

[3]朱翼超,罗根新,方向,陈宇.电爆炸丝的电气特性[J].爆炸与冲击,2011,31(6):664-668.

[4]蒋吉昊,杨宇,胡熙静,王钢华.电爆炸丝 1维磁流体模型数值模拟[J].强激光与粒子束,2006,18(3):463-466.

[5]B.M.Novac, I.R.Smith, K.Gregory. High-power high-voltage generator with a multi-pulse twin output[C]//13th IEEE Internatinal Pulse Power Conference. Las Vegas :IEEE Press,2001.

[6]龚兴根.电爆炸断路开关[J].强激光与粒子束,2002,14(4):577-582.

[7]Tucker T J，Toth R P. A . Computer code for the prediction of the behavior of electrical circuits containing exploding wire element[R].Albuquerque: Sandia Laboratories,1975.

[8]石秀丽.磁通量压缩发生器关键技术研究[D].南京:南京理工大学,2011.

[9]杨汉武. 爆炸磁压缩发生器及其脉冲功率调制研究[D].长沙:国防科学技术大学, 2002.

[10]曾正中. 实用脉冲功率技术引论[M].西安：陕西科学技术出版社,2003.

[11]Howard S. Leoplod. Effect of bridgewire parameters on explosive initiation[J]. Exploding Wires, 1964(3):125-152.