水下爆炸冲击波相互作用的仿真分析

盛振新，刘荣忠，郭 锐

（南京理工大学机械工程学院 智能弹药国防重点实验室，江苏 南京， 210094）

在同一片水域多个炸药发生爆炸时，爆炸冲击波会相互影响，而目前对于冲击波之间相互作用的研究尚少。大量论文对单个炸药水下爆炸进行了仿真计算[1-5]，主要是利用 AUTODYN、MSC.DYTRAN 和LS-DYNA等动力学仿真软件。张振华[1]和肖秋平[3]分别利用MSC.DYTRAN和AUTODYN计算了球形药包在无限水域中的爆炸过程，分析了网格密度和水的状态方程参数对水下爆炸冲击波的影响。吴国群等人[5]利用两发电雷管进行水下爆炸试验，模拟研究两个相同药量药包水下爆炸形成的冲击波之间的相互作用，结果表明起爆延时和间距的改变会对水下爆炸冲击波之间的相互作用有较大影响。为了更加直观地研究水下爆炸冲击波之间的相互作用，本文利用AUTODYN对两发炸药水下爆炸冲击波进行仿真计算，深入研究水下爆炸冲击波之间的相互作用，为提高水下爆炸的威力提供一定的理论参考。

1 炸药水下爆炸数值模拟

1.1 仿真模型

文中利用AUTODYN动力学仿真软件，对炸药水下爆炸的过程进行仿真计算，为了避免 Lagrange算法经常遇到的网格大变形所导致的计算困难，采用Euler算法。

建立二维面对称有限元模型，计算模型水域尺寸为1 000mm×500mm，设置网格数为500×250，两发TNT球形裸装炸药半径均为20 mm，质量为54.62 g，装药间距为100mm，采用中心起爆方式，模型及相关尺寸如图1（a）所示。为了将单发炸药水下爆炸冲击波和两发炸药水下爆炸冲击波进行对比分析，还需建立单发炸药的计算模型，如图1（b）所示。

图1 计算模型及相关尺寸Fig.1 Model and geometry

图1模型中，以1#和2#炸药中心连线的中点作为圆心，以 450mm 作为半径，1#、2#和 3#传感器分布在半径为 450mm的圆上。3#传感器的布置是为了研究两发炸药同时起爆和延时起爆时，相同传播冲击波之间的相互作用。1#和2#传感器是关于1#和2#炸药中心连线的中点对称分布的，是为了研究延时起爆时相对位置和延时起爆对冲击波之间相互作用的影响。

1.2 参数设定

本研究采用多项式状态方程描述水的状态方程，炸药采用JWL状态方程。

1.2.1 水的多项式状态方程

水的多项式状态方程根据压缩状态的不同具有不同的形式。

当水压缩时（μ＞0）时，状态方程为：

当水膨胀时（μ＜0），状态方程为：

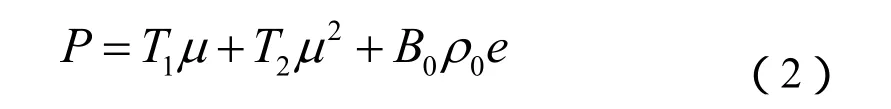
当水既不压缩也不膨胀时（μ=0），式（2）和（3）可以简化为同一形式：

式（1）～（3）中：P为水中压力；μ为压缩比，为水的内能；ρ0为水密度，取ρ0=1g/cm3。A1=2.2×106kPa，A2=9.54×106kPa，A3=1.457×107kPa，B0=B1=0.28，T1=2.2×106kPa，T2=0。

1.2.2 TNT炸药的JWL状态方程式

TNT炸药的JWL状态方程式为：

式（4）中：P为压力；V为相对体积；E为内能；A和B为材料参数；R1、R2和ω为常数。取A=3.712×1011Pa，B=3.23×109Pa，R1=4.15，R2=0.95，ω=0.30，初始内能E0=4.29×106J/kg。

2 计算结果及分析

2.1 计算结果

单发炸药水下爆炸冲击波的计算结果见表1。图1（b）中1#、3#和2#传感器相对于1#炸药的距离是递增的，表1数据显示，1#、3#和2#传感器测得的1#炸药爆炸冲击波的峰值压力随着距离的增加而减小，传播时间随着距离的增加而增加。

表1 单发炸药水下爆炸冲击波峰值压力Tab.1 Peak pressure of shock wave generated by single explosion

为了分析起爆延时对两发炸药水下爆炸冲击波相互作用的影响，在炸药间距不变、起爆延时变化的情况下，计算得到3个传感器处的冲击波峰值压力，如表2所示。

表2 不同起爆延时情况下的两发炸药水下爆炸冲击波峰值压力Tab.2 Peak pressure of shock wave generated by two explosions with different detonation delay

2.2 同时起爆对冲击波压力的影响

当两发炸药同时起爆时，压力流场分布如图2所示。

图2 同时起爆压力流场分布图Fig.2 Pressure field of coinstantaneous detonation

1#和2#传感器是关于1#和2#炸药中心连线的中点对称分布的，其测得的压力曲线应该是相同的，所以主要分析1#传感器测得压力曲线。

1#炸药和 2#炸药产生的冲击波先后到达 1#传感器，测得冲击波压力如图3（a）所示，1#传感器测得的1#炸药和2#炸药的爆炸冲击波先后到达，其峰值压力P先和P后分别为250.3MPa和180.9MPa。P先和单发炸药的冲击波峰值压力250.5MPa几乎相同，这是因为1#炸药与1#传感器的距离相对2#炸药与1#传感器的距离较近，在冲击波向1#传感器传播的时候，2#炸药的爆炸冲击波在1#炸药的爆炸冲击波之后，所以没有影响。

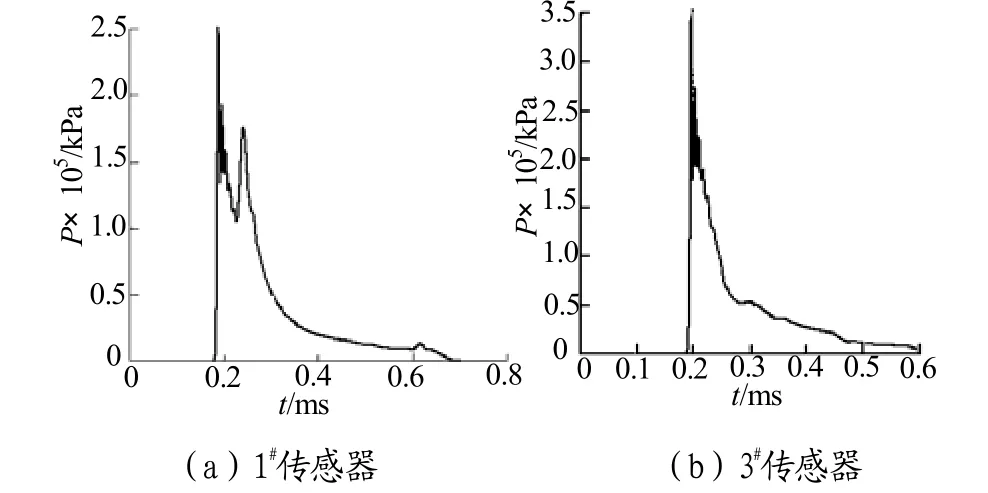
图3 同时起爆时1#和3#传感器测得的压力曲线Fig.3 Pressure curve at 1# &3# sensor under simultaneous detonation

1#传感器测得的 2#炸药冲击波峰值压力p后为180.9MPa，比相同距离单发炸药冲击波峰值压力195.6MPa小。虽然两发炸药同时起爆，但两者之间存在100mm间距，2#炸药冲击波传播到1#传感器的过程中要透过1#炸药爆炸时产生的气泡，冲击波会产生透射和绕射，部分还会被反射并产生稀疏波，所以到达1#传感器的2#炸药冲击波峰值压力偏小。

3#传感器在两发炸药连线的中垂线上，其到1#炸药和2#炸药的距离相同，相同的爆炸冲击波P先和P后于同一时刻在 3#传感器处发生斜碰撞，冲击波压力就会产生叠加，如图 3（b）所示。3#传感器测得的两发炸药同时起爆时峰值压力为 353.0MPa，单发炸药在相同位置处的冲击波峰值压力为 218.9MPa，从数值可以看出，冲击波压力的叠加不是简单的加法。

2.3 起爆延时对冲击波压力的影响

2.3.1 起爆延时为 5～10μs

当两发炸药起爆延时为5μs时，流场压力如图4所示，冲击波压力曲线如图5所示，表2中数据显示，随着起爆延时的增加，1#传感器测得的P先几乎不变，P后逐渐变小。这说明起爆延时增大，1#炸药爆炸产生的气泡越大，对2#炸药冲击波造成的衰减越大。

随着起爆延时的增加，2#传感器测得的P先几乎不变，P后逐渐变大。这说明起爆延时增大，2#炸药爆炸产生的气泡不但不会对1#炸药冲击波产生衰减，反而会起到增强的作用。

图4 5μs延时起爆流场压力分布图Fig.4 Pressure field of explosions with 5μs delay

随着起爆延时的增加，3#传感器测得的冲击波压力稍有增加，考虑增加幅度很小，可把它当作计算误差，不再进行分析。

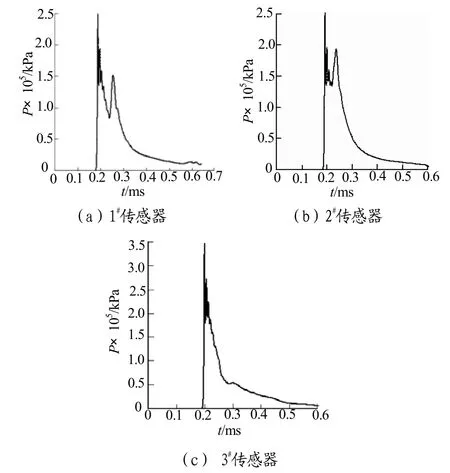
图5 5μs延时传感器测得的压力曲线Fig.5 Pressure curve at sensors with 5μs delay

2.3.2 起爆延时为 20～30μs

在计算过程中发现，起爆延时约为13μs时，1#炸药爆炸产生的冲击波就把2#炸药引爆了，这种现象称之为“殉爆”，延时20μs的流场压力如图6所示，冲击波压力曲线如图7所示。所以，当两发炸药起爆延时为20～30μs时，3个传感器所测冲击波压力是不变的。

图6 20μs延时起爆流场压力分布图Fig.6 Pressure field of explosions with 20μs delay

对比起爆延时20μs和10μs的数据，可见1#传感器测得的P后减小了，2#传感器测得的P后增大了，这同2.3.1节中的分析结论相同。

值得一提的是，2#传感器测得的P先比起爆延时为5～1 0μs时的P先偏小。1#炸药爆炸产生的冲击波引爆2#炸药时，2#炸药的起爆方式不再是中心起爆，而是靠近1#炸药的偏心起爆，从而使爆炸冲击波压力变小。

图7 20μs延时传感器测得的压力曲线Fig.7 Pressure curve at sensors with 20μs delay

2.4 起爆延时对到达延时的影响

两发炸药同时起爆时，爆炸冲击波到达 1#和 2#传感器的到达延时同为 53.3μs，和单发炸药爆炸冲击波到达各传感器的延时几乎相同，其路程差即两发炸药间距为 100mm，计算得到冲击波传播速度为1 876.2m/s，大于理论的水中声速，说明在此时间段内，爆炸冲击波还未衰减到水中声速。

起爆延时为5μs时，1#和2#炸药爆炸冲击波到达1#传感器的延时为 65.6μs，大于(53.3+5) μs；冲击波到达2#传感器的延时为44.5μs，小于(53.3-5) μs。起爆时延为10μs时，情况同样如此。由此可见，1#炸药爆炸产生的气泡不仅会引起 2#炸药冲击波的衰减，还会降低2#炸药冲击波的传播速度；相反，2#炸药爆炸不仅会增强1#炸药的爆炸冲击波，还会使其传播速度加快。

3 结论

为了研究水下爆炸冲击波之间的相互作用，利用AUTODYN仿真软件计算两发炸药水下爆炸冲击波压力，通过分析计算结果，得出以下结论：

（1）两发炸药同时起爆的情况下，炸药爆炸产生的气泡会对临近炸药的爆炸冲击波产生衰减的作用；

（2）两发炸药延时起爆且不会引起殉爆的情况下，在距先起爆炸药较近处，先起爆炸药产生的气泡会对后起爆炸药的冲击波产生衰减作用，并且会使冲击波的传播速度变慢；而在距后起爆炸药较近处，后起爆炸药的爆炸会对先起爆炸药的冲击波产生增强的作用，并且会使冲击波的传播速度变快；

（3）两发炸药延时起爆且因其殉爆的情况下，后起爆炸药的起爆方式由中心起爆变为偏心起爆，其爆炸冲击波会变小，除此之外，均与结论（2）相同。

在工程实践中，本文所得结论可为提高水下爆炸的威力提供一定的理论参考。

[1]张振华,朱锡,白雪飞.水下爆炸冲击波的数值模拟研究[J].爆炸与冲击,2004,24(2):182-187.

[2]贾宪振.基于通用程序的水下爆炸及其对结构作用的数值模拟研究[D].南京：南京理工大学,2007.

[3]肖秋平, 陈网桦, 贾宪振,等. 基于 AUTODYN 的水下爆炸冲击波模拟研究[J].舰船科学技术, 2009,31(2):38-43.

[4]刘科种,徐更光,辛春亮,等.AUTODYN 水下爆炸数值模拟研究[J].爆破,2009,26(3):18-21.

[5]Jia Xian-zhen. Numerical simulation of underwater explosion and its effect on structure based on commercial softwares[D].Nanjing: Nanjing University of Science and Technology,2007.

[6]吴国群, 张明晓,弓启祥,等. 水下爆炸冲击波相互作用的研究[J].煤矿爆破,2011,93(2): 12-15.