fMRI盲信号分离中的时间和空间独立成分分析法的时空特性比较

高欣，边倩，熊金虎

1.中科院苏州生物医学工程技术研究所 医学影像室，江苏 苏州 215163；2.第二炮兵工程大学 指挥自动化系，陕西 西安 710025；3.爱荷华大学放射科，爱荷华州 美国

fMRI盲信号分离中的时间和空间独立成分分析法的时空特性比较

高欣1，边倩2，熊金虎3

1.中科院苏州生物医学工程技术研究所 医学影像室，江苏 苏州 215163；2.第二炮兵工程大学 指挥自动化系，陕西 西安 710025；3.爱荷华大学放射科，爱荷华州 美国

目的 采用空间独立成分分析法（sICA）和时间独立成分分析法（tICA）对功能磁共振成像（fMRI）信号进行分离，比较信号间的时空特性对2种独立成分分析方法性能的影响。方法 模拟fMRI数据，并将2组独立的信号以及它们的线性混合信号叠加到空间独立的区域，分别利用Infomax、Combi、FBSS和ICA-EMB 4种算法实现sICA和tICA，并对模拟数据中的3组信号进行提取和分离。结果 sICA只能分离空间独立且时间高度独立的信号，无法分离空间相关、时间独立的信号；tICA不仅能够准确分离空间和时间高度独立信号，而且能够准确分离空间高度相关、时间独立的信号，并将时间相关信号整体提取；FBSS和ICA-EMB 2种算法较Infomax和Combi性能稳定。结论 空间或时间独立性假设违背到一定程度时，sICA和tICA对信号分离的结果存在差异。应根据需要选择适合的sICA或者tICA方法对fMRI数据进行处理。

脑功能磁共振成像；独立成分分析法；空间独立成分分析法；时间独立成分分析法；

功能性磁共振成像（functional Magnetic Resonance Imaging ，fMRI），是一种通过测量神经放电引起局部磁场改变推测神经元活动信息的技术。fMRI图像是一组时间序列的3D图像，随时间变化的神经活动信号被记录在4D数据中。独立成分分析方法（Independent Component Analysis，ICA）是一种在不知混合模型又不知信号源分布的情况下，从线性混合信号中恢复一些非高斯且相互独立信号的技术。待分离的隐藏信号被称为数据处理中的独立成分[1]。ICA能够将一组图像序列（4D）分解成空间或者时间独立成分：空间独立成分表现为一组成分图谱；时间独立成分表现为一组相关的时序波形（波形图）。ICA有2种分析方法：空间ICA（Spatical ICA，sICA）和时间ICA（Temporal ICA， tICA）。sICA能够获取表现相互独立成分的图像和这些独立成分相关的时序波形；而tICA能够获取独立成分的时序波形和与其相对应的图像。与其他传统的fMRI分析方法相比，ICA在fMRI数据分析的优势是：无论是sICA还是tICA均不需要参考函数（明确的时间模型）或者预定义的种子区域。对fMRI数据分析，常用sICA抽取一个特定的成分或者使用脑部结构和功能知识自动地获取图谱[2-7]。tICA常用于脑电图（EEG）和诱发脑电位（Event-Related brain Potential，ERP）的数据分析[8-11]，而其在fMRI中的应用报道尚不多见。一些学者[12-14]对sICA和tICA在fMRI数据分析的性能进行了研究。研究表明，对任务相关组分的实验，sICA和tICA能够得到相似的结果。然而，迄今为止，针对sICA与tICA对fMRI数据信号分离和提取的深入评价研究，特别是关于待分离信号的时空特性对sICA和tICA性能影响的评价研究尚未见报道。本文基于模拟数据实验，评价sICA和tICA对具有不同时空特性的信号进行分离的性能。此外，针对空间定位和时序确定的精度，比较了不同类型的ICA对信号检测的性能。研究最终建立了一种从不同时间独立性，但相同空间独立性的多个信号中检测某一特定信号的策略。

1 材料和方法

1.1 数据模拟

为了评价信号时空特性对sICA和tICA在信号分离中性能的影响，以及不同种类的ICA对信号分离的效果，研究中模拟一组fMRI数据。以一个切片的回波平面成像（Echo-Planar Imaging，EPI）扫描图像（图1）作为一个3D体数据（64×64×1）个体素，该3D体数据复制700次构建具有700个时间点的无噪声4D-fMRI数据。TR设定为0.3 s，信号时长210 s。2个模拟信号：一个表示生理信号，另一个表示事件相关的脑血流动力学信号。生理信号为模拟心脏的信号（频率为1.3 Hz）[15]，简化处理，由Gamma波形以0.13 Hz重复频率构成（信号A）；另一个是由方波构成的信号，重复频率0.09 Hz，1.2 s的高电平接2.4 s的低电平（信号B），信号A和信号B是相关独立的2个信号（相关度）。2个信号的线性组合（叠加）构成第3个信号（信号C）。信号C和信号A的相关度是0.54，信号C和信号B的相关度是0.85。这3个信号分别叠加到具有700个时间点的无噪声fMRI数据中的指定区域，每个信号占2个区域（4×4×1）。3个信号的排列次序从下到上依次是A、B、C。为了模拟脑部噪声环境，研究中，在整个脑部图像区域增加随机噪声，该噪声服从均值为0、方差为1的高斯分布，信噪比设定为10 dB。

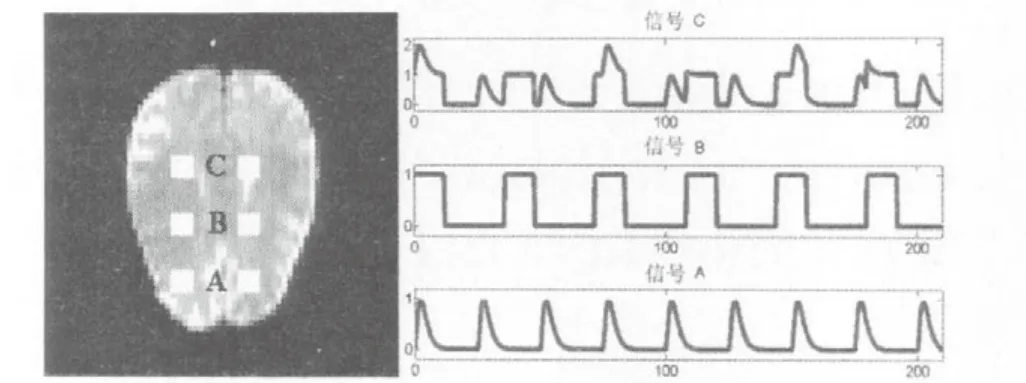
图1 一个EPI扫描图像

1.2 数据处理

基于独立成分少于时间点（sICA）或者空间点（tICA）的假设，首先采用主成分分析（Principle Components Analysis，PCA），在维数上简化fMRI数据，选取20个独立成分作为初始值，然后采用ICA对其进行处理。

对于sICA，输入数据是一个N ×M矩阵（N表示时间点数，N=700，M表示体素值，M=64×64）。输出是20个空间独立成分，每个成分包含M个体素，即图谱，20个独立成分均各自有时序波形图。

tICA方法的输入数据是一个M×N的矩阵，M和N含义同上。输出为20个时间独立的成分，每个成分含有700个时间点的时序，并对应一个M个体素的图谱。无论是sICA还是tICA，ICA均可获得20个时序以及和与其相对应的图谱。

最后采用Z-MAP方法将图谱阈值化，并重叠在EPI图像上。对于sICA和tICA，我们分别采用Infomax[16]，Combi[17]，FBSS[18]和 ICA-EBM[19]等算法来实现。

2 结果

采用不同sICA方法对模拟数据进行信号分离的结果，见图2。结果表明，Infomax，FBSS和ICA-EBM算法均可分离出空间域和时间域高度独立的区域A（Gamma波信号，信号A），但无法分离出空间域独立、时间域与区域A相关的区域C（包含Gamma波信号）。无论空间域独立与否，3种算法均无法在时间域检测到方形波信号（信号B），只是将所有具有方形波信号的区域提取出来（区域B和C）。这3种算法中，就检测到的波形图的精度而言，FBSS和ICAEBM算法比Infomax算法性能更为稳定。Combi算法虽然能从空间域上将信号Gamma区域检测出来，但时间序列图不正确。

图2 sICA对模拟数据处理结果

采用 4种 tICA算法 Infomax、Combi、FBSS和 ICAEBM对模拟数据进行测试的结果，见图3。结果表明，4种算法均可准确分离出空间域独立的Gamma波信号（信号A），而且还能分离出与信号A空间独立但时间相关的信号C（区域C）。除Infomax以外的其他3种算法均可分离出空间域独立的方形波信号（信号B），及其与信号B空间独立但时间相关的信号C（区域C）。Combi、FBSS和ICA-EBM3种tICA算法准确度一致，Infomax算法性能较弱。

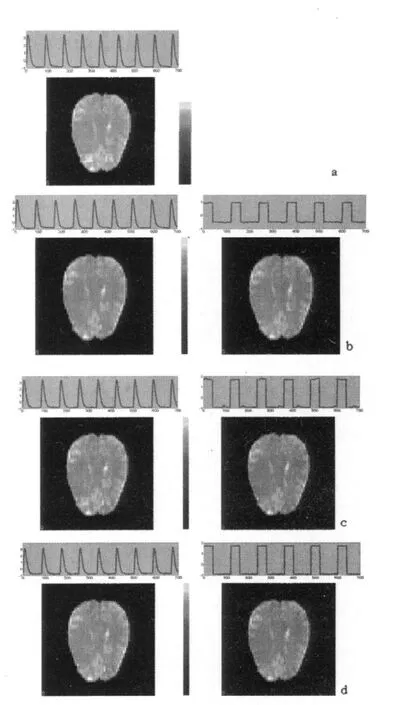
图3 tICA对模拟数据处理结果

将图2和图3比较发现，tICA不仅能够将空间域独立、时间域独立的信号分离，而且还能够将空间域相关、时间域独立的信号成功分离。sICA只能将空间与时间高度独立的信号分离，无法将空间域相关、时间域独立的信号分离。两种ICA对信号时空独立性的分离能力，见表1~2。

表1 sICA对信号时空独立性的分离能力

表2 tICA对信号时空独立性的分离能力

3 结论与讨论

sICA和tICA这两种ICA方法均能够分离统计学上假定相互独立的信号。然而，当空间或时间独立性假设违背到一定程度的时候，sICA和tICA对信号分离的结果则有所差异。实验表明，sICA和tICA均能成功地分离空间域和时间域均高度独立的信号，如信号A和信号B，二者的相关系数仅为0.0043，即相互独立。但对于空间域独立、时间域相关的信号，sICA无法准确进行分离，具体表现为：sICA即便能够获得空间独立成分图谱，也无法准确获得时序波形图；而tICA则可以实现准确分离，并获得正确的时序图。对于空间域高度相关、时间域独立的信号，sICA无法分离；而tICA能够成功分离。Infomax、Combi、FBSS和ICA-EBM4种算法比较，FBSS和ICA-EBM性能更加稳定。

通过结果分析， tICA具有空间独立时间相关信号整体提取分离能力，而sICA不具备。我们可以利用这个特点设计一种从多个不知源信号的混合信号中检测特定信号源的脑功能信号的分析方法，如脑部某区域一个特定信号夹在一些生理信号（心跳、呼吸）中，可采用如下方法将这个特定信号检测分离出来：用该特定信号源激发其它区域，利用tICA方法，将所有具有该信号源的区域提取分离出来，这样就能验证混合信号源中是否包含该特定信号。下一步，我们将设计实验，利用实际fMRI扫描数据去验证我们提出的这一信号检测方法的性能。

[1] Hyvärinen A, Karhunen J,Oja E. Independent Component Analysis[M]. John Wiley & Sons,2001.

[2] McKeown MJ,Makeig S,Brown GG,et al. Analysis of fMRI data by blind separation into independent spatial components[J].Human Brain Mapping,1998,6(2):160-188.

[3] 公昱文,张桂芸,马洪芝.ICA算法在fMRI中的应用[J].计算机工程与科学,2008,(10):37-39.

[4] 龙志颖,姚力,赵小杰,等.空间ICA在fMRI数据上的应用与分析[J].中国医学物理学杂志,2003,(4):219-221.

[5] 王世杰,罗立民.基于空间约束的时间独立成分分析方法分析fMRI数据[J].生物医学工程学杂志,2007,(6):1205-1210.

[6] 朱连云.独立成分分析在fMRI数据处理中的应用[D].浙江:浙江大学,2008.

[7] Biswal BB,Ulmer JL.Blind source separation of multiple signal sources of fMRI data sets using independent component analysis[J].Journal of Computer Assisted Tomography,1999,23(2): 265-271.

[8] Chiappa S,Barber D.Generative Temporal ICA for classification in asynchronous BCI systems [C].The 2nd International IEEE EMBS Conference On Neural Engineering. Washington D.C.,USA,2005.

[9] Jean G.Automatic removal of eye movement artifacts from the EEG using ICA and the dipole model[J].Progress in Natural Science,2009,9:1165-1170.

[10] 谢松云,张伟平,潘辉.ICA方法用于脑电信号α波提取的研究[J].计算机工程与应用,2008,(29):217-219.

[11] 何付志.独立分量分析在脑电信号分析中的应用[D].济南:山东大学,2005.

[12] Kim Petersen,Lars Kai Hansen,Thomas Kolenda,et al.On the Independent Components of Functional Neuroimages[C].Third International Conference on Independent Component Analysis and Blind Source Separation.Helsinki,Finland,2000: 615-620.

[13] Calhoun VD,Adali T, Pearlson GD,et al. Spatial and temporal independent component analysis of functional MRI data containing a pair of task-related waveforms[J].Human Brain Mapping,2001,13(1):43-53.

[14] Stone JV,Porrill J,Buchel C,et al.Spatial,temporal and Spatiotemporal independent component analysis of fMRI data[C]. 1999.

[15] Ma L,Wang B,Chen X,et al.Detecting functional connectivity in the resting brain:a comparison between ICA and CCA[J].Magnetic Resonance Imaging,2007,25(1):47-56.

[16] Bell AJ,Sejnowski TJ. Aninformation maximization approach to blind separation and blind deconvolution[J]. Neural Computation,1995(6):1129-1159.

[17] Tichavsky P,Koldovsky Z,Yeredor A,et al.A hybrid technique for blind separation of non-Gaussian and time-correlated sources using a multicomponent approach[J].IEEE Transactions on Neural Networks,2008,19(3):421-430.

[18] Li XL,Adali T.Blind spatiotemporal separation of second and/or higher-order correlated sources by entropy rate minimization[C].2010 IEEE International Conference on Acoustics,Speech and Signal Processing (ICASSP).Dallas,TX IEEE Xplore,2010:1934-1937.

[19] Li XL,Adali T.Independent component analysis by entropy bound minimization[J].IEEE Transactions on Signal Processing,2010,58(10):5151-5164.

Comparison of Spatiotemporal Characteristics of Spatial and Temporal Independent Component Analysis for Blind Source Separation in fMRI Data

GAO Xin1, BIAN Qian2,
XIONG Jin-hu3
1. Medical Imaging Studio, Suzhou Institute of Biomedical Engineering and Technology Chinese Academy of Science, Suzhou Jiangsu 215163, China;2. Automatic Command College, The Second Artillery Engineering University,Xi’an Shaanxi 710025, China;
3.Radiology Department, The University of Iowa, Iowa, America

R445.2； TN911.72

A

10.3969/j.issn.1674-1633.2012.08.008

1674-1633(2012)08-0033-04

2012-03-04

2012-05-22

国家自然科学基金资助项目（81000651）；江苏省自然科学基金资助项目（BK2010236）；美国国家卫生研究所NIH

基金资助项目（R21 MH 082187-01）。

本文作者：高欣，博士，美国爱荷华大学医院放射科博士后，中

科院苏州生物医学工程技术研究所 中科院“百人计划”研究员。

作者邮箱：xgao_bj@yahoo.com.cn

信号分离

Abstract: Objective Separate the fMRI signals by using spatial independent component analysis (sICA)and temporal independent component analysis (tICA). Compare the spatiotemporal characteristics among signals which has effect to performance analysis of two kinds of independt signals. Method Simulate fMRI data. Two sets of independent signals and their linear mixture were added in spatially independent regions. sICA and tICA were achieved by using respectively Infomax, Combi, FBSS and ICA-EMB.Then three sets of signals were applied to separate and extract from simulated fMRI. Results sICA can only separate signals spatially independent and highly temporally independent, can not separate spatially correlated and temporally independent signals. tICA is not only able to separate highly spatially and temporally independent signals, but also able to successfully separate highly spatially correlated and temporally independent signals, moreover, it can integrally extract temporally correlated signals.FBSS and ICA-EMB algorithms are more stable than Infomax and Combi algorithms. Conclusion The assumption of spatial or temporal independence is violated to a certain degree. There are certain difference of performance between sICA and tICA. It should be based on the characteristics of signals and requirement to select adaptive sICA or tICA method to fulf i ll blind signal separation in fMRI data.

Key words: fMRI; independent component analysis; spatial independent component analysis; temporal independent component analysis; signal separation