三维脉动源格林函数的一种简化算法
刘 磊,贾敬蓓,刘大路,黄亚南
(1.中国船级社天津分社,天津300457;2.大连海洋大学航海与船舶工程学院,辽宁大连116023)
0 引言
在水动力学研究中,经常采用格林函数建立方程求解速度势函数,进而分析流体对结构的作用力以及结构的运动响应。针对不同的实际问题,需要采用不同的格林函数。很多学者从不同角度、采用不同的方法对各种形式格林函数的数值计算方法进行了研究,以期能够更加快速、准确的计算格林函数。
许多学者对三维移动脉动源的数值计算方法进行了广泛深入的研究[1~3]。关于频域格林函数和时域格林函数的数值计算方法,也有不少学者进行了许多的研究工作[4~6]。然而,目前为止,针对三维脉动源格林函数的数值研究并不多。纪刚[7]和陈崧等[8]采用零阶 Bessel函数的 Laplace变换,将无航速具有自由液面的三维脉动源格林函数变形为易于截断处理的形式,实现了无穷积分向有限积分的转变,并采用了样条差值技术和自适应方法解决了高频振荡函数的数值积分的速度和精度问题。
本文主要针对三维脉动源,在分析其格林函数形式特点的基础上,对三维脉动源格林函数的数值计算问题进行了简化研究。
1 Bessel函数的三个积分

在 John V.Wehausen和 Edmund V.Laitone于1960年发表的文章《Surface Waves》中,给出了三维脉动源的一种格林函数形式:式中:k为波数空间的自变量;v为无限水深波数,,其中,ω 为波动角速度,g为重力加速度;J0(kR)和J0(vR)分别是kR和vR的零阶Bessel函数;r为场点和源点之间的距离,r=R为场点和源点之间的水平距离y,z)是场点坐标,(ξ,η,ζ)是源点坐标。
在靠近自由表面的位置z=ζ=0,因此式(1)可以变化为下面形式:
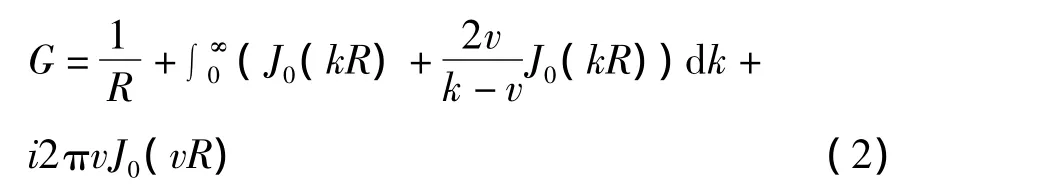
由式(2)可以看出,式(1)最终可以归结为求以下三种形式的Bessel函数积分,即:
如果直接在这种格林函数表达形式的基础上进行计算,过程比较繁琐。因此,本文从上述格林函数所包含的三种Bessel函数积分形式入手,对这种三维脉动源格林函数进行分析和简化,进而提出了一种简化算法。

编制FORTRAN程序即可求得使计算量比较少,又能在μ的取值比较小的时候满足精度要求。以μ为自变量,积分值为因变量,得到如图1的曲线。
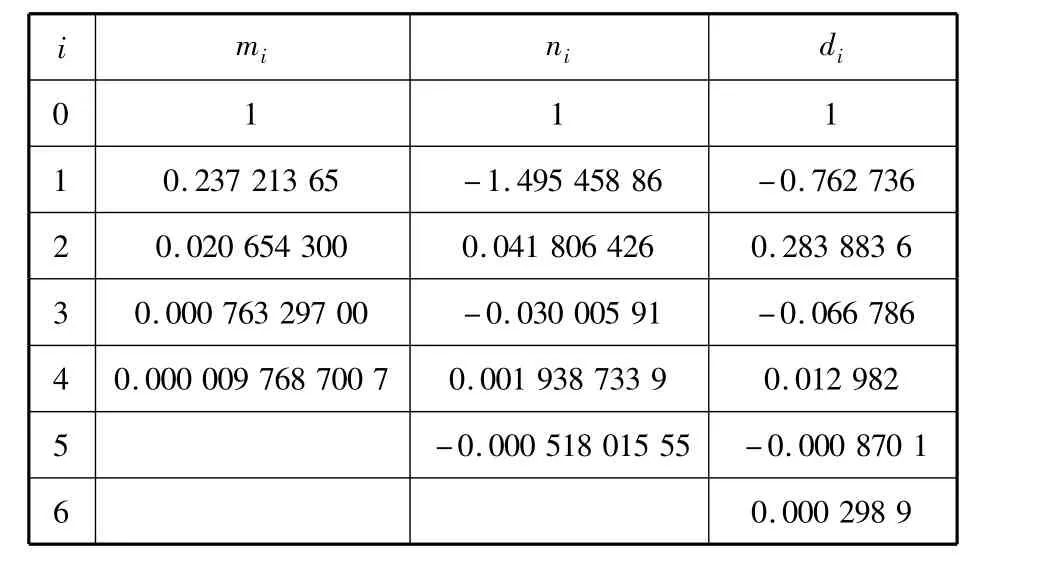
表1 系数值
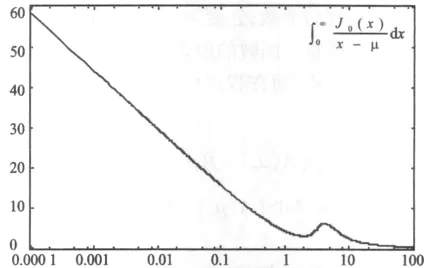
图1 积分曲线
2 积分曲线的拟合
在得到图1的曲线后,就期望通过已有的数据获得一个函数f(μ),要求这个函数可以比较好的符合得到的曲线。那么,在以后的计算中就可以在误差允许的范围内使用拟合出的函数来求出需要的数值。除了在精度上对拟合函数有要求外,还要求所得函数的形式相对简单。相反如果函数形式很复杂,计算步骤很繁琐甚至比直接计算还费时,就失去了进行这项工作的意义,也与初衷不符。
2.1 拟合方法及结果
拟合函数的优化方法有很多中可供选择,但是为了使得到的函数形式尽量简单,所以选择使用G-A算法和可变误差多面体算法。这两种算法的缺点在于需要先大致确定出函数的形式,然后才能通过程序求出各项系数的值。优点是操作比较简单,而且在函数形式相对简单的前提下精度基本符合要求。前期使用的是G-A算法,但是所得到的结果并不理想。而使用可变误差多面体算法,在初始函数形式以及系数个数相同的前提下,后者明显比G-A算法的精度要好。这并不是说G-A算法不好,而是说明在这个函数的拟合过程中,可变误差多面体法更合适。可变误差多面体法的计算过程实际上是一个可变多面体的寻找过程,也就是通过反射、膨胀、压缩和收缩来改变多面体。但是在寻找过程中得到的每一个点若不在近似能行区域内,就要经过一个恢复过程,用过程中得到的一个属于近似能行区域中的点来代换。这样可以保证可变多面体算法是在能行区域中进行的。
通过在[0.000 1,100]上得到的曲线,即图 1,可以看到:在[0.000 1,1)上,函数基本以对数形式衰减;在(10,100]上,函数则以幂函数1/x的形式衰减;在[1,10]上,函数出现了波动。由此推断,该拟合函数是对数函数和幂函数的复合函数。确定函数的形式后,系数的个数由少到多进行试验,尝试的范围最少为3个,最多为15个。在这个过程中,除了要改变系数的个数,还要对给出的函数形式及目标函数进行调整。函数的形式是基于对数函数和幂函数的基本性质,而在程序中目标函数有2种形式可供选择。


当对数函数的系数包含二次以上的项时,在[0.000 1,1)上会产生波动,所以选择以关于x的一次函数作为对数函数的系数。此外分子部分还有x2项和x3项,而分母部分的最高次数为四次,这种形式既可以保证在区间[1,10]上会产生波动,又能使当x的值比较大时候函数以1/x的形式衰减。在式(9)的基础上,经过比较采用式(7)作为目标函数,得到了表2的9个系数值。将系数值代入式(8),所得结果如图2所示。
由图2可以看出,在区间[10,100]上2条曲线符合的比较好。而在区间[1,10]上,尤其是波动区域的附近,2条曲线出入比较大。此外,在区间[0.000 1,1)上2条曲线也有一定的差别。因此,为了达到更好的精度以满足工程需要,决定对得到的9个系数值进行多次优化。以表2中9个数值为初始值,仍然使用可变误差多面体算法进行优化。优化的次数则以拟合的精度为准,一共进行了5次优化,其中以第3次优化后的结果最好。其系数值见
式中:Λ(μi)为原数据值,f(μi)为拟合函数值。Sum的值越小,结果就越好。
经过多次试验后发现,系数为9个时得到的结果最理想:表3。
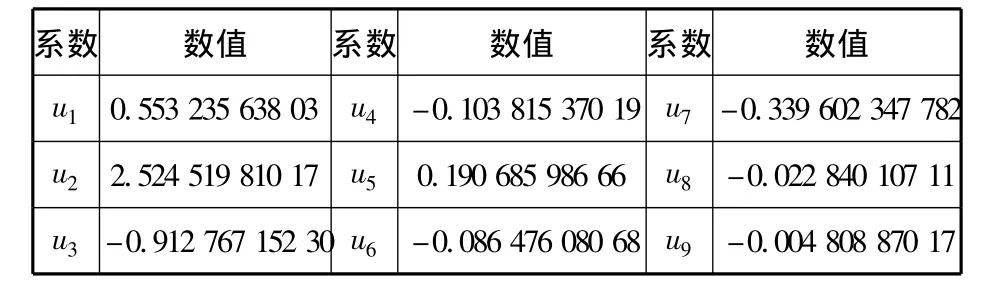
表2 系数值
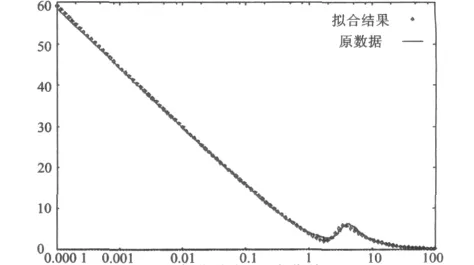
图2 拟合曲线与积分曲线的比较

表3 优化系数值
根据表3所得的优化系数值绘制的曲线,较之未经优化的曲线在精度上有所提高。优化曲线与积分曲线的比较如图3所示。
与最初拟合函数的曲线相比,优化后的曲线无论在原本较好的区间(10,100]上,还是在出入比较大的区间[0.000 1,1)上,甚至在误差最大的波动区域,都符合的比较好了。
因此,最终的拟合函数确定为:
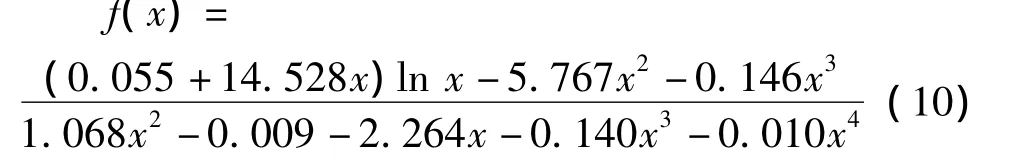
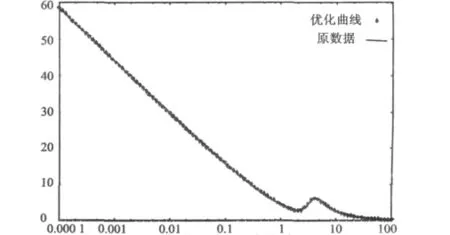
图3 优化曲线与积分曲线的比较
2.2 误差曲线及分析
在前面的工作里,虽然我们已经得到了精度比较好的结果,但是与原数据相比还有一定的误差。出现这些误差的根源,主要是简化、截断和舍入引起的。在最初的积分计算中,采用了式(6)的Hess-Smith近似逼近式,这是模型简化误差的主要来源。而在积分程序以及优化程序的运算过程中,不可避免的又引入了截断误差和舍入误差。因此,式(10)只是一个基本上能满足工程问题要求的近似式,它在每一个计算点的误差可以用对应的曲线表示,如图4所示,图中是对应最优结果的误差曲线。

图4 误差曲线
从图 4 得知,在区间[0.000 1,18]上误差变化比较大,其值为|ε|<0.3;而在区间(18,100]上,误差值|ε|<0.05。这样可以计算出拟合函数的相对误差|η|<6%。这个误差值在所有四次优化结果中是最小的。初始拟合函数的误差与优化后的误差相比是比较大的,而只有第三次优化后的误差亦即最佳拟合函数的误差可以控制在0.3以内。
对于普通的工程计算,这个误差已经可以满足要求。但是,为了可以更加精确,我们希望可以将误差曲线也拟合出来,这样在式(10)后只要减掉误差函数,就可以使拟合函数的误差进一步降低,这在理论上是完全可以实现的。
通过对图4的研究,我们可以初步判断这个要拟合出来的误差函数应该是一个多项式、一个余弦函数和一个指数函数的乘积,其形式应大致为:

当然上式还有很多地方值得商榷,比如说x的次数、项数等,又或其中可能还有其他形式的函数可以替换,这都很有研究价值。我们只在式(11)的基础上,使用可变误差多面体法,得到了一个精度很一般的结果,其系数值见表4。

表4 系数值
由表4中的数值绘制出的误差拟合函数的曲线如图5所示。从图5中可以看出,精度是比较差的,但是拟合曲线的大体趋势是对的,这说明拟合函数的形式基本正确。

图5 拟合曲线与误差曲线的比较
3 三维脉动源格林函数的简化

在靠近自由表面的位置z=ζ=0,则可得如下形式:
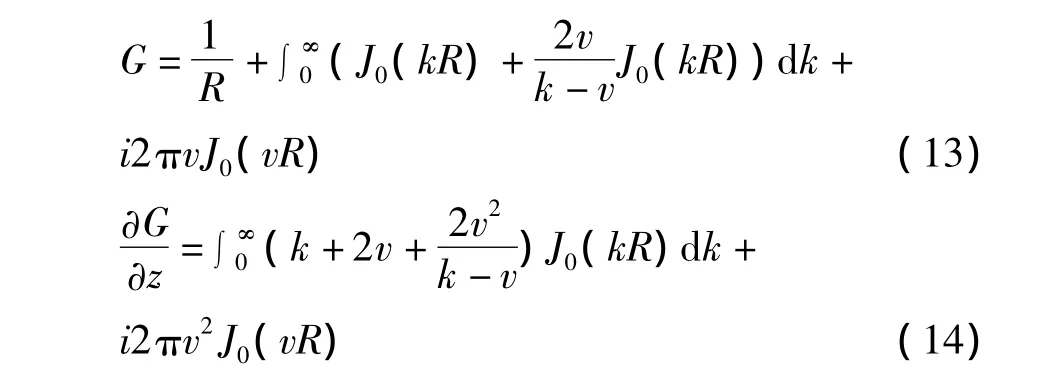

4 结论
为了简化计算,本文提出了拟和简单函数的思想。采用可变误差多面体算法来拟和形式复杂的函数,将一个表示三维脉动源的格林函数简化为形式简单计算方便的复合函数。在满足精度要求的前提下,大大减少了计算量。尽管原函数的拟和曲线比较理想,但误差曲线的拟和还有 一些不足之处。不过这项探索性的研究说明这种思想是可行的,为今后的工作提供了可以使用的简单函数。
[1] 宗智,黄鼎良.三维移动脉动源速度势的数值研究[J].水动力学研究与进展,1991,(6):55-63.
[2] 卢晓平,叶恒奎,张纬康,等.Haskind源格林函数的奇异性研究与数值积分方法[J].水动力学研究与进展,1999,14(4):444-452.
[3] XU Y,DONG W C.Study on characteristics of 3-D translating-pulsating source Green Function of deep-water Havelock form and its fast integration method[J].China Ocean Engineering,2011,25(3):365-380.
[4] YAO X L,SUN S L,WANG S P,YANG S T.The research on the highly efficient calculation method of 3-D frequency-domain Green function[J].Journal of Marine Science and Application,2009,8:196-203.
[5] 戴愚志,余建星,郭海涛.时域有限水深格林函数及其导数的数值计算[J].船舶力学,2006,10(1):15-21.
[6] 刘昌凤,勾莹,滕斌.时域格林函数卷积的新算法[J].水动力学研究与进展,2010,25(4):524-533.
[7] 纪刚,张纬康,卢晓平.无航速具有自由液面的三维脉动源Green函数的数值积分方法[J].海军工程大学学报,2004,16(6):89-92.
[8]陈崧,赵留平,侯磊.无航速具有自由液面的三维Green脉动源函数的数值积分方法[J].中国舰船研究,2006,1(2):50-52.

