EMD在循环谱检测中的应用研究

高立龙，王新晴，蒋文峰

（解放军理工大学工程兵工程学院，南京 白下 210007）

循环平稳信号分析方法作为一个崭新的信号处理工具，利用信号本身的周期时变特征来揭示分析对象的特征信息，具有较强的解调能力。最近几年，循环平稳理论已经成为机械状态监测和故障诊断领域的热门研究对象，并取得了不少的成果。在工程实际中大量的循环平稳信号，如汽车发动机的振动信号、汽车传动轴运转振动信号等均具有循环平稳特性。

根据循环谱分析理论我们知道，循环自相关函数对于单分量信号具有较好的解调能力，但对多分量信号进行循环自相关函数分析时会引入交叉项，出现虚假频率，影响能量的分布，难以判断信号中的真实成分。

本文利用EMD方法将多分量信号分解为物理意义明确的一系列本征模式函数（IMF）之和，对这些IMF分量进行循环自相关分析，然后再将分析结果相加，得到循环自相关函数的累加图，可消除交叉项干扰。

1 循环自相关函数对多调制信号解调能力分析

设信号 x（t）包含两个加性调幅信号，即：x（t）=x1（t）+x2（t）

式中各参数的意义与上面相同。其时变自相关为：

则根据循环自相关函数的定义【2】，可得：

因此信号 x（t）的循环自相关函数 Rxα（τ）由四部分组成，即 x1（t）的循环自相关函数 Rx1α（τ）、x2（t）的循环自相关函数Rx2α（τ）、x1（t）和的循环互相关函数 Rx1x2α（τ）、Rx2x1α（τ）。

当上述两个加性调幅信号 x1（t）和 x2（t）之间严格独立时，两者之间的循环互相关函数 Rx1x2α（τ）、Rx2x1α（τ）为零，此时 Rxα（τ）=Rx1α（τ）+Rx2α（τ）。 然而由于 x1（t）和 x2（t）之间的相关性事先并不能获知，一般情况下两者并不严格独立，因此两者之间的循环互相关函数 Rx1x2α（τ）、Rx2x1α（τ）一般不为零，故 Rxα（τ）≠Rx1α（τ）+Rx2α（τ），此时就产生了交叉干扰项 Rx1x2α（τ）+Rx2x1α（τ）。

产生交叉项的原因在于，循环自相关函数是二次型变换，当信号包含多个加性或耦合的调制信号时，对其求解循环自相关函数时会不可避免地产生交叉项。交叉项的存在影响了正常的信号分布，且引入了难以解释的各种干扰频率，这就为信号的进一步分析带来了困难。

为了解决这个问题，本文提出基于经验模式分解（EMD）处理方法。根据经验模式分解（EMD）的思想，我们可以自适应地将多分量信号分解成一系列本征模式函数（IMF）分量之和，然后对各IMF分量进行分析。

基于经验模式（EMD）分解消除循环自相关中的交叉项的算法步骤为：

（1）将信号进行EMD分解，得到一系列的本征模式函数（IMF）分量。

（2）计算各个IMF分量的循环自相关函数；

（3）将计算得到的各IMF分量的循环自相关函数的结果进行累加，就可以避免交叉项的产生，得到原信号的循环自相关函数。

下面分别对单分量和多分量信号进行仿真分析，验证循环自相关函数的解调能力，考察EMD算法抑制交叉项的能力。

2 信号仿真实例

例1.设信号x（t）包含有两个加性调幅信号，即：

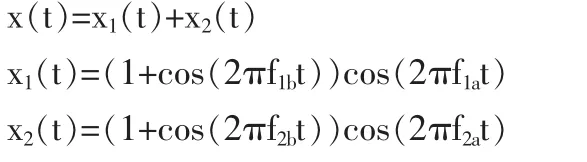
式中，f1a=100Hz，f1b=13Hz，f2a=250Hz，f2b=30Hz。 采样频率fs=2000Hz，采样点数 N=2048。

图1为信号 x（t）的时域图，图 2为 x（t）的时延为 0时的循环自相关函数。从图2可以看出，在低频区域分离出调制频率及其二倍频，高频区域分离出两个载波频率的二倍频及与调制频率相关的边频。在图2中除了分离出的与信号载波频率和调制频率相关的信息外，还出现了大量的难以解释的频率成分，例如出现了150Hz、350Hz为中心的频带，显然是对信号计算循环自相关函数时引入的交叉项，它们的出现对判断信号的载波频率和调制频率造成了严重的干扰。

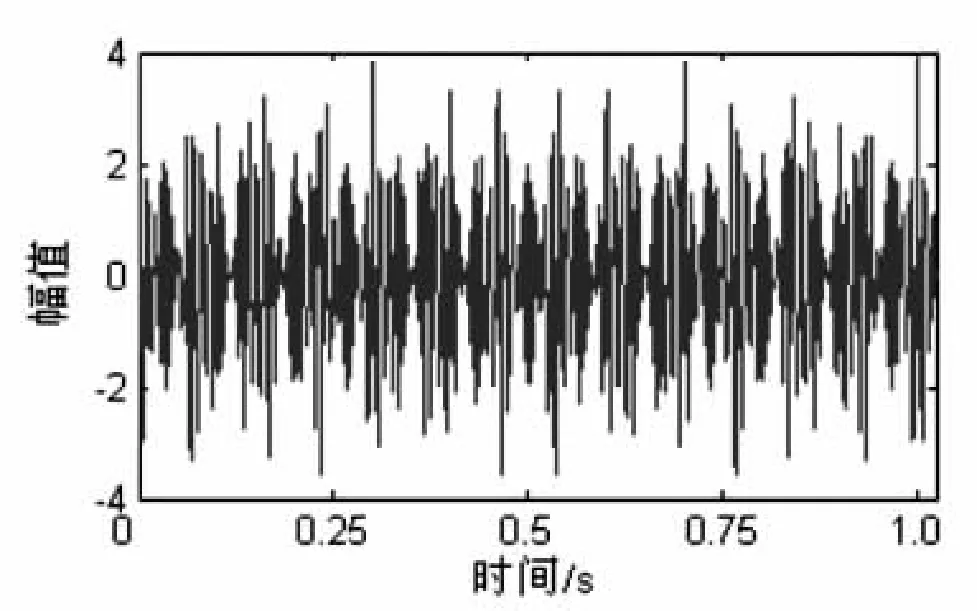
图1 信号时域图

图2 信号的时延为0时的循环自相关函数图

现对例2中的多分量信号进行EMD分解，对各IMF分量进行循环自相关分析，求出循环自相关函数累加图，并进行比较。

信号经过EMD分解后可以得到2个IMF分量和1个残余分量，图3所示的是第一个IMF分量IMF1的时域图，图4显示的是第二个IMF分量IMF2的时域图，图5所示的是分解后的残余分量的时域波形图。分别对IMF1、IMF2分量进行循环自相关分析，得到IMF1和IMF2的循环自相关函数值，如图6、图7所示，在图6中循环频率包括0Hz、±30Hz、±60Hz、±500Hz、±(500±300)Hz、±(500±600)Hz，低频部分表示信号 x1（t）的调制频率及其 2 倍频，高频部分表示 x1（t）的载波频率的2倍频以及以此为中心，与调制频率相关的边频带。图7中循环频率包括 0Hz、±13Hz、±26Hz、±200Hz、±(200±13)Hz、±(200±26)Hz，低频部分表示信号 x2（t）的调制频率及其 2 倍频，高频部分表示x2（t）的载波频率的2倍频以及以此为中心，与调制频率相关的边频带。图6、图7表明经过信号EMD分解后得到的IMF1分量和IMF2分量就对应于信号x1（t）和x2（t）。图8为IMF1和IMF2分量的循环自相关函数值的累计值，对比图2和图8可以发现，多分量信号经过EMD分解后的循环自相关函数值没有出现交叉项，这也就说明EMD分解方法能够有效地去除循环自相关函数中的交叉项问题。

图3 IMF1分量的时域图

图4 IMF2分量的时域图

图5 残余分量的时域图

图6 IMF1分量的循环自相关函数图

图7 IMF2分量的循环自相关函数图

图8 IMF1、IMF2循环自相关函数累加图

3 结语

仿真实例表明，基于经验模式分解（EMD）的方法能够有效的解决循环自相关函数在多分量信号解调中的缺陷，从根本上解决了交叉项干扰的问题。

[1]JIANG Ming,Chen Jin.Comparison between Cyclic Statistics and Envelope Demodulation.Journal of Shanghai University(English Edition)，2004，8(2):193-198.

[2]陈进，姜鸣.高阶循环统计量理论在机械故障诊断中的应用[J].振动工程学报，2001，（2）.

[3]李力，屈梁生.二阶循环统计量在机械故障诊断中的应用[J].西安交通大学学报，2002，（9）.