基于均生函数模型的高温预测

郎许锋，何月顺

（东华理工大学信息工程学院，江西 抚州 344000）

1 概述

高温气候已成为人们健康、生命安全和经济安全的一个重要影响因素，近些年高温事件逐渐呈现高强度和频率的趋势。而我国尚未有比较有效和专业的中长期预测平台，本文以国家气候中心的高温热浪预报预警系统作为背景，介绍了从气象监控数据中获取原始数据，采用均生函数模型预测高温出现情况，并通过Arc GIS生成最终的图形产品。

由于气象数据按照时间序列具有明显的震荡特征，传统的灰度、指数平滑模型在这方面的预测效果并不理想。均生函数模型借助多元分析的手段，分析原始数据序列，构建一组周期函数，经过分析元数据和该周期函数后，建立相应的统计模型，通过此模型可以对历史资料进行拟合或者对未来趋势的预测，从而很好的应用于解决时间序列预测问题，它既可以作多步预测，又可以较好地预测极值，因此，本文利用均生函数统计方法与周期分析原理，实现对每年4~9月未来1个月中国范围内大于或等于35℃高温天气预测。

2 气象检测数据获取

通过Fortran函数调用，从国家气象信息中心MDSS实时库中获取常规地面天气要素，首先以文本文件的形式，分类存放在本系统自治的存储设备中，再对各种文本文件解析入库。从文件库和数据库中获取相应的气象数据，根据用户定制的任务生成相应的数据产品，如各测站周降水资料、各测站月最高（最低）温度等ASCII码文件，提供给产品生成模块使用。本模块用到各气象观测站点每日报告中的日最高气温。具体逻辑结构如图1所示。

图1 高温预测数据处理逻辑图

3 均生函数模型介绍

均生函数模型由时间序列按不同的时间间隔计算均值，生成一组同期函数，然后用原时间序列与这组函数建立回归预测方程。

其中，i=1，2，……k，k；k=1，2，……，M；式中：nk=INT（N/K）；M=INT（N/2）或 INT（N/3），INT 表示取整。 对（i）作同期性延拓,则可得到其外延序列:fk=，称 fk(t)为均生函数的延拓序列。建立fk(t)与观测原序列间的一元回归：x，其中 q≤M。

利用均生函数外延值，可对原序列做多步预测。

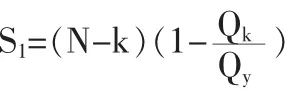
4 图像产品生成和检验

建立全国轮廓图层，其中包含各个地面气象观测站点信息。在得到客户端（浏览器端）请求后，根据客户所要求的时间范围，通过上述均生函数模型计算各站点的日最高气温。利用Arc GIS生成范围专题图的功能，将温度大于等于35℃的地区连接成区域，最终展示给客户端。如图2、图3所示。

图2 2007年8月23日未来24小时预测图

考虑到建模数据的时间序列较短，可采用交叉检验的方法，用逐次预测值与相应预测值的相关系数反映该方法的模拟效果。首先选择一个年份的日最高气温作为观测样本，用其余N-1个样本建立预测模型，估计所选择的观测样本值，依此重复N次，得到N个样本的N个估计值。分别计算各次预测的平均误差和最后的标准差，来验证系统预测的准确性。

图3 2007年8月23日未来24小时观测图

5 结语

通过均生函数模型，可以获得多步或较长时间的温度预测结果，并且具有较高的预测准确率和稳定性。采用Arc GIS的方式生成图像，不仅可以做到按客户需求返回实时、个性化的产品，而且在服务器的运行效率和与其他程序的交互功能上也有很好的效果。

[1]曹鸿兴，魏风英，刘长生.多步预测的降水时序模型[J].应用气象学报，1993，4（2）：198-204.

[2]许丽玲，侯维峰，刘璐.均生函数模型在气温和降水预测中的应用[J].黑龙江气象，2007，（4）.

[3]董秀丽，王贵平，哈立宇.用均生函数模型做赤峰夏季温度和降水气候预测试验[J].内蒙古气象，2008，（1）.

[4]唐毓勇，蒋国兴，周礼杏，等.均生函数预报模型的改进实验[J].气象，2007，（9）.

[5]孙映宏.基于均生函数模型的杭州市年降雨量预测[J].水电能源科学，2009，（2）.

[6]袁本荷.利用均生函数预测模型作降水预报[J].四川气象，2005，（3）.

[7]杨瑞峰，刘庆民.均生函数模型在长期天气预报中的应用[J].河南气象，2004，（1）.

[8]李建平，聂爱香.基于Arc Engine的县级GIS应用系统的开发[J].地理空间信息，2006，（5）.

[9]匡昭敏，陈超泉，黄永璘，何立，莫伟华.基于RS和GIS的生态环境监测评估应用系统[J].计算机工程，2008，（8）.

[10]兰进京，刘凯，郑逢杰.基于组件化GIS技术的立体灾害地质图生成软件研究[J].科技创业月刊，2011，（7）.

[11]石伟伟.GIS 服务气象防灾减灾[J].数字通信世界，2011，（8）.

[12]王洪源，张武，金莉莉.基于GIS的城乡电网管理系统[J].微计算机信息，2005，（11）.

[13]陶雪梅.基于GIS的气象资料查询系统的设计与开发[J].微计算机信息，2007，（22）.

[14]沙莎，曹芸，朱晓晨.基于GIS的气象灾害评估系统——干旱评估模块的研究[J].科技信息，2009，（23）.