发生不连续屈服的钛合金高温变形研究进展
王哲君,强洪夫,王学仁
(西安高新技术研究所601室,西安 710025)
发生不连续屈服的钛合金高温变形研究进展
王哲君,强洪夫,王学仁
(西安高新技术研究所601室,西安 710025)
不连续屈服行为是近α、β钛合金高温变形过程中出现的一种重要现象,对钛合金高温变形的力学特性有重要的影响,引起了材料研究者越来越广泛的关注。综合目前发生不连续屈服的钛合金高温变形研究现状,介绍了下屈服点前、后的流动曲线特性;分析了影响不连续屈服的主要因素、不连续屈服发生的相关机理;探讨了发生不连续屈服的钛合金高温变形机制和考虑不连续屈服现象时钛合金高温变形的本构模型构建;并在此基础上提出了当前研究中存在的不足和值得进一步研究的内容。
不连续屈服;钛合金;高温变形;变形机理;本构模型
Abstract:The discontinuous yielding behavior is one of the important phenomenas for near α and β titanium alloys during hot deformation. It has the important effect on the mechanical behavior of titanium alloys during hot deformation,and there has been a growing interest on this phenomenon. With a view to the current researches of high temperature deformation of titanium alloys with discontinuous yielding, the characteristics of flow stress curves before and after the lower yield point were introduced. The dominating influencing factors and theoretic mechanism on the discontinuous yielding were analyzed. The deformation mechanism of titanium alloys with discontinuous yielding during hot deformation was discussed as well as the methods to develop the constitutive model. At last the current shortage and future research contents were also proposed.
Key words:discontinuous yielding; titanium alloy; hot deformation; deformation mechanism; constitutive model
钛合金作为一种在较高温度下具有比强度高、断裂韧性高、耐高温和抗腐蚀性好等特别优异性能的合金材料,在航空航天等领域被广泛应用。金属材料经常要在高温环境中承受变形,在变形的同时内部微观组织会发生变化,最终影响材料的力学性能,因此,研究和探索钛合金的高温变形有重要的工程应用和学术价值[1]。钛合金高温变形的主要影响机制是动态回复和动态再结晶,而对于近α、β钛合金在高温变形时还经常显现出类似于退火钢、部分BCC金属变形过程中出现的不连续屈服现象或称为屈服点下降现象[2]。不连续屈服行为对材料变形初期的力学性能有重要的影响,国内外的材料研究者虽然认识到了金属变形过程中尤其是温度范围在β相变点附近钛合金高温变形时的不连续屈服现象,并尝试运用各种理论对其进行有效的物理解释[2−5],部分研究者也在通过构建本构模型来描述发生这种现象的合金高温变形和进行有限元模拟[6−10],但由于影响不连续屈服行为因素的复杂性和钛合金高温变形本身的复杂性,至今没有形成系统有效的理论来解释钛合金高温变形过程中出现的不连续屈服现象。一些发生不连续屈服的钛合金高温变形
本文作者在介绍国内外材料研究者对于发生不连续屈服的钛合金高温变形研究的基础上,对其流动曲线特性、影响不连续屈服的主要因素、当前构建本构模型的方法等进行有效的归纳和分析,指出研究中存在的不足及需要进一步研究的内容。
1 发生不连续屈服的钛合金高温变形流动曲线特性
1.1 流动曲线的基本特征
1) 钛合金在高温变形条件发生不连续屈服现象时,流动曲线上最明显的标志是:在变形初期的低应变区有一个尖锐的峰值应力,然后应力值急剧下降,或者出现明显的上(σUY)、下(σLY)屈服点[2],流动曲线呈现下凹趋势;
2) 钛合金高温不连续屈服流动曲线同软钢等变形过程中的不连续屈服流动曲线(见图 1)较为明显的区别是:在下屈服点之后不出现吕德应变或屈服平台,这种屈服现象也被HAHN等[6]称为均匀屈服;
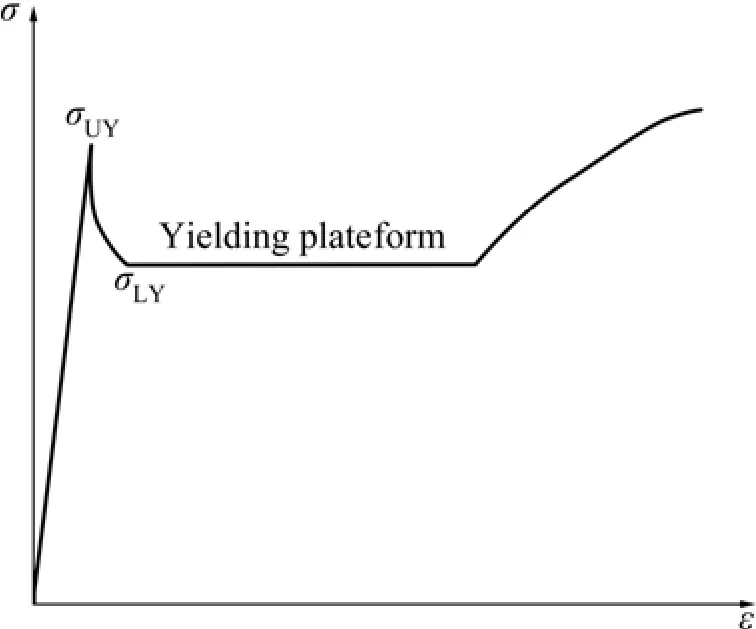
图1 低碳钢不连续屈服的示意应力—应变曲线Fig.1 Schematic illustration of stress—strain responses of mild steel showing discontinuous yielding phenomenon
3) 变形温度和应变速率越高,不连续屈服现象越明显(见图2和3),而且上下屈服点之间的应力差值越大(见图4)。同时变形温度越低、应变速率越高,发生不连续屈服现象时上屈服点的应力值越高。不连续屈服现象多发生在应变速率值较高的区间和β相变点附近或高于β相变点的温度区间,但这种高的应变速率是相对的,随着钛合金种类的不同而发生变化。

图2 Beta CEZ在β相变点以上的流变曲线[11]Fig.2 Flow curves of Beta CEZ above β transus temperature[11]
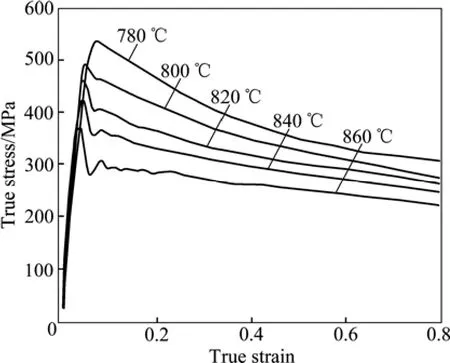
图3 Ti-17应变速率为10 s−1、变形量60%的流变曲线[12]Fig.3 Flow curves of Ti-17 at strain rate of 10 s−1and 60%height reduction[12]
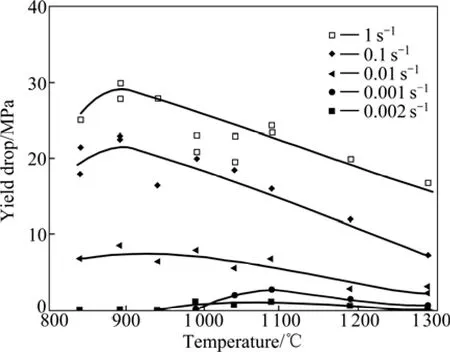
图4 Ti-6.8Mo-4.5F-1.5Al屈服下降随温度和应变速率的变化[13]Fig.4 Magnitude of yield drop in Ti-6.8Mo-4.5F-1.5Al as function of temperature and strain rate[13]
1.2 下屈服点后的流动曲线特性
钛合金在高温变形条件下发生不连续屈服现象时,在下屈服点之前,流动曲线均显现出类似于 1.1节的变形特性,但在下屈服点之后,随着应变量的增加,流动曲线呈现不同的特性:
1) 随着应变量的增加,无硬化阶段产生,流动曲线呈现稳态流动特性(见图2);
2) 随着应变量的增加,无硬化阶段产生,流动曲线呈现持续软化流动特性(见图5);
3) 随着应变量的增加,在较小的应变范围有轻微的应变硬化阶段出现,然后流动曲线呈现稳态流动特性(见图6);
4) 随着应变量的增加,在较小的应变范围有轻微的应变硬化阶段出现,然后应力值不断下降,呈现持续软化特性(见图3)。
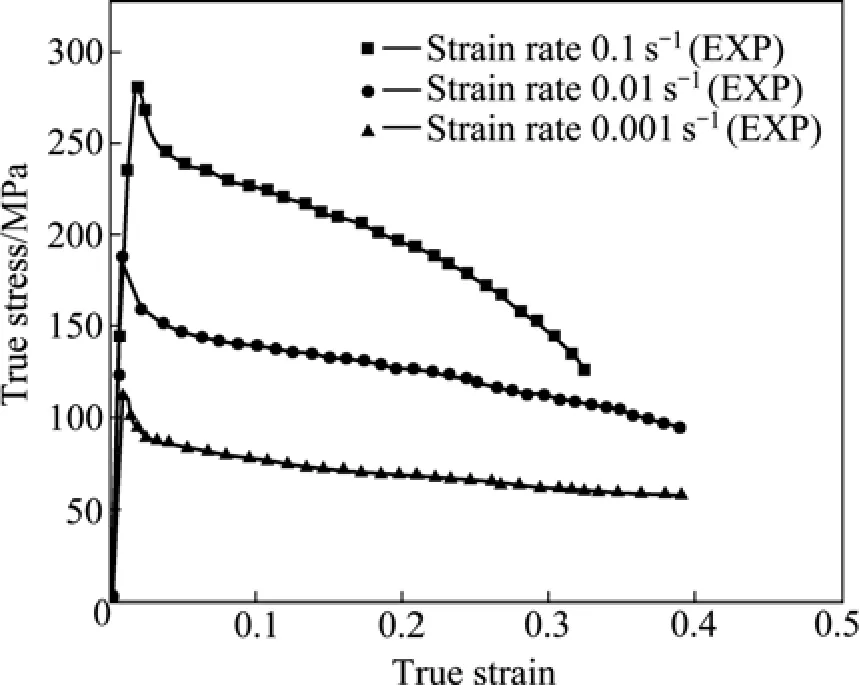
图5 Ti-20V-4Al-Sn在700 ℃下的应力—应变曲线[14]Fig.5 Stress—strain curves of Ti-20V-4Al-Sn at 700 ℃[14]
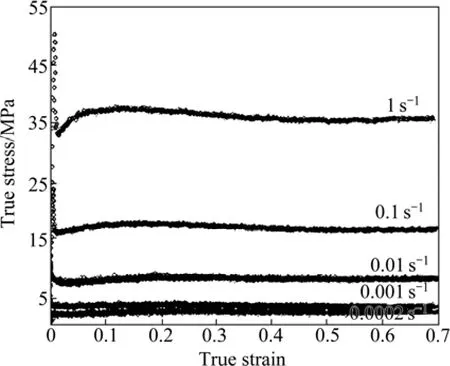
图6 Ti-6.8Mo-4.5F-1.5Al在1 290 ℃下的应力—应变曲线[13]Fig.6 Stress—strain curves of Ti-6.8Mo-4.5F-1.5Al at 1 290 ℃[13]
而普通软钢等金属变形过程中发生不连续屈服现象时,流动曲线大多在屈服平台之后呈现明显的应变硬化特性,几乎没有流动软化现象出现(见图1)。
变形曲线特性在很大程度上反映了材料变形过程中内部微观组织的变化情况。而钛合金高温变形发生不连续屈服时,无论是在呈现明显上下屈服点的变形初期还是下屈服点之后的变形阶段,在流动曲线特性上都与普通软钢等金属有较明显的区别。目前针对钛合金高温变形不连续屈服下屈服点之前的变形特性,众多研究者已对其进行了较多的研究并取得了较为一致性的结论;针对下屈服点之后的流动曲线特性1)和特性2),也有研究者对其进行研究。上述研究的相关内容将在后文中进行阐述。而对于特性3)和特性4),只是在压缩试验的流动曲线上被大多数研究者所观察到,还缺乏相应的物理解释和本构模型。要较好地描述发生不连续屈服的钛合金高温变形,必须对变形过程中的变形机制、影响因素等进行有效的研究,探明相关机理。同时,钛合金发生不连续屈服的复杂高温变形特性要求研究者根据具体的材料特性、具体的变形条件,结合实验手段进行进一步的研究。
2 影响钛合金高温变形不连续屈服的主要因素
钛合金高温变形的流动曲线显示:变形温度和应变速率对不连续屈服的发生有重要的影响。但1.2节的分析表明:影响钛合金高温变形不连续屈服的主要因素不仅仅局限于变形温度和应变速率。本节主要对其它因素进行简要的介绍。
1) 晶粒尺寸的影响。LONG和RACK[15]通过研究β钛合金Ti3Al(Nb, Mo)高温变形时发生的不连续屈服现象,发现流动应力的下降幅度随着晶粒尺寸的增加而减小。BALASUBRAHMANYAM和PRASAI[16]对于Ti-10V-4.5Fe-1.5Al的高温变形特性研究有相同的结论。
2) 溶解度的影响。VUAYSHANKAR和ANKEM[17]在β钛合金Ti-Mn高温拉伸变形过程中,发现在给定的变形温度和应变速率下,流动应力值和应力下降幅度随着Mn 固溶元素的增加而增加。PHILIPPART和RACK[13]的研究同样发现屈服现象是与材料成分相关的,屈服点处流动应力值随固溶程度的变化情况和VUAYSHANKAR和 ANKEM 的研究[17]一致。WANJARA等[18]在研究IMI834高温变形时,同样把屈服下降的影响归结为较高的固溶程度和合金中大量固溶尺寸较大的碳原子。
3) 合金成分的影响。不连续屈服发生于 Ti-14.8V、Ti-13Cr-11V-3Al、Ti-5Al-2Sn-2Cr-4Mo-4Zr-1Fe钛合金中,而在 Ti-5Al-2.5Sn高温变形时却没有发现[2],说明不连续屈服现象与钛合金的具体成分有关。VUAYSHANKAR和 ANKEM[17]通过比较 β钛合金Ti-Mn和Ti-V的高温拉伸变形曲线发现,在给定的变形温度和应变速率下,Ti-Mn较Ti-V具有更高的流动应力和较大的应力下降幅度。PHILIPPART和RACK的研究[13]同样指出钛合金中所含元素的类型对于β钛合金的高温不连续屈服有重要的影响,随着所含元素原子与钛元素原子尺寸差别的增大,屈服下降的程度会增加。WANG等[19]认为钛合金高温变形时的不连续屈服现象还与β相的含量有关。
4) 峰值应力前的预变形影响。VUAYSHANKAR和ANKEM[17]在β钛合金Ti-Mn的高温拉伸变形过程中发现,钛合金在较小的预加应变下变形时不连续屈服现象更为明显,流动应力下降幅度更大。
5) 退火温度的影响。VUAYSHANKA和ANKEM[17]在β钛合金Ti-Mn和Ti-V的高温拉伸变形曲线中发现,在β相温度区间,随着退火温度的提高,材料的不连续屈服现象更明显,上屈服点的应力值更高,上下屈服点的应力差值更大。
3 钛合金高温变形不连续屈服的物理解释
3.1 描述钛合金高温变形不连续屈服的基本理论
由于钛合金高温变形特性的复杂性,关于其高温不连续屈服现象,至今仍没有统一的理论解释。可能的变形机理包括柯氏气团的钉扎原理、高温下大量位错源开动导致的位错增殖理论和金属材料的高温软化理论,主要是动态再结晶理论。
3.1.1 柯氏气团的钉扎理论
基于COTTELL和BILBY的理论[20],认为在开始变形之前,固溶原子聚集在位错线周围,形成“柯氏”气团,合金中虽有大量位错,但大都被钉扎住,需要较大应力才能使它脱钉而开始运动,因此出现了上屈服点。一旦所加外力达到上屈服点,位错便摆脱气团的钉扎发生滑移,造成大量可动位错的产生,此时不需要很大的应力即可运动,因此应力下降而出现下屈服点,产生不连续屈服现象。JONAS等[21]发现β Zr-Nb合金的不连续屈服现象随固溶元素含量和预加热时间的增加而增加,使得该原理在一定程度上得到了有力的证明。但是,该理论不能很好地解释变形初期的屈服点急剧下降现象以及变形温度和应变速率对钛合金高温变形不连续屈服现象的影响规律。而且ANKEM等[22]、SRINIVASAN和WEISS[23]、WEISS和 SEMIATIN[2]的研究也表明钛合金高温变形过程中出现的不连续屈服现象不能用柯氏气团的钉扎原理进行有效解释。
3.1.2 位错增殖理论
该解释基于JOHNSTON和GILMAN对LiF的变形特征的研究[24],认为在开始变形之前,晶体中可动位错密度很低;一旦塑性变形开始,可动位错便大量增殖,最终影响合金的流动应力值。但是在峰值应力的出现和随后应力急剧下降的解释上存在区别。
古人云:腹有诗书,其德自谦;腹有诗书,其身自正;腹有诗书,其志自坚。说的是读书不仅可以增智、博采、长才,还可以修身、养性、怡情。而我读书,仅是工作之需和心灵之需,是为让自己不再心慌和心荒,尽好一个小学语文教育工作者的责任。如果要用一句话来概括我这十多年的读书心得,那就是:为“需”而读可养心。
1) 第一种解释是依据位错运动的理论,认为晶体材料塑性变形的速度νε与晶体材料中可动位错的密度 ρm、位错运动速度 ν以及位错的柏氏矢量 b成正比[25]:

位错运动速度,又决定于它所承受的应力τ[24]:

式中:m是材料本身的应力敏感系数,它是一定材料中位错运动速度对应力敏感性高低的量度。τ0是使得位错得到单位运动速度所需的应力。
在开始变形之前,晶体中可动位错密度很低,因此材料开始变形的速度νm是很低的,但是接近加工夹具的部位,被迫以一定的速度随夹具移动,产生较大的应变速度νs,迫使位错运动速度ν增大。由式(2)可知,要使位错运动速度ν增大,就需要增加外力,以提高作用在位错上的应力 τ。因此塑性变形开始,所需应力是较高的,出现明显的上屈服点。
一旦塑性变形开始,位错就会迅速增殖,使可动位错的密度ρm迅速增大,在宏观应变速率νs一定的条件下,由式(1)可知,使位错运动所需要的应力 τ,也就会迅速降低下来,出现下屈服点,呈现不连续屈服现象。该理论解释多用来构建反映不连续屈服现象的本构模型,具体内容将在后续章节进行阐述。
2) 第二种解释认为[26]:塑性变形开始后,由于晶界的阻碍作用,使得产生的大量位错发生塞积,导致流动应力急剧升高,当位错密度达到某一临界值时,β相中的动态回复突然增加,使得塞积的位错通过攀移等方式进入晶界内部,使得大量异号位错相互抵消,位错塞积减缓,从而导致流动应力大幅下降,出现不连续屈服现象。PHILIPPART和 RACK[13]及赖运金等[12]分别在Ti-6.8Mo-4.5Fe-1.5Al和Ti17的TEM照片中发现:合金在一定应变速率下变形后,晶界处有位错塞积现象。
3.1.3 动态再结晶理论
部分研究者仍认为材料在高温变形过程中,峰值应力后出现的应力急剧下降现象是由于动态再结晶机制的出现,使得位错密度大量降低,完全消除了应变硬化的作用[27−28]。但是这种理论无法解释钛合金高温变形过程中低应变速率下(值在0.01 s−1附近)变形初期出现的不连续屈服现象。图2和5所示钛合金均在应变速率为 0.01 s−1附近较低的应变速率下发生了明显的不连续屈服现象。因为在动态再结晶理论中,低应变速率下,合金在较小的应变下就达到发生动态再结晶的临界应变,降低了位错的积累,不利于不连续屈服现象的发生[29]。低应变速率下发生动态再结晶时,由于在再结晶形核长大期间还进行着塑性变形,曲线呈现波浪形,或称为不连续再结晶现象[29],虽然在流动曲线特征上与不连续屈服有类似之处,但在变形后期流动曲线基本都是呈现稳态流动,几乎不出现软化现象(见图7)。所以本文作者认为,动态再结晶机制是不适合解释钛合金高温变形过程中出现的不连续屈服现象。
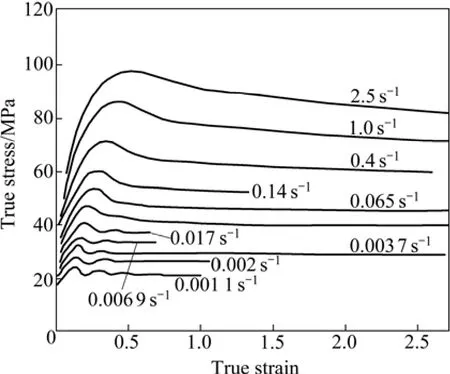
图7 0.25%碳钢在温度为1 100 ℃应变速率为1.1×10−3~2.5 s−1下的应力—应变曲线[30]Fig.7 True stress—true strain curves for 0.25%-carbon steel obtained at 1 100 ℃ and strain rates between 1.1×10−3and 2.5 s−1[30]
3.2 发生不连续屈服的前提条件
1) 较低的可动位错密度。3.1节关于不连续屈服的基本理论表明:虽然3种理论在开始变形前,导致可动位错密度较低的因素不同、塑性变形发生后出现不连续屈服的原因不同,但是都要求开始变形前,材料要具有较低的可动位错密度,这一点也是所有研究不连续屈服现象者的共识;
2) 塑性变形中可动位错能够迅速增殖。3.1节的3种理论,都要求在塑性变形开始后位错能够迅速增殖,只有具有较高的可动位错密度,才能引发流动应力的下降。而且ANKEM等[22]确实在钛合金变形不同温度下的位错结构中,发现了引发大量位错突然增殖的位错源;
3) 应力敏感系数m要小。如式(2)可知,m值越大,差值越小,因为m值很大时,应力τ稍微下降,位错速度ν就降低很大,即可满足保持宏观应变速率不变的要求[25]。在WANG等[32]对Ti-20V-4Al-1Sn钛合金高温变形条件下不连续屈服的计算中,应力敏感系数m的值低于6。这也验证了钛合金高温变形过程中要出现明显的不连续屈服,就必须具有较低的应力敏感系数。
3.3 影响钛合金高温变形不连续屈服因素的物理解
释
1) 温度的影响机理。位错攀移伴随着物质的迁移,需要扩散实现。而温度是扩散的驱动力,温度越高,扩散越容易进行,位错攀移越容易,不连续屈服现象越明显。同时基于3.1.2中的第二种解释,可动位错的突然增殖本质上是动态回复突然加剧引起的,因而温度越高,动态回复的驱动力越大,不连续屈服现象越明显。而温度升高,原子的平均动能增大,材料的热激活作用增强,又减小了晶体发生滑移的临界分切应力,有利于位错运动以及晶界的滑移,最终导致金属高温变形的变形抗力减小,不连续屈服发生时的峰值应力相应的减小[33];
2) 应变速率的影响机理。发生不连续屈服的前提条件是位错密度的积累,而较高的应变速率是产生位错的来源。所以应变速率越高,不连续屈服现象越明显[33]。同时应变速率增大,塑性变形不能在变形体内充分地扩展和完成,而弹性变形仅是原子离开其平衡位置,增大或缩小其原子间距,因此扩展速度很大,这样就会更多的表现为弹性变形。根据胡克定律,弹性变形量越大,应力就越大,即真实流动应力越大[34],不连续屈服现象发生时的峰值应力相应的增大。第三,增加应变速率,由于没有足够的时间进行回复等机制,位错的积累导致较高的局部应力集中,同样在不连续屈服发生时引发较高的峰值应力[34];
3) 晶粒尺寸的影响机理。由于位错是从晶界处出发的,是与晶界尺寸相关的,因此,晶粒尺寸越小,晶界就越多,晶界对于位错的强化作用就越明显,流动应力增加的也就越大,位错运动后流动应力的下降也就越大,发生不连续屈服现象就越明显[17];
4) 溶解度的影响机理。材料中固溶程度的变化会引发热平衡溶度的变化,而平衡溶度的变化又会导致应力下降程度的变化。当变形温度一定时,随着固溶元素的增加,平衡浓度得到提高,最终引起流动应力和应力下降幅度的增大[17];
5) 合金成分的影响机理。SRINIVASAN 和WELSS[23]认为,合金成分影响溶质原子与位错的弹性交互作用。固溶元素类型对钛合金高温不连续屈服的影响主要是由于钛元素原子尺寸与固溶元素原子尺寸差别越大,会引发位错与固溶原子之间更强的相互作用,而这种更强的相互作用,会促使不连续屈服发生时具有更高的峰值应力和较大的应力下降幅度[18]。WANG等[35]认为β相含量的增加对变形机制的影响是由于高温变形时,晶界强度降低,点阵内部扩散起主要作用,晶界滑动由晶粒内部位错滑移来协调。而随温度升高,参与变形的β相含量增加,由于晶体滑移系统的不确定性,增加了两相之间变形抗力的不一致,变形过程中互相限制和阻碍;
6) 预变形的影响机理。不连续屈服发生的一个很重要的前提条件是要具有很低的可动位错密度。而根据ARSENAULT、VUAYSHANKAR和AKKEM[17]的研究,认为峰值应力前的预变形改变了材料中的可动位错密度,可动位错密度的变化会直接影响峰值应力和应力的下降幅度。较大的预变形,引发材料中可动位错密度的提高,而变形前较高的可动位错密度会导致较低的峰值应力和较小的应力下降幅度;
7) 退火温度的影响机理。较高的退火温度会引发材料中较低的可动位错密度,而较低的可动位错密度会导致较为明显的不连续屈服现象[17]。
总之,本节关于影响钛合金高温变形不连续屈服因素的物理解释,是在对大多数钛合金高温变形特性研究基础上的总结和归纳。由于钛合金自身所含元素的多样性以及变形机理的复杂性,对于钛合金高温变形不连续屈服影响因素的物理解释要依据具体的变形条件、具体的合金特性进行。部分研究者的研究发现,一些钛合金高温变形的不连续屈服特性就有别于 3.3节的讨论,需要给予特别关注。
1) 太高或太低的应变速率均不利于不连续屈服的发生,应变速率的大小因合金成分而异。张树志[36]在研究 Ti-46Al-2Cr-4Nb-0.3Y 高温变形以及BALA-SUBRAHMANYAM 和 PRASAD[37]在研究Ti-10V-2Fe- 3Al合金高温变形过程中均得出与此相同的结论。这是由于在较高的应变速率下,可能由于某种机制的影响,使得位错密度降低,在没有发生不连续屈服的情况下,变形就已经结束。周久惠和黄明志[38]通过研究认为,不连续屈服的发生是一种塑性失稳现象,在此塑性变形范围内,材料的应变硬化作用必须小,否则,材料的不连屈服就会被应变硬化作用所掩盖,太高的应变速率不利于不连续屈服的发生。而太低的应变速率又有利于动态再结晶现象在较小的应变下发生,应力在增大的同时由于动态再结晶的软化作用而减小,限制了不连续屈服的发生;
2) 不连续屈服现象随变形温度和应变速率的变化规律较为复杂。JIA等[39]在研究Ti60高温变形时发现屈服下降程度随着变形温度的升高而下降,也不是随着应变速率的升高而一直升高(见图8),有别于1.2节的讨论和图4所示的规律;LI等[40]在研究Ti-3Al-5V-5Mo合金以及ZENG等[41]在研究Ti-B19钛合金时,发现在较高的应变速率下,在β相区和(α+β)相区均出现不连续屈服现象,发生不连续屈服的温度区间较宽;
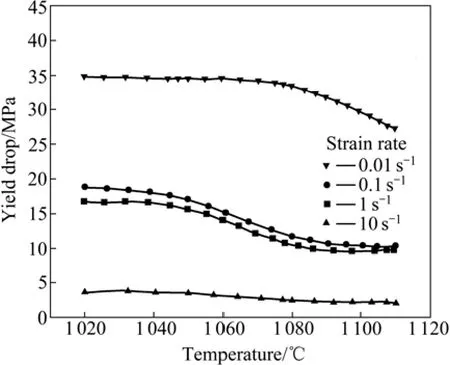
图8 Ti60屈服下降随温度和应变速率的变化[39]Fig.8 Magnitude of yield drop of Ti60 as function of deformation temperature and strain rate[39]
3) 引发变形初期可动位错密度较低的因素较多。LI等[40]认为Ti-3Al-5V-5Mo合金试样在变形初始阶段较低的位错密度是由于退火过程和热压缩变形前试样的加热造成位错的湮灭,以及钛合金机体中固溶的大量Mo元素对于位错的钉扎作用,该影响因素不同于3.1节有关变形前较低可动位错密度的讨论;
4) 两相区变形过程中,发生不连续屈服时,具有影响峰值应力的其它因素。DUAN等[42]认为在(α+β)相变形初始阶段,不连续屈服应力峰的出现与少量 α相的出现有关,因为α相比β相硬,在位错的钉扎上起着重要的作用,能够引发更高的流动应力。
4 发生不连续屈服的钛合金高温变形机制
4.1 下屈服点前的变形机制
由3.1节分析可知,塑性变形初期位错密度处于较低的水平,不连续屈服过程中伴随着大量可动位错的出现,流动曲线上有较为明显的峰值应力,因此初期的塑性变形必定伴随着急剧的应变硬化。
但是对屈服应力急剧下降阶段的变形机制没有统一的认识。目前多数研究者认为该阶段的应力急剧下降是由于β相中的动态回复突然增加。而HAHN[6]、YOSHIDA[9]和WANG等[10]认为,合金在该阶段只发生了应变硬化,急剧的屈服应力下降是可动位错大量增殖和位错速度与宏观剪切应力之间关系共同作用的结果。
本文作者倾向于HAHN[6]、YOSHIDA[9]和WANG等[10]的理论解释,因为虽然动态回复会在一定程度上减少材料中的位错密度,降低宏观流动应力,但是动态回复过程的发生不可能完全消除应变硬化的作用,引发流动应力急剧下降,低于峰值应力,两者最多达到一种动态平衡。WANG等[10]对Ti-20V-4Al-1Sn的高温变形组织观察支持该解释。Ti-20V-4Al-1Sn高温变形时,在发生不连续屈服的变形阶段,晶界处位错密度出现明显增加,晶粒无明显变化;只是当变形至大应变区时,大量堆积的位错才在温度和塑性应变的综合作用下出现晶粒被明显的拉长,呈现动态回复特征。特别是在应变速率为0.1 s−1变形条件下,直至应变为0.4时,才发现晶粒被明显拉长,晶粒晶界处出现凹凸,呈现动态回复特征[43]。
4.2 下屈服点后的变形机制
由1.2节可知:下屈服点后的流动曲线主要呈现无应变硬化阶段和有轻微应变硬化阶段,随后呈现动态平衡和持续软化的特征。针对这些曲线特征所反映的变形机制,部分研究者根据合金的变形情况和微观组织观察,进行了相应的讨论。
1) 广泛认识到钛合金高温变形发生不连续屈服时,下屈服点过后稳态流动的曲线特征是动态回复软化作用与应变硬化作用达到动态平衡的结果[17]。
2) ZENG等[41]将下屈服点过后的持续软化现象归结于钛合金高温变形过程中出现的温升效应,而王震等[1]认为钛合金(α+β)相变形及高应变速率屈服后的软化主要是由于α相中动态微观组织的变化;WANJARA等[18]将在β相出现的持续软化现象归结于动态回复和动态再结晶的共同作用;WANG等[10]则认为这种单相区的持续软化是统计上的可动位错密度继续增加,位错移动速度持续下降和动态回复共同作用的结果。
目前,针对钛合金发生不连续屈服的高温变形机制,虽有研究者对其进行了一定的研究,但由于钛合金变形机制比较复杂,上述研究仍远远达不到研究钛合金高温变形的需要。同时即使是针对相同的材料、相同的变形特性,不同的研究者对其变形机制也有不同的解释。因此需要研究者基于微观组织观察进行更为深入的研究。
5 描述发生不连续屈服的钛合金高温变形本构模型
对于钛合金高温变形的不连续屈服现象,虽然大部分研究者倾向于采用动态增殖理论进行解释,但是至今只有 WANG等[32]基于吉田综仁提出的 Yoshida模型[44],遵从 3.1.2节的位错增殖理论,根据统一粘塑性理论,建立了描述Ti-20V-4Al-1Sn钛合金在高温下出现不连续屈服的本构模型,并用该模型进行了单轴拉伸和V型弯曲过程的有限元模拟计算。具体本构模型如下所示[32]:式中:▽
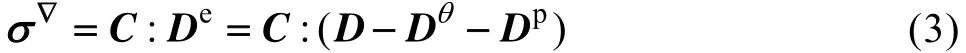
σ 为Jaumann客观应力率张量,C为四阶各向同性弹性张量,D为变形速率,De为弹性变形速率,
D
θ为热应变变形速率,Dp为粘塑性变形速率。

式中:σ为等效应力,s为应力偏量张量。

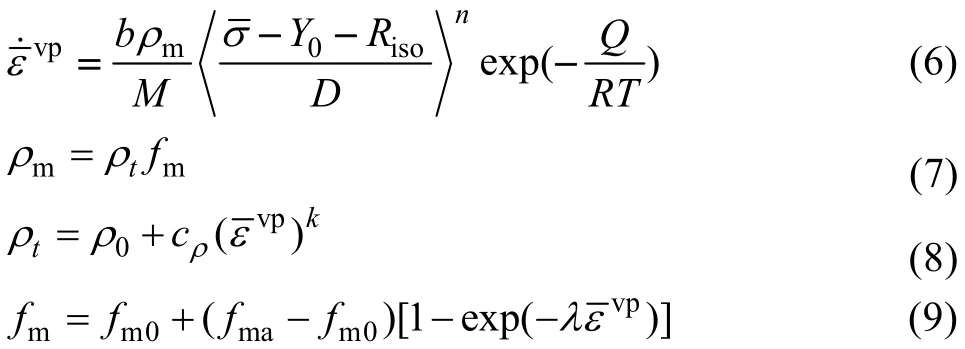
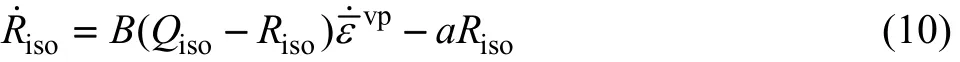
该本构模型较好地描述了钛合金高温变形出现的不连续屈服、急剧的应力下降、下屈服点后的应变软化(图 9所示),具有较好的外推能力。但是把初始屈服应力等在高温变形过程中明显随着变形温度和应变速率变化而变化的参量当成常量来处理,不能很好地反映合金真实的变形特性。
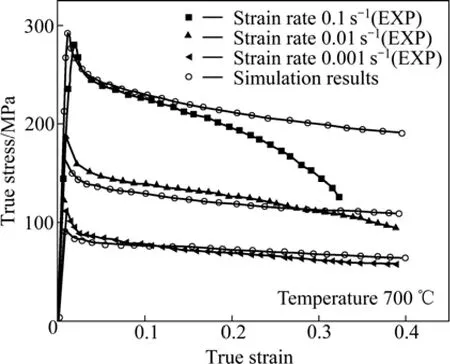
图9 Ti-20V-4Al-1Sn计算结果和实验流动曲线的对比[32]Fig.9 Comparison of simulation results and experiment flow curves[32]
6 当前描述钛合金高温变形不连续屈服存在的不足
钛合金高温变形以及不连续屈服的发生是包含复杂变形机理的过程,虽然目前对其有了一定的研究,对一些现象进行了解释,但仍存在许多不足,需要今后进一步研究、解决。
6.1 描述不连续屈服的基本理论存在的不足
1) 虽然很多研究者关注到了钛合金高温变形的不连续屈服现象,但是从具体理论上还不能对这种现象进行充分有效的物理解释。钛合金高温变形发生不连续屈服时,许多微观组织变化情况不易观察,缺乏对理论解释的实验支撑。
2) 对于钛合金高温变形屈服点附近出现的应力上下剧烈波动现象还缺乏有效的理论解释(见图10)。
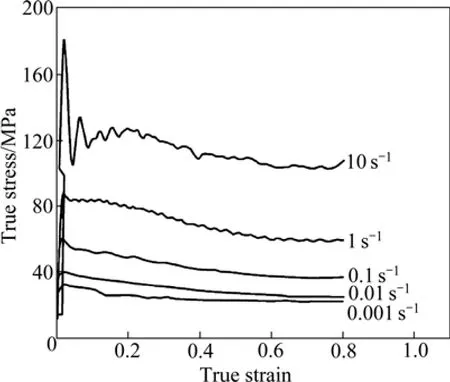
图10 Ti-Al-Zr-Sn-Mo-Si-Y钛合金在1 050 ℃温度下的流动曲线[45]Fig.10 Flow curves of Ti-Al-Zr-Sn-Mo-Si-Y titanium alloy at 1 050 ℃[45]
3) 对于钛合金高温变形,下屈服点过后流动曲线上出现的轻微硬化现象(见图6),目前还没有相关的物理解释。对于下屈服点过后,通过微观组织观察,存在动态再结晶机制的流动曲线特性,目前还缺乏较为理想的物理解释。
6.2 描述发生不连续屈服的钛合金高温变形本构模型存在的不足
1) 当前描述发生不连续屈服的钛合金高温变形本构模型,参数量太多,计算复杂,工程应用受到严重阻碍;
2) 虽然 WANG[32]等有效构建了描述发生不连续屈服的钛合金高温变形本构模型,但是仍缺乏有效描述1.2节流动曲线具有2)、3)和4)特性的成熟本构模型;
3) 如1.1节所述,钛合金高温变形发生不连续屈服时,不出现吕德应变或屈服平台,缺乏有效将屈服下降过程与后续变形过程较好区分开的方法,不利于相应的塑性应变的确定,影响本构模型的构建。
7 结论
1)对于发生不连续屈服的钛合金高温变形流动曲线特性、影响不连续屈服的因素、构建本构模型方法以及当前研究中存在的不足等进行的有效归纳和分析,有利于对发生不连续屈服的钛合金高温变形的理解和构建真实反映钛合金高温变形的本构模型,为数值模拟计算提供较好的前提。
2) 钛合金的高温变形特性对其在航空航天领域的使用上起着重要的作用。不连续屈服现象作为该材料高温变形时流动曲线上的一种重要而又广泛存在的特征,几年来,虽然部分学者对其进行了一定的研究,但是由于钛合金高温变形特性的复杂性,不连续屈服机理的复杂性,当前研究对于发生不连续屈服的钛合金变形机理的解释仍十分有限,需要对其进行更深入的研究,以解决当前研究中存在的不足,满足实际应用的需求。
3) 本构关系能够反映材料的变形特性,在热成形模拟中起着重要的作用,而且准确可靠的本构模型是进行有限元计算的前提保证。但是当前能够描述发生不连续屈服的钛合金高温变形本构模型还十分匮乏,制约了近α、β钛合金的高温热模拟计算。
REFERENCES
[1] 王 震, 洪 权, 赵永庆. 钛合金热变形行为研究[J]. 钛工业进展, 2010, 27(3): 1033−1043.WANG Zhen, HONG Quan, ZHAO Yong-qing. Hot deformation behavior of titanium alloy [J]. Titanium Industry Processing, 2010, 27(3): 1033−1043.
[2] WEISS I, SEMIATIN S L. Thermomechanical processing of beta titanium alloys-an overview [J]. Materials Science and Engineering A, 1998, 243: 46−65.
[3] ZENG Li-ying, GE Peng, MAO Xiao-nan, ZHAO Yong-qing,ZHOU Lian. Hot compression behavior of one kind of metastable β titanium alloy [J]. International Journal of Modern Physics B, 2009, 23(6/7): 777−782.
[4] WARCHOMICKA F, STOCKINGER M, DEGISCHER H P.Quantitative analysis of the microstructure of near β titanium alloy during compression tests [J]. Journal of Materials Processing Technology, 2006, 177: 473−477.
[5] ZEROVNIK A, KUNC R, PREBIL I. Yield-point phenomena in constitutive models of cyclic plasticity [J]. Computational Materials Science, 2010, 49: 473−482.
[6] HAHN G T. A model for yielding with special reference to the yield-point phenomena of Iron and related bcc metals [J]. Acta Metallugica, 1962, 10: 727−738.
[7] SHIOYA T, SHIOIRI J. Elastic–plastic analysis of the yield process in mild steel [J]. Journal of the Mechanics and Physics of Solids, 1976, 24: 187−204.
[8] ITOH M, YOSHIDA F, YAMASHITA F, OHMORI Y M. FEM analysis for nonuniform yielding processes in mild steel plates under stretching [J]. JSME International Journal, 1992, 35(1):70−77.
[9] YOSHIDA F. A constitutive model of cyclic plasticity [J].International Journal of Plasticity, 2000, 16: 359−380.
[10] WANG X, HAMASAKI H, YAMAMURA M, YAMAUCHI R,MAEDA T, SHIRAI Y, YOSHHIDA F. A study of high temperature viscoplastic deformation of beta titanium alloy considering yield-point phenomena [J]. Key Engineering Materials, 2009, 410/411: 177−185.
[11] VASSEL A. Microstructural instabilities in beta titanium alloys[C]// EYLON D, BOYER R R, KOSS D A. Beta Titanium Alloys in the 1990s. Warrendale: TMS, 1993: 173−185.
[12] 赖运金, 曾卫东, 张 弛, 周建华, 王晓英, 俞汉清, 周义刚.Ti-17合金高温变形中的不连续屈服与流变软化研究[J]. 机械科学与技术, 2007, 26(9): 1183−1186.LAI Yun-jin, ZENG Wei-dong, ZHANG Chi, ZHOU Jian-hua,WANG Xiao-ying, YU Han-qing, ZHOU Yi-gang. Study of discontinuous yielding and flow softening in high temperature deformation of Ti-17 alloy [J]. Mechanical Science and Technology for Aerospace Engineering, 2007, 26(9): 1183−1186.
[13] PHILIPPART I, RACK H J. high temperature, high strain deformation behavior of Ti-6.8Mo-4.5Fe-1.5Al [J]. Materials Science and Engineering A, 1998, 254: 253−267.
[14] WANG X, HAMASAKI H, YAMAMURA M, YAMAUCHI R,MAEDA T, SHIRAI Y, YOSHIDA F. Yield-point phenomena of Ti-20V-4Al-1Sn at 1 073 K and its constitutive modelling [J].Materials Transactions, 2009, 50: 1576−1578.
[15] LONG M, RACK H J. High temperature discontinuous yielding in β phase Ti3Al(Nb, Mo) alloys [C]// BLENKINSOP P A,EVANS W J, FLOWER H M. Titanium 1995, Science and Technology. London: The Institute of Materials, 1996: 316−323.
[16] BALASUBRAHMANYAM V V, PRASAD Y V R K.Deformation behaviour of beta titanium alloy Ti-10V-4.5Fe-1.5Al in hot upset forging [J]. Materials Science and Engineering A, 2002, 336: 150−158.
[17] VUAYSHANKAR M N, ANKEM S. High temperature tensile deformation behavior of β-Ti alloys [J]. Materials Science and Engineering A, 1990, 129: 229−237.
[18] WANJARA P, JAHAZI M, MONAJATI H, YUEB S,IMMARIGEON J P. Hot working behavior of near-α alloy IMI834 [M]. Materials Science and Engineering A, 2005, 396:50−60.
[19] WANG Rui-ning, XI Zheng-ping, ZHAO Yong-qing. Hot deformation microstructure and mechanism of Ti5331S titanium alloy [J]. Rare metal Material and Engineering, 2008, 37(8):1356−1359.
[20] COTTRELL A H, BILBY B A. Dislocation theory of yielding and strain ageing of Iron [J]. Proceedings of the Physical Society A, 1949, 62: 49−62.
[21] JONAS J J, HERITIER B, LUTON M J. Anneal hardening and flow softening in beta zirconium-niobium alloys [J].Metallurgical Transactions A, 1979, 10: 611−620.
[22] ANKEM S, SHYUE J G, VIGAYSHANKAR M N. The effect of volume percent of phases on the high temperature tensile deformation of two-phase TiMn alloys [J]. Materials Science and Engineering A, 1989, 111: 51−61.
[23] SRINIVASAN R, WEISS I. High temperature deformation of near β Ti-15V-3Cr-3Sn-3Al alloy [C]// EYLON D, BOYER R R,KOSS D A. Beta Titanium Alloys in the 1990s. Warrendale: The Minerals Metals & Material Society, 1993: 283−295.
[24] JOHNSTON W G, GILMAN J J. Dislocation Velocities,dislocation densities, and plastic flow in lithium fluoride crystals[J]. Journal of Applied Physics, 1959, 30: 129−143.
[25] 陈进化. 位错基础 [M]. 上海: 上海科学技术出版社, 1983:195.CHEN Jin-hua. Dislocation basic [M]. Shanghai: Shanghai Technology Press, 1983: 195
[26] 徐 斌, 曾卫东. 何德华, 周义刚, 梁晓波, 李世琼. Ti-22Al-25Nb 合金热变形行为研究[J]. 铸造锻压, 2007, 36(1): 1−4.XU Bin, ZENG Wei-dong, HE De-hua, ZHOU Yi-gang, LIANG Xiao-bo, LI Shi-qiong. Study on hot deformation behavior of Ti-22Al-25Nb alloy [J]. Casting & Forming, 2007, 36(1): 1−4.
[27] HAN B, XU Z. Microstructural evolution of Fe-32%Ni alloy during large strain multi axial forging [J]. Materials Science and Engineering A, 2007, 447(1/2): 119−124.
[28] FRATIINI L, BUFFA G. CDRX modeling in friction stir welding of aluminum [J]. International Journal of Machine Tools and Manufacture, 2005, 45(10): 1188−1194.
[29] MCQUEEN H J. Development of dynamic recrystallization theory [J]. Materials Science and Engineering A, 2004, 387/389:203−208.
[30] BUSSO E P. A continuum theory for dynamic recrystallization with microstructure-related length scales [J]. International Journal of Plasticity, 1998, 14: 319−353.
[31] ROBERTSON D G, MCSHANE H B. Isothermal hotdeformation behaviour of metastable β titanium alloy Ti-10V-2Fe-3Al [J].Materials Science and Technology, 1997, 13: 575−583.
[32] WANG Xiao-teng, YAMAUCHI R, HAMASAKI H, YOSHID A F, NAGASHIMA K, MAEDA T. High temperature yield drop of β titanium alloy Ti-20V-4Al-1Sn and its modeling [J]. Current Advance in Materials Processing, 2008, 21: 703−706.
[33] SRINIVASAN R. Yield points during the high temperature deformation of Ti-15V-3Ai-3Cr-3Sn alloy [J]. Scripta Metalurgica et Materiallia, 1992, 27: 925−930.
[34] 俞汉清, 陈金德. 金属塑性成形原理[M]. 北京: 机械工业出版社, 1999: 24.YU Han-qing, CHEN Jin-de. Engineering plasticity theory and application to metal forming processes [M]. Beijing: China Machine Press, 1999: 24.
[35] WANG Rui-ning, XI Zheng-ping, ZHAO Yong-qing. Hot deformation behavior and microstructural variation of Ti53311S alloy [C]// The Proceedings of the China Association for Science and Technology. Beijing: CAST, 2007: 85−88.
[36] 张树志. Ti-46Al-2Cr-4Nb-0.3Y 合金高温流变行为及加工图研究 [D]. 哈尔滨: 哈尔滨工业大学, 2009.ZHANG Shu-zhi. Study on hot deformation behavior and processing map of Ti-46Al-2Cr-4Nb-0.3Y alloy [D]. Harbin:Harbin Institute of Technology, 2009.
[37] BALASUBRAHMANYAM V V, PRASAD Y V R K. Hot deformation mechanisms in metastable beta titanium alloy Ti-10V-2Fe-3Al [J]. Material Science and Technology A, 2001,17: 1222−1228.
[38] 周久惠, 黄明志. 金属强度学[M]. 北京: 科学技术出版社,1989: 128.ZHOU Jiu-hui, HUANG Ming-zhi. Strength of metal [M].Beijing: Science and Press, 1989: 128.
[39] JIA Wei-ju, ZENG Wei-dong, ZHOU Yi-gang, LIU Jian-rong,WANG Qing-jiang. High temperature deformation behavior of Ti60 titanium alloy [J]. Materials Science and Engineering A,2011, 528: 4068−4074.
[40] LI L X, LOU Y, YANG L B, PENG D S, RAO K P. Flow stress behavior and deformation characteristics of Ti-3Al-5V-5Mo compressed at elevated temperatures [J]. Materials and Design,2002, 23: 451−457.
[41] ZENG Li-ying, YANG Guan-jun, GE Peng, MAO Xiao-nan,ZHAO Yong-qing, ZHOU Lian. Processing map of one kind of metastable β titanium alloy [J]. Rare Metal Materials and Engineering, 2010, 39(9): 1505−1508.
[42] DUAN Yuan-pei, LI Ping, XUE Ke-min, ZHANG Qing, WANG Xiao-xi. Flow behavior and microstructure evolution of TB8 alloy during hot deformation process [J]. Transactions of Nonferrous Metals Society of China, 2007, 17: 1199−1204.
[43] WANG Xiao-teng, FANG Hong-yuan, YOSHIDA F. In situ AFM observation of mechanical behavior of beta titanium alloy in nano-indentation test [J]. Materials Science Forum, 2007,546/549: 1356−1359.
[44] YOSHIDA F, KANEDA Y, YAMAMOTO S. A plasticity model describing yield-point phenomena of steels and its application to FE simulation of temper rolling [J]. International Journal of Plasticity, 2008, 24: 1792−1818.
[45] QI Yun-lian, XI Zheng-ping, ZHAO Yong-qing, WANG Rui-ning, DU Yu, LUO Yuan-yuan, ZENG Wei-dong. Hot deformation behavior and microstructure evolution of titanium alloy Ti-Al-Zr-Sn-Mo-Si-Y [J]. Transactions of Nonferrous Metals Society of China, 2007, 17: 537−540.
(编辑 何学锋)
Research and development progress of high temperature deformation of titanium alloy with discontinuous yielding
WANG Zhe-jun, QIANG Hong-fu, WANG Xue-ren
(601 Staff Room, Xi’an Hi-Tech Institute, Xi’an 710025, China)
TG146.2
A
1004-0609(2012)07-1904-10
2011-06-09;
2011-12-12
强洪夫,教授,博士;电话:029-84743418;E-mail: qiulongzaitian@126.com流动曲线特性还没有得到较好的物理解释,能完整描述发生连续屈服的钛合金高温变形本构模型仍十分匮乏,需要开展大量的工作。因此,深入系统地开展发生不连续屈服的钛合金高温变形研究和相应的本构模型研究,对钛合金的工程应用有重要的指导意义。

