市场细分下定价与交货延迟批量的联合决策

戴道明

（安徽财经大学 管理科学与工程学院，安徽 蚌埠 233030）

由于互联网的迅猛发展，以及直接面向顾客（Direct－to－Customer，简称 DTC）订货方式的广泛采用，制造商可以从互联网上获得大量有关顾客偏好和需求方面的信息，且价格变动所产生的费用非常低。因此，动态定价策略在零售业和制造业中掀起了一场重要的变革。

大多数定价与生产／库存的联合决策问题致力于单周期情形［1－3］。在这些模型中，价格是决策变量，需求是关于价格的单调减函数。研究的焦点在于设计算法（如微分法、求导或迭代法等），以便求得最优价格和最优订货量。

也有不少文献研究多周期定价与生产／库存的联合决策问题。文献［4］提出了逐期评审（s，S，p）策略；文献［5］探讨了政府和 WEEE回收法规对两周期新制造产品与再制造产品差异定价策略和利润的影响；文献［6］研究了新制造产品和再制造产品差异销售情形，结果表明2种产品的数量在相邻周期间交替占优。

在以上提及的文献中，周期的跨度预先未知，在企业生产管理实际应用中带来诸多不便。基于MRP的定价与生产／库存的联合决策问题［7－10］，预先把计划期划分成若干个周期（周期为月、旬或自然周等），在实际生产管理活动中易于操作。其模型和方法可以作为常用管理软件（如MRPII、ERP等）的模型库和方法库。这类联合决策问题一般运用组合技术进行求解，涉及价格和生产量2类决策变量，求解方法比较复杂。

文献［7］研究了考虑价格折扣的订货批量问题；文献［8］研究了订货费用和库存费用是动态情形的定价和批量的联合决策问题；文献［9］研究生产能力受限情形下制造／再制造混合批量问题，设计了一种启发式蚁群优化算法；文献［10］研究了随机提前期的批量问题，提出了动态规划算法。

面对激烈的市场竞争，企业常常按照一定的标准将市场划分成若干个子市场，针对每个子市场的特点分别采取不同的定价策略和生产策略，以便获得最佳效益。本文针对市场细分情形，研究基于MRP的动态定价与允许交货延迟批量的联合决策问题，提出基于动态规划的精确算法。

1 数学模型

设T为计划期内的周期数；Mt为第t周期的子市场数；Kt为第t周期的生产启动费用；vt为第t周期的单位产品变动生产费用；为第t周期的单位产品存贮费用为第t周期的单位产品延迟费用；γ为允许交货延迟的最大周期数；dmt为第t周期第m 子市场的需求量；pmt（dmt）＝αmt－βmtdmt，为第t周期第m 子市场的价格函数；dt为第t周期的所有子市场的需求之和；xt为第t周期的生产量；为第t周期末的库存量；为第t周期的交货延迟量；第t周期如果生产则yt取1，否则取0。问题的数学模型如下：

模型Ⅰ：

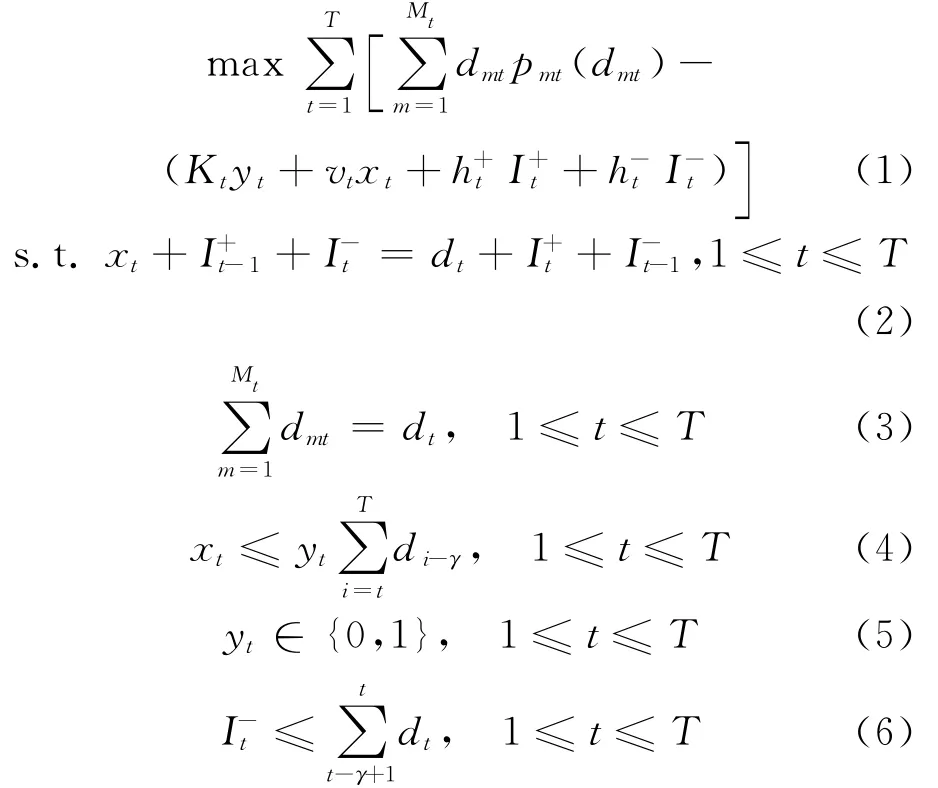
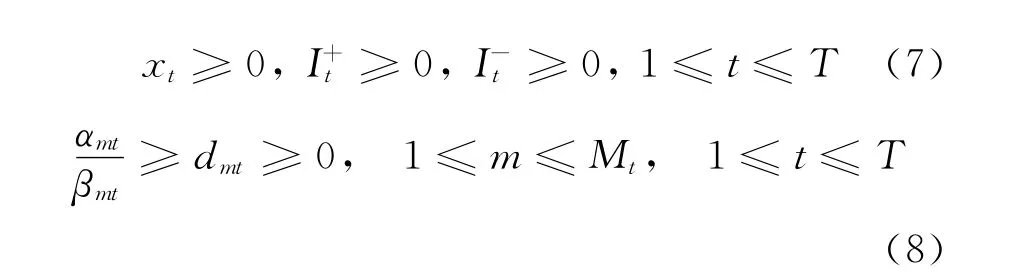
目标函数（1）是制造商的利润；约束条件（2）是相邻周期间的物料平衡方程；约束条件（3）要求每个周期所有子市场的需求量之和等于该周期的总需求量；约束条件（4）规定了生产量的上限；约束条件（5）表示某周期是否生产；约束条件（6）要求未被满足的交货延迟的期限不能超过γ个周期；约束条件（7）要求相关变量的非负性；约束条件（8）要求每个周期各个子市场的需求量和价格是非负的。目标函数（1）中是第t周期的收益。当第t周期的各子市场需求量之和为dt时，考虑下面的模型。

模型Ⅱ：

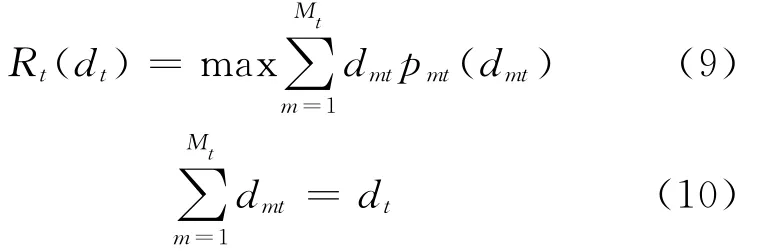
令Rmt（dmt）表示第t周期第m 子市场的收益，即Rmt（dmt）＝dmtpmt（dmt）。由pmt（dmt）定义可知，Rmt（dmt）处处可微，且是凹函数。模型Ⅱ的库恩－塔克条件为：

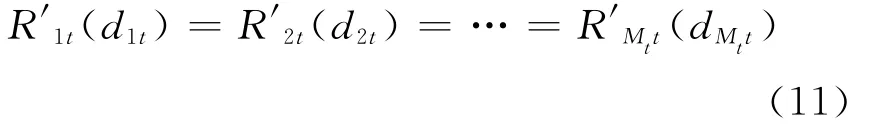
通过（10）式和（11）式可以分别求解出d1t，…，dMtt关于dt的函数表达式，令

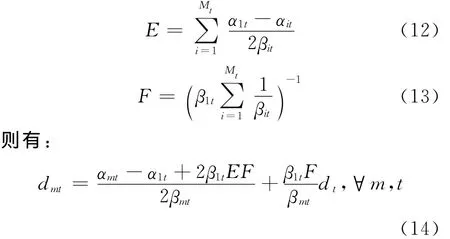
令Rt（dt）表示周期t的需求量为dt时，周期t的最大收益。由于d1t，d2t，…，dMtt仅仅通过dt与批量决策相关联，因此模型Ⅱ和下面的模型Ⅲ联合起来等价于模型Ⅰ。

模型Ⅲ：

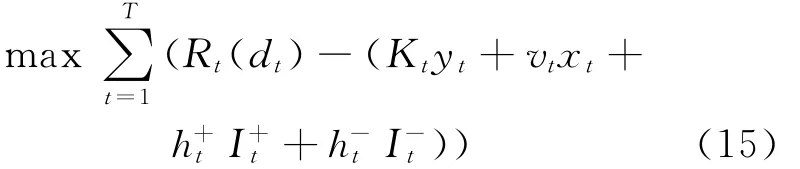
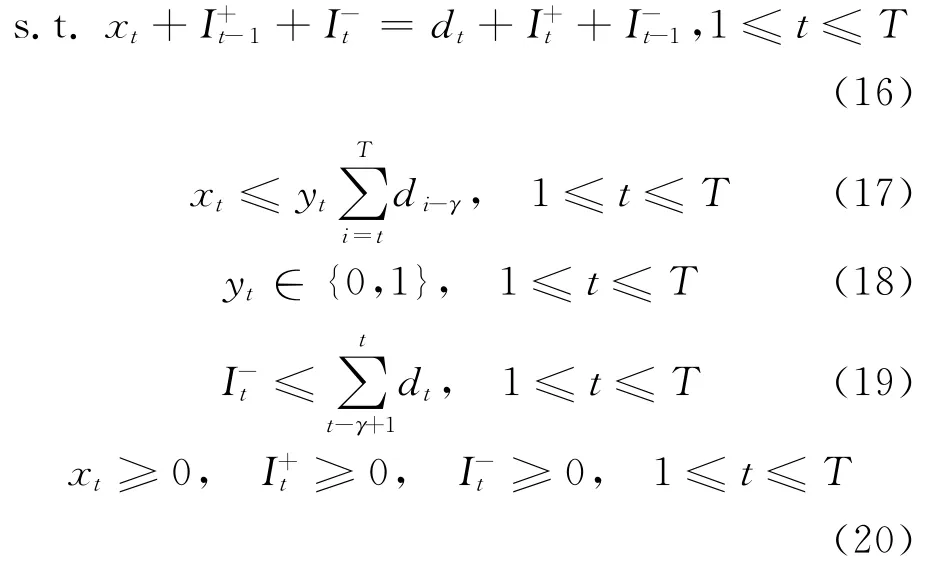
2 最优解性质分析

令D＝｛d1，…，dT｝表示从周期1到周期T的需求向量，X（D）表示需求向量为D时的可行生产计划。

定义2 如果Sab（1≤a＜b≤T）表示生产计划X（D）的一个子集，且Sab＝｛xi，a≤i＜b｜a－1和b是再生点＞0或＞0，a≤j＜b｝，则称Sab是生产计划X（D）的子生产计划，相应的问题称为子问题（a，b）。特别地，如果a－1和a都是再生点，则Saa也是生产计划X（D）的子生产计划。

定理1 给定需求向量D＝｛d1，…，dT｝，存在某个最优生产计划，具有以下性质：在任意2个连续的生产点t0、t1（1≤t0＜t1≤T）间，至少存在1个再生点j，t0≤j＜t1；也就是说，在任意2个连续的再生点间，至多存在1个生产点。

证明 反证法。假设最优生产计划X（D）存在连续生产点t0、t1，它们之间没有再生点，即＞0或＞0（t0≤i＜t1）。分3类：①＞0（t0≤i＜t1）；②＞0（t0≤i＜t1）；③ 存在某个周期j0（t0＜j0＜t1）＞0且＞0。以第3类为例进行证明，分2种情形讨论。

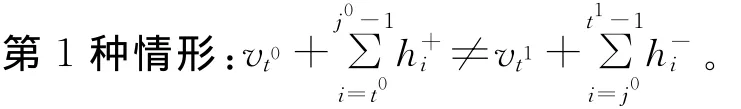
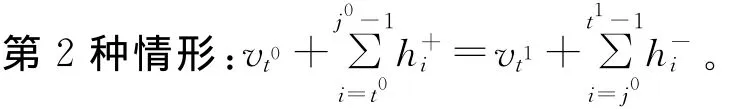
这时，周期j0的需求既可以全部由生产点t0来满足（此时，Ij0＝0），也可以全部由生产点t1来满足（此时，Ij0－1＝0），总费用不变。因此，存在某个最优解X′（D），具有定理1的性质。

第1类取j0＝t1－1；第2类取j0＝t0，可以类似地证明。证毕。

由定理1可知，存在某个最优生产计划，任意2个连续的再生点，至多有1个生产点。因此，很容易得到下面的推论。

推论1 存在某个最优生产计划，对于任意周期t，要么不生产，要么生产量是几个连续周期的需求量之和。

设周期t0是生产点，令周期r（t0）表示不超过周期t0的最迟的再生点。

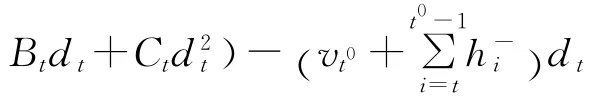
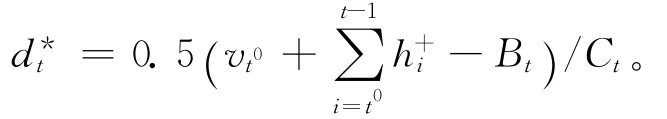
证明 存在最优解X（D＊＊），其中D＊＊＝，…，｝。t0和t1（t0＜t1）是 X（D＊＊）的任意2个连续的生产点。由于从周期r（t0）＋1到r（t1）只有1个生产点t0，故对于周期t，其中r（t0）＋1≤t≤（t0－1），需求量分别为和时，利润之差为：

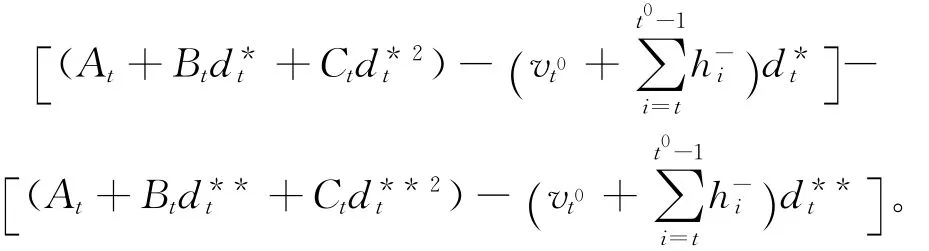
综上所述，需求向量D＊＝，…，｝也是原问题的一个最优需求向量。证毕。

3 算法及计算复杂度

3.1 模型Ⅱ的求解方法

Rt（dt）是关于dt的二次函数。不妨设Rt（dt）＝At＋Btdt＋。把（14）式代入到模型Ⅱ目标函数（9）式中，得到：

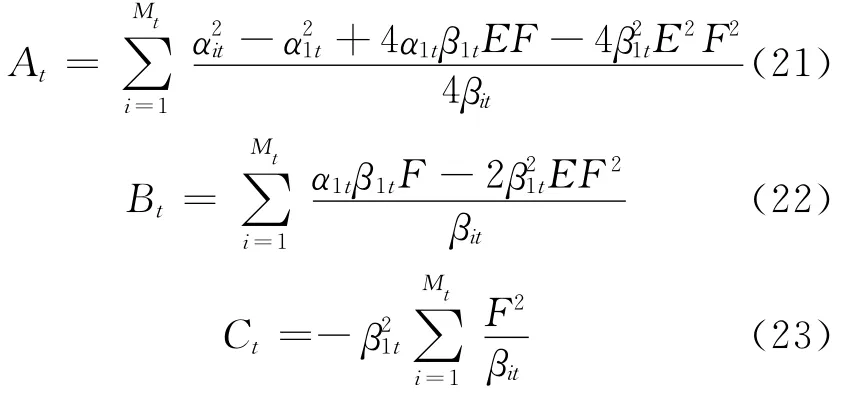
3.2 模型Ⅲ的子问题求解方法

根据定理1，可以把模型Ⅲ分解成若干子问题，分别对子问题进行求解。不失一般性，以子问题（1，n）（1≤n≤T）为例。根据定理1及推论1可知，子问题（1，n）只有1个生产点t（1≤t≤γ＋1）且生产量为子问题所有周期的需求总和。对于给定的生产点，运用定理2可以求解子问题的每个周期的价格。遍历所有可能的生产点，利润最大者所对应的生产计划和需求向量为子问题的最优生产计划和最优需求向量。

令Φ是所有可行D 的集合。E（1，n，t0）表示子问题（1，n）生产点为t0时的最大利润，即

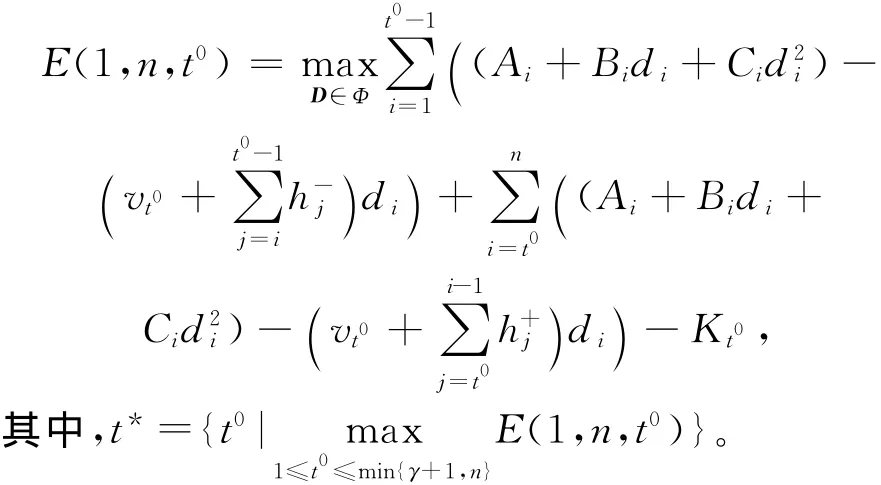
子问题（1，n）的最优需求策略：

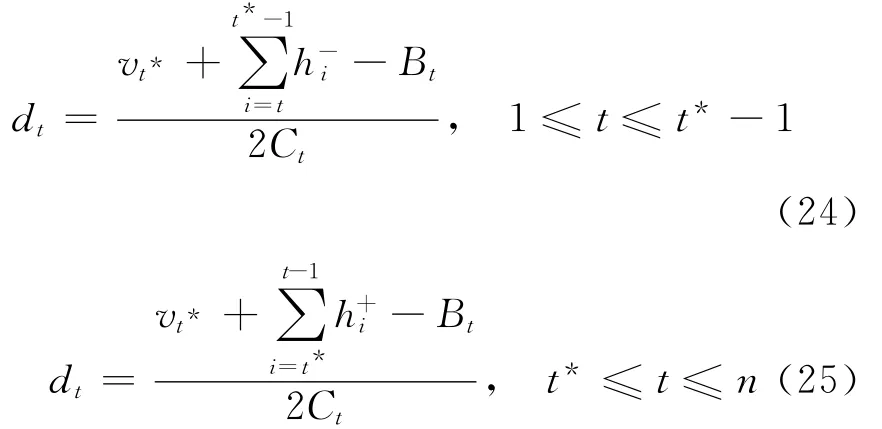
把（24）式和（25）式分别代入（14）式，得到周期t时各子市场的需求量dmt。如果dmt＜0，则令dmt＝0，（12）式和（13）式中不考虑市场m，重新计算需求量为非负的子市场的需求量。直至各子市场需求量非负为止。

子问题（1，n）的最优生产策略：

3.3 模型Ⅲ的求解方法

用动态规划法求解模型Ⅲ。F（k）表示从计划期初到周期k末的总利润。令δ＝min｛i＋γ，k｝。

由定理1，得到动态规划顺序递推公式：

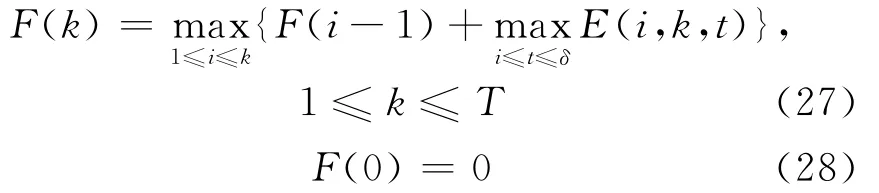
其中，（28）式为初始条件，E（i，k，t）可以根据3.2节中的算法进行求解。F（T）就是模型Ⅲ的最大利润，对应的需求向量（或生产计划）就是模型Ⅲ的最优需求向量（或最优生产计划）。

3.4 计算复杂度分析

模型Ⅱ的时间复杂度为O（T）。对于模型Ⅲ，子问题的时间复杂度为O（T）。模型Ⅲ包含的子问题数是0.5T（T－1），因此，模型Ⅲ的时间复杂度为O（T3）。综上所述，模型Ⅰ的时间复杂度为O（T3）。

3.5 算法的具体步骤

算法的主要步骤如下：

（1）给定周期t，根据（14）式，求得周期t各子市场的需求函数表达式；利用（21）～（23）式求得收益Rt（dt）的函数表达式。

（2）按照步骤（1），求得所有周期收益函数表达式和各子市场的需求函数表达式。

（3）对于i，k，1≤i≤k≤T，运用3.2中的方法求解子问题（i，k）的最优需求量和生产计划。

（4）按照步骤（3），求解所有可能的子问题（i，k）的最优需求向量和最优生产计划。

（5）运用（27）式和（28）式，用动态规划顺推解法求解出模型Ⅲ的最大利润、最优价格向量和最优生产计划。

（6）对于步骤（5）中求得的各周期最优需求量，利用步骤（1）得到的每周期各子市场的需求函数表达式，求得每周期各子市场的最优需求量。

4 实验结果与参数分析

交货延迟的最大周期数γ＝3，每周期的子市场数Mt＝3。根据αjt和βjt的取值特征，把问题分为4种类型。类型Ⅰ：所有子市场的价格函数相同，αjt（j＝1，2，3）的值都等于表1中的α3t，βjt（j＝1，2，3）的值都等于表1中的β1t，其余参数值见表1所列。类型Ⅱ：βjt（j＝1，2，3）的值都等于表1中的β1t，其余参数值见表1所列。类型Ⅲ：αjt（j＝1，2，3）的值都等于表1中的α3t，其余参数值见表1所列。周期t（t＝1，…，T）时，如果每个子市场的价格函数相同，则该周期内各子市场的最优需求量和最优价格是相同的，见表2和表3中的Ⅰ行。如果所有子市场价格函数的βjt（j＝1，2，3）取值相同，αjt（j＝1，2，3）减少，那么子市场的需求量随之降低且价格也随之降低，见表2和表3的Ⅱ行。如果所有子市场价格函数中的αjt（j＝1，2，3）取值相同，βjt（j＝1，2，3）增加，那么子市场的需求量反而随之降低且价格保持不变，见表2和表3的Ⅲ行。如果αjt（j＝1，2，3）减少且βjt（j＝1，2，3）增加，那么子市场需求量下降的幅度更大，见表2和表3的Ⅳ行。综上所述，αjt与子市场需求量（或价格）是正相关的，βjt与子市场需求量是负相关的且与价格不相关。

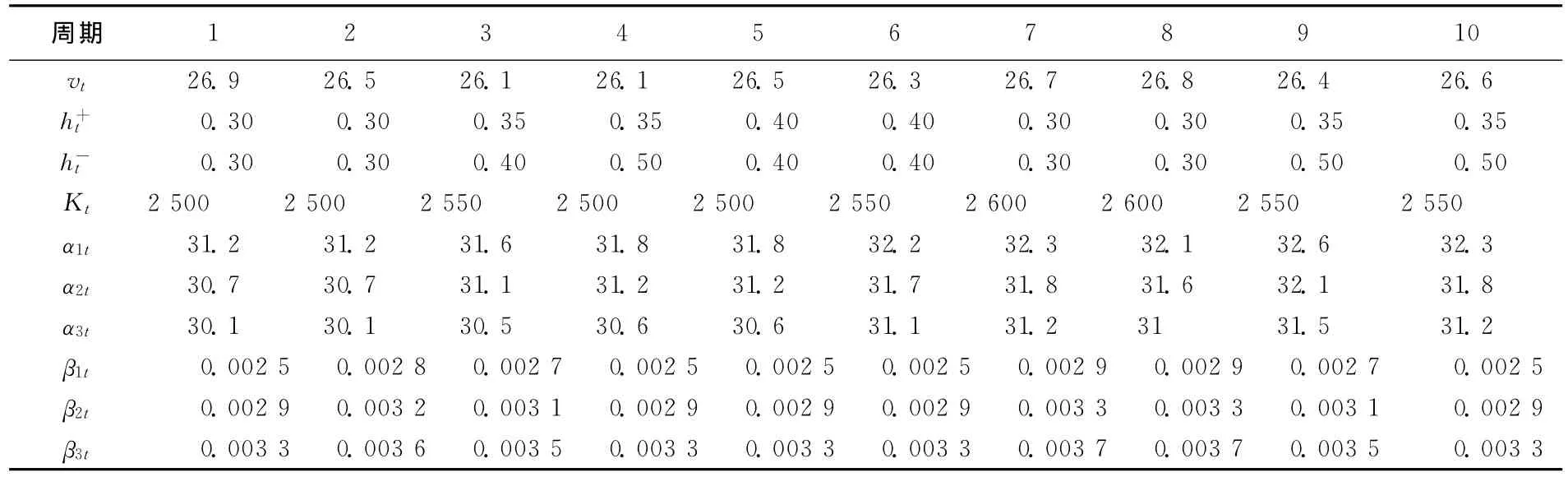
表1 类型Ⅳ的主要参数值

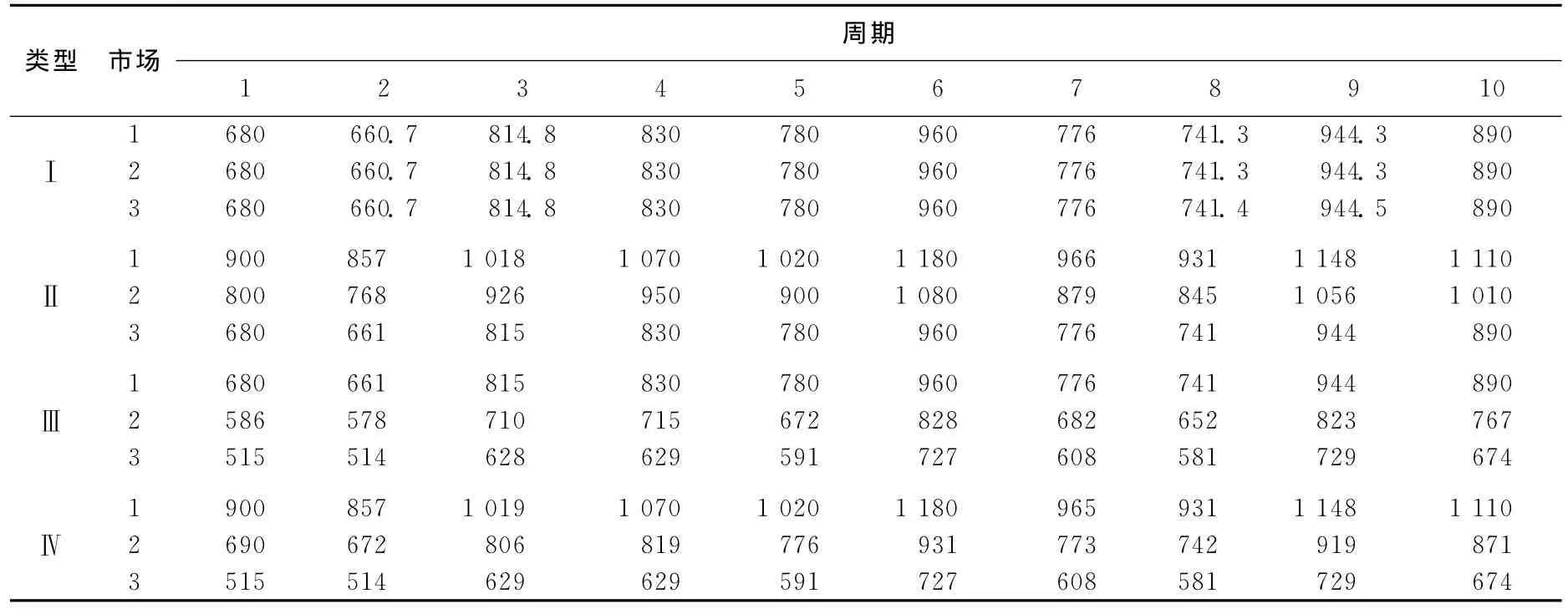
表2 4种类型的各子市场的最优需求 件

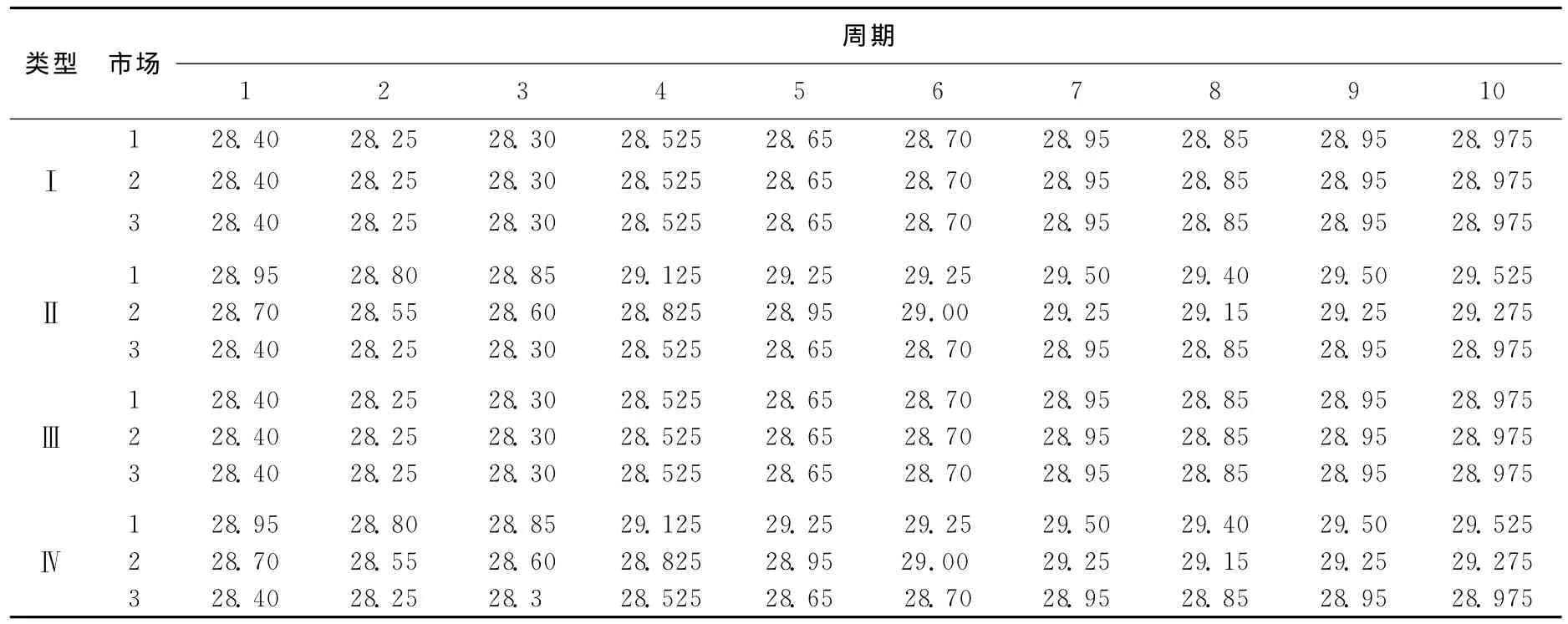
表3 4种类型的各子市场的最优价格 千元

图1分析了不同生产启动费用下，不允许延迟情形下和允许延迟情形下联合决策的利润变化。图1的参数值见表1所列。从图1可以看出，2条曲线呈张开的剪刀形，说明允许交货延迟情形下的联合决策对生产启动费用的变化较为“迟钝”。从管理角度来说，当生产启动费用较大时，采用允许交货延迟的联合决策可以给企业增加更多的利润；当固定费用较小时，2种情形下的利润差别不大。可以从理论角度解释这个现象，当生产启动费用较大时，采用允许交货延迟的联合决策模型可以减少生产启动的次数，如果减少的生产启动费用大于由于生产点的数目减少而增加的延迟费用和库存费用，则利润就会增加。

图1 不许延迟与允许延迟的利润比较

一般来说，联合策略优于分散策略，如图2所示。

图2 分散策略与联合策略的利润比较

图2的参数值见表1所列。分散策略下，选择了13种定价方案。为方便起见，分散策略下的每周期各子问题的价格取值分别是联合决策下最优价格的92%、93%、94%、95%、96%、97%、98%、99%、101%、102%、103%、104%、105%。当倍数大于等于106%时，子市场3周期1的需求量为负，定价方案不可行。从管理角度来看，如果分散策略下价格过低，虽然提高市场占有率，但降低了边际利润率；如果价格过高，虽然提高了边际利润率，但降低了市场占有率。联合决策模型在边际利润率和市场占有率之间找到了平衡点，为每周期各子市场制定了合理的价格水平，使得企业利润最大化。

5 结束语

本文研究了在市场细分情形下，允许交货延迟的批量与定价的协调决策问题，提出了基于动态规划的精确算法，可以在多项式时间O（T3）内求解出每周期各个子市场的最优价格和最优生产计划，获得最大的利润。定价时不仅注重公司的外部因素（通过产品成本、需求函数中的系数αjt和βjt体现），同时也考虑公司的内部因素（生产费用及库存费用等）。模型不仅可以有效解决成熟产品的定价决策与批量决策的协调问题，而且对制造商的新产品定价具有指导意义。

［1］冯 颖，蔡小强，涂奉生，等.随机需求情形下单一易变质产品库存模型的订购与定价策略［J］.南开大学学报：自然科学版，2010，43（2）：106－112.

［2］纪鹏程，宋士吉，吴 澄.动态定价策略下的精确库存成本建模与优化［J］.控制与决策，2010，25（3）：422－425.

［3］Ghosh S K，Khanra S，Chaudhuri K S.Optimal price and lot size determination for a perishable product under conditions of finite production，partial backordering and lost sale［J］.Applied Mathematics and Computation，2011，217：6047－6053.

［4］Chen X，Simchi－Levi D.Coordinating inventory control and pricing strategies：the continuous review model［J］.Operations Research Letters 2006，34：323－332.

［5］Mitra S，Webster S.Competition in remanufacturing and effects of government subsidies［J］.International Journal of Production Ecomomics，2008，111（2）：287－298.

［6］Ferrer G，Swaminathan J M.Manage new and differentiated remanufactured products［J］.European Journal of Operational Research，2010，203（2）：370－379.

［7］Parlar M，Weng Z K.Coordinating pricing and production decisions in the presence of price competition［J］.European Journal of Operational Research，2006，170：211－227.

［8］Heuvel W，Wagelmans A M.A polynomial time algorithm for a deterministic joint pricing and inventory model［J］.European Journal of Operational Research，2006，170：463－480.

［9］马 艳，钟金宏，黄继红，等.允许延期交货的制造／再制造受限批量模型研究［J］.合肥工业大学学报：自然科学版，2010，33（4）：524－528.

［10］Jiang R，Guan Y.An O（N2）－time algorithm for the stochastic uncapacitated lot－sizing problem with random lead times［J］.Operations Research Letters，2011，39：74－77.