计算机辅助三维公差分析技术的研究进展*＊1

彭和平 刘晓军

(①江汉大学机电与建筑工程学院，湖北武汉 430056;②华中科技大学机械科学与工程学院，湖北武汉 430074)

计算机辅助公差(Computer Aided Tolerancing，CAT)是实现CAD、CAPP和CAM集成的核心技术之一。由于计算机辅助公差技术的复杂性，使对公差设计技术特别是三维公差设计技术的研究远远落后于对CAD、CAPP和CAM的研究，使其难以与目前的CAD/CAPP/CAM集成。基于计量学的新一代产品几何技术规范与认证(Geometrical Product Specifications and Verification，简称GPS)标准体系对公差定义的数学化便于计算机识别和公差信息在设计、制造和检验各阶段中的传递，为公差设计理论的研究提供了全新的思路和方法，为计算机辅助三维公差分析与综合技术研究带来了新的契机。同时，新一代GPS标准ISO1101还增加了三维公差标注规范，并且其规范、标准的表示法支持不同三维CAD软件之间的数据交换。早期的公差设计技术主要集中于一维、二维尺寸的公差分析与综合，随着科技的发展，原来进行一维、二维公差分析与综合的尺寸链技术已经不能满足要求，三维CAD软件逐渐成为产品设计的方向和主流。由三维模型直接指导生产时，必须在其上标注公差，如何在三维CAD模型上进行公差分析与综合已成为一个必须解决的问题。国内外学者对三维公差设计技术特别是三维公差分析技术进行了大量研究，取得一定的研究成果。本文对国内外计算机辅助三维公差分析技术的最新研究进展作全面介绍，并对今后的研究工作进行展望。

1 三维公差分析

1.1 TTRS 模型

Desrochers 和 Clément［1］从研究建立独立于 CAD/CAM三维造型系统的公差信息表示模型的角度出发，提出了工艺拓扑关联表面(Technologically and Topologically Related Surface，TTRS)的公差信息表示模型，它是对漂移公差带模型的扩展。TTRS定义为属于同一个实体由于功能原因而关联在一起的一对表面。按照由Clément等提出的7个单元表面类和28个表面相关情形之间的关联类型控制公差。它首先从三维CAD系统中提取必需的信息，将零件的各表面以二叉树的形式组织，形成零件的TTRS二叉树结构，接着构造此TTRS的最小几何基准元(Minimum Geometric Datum Element，MGDE)。根据MGDE及其相互之间的关系，可以确定公差类型，并且公差信息可以添加于MGDE上。该模型最大的特色之处在于提出了TTRS的概念及其组织方式，对三维CAD系统所提供的几何信息进行了重新的组织以便于实现公差信息的添加。但在其具体实现时主要是考虑了拓扑上表面的相联，而对于工艺上表面的关联则未真正考虑。这种公差表示法在欧洲较通用，同时其影响在新的ISO标准中能够体现。

基于TTRS模型进行三维装配公差分析时，首先为装配体创建具有MGDE/MGRS表面识别信息的TTRS图，并创建包含几何公差信息的TTRS图，然后，使用张量、非共面直线对、旋量等参数来表示公差，于是TTRS图直接生成基于张量、非共面直线对、旋量等参数的公差模型;沿着装配中公差累积路径，结合这些参数的限制，识别限定参数的方向，最后将参数求和可以得到目标特征的公差，实现三维装配的公差分析［2］。

1.2 矩阵模型

基于矩阵的公差表示模型使用奇次矩阵变换进行公差建模，它既能描述三维零件之间的名义几何关系，又能描述由其几何偏差引起的变动［3］。例如，如图 1 所示定义在圆柱体内的公差区域的矩阵表示，坐标系(O，x，y，z)建立以线段AB的中点O为坐标原点，y方向沿着圆柱轴线AB方向。于是描述公差带的齐次变换矩阵为［4］。

式中:0≤γ≤π，0≤α≤π

此外，约束条件确保线段AB保持在圆柱公差带边界以内

可见，一个完整公差矩阵模型是由描述轴线AB的偏差矩阵(1)和一组描述公差带几何形状和尺寸的约束方程(2)构成。

绝大多数的公差规范都与矩阵模型兼容，它也能很好地与三维CAD/CAM系统集成。采用矩阵形式建立公差语义，适合于公差信息的计算机表示，为进行三维公差分析提供方便。Desrochers和Rivière在文献［4］中给出了基于矩阵模型的三维公差分析实例。

1.3 矢量环模型

进行三维装配公差分析时，必须充分考虑装配中的3种主要的变动来源:尺寸变动、几何特征变动和装配运动学调整。前面2种变动是由于制造过程中的加工条件及加工工艺的波动、原材料性能差异等因素造成的。第3种变动在产品装配中出现，是由于零件尺寸或形状变化引起的配合零件之间的微小调整。考虑这3种变动的影响，Gao等［5］研究了基于矢量环模型的三维公差分析技术。在该模型中，每个零件尺寸被看作有向矢量，零件尺寸公差表示该矢量的变动;零件的几何公差看作具有一定公差的零长度矢量，加到接触表面的接触处，一起参与公差分析。对于三维装配公差分析所用的矢量环可用一种矩阵环方程描述，矩阵环由一系列变换矩阵乘积确定。

基于矢量环模型的封闭矢量方程式用矩阵形式表示为

式中:A为组成环尺寸偏导数矩阵;B为装配封闭环偏导数矩阵;C为几何特征变量的偏导数矩阵;［ΔX］为组成环尺寸的变动矩阵;［ΔY］为装配封闭环的变动矩阵;［ΔZ］为几何特征变量的变动矩阵。

求解方程(3)，于是装配封闭环的变动矩阵为

式中:sX为尺寸变量的公差灵敏度矩阵;sZ为几何特征变量的公差灵敏度矩阵。

公差灵敏度矩阵一经确定，整个三维装配变动的累积(封闭环公差)可以用WC(Worst Case)模型、RSS(Root Sum Squares)模型或者平均漂移模型确定

WC模型

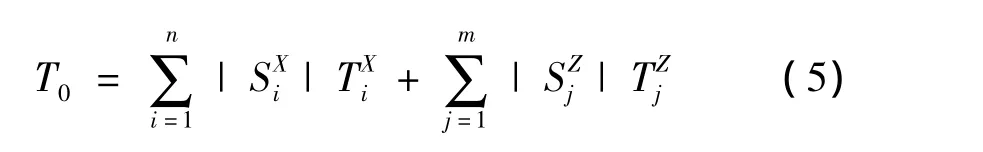
RSS模型

平均漂移模型

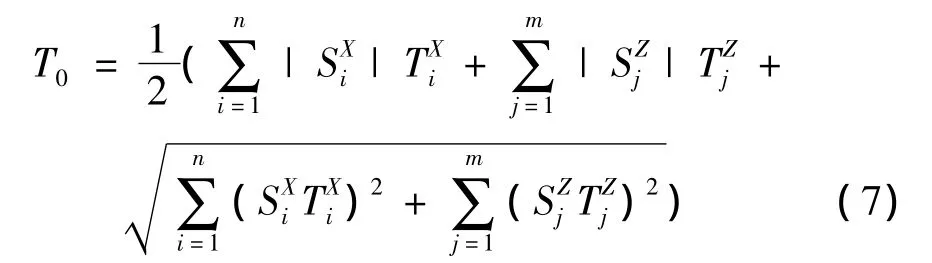
式中:T0表示封闭环公差和分别表示第i个尺寸变量和第j个几何特征变量的公差和分别表示在各个组成环尺寸中尺寸变量和几何特征变量的公差灵敏度;n和m分别表示尺寸变量和几何特征变量的数目。

目前集成于Pro－ENGINEER的三维公差分析软件TI/TOL就是基于该理论。

1.4 基于VDT的三维公差分析

随着工件检验中三维坐标测量机的广泛应用，传统的几何公差定义及原理不能满足离散测量数据的公差评定要求。为了解决这个问题，在20世纪90年代初由Wirtz［6］提出矢量尺寸与公差(Vectorial Dimensioning and Tolerancing，VDT)的概念。1995年，Henzold［7］在其出版的《几何公差的设计、制造及检验手册》中对比进行了发展。相比基于传统的几何尺寸与公差(Geometrical Dimensioning and Tolerancing，GDT)，VDT的替代要素以一种更好的方式规范了工件的几何特征。特别是三维CAD/CAM系统在工程实际中的广泛应用，VDT适合于描述三维模型的名义几何特征以及这些特征的变动，有利于三维公差分析问题的解决。Humienny等［8］提出了基于VDT的计算机辅助三维公差分析的方法。Dantan等［9］还研究了基于VDT的圆锥齿轮的公差设计问题。

1.5 基于GapSpace的三维公差分析

一维 GapSpace 模型较早由 Morse［10］提出，Gap-Space模型中有2个基本概念，其一是有向尺寸树，其二是间隙。有向尺寸树是一种数据结构，用来描述零件一个方向上尺寸的规划，每个有向尺寸树描述唯一的一组特征关系。间隙定义为不同零件的对应特征的相邻规范，即2个特征之间的距离。如图2所示为铰链装配的GapSpace模型，图中有4个间隙g1、g2、g3、g4，它们均为独立变量，构造一个四维线性矢量空间，基底矢量分别为［1 0 0 0］T、［0 1 0 0］T、［0 0 1 0］T、［0 0 0 1］T，这个线性矢量空间即所谓装配的GapSpace。Zou和Morse［11］提出了基于GapSpace模型的统计公差分析方法。Zou［12］在博士论文中，对GapSpace模型进行扩展研究，探讨了GapSpace模型进行二维和三维装配公差分析技术。

1.6 基于T－Map的三维公差分析

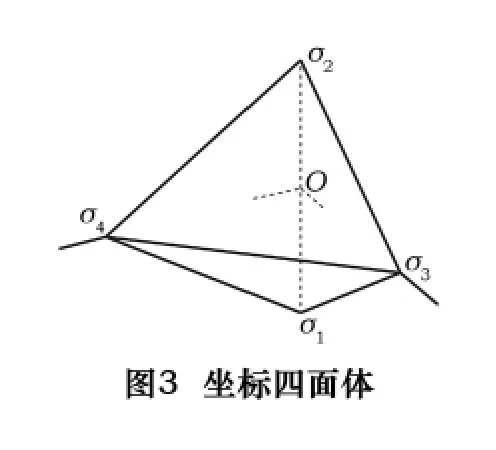
Mujezinovic 等［13］提 出了一个与ASME标准兼容的公差数学模型，其核心是T－Map的概念。T－Map是一个假想的欧氏点空间，其尺寸和形状反映目标特征的所有变动可能性。这些变动由控制特征的尺寸、位置、方向等公差确定。对于特征的三维变动，相应的T－Map由定义基本单形体(四面体)的4个基本点构造而成，并用质心坐标进行描述。如图 3 所示，选择 4 个基本点 σ1、σ2、σ3、σ4，在这4 个点处分别放置 4 个集中质量 λ1、λ2、λ3、λ4，只要λ1+λ2+λ3+λ4≠0，这些质量的质心 σ 的位置将由方程(8)唯一确定。并且可以通过改变 λ1、λ2、λ3和λ4，使质心σ落在四面体空间的任意位置。

如图4所示为矩形平面的T－Map，目前已经开发了圆形平面、多边形平面、圆柱面、圆柱形特征的轴线、槽形等的T－Map图。在用T－Map图进行三维公差分析时，首先生成每个零件的T－Map图;为了描述每个特征的变动，再生成所谓的相似T－Maps;在所有相似T－Maps获得后，需要生成一个累积T－Map图，用于描述装配体中所有零件的变动累积。把所有零件的相似T－Maps进行闵科夫斯基求和(每一个T－Map的所有点的矢量和)获得装配体的累积T－Map，实现装配体的三维公差分析［14］。

1.7 基于SDT的三维公差分析

小位移旋量(Small displacement torsor，SDT)表示带有6个运动分量的刚体产生微小位移所构成的矢量，在1996年由Bourdet等［15］引入到公差领域。与零件的名义尺寸相比其公差一般是相对微小的，零件每个特征的变动量可以用两组矢量精确地描述，即3个旋转矢量和3个平移矢量，这2组矢量即所谓的SDT矢量。

任何机械产品都是由零件装配而成的，零件之间有直接接触的，也有通过运动副连接的。不论是各个零件在加工制造过程中产生的几何误差，还是不同零件之间用运动副连接而形成的误差，在进行装配公差分析时，都必须建立其定量描述。Desrochers等在文献［16］中研究了这些误差的SDT描述方法。基于SDT进行机械装配的三维公差分析要创建三维尺寸链，该尺寸链贯穿装配体的每一个功能要素，这些功能要素对整个装配功能均产生影响。基于SDT的三维公差分析模型为［16］

2 三维公差分析软件

目前主要的三维公差分析软件有:

(1)CATIA.3DFDT 这是由IBM公司发布的公差分析系统。该系统是基于TTRS公差表示模型而开发的，它能协助设计者进行三维公差分析，不过系统仅能处理基于WC模型的三维公差分析问题。

(2)CE/TOL 6 Sigma 这是由美国Rand Worldwide和PTC公司专门发布，是集成于Pro－ENGINEER中的公差分析系统，该系统能进行基于WC、RSS和6 Sigma模型的三维公差分析。

(3)eM－TolMate 该系统由Tecnomatix公司发布。该系统能嵌入大多数 CAD软件(CATIA、Unigraphics、I－deas、Pro－E 和 CADDS5 等)进行三维公差分析，其公差分析是基于Monte Carlo模拟进行。

(4)VSA－GDT/VSA－3D 这2个软件由工程动画公司(EAI)发布，系统能与 CATIA、Unigraphics、I－deas、Pro－E及其它主要CAD系统集成。同eMTolMate一样该系统基于Monte Carlo模拟进行三维公差分析。

(5)3DCS 该软件系统由DCS公司发布，能完全集成于CATIA和Unigraphics，进行三维公差分析使用Monte Carlo模拟法。

上述为目前市场上的主要三维公差分析商业软件，它们能进行包括尺寸公差和几何公差在内的二维和三维公差分析，并且均能集成于主要的商业CAD系统中［18］。其中CATIA.3DFDT有一个好的理论基础，缺点就是在三维装配公差分析中不考虑形状公差。同时，由于零件尺寸变化或形状变化引起的配合零件之间的微小运动学调整而引起的变动不能考虑。与CATIA.3DFDT相比，CE/TOL 6 Sigma功能更为完善，它不仅能执行WC公差分析，也能执行统计公差分析。其他的基于Monte Carlo模拟的公差分析系统需要大量的装配样本来获得一个满意的精确度。

3 三维公差分析技术的研究展望

虽然计算机辅助三维公差分析技术的研究已经取得了较大的发展，但是现有技术处理的大多是某一特定类型的公差问题，有较大的局限性，用来解决工程实际中一般的三维公差分析问题的理论和方法还有待研究。目前，公差分析研究多集中于二维尺寸公差，对于三维公差分析以及与尺寸公差具有同等重要地位的几何公差考虑甚少，迄今为止还没有一种涉及三维几何公差分析的常规方法，尤其是集成于三维CAD系统的尺寸公差和几何公差分析技术更少有研究。新一代GPS已经有较大发展，与新一代GPS标准体系的要求相适应，研究建立满足功能要求及实际测量和评定方法的三维公差数字化的数学模型，开发更具实用性的计算机辅助三维公差分析软件将是未来的重要发展方向。

［1］Desrochers A，Clément A.A dimensioning and tolerancing assistance model for CAD/CAM systems［J］.International Journal of Advanced Manufacturing Technology，1994，9(6):352 －361.

［2］Ameta G，Serge S，Giordano M.Comparison of spatial math models for tolerance analysis:tolerance － maps，deviation domain，and TTRS［J］.Journal of Computing and Information Science in Engineering，2011，11:1－8.

［3］Whitney D E，Gilbert O L，Jastrzebski M.Representation of Geometric Variations Using Matrix Transforms for Statistical Tolerance Analysis in Assemblies［J］.Research in Engineering Design，1994，6:191 －210.

［4］Desrochers A and Rivière A.A matrix approach to the representation of tolerance zones and clearances［J］.International Journal of Advanced Manufacturing Technology，1997，13:630 －636.

［5］Gao J，Chase K W，Magleby S P.Generalized 3－D tolerance analysis of mechanical assemblies with small kinematic adjustments［J］.IIE Transactions，1998，30(4):367 －377.

［6］Wirtz A.Vectorial tolerancing for production quality control and functional analysis in design［C］.Proceedings of the CIRP international working seminar on computer－ aided tolerancing，USA，Penn State，1991:77－84.

［7］Henzold G.Handbook of Geometrical Tolerancing Design，Manufacturing and Inspection［M］.John Willey ＆ Sons，Chichester，1995.

［8］Humienny Z，Johansson G，Kulesza W.Application of vectorial dimensioning and tolerancing to an unique 3 －D stackup analysis［C］.Proceedings of XVII IMEKO World Congress.Croatia，Dubrovnik，2003:1790－1793.

［9］Dantan J Y，Bruyere J，Vincent J P，et al.Vectorial tolerance allocation of bevel gear by discrete optimization［J］.Mechanism and Machine Theory，2008，43:1478 －1494.

［10］Morse E P.Models，representations and analyses of toleranced onedimensional assemblies［D］.PhD thesis，Cornell University ，Ithaca，NY，1999.

［11］Zou Z H，Morse E P.Statistical tolerance analysis using gapspace［C］，7th CIRP International Seminar on Computer Aided Tolerancing，at ENS de Cachan，France，2001:313－322.

［12］Zou Z H.Multi－dimensional tolerance analysis of mechanical assemblies［D］.Ph.D Thesis，University of North Carolina，Charlotte，2003.

［13］Mujezinovic A，Davidson J K，Shah J J.A new mathematical model for geometric tolerances as applied to polygonal faces［J］.Journal of Mechanical Design，2004，126(3):504－518.

［14］Shen Z，Ameta G，Shah J J，et al.A comparative study of tolerance analysis methods［J］.Journal of Computing and Information Science in Engineering，2005，5:247 －256.

［15］Bourdet P，Mathieu L，Lartigue C，et al.The concept of the small displacement torsor in metrology［J］.In Advanced Mathematical Tools in Metrology II，Series on Advances in Mathematics for Applied Sciences，1996，40:110 －122.

［16］Desrochers A，Ghie W，Laperrière L.Application of a unified Jacobian－ torsor model for tolerance analysis［J］.J Comput Inf Sci Eng，2003，3(1):2－14.

［17］Ghie W，Laperrière L，Desrochers A.Re－ Design of Mechanical Assemblies using the Unified Jacobian－Torsor Model for Tolerance Analysis［M］.J.K.Davidson(ed.)，Models for Computer Aided Tolerancing in Design and Manufacturing，2007:95 －104.

［18］Umberto P，Giuseppe G.Overview of current CAT systems［J］.Integrated Computer－Aided Engineering 2002(9):373－387.