MIMO雷达多目标DOA估计

王 磊，隋凯凯，李 宏

（西北工业大学 电子信息学院，陕西 西安 710129）

MIMO雷达多目标DOA估计

王 磊，隋凯凯，李 宏

（西北工业大学 电子信息学院，陕西 西安 710129）

DOA估计是雷达参数估计方面理论研究的一个重要内容，其主要目的是确定各个信号到达阵列参考阵元的方向角。MIMO雷达可以有效提高DOA估计分辨力和精度得到了广泛的关注，但是MIMO雷达DOA估计算法却比较复杂。因此对MIMO雷达DOA估计的几种主要算法进行了深入系统的研究，通过计算机仿真分析比较了各种不同算法的特点，得到了各种算法的优缺点和局限性，从而为正确分析和处理MIMO雷达回波信号提供依据。

MIMO；DOA；参数估计；加权；回波信号

MIMO雷达是基于MIMO技术提出的一种新体制雷达。由于空间分集、波形分集等技术的应用，与传统的相控阵雷达相比，MIMO雷达能够获得更优的目标检测性和参数估计性能。MIMO雷达发射互相正交的波形[1]，在接收端利用发射信号对接收信号进行匹配滤波，从而每个接收信号都可以从中恢复出各发射信号对应的回波。

波达方向估计[2-3]（Direction of Arrival DOA）是利用一组按一定方式布置在空间不同位置的传感器对空间信源在时域和空域同时进行采样，再由传感器阵列采样数据的分析处理来实现对空间信源的方位向估计。MIMO雷达通过发射正交信号，可以扩展阵列孔径；同时增加相互独立的发射和接收阵元的个数，使得收/发天线两两组合成倍产生出更多的有效观测孔径；因此可以有效提高DOA估计分辨力和精度，并可以成倍提高最大可分辨目标数。近几十年，国内外均开展了有关DOA估计技术的理论和应用研究，使得DOA估计理论得到迅速发展。文献[4]指出由于MIMO雷达发射多个独立信号，使得不同目标反射的回波相互独立，因此能够在接收端直接应用Capon自适应处理方法，并给出了Capon算法在MIMO雷达中的应用；文献[5]给出了MUSIC算法在MIMO雷达中的应用；文献[6]给出了Smooth-MUSIC算法在MIMO雷达中的应用；文献[7]给出了Toeplitz-MUSIC算法在MIMO雷达中的应用。

1 MIMO雷达信号模型

设MIMO雷达共有M个发射阵元，发射时沿俯仰方向将发射阵面分成L个子阵（即L个发射通道），每个子阵内的阵元数为M1，M1=M/L。通过对数字收发单元的控制，使各子阵发射信号s1（t），s2（t），…，sL（t）相互正交。 系统有N个发射天线和M个接收天线，接受阵元间距为db倍波长，发射阵元间距为da倍波长。考虑远场一点目标，每个发射天线发射各自的窄带信号波形si（t），i=1，…，N。令从第一个发射阵元到目标处信号的传播时间为τ，则第i个信号从发射到目标处的传播时间 τi=τ+（i-1）daλsin（θ）/c，阵列的发射导向矢量为aθ=[1exp（j2πdasinθ）……exp（j2π（N-1）dasinθ）]r，令ai（θ）为发射导向矢量的第i个元素，i=1，……，N。那么在窄带发射信号的前提下发射到目标的叠加信号为：

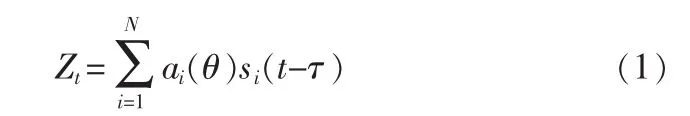
信号zt经过目标反射回到接受阵列，假设目标散射系数为一常数β，则第m个接受阵元的信号为：

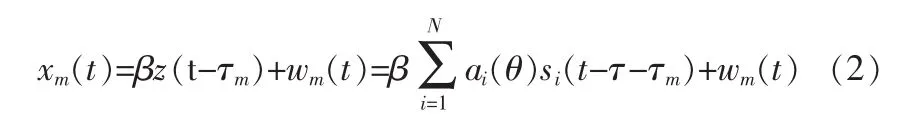
其中wm（t）为第m个接受阵元处的复高斯白噪声，且不同天线之间的噪声不相关。 由于 τi=τ+（i-1）daλsin（θ）/c，同样利用窄带信号的性质，上式（2）则总的接受信号可以写为：

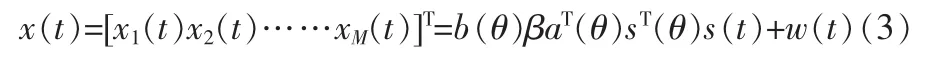
对于存在K目标的情况，接受信号模型为：

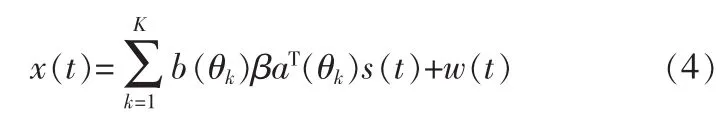
令L为采样点数，上式（4）写成采样的信号模型如下：

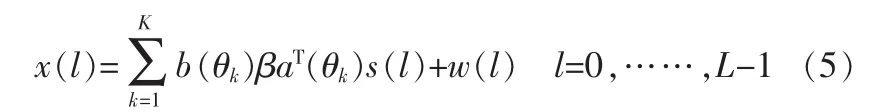
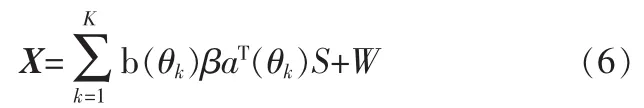
其中X为M行L列的矩阵，L为采样点数。

2 DOA算法

2.1 Capon算法原理

当有多个信号入射传感器阵列时，阵列输出功率将包括期望信号的功率和干扰信号的功率。Capon最小方差法使输出功率最小，从而也使干扰信号的贡献为最小，同时使增益在观测方向保持为常数（通常设该常数为1）。

由于阵列输出为：

其输出信号功率为：

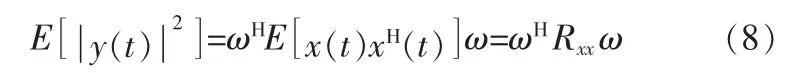
故Capon最小方差法可表示为：

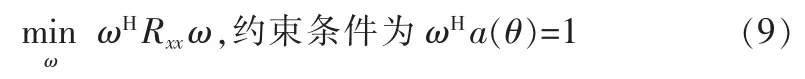
上式是一个约束优化问题，利用拉格朗日乘子法求解得

伊醍酒庄酿酒师Alexandru Luchianov先生则重点推荐了伊醍梅洛2014，该款酒被誉为伊醍酒庄的“红色名片”，是伊醍发展历程中的标志性作品之一，刚刚获得本届Interwine葡萄酒与烈酒大奖赛Premium精品酒双金奖。伊醍酒庄是摩尔多瓦第一家小型精品酒庄，葡萄园和酒厂位于摩尔多瓦东南部的斯特凡沃达产区，这里风土尤为独特，微气候非常适合红葡萄酒的酿制。伊醍的酒彰显的是摩尔多瓦土地的精神的酒，通过酿酒沟通人与自然，沟通人与人。葡萄酒爱好者可以通过微店“醉牛赵先生’s Wine store”购买。

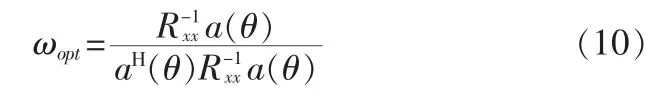
在MIMO雷达系统中，采样数据为接收回波信号通过匹配滤波并进行列堆栈之后的列量，数据协方差矩阵为RYY，MIMO 雷达的导向矢量为 atr（θ）=at（θ）⊗ar（θ）， MIMO 雷达系统的Capon空间谱表达式：

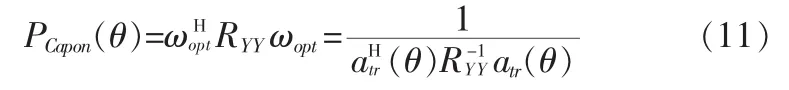
Capon空间谱的谱峰所对应的角度即为所求波达方位角。

2.2 MUSIC算法原理

设一M元等距线阵，阵元间距为d，P（P＜M）个不相关来波信号，噪声为零均值方差σ2n的独立的高斯白噪声，则阵列接受信号可以表示为P个来波信号与噪声的线性组合，即

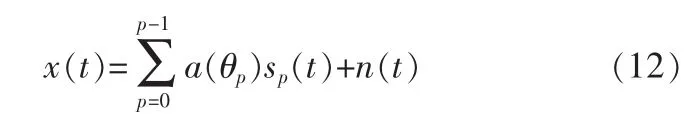
接受信号矢量的协方差矩阵，可表示为：

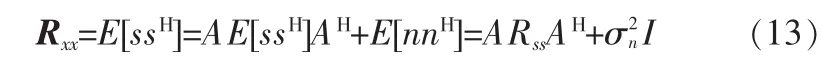
式中，Rxx=E[ssH]是信号自相关矩阵，为噪声方差。

MUSIC空间谱计算公式为：

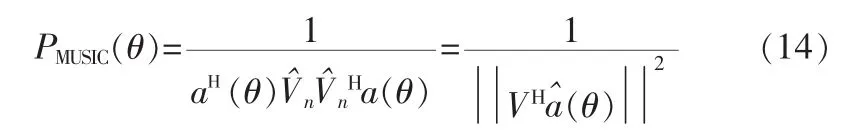
MIMO 雷达的导向矢量为 atr（θ）=at（θ）⊗ar（θ），MIMO 雷达系统的MUSIC空间谱表达式：

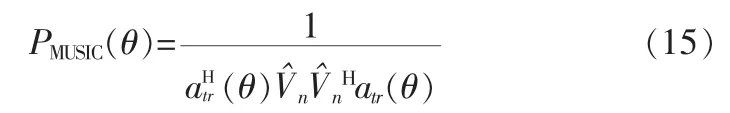
由于噪声的存在，上式中的分母不为零，而是一个很小的值，因此MUSIC空间谱有一个尖峰。使θ变化，通过谱峰搜索来估计到达角。

2.3 Smooth-MUSIC算法

设一个窄带情况下的均匀线阵，第l个阵元接收到的数据为

将均匀线阵（M个阵元）分成相互交错的p个子阵，每个子阵的阵元数为m，即有M=p+m-1。第k个子阵数据模型为

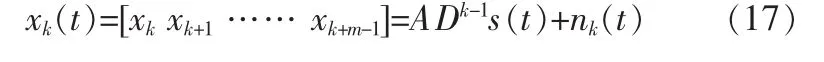
其中

于是该子阵数据协方差矩阵为

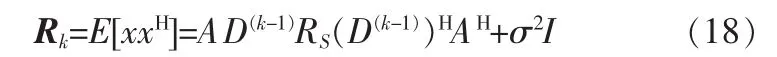
Smooth-MUSIC方法对满秩协方差矩阵的恢复是通过求各子阵协方差矩阵的均值来实现的。即协方差矩阵为

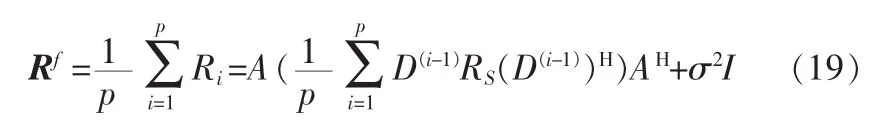
2.4 Toeplitz-MUSIC算法

设阵列输出信号的协方差矩阵为 Rxx=E[xxH]，x（t）=As（t）+n（t） t=1，2…N 。

令I为M×M反向单位矩阵，即

3 算法仿真

实验1针对8阵元均匀线阵，快拍数1 009，3个独立窄带远场，信号阵元间距为λ/2，信号方向角分别设置为0°、5°、20°，信噪比SNR=1。通过MATLAB的仿真实验分析验证4种DOA算法。

由仿真图1～图4[8-9]可以看出，在低SNR的信号背景下，Capon算法、MUSIC算法、Smooth-MUSIC算法以及Toeplitz-MUSIC算法进行DOA估计所得空间谱形状一致，只不过Capon算法的目标分辨率力稍差。

实验2针对8阵元均匀线阵，快拍数1 009，5个独立窄带远场信号，阵元间距为λ/2，信号方向角分别设置为-20°、-10°、0°、10°、20°，信噪 SNR=10。 通过 MATLAB 的仿真实验分析验证4种DOA算法。

由仿真图5～图8[8-9]可以看出，Capon算法与MUSIC算法已经分不清-10°和20°这3个信号，即Capon算法与MUSIC算法在在低SNR以及高相关的信号背景下已经无法分辨。而Smooth-MUSIC算法与Toeplitz-MUSIC算法可以很好地分辨出相干信号。

4 结束语

文中研究了MIMO雷达的基本原理，其中包括MIMO雷达系统结构模型以及信号模型；介绍常用的几种DOA估计方法：Capon算法、MUSIC算法、Smooth-MUSIC算以及Toeplitz-MUSIC算法的基本原理，讨论了这些算法在MIMO雷达中的应用并用MATLAB作了空间谱仿真。对信噪比比较大以及相关比较小的信号，四种算法均能估计出目标方位；但是，对小信噪比信号和到达角度相隔比较近的相干信号，Capon算法与MUSIC算法不能分辨目标，而Smooth-MUSIC算法与Toeplitz-MUSIC算法可以很好地分辨出相干信号。总之，我们对MIMO雷达DOA估计算法的优势和局限性需进一步加强认识，从而在以后的研究中扬长避短，使MIMO雷达的性能进一步提高，并将MIMO雷达的优势充分的在实际应用中体现出来。

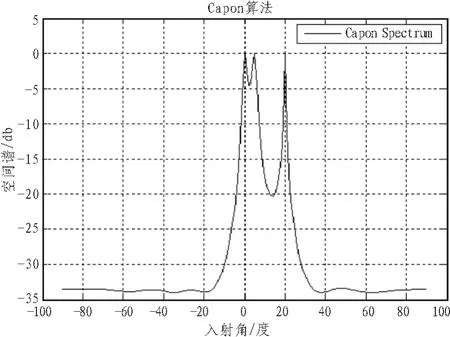
图1 Capon空间谱Fig.1 Spatial spectrum of Capon

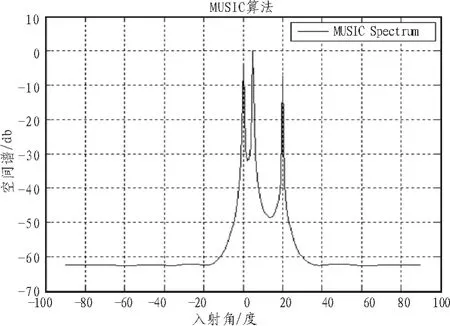
图2 MUSIC空间谱Fig.2 Spatial spectrum of MUSI

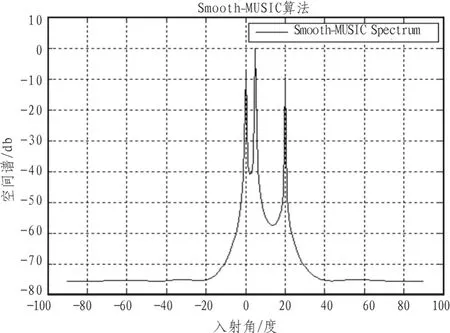
图3 Smooth-MUSIC空间谱Fig.3 Spatial spectrum of Smooth-MUSIC

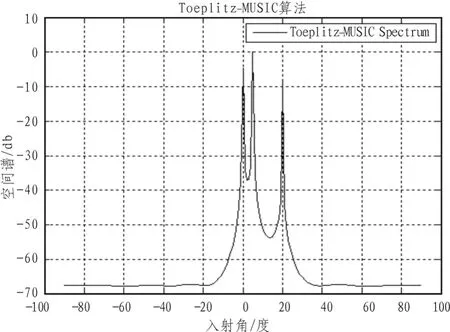
图4 Toeplitz-MUSIC空间谱Fig.4 Spatial spectrum of Toeplitz-MUSIC

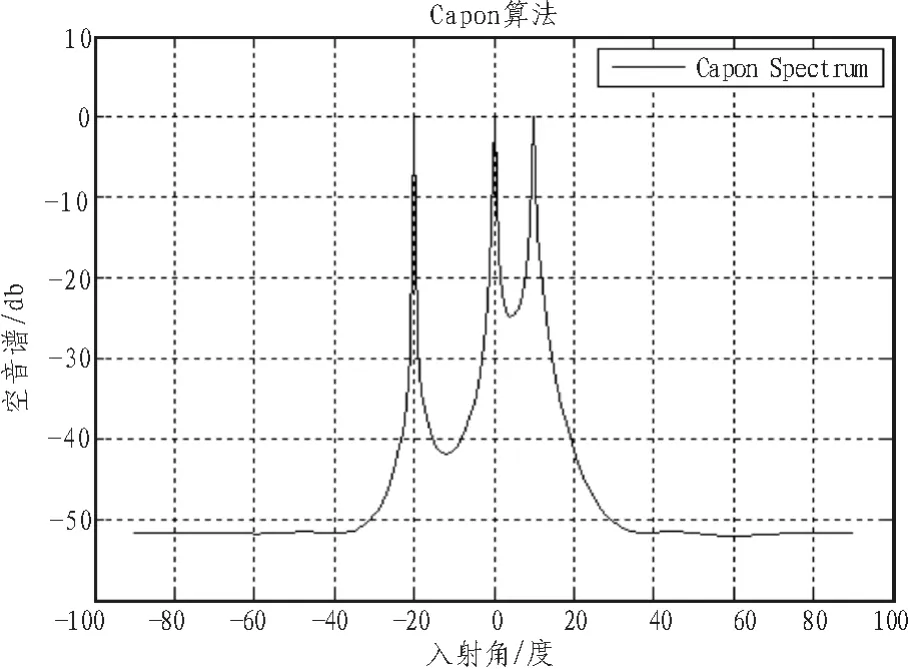
图5 Capon空间谱Fig.5 Spatial spectrum of Capon

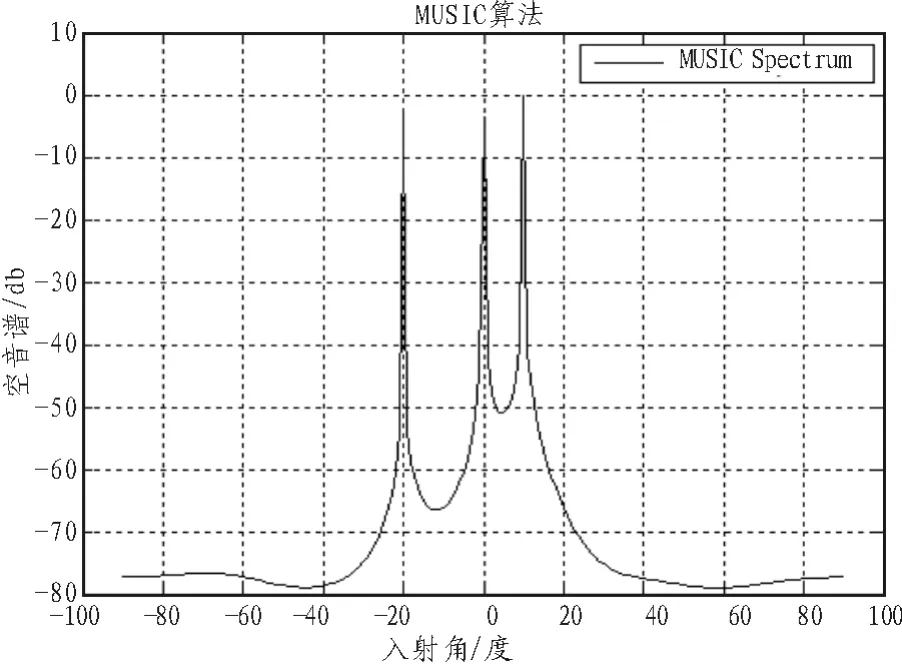
图6 MUSIC空间谱Fig.6 Spatial spectrum of MUSIC

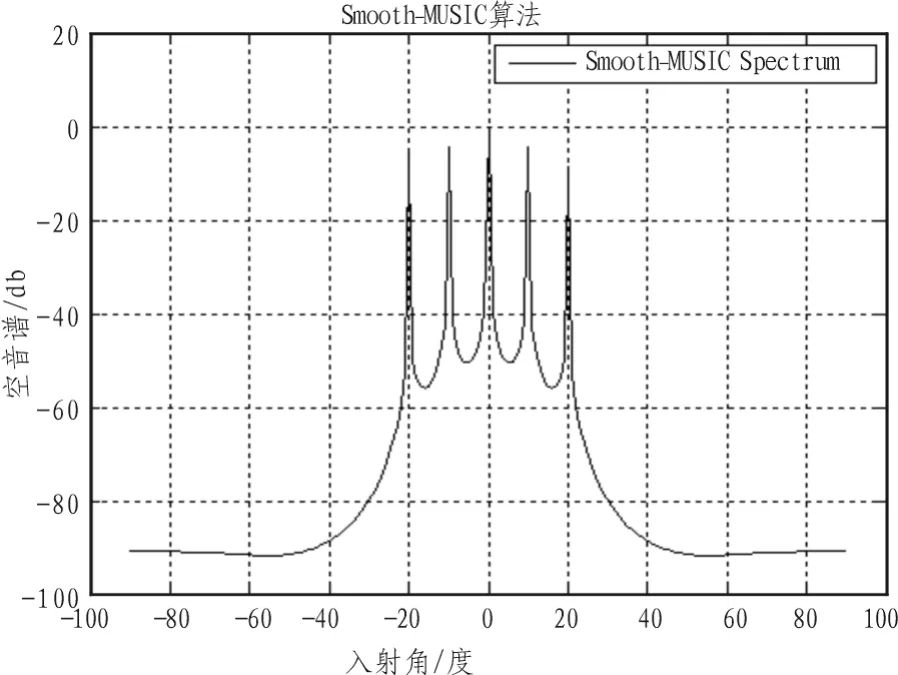
图7 Smooth-MUSIC空间谱Fig.7 Spatial spectrum of Smooth-MUSIC

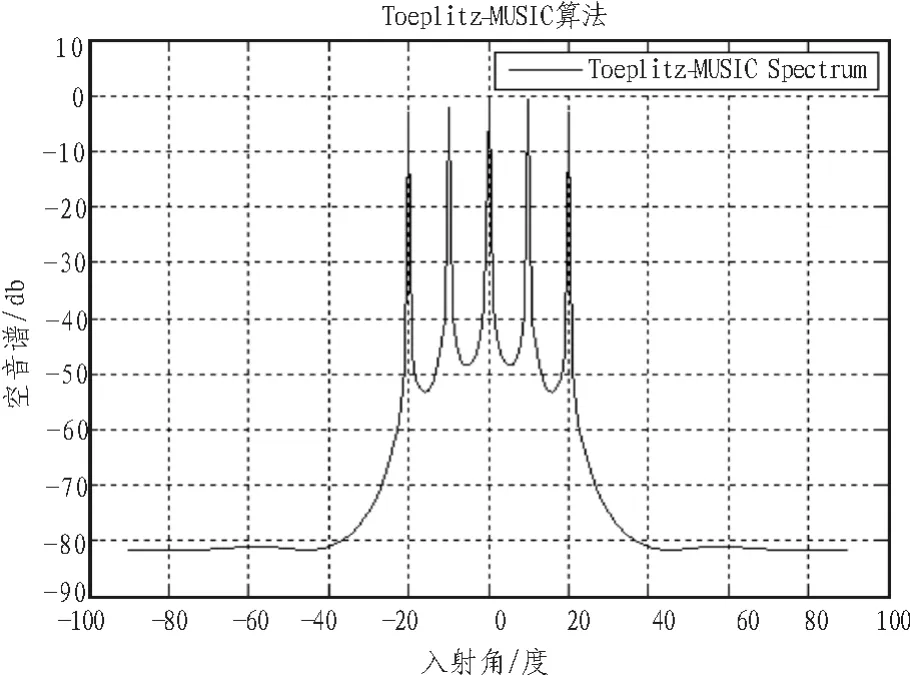
图8 Toeplitz-MUSIC空间谱Fig.8 Spatial spectrum of Toeplitz-MUSIC

[1]明文华，刘志学.一种新体制雷达[J].火控雷达技术，2008，37（1）:10-13.

MING Wen-hua，LIU Zhi-xue.A new radar system[J].Fire Control Radar Technology，2008，37（1）:10-13.

[2]许红波.MIMO雷达DOA估计算法研究 [D].长沙:国防科学技术大学，2009.

[3]杨晓玉.单基地MIMO雷达多目标DOA估计算法研究[D].西安:西安电子科技大学，2009.

[4]王进，赵拥军，王志刚.低信噪比条件下的高分辨DOA估计算法[J].计算机工程，2009，2（4）:96-98

WANG Jin，ZHAO Yong-jun，WANG Zhi-gang. High resolution DOA estimation algorithm with low SNR[J].Computer Engineering，2009，2（4）:96-98.

[5]王艳萍，张志斌，陈娟，等.MIMO雷达DOA估计方法分析[J].电子科技，2010，23（3）:76-80.

WANG Yan-ping，ZHANG Zhi-bin，CHEN Juan，etal.Analysis of the estimation of DOA for the MIMO radar[J].Electronic Science and Technology，2010，23（3）:76-80.

[6]陈小龙，关键，黄勇.DOA估计算法性能分析及仿真[J].海军航空工程学院学报，2009，3（4）:191-194.

CHEN Xiao-long，GUAN Jian，HUANG Yong.Performance analysis and simulation of DOA estimation algorithm[J].Journal of Naval Aeronautical and Astronautical University，2009，3（4）:191-194.

[7]韩勇，乔晓林，金铭.基于Toeplitz矩阵的酉变换波达角估计算法[J].数据采集与处理，2011，26（1）:52-57.

HAN Yong，QIAO Xiao-lin，JIN Ming.Unitary transformation DOA algorithm based on Toeplitz matrix[J].Journal of Data Acquisition and Processing，2011，26（1）:52-57.

[8]杨巍，刘峥.MIMO雷达波达方向估计的性能分析[J].西安电子科技大学学报：自然科学版，2009，10（6）:820-825.

YANG Wei，LIU Zheng.Performance analysis of MIMO radar DOA estimation[J].Journal of Xidian University，2009，10（6）:820-825.

[9]成芳.正交波形MIMO雷达中信号处理与仿真实验研究[D].成都:电子科技大学，2008.

DOA estimation of multi-target in the MIMO radar

WANG Lei， SUI Kai-kai， LI Hong
（Northwestern Polytechnical University，college of Electronics and Information，Xi’an710129，China）

DOA estimation is significant for the theoretical research of the radar parameter estimation，which is used to make sure the direction angle that the signal arriving array elements.It is widely focused on because the MIMO radar can significantly improve the resolution and accuracy of DOA estimation.However，this algorithm is complicated so that it is very hard to process.Based on the several main algorithms of DOA estimation，the author carries out a thorough investigation.By means of the computer simulation，the author analyzes and compares the characteristic of those algorithms.And it provides the basis for analyzing and processing the echo signal of MIMO radar.

MIMO；DOA；parameter estimation；weighted；echo signal

TN913

A

1674－6236（2012）03-0044-04

2011-12-05 稿件编号：201112018

王 磊（1983—），男，陕西宝鸡人，硕士研究生。研究方向：电路与系统。