农村水电站水工建筑物失事概率计算

江 超，盛金保，张国栋

(南京水利科学研究院 水文水资源与水利工程科学国家重点实验室，江苏 南京 210029)

我国现有农村水电站4．5万多座，其中约有1/3的农村水电站水工建筑物部分存在较为严重的病险隐患，安全事故时有发生，造成重大人员伤亡和经济损失，影响国家公共安全与社会稳定［1］．面对农村水电站病险突出的现状，通过引入国外先进理念，对我国面广量大的农村水电站实行风险管理，有助于提升我国农村水电行业的管理水平．

风险由失事概率与失事后果两大要素组成［2］，失事概率的计算既是难点又是重点，正确计算农村水电站失事概率是开展风险管理工作的前提．目前，计算失事概率的常用方法主要有事件树法［3］、历史资料统计法［4］与可靠度方法［5］，但采用这些方法计算农村水电站的失事概率往往很难实现．

一般说来，农村水电站(如不作特别说明，文中的“农村水电站”均特指“农村水电站水工建筑物”)失事概率与运行状态之间存在相关性．运行状态越好，农村水电站失事概率越小;反之，运行状态越差，失事可能性也就越大．避开农村水电站失事概率难于计算的难题，可通过先确定农村水电站运行状态，再利用失事概率与运行状态间的相关性来计算失事概率．

1 运行状态综合评价

农村水电站水工建筑物包括大坝、压力水管、引水渠道、厂房等建筑物，它们自成一个系统，任何一部分运行出现故障都会影响到农村水电站的发电效益．因此，农村水电站运行状态由各组成建筑物的工程性态共同决定．不仅如此，各类水工建筑物的工程性态又受众多因素的影响，如防洪能力、渗流态势、结构稳定性．综合评价方法适合于受多因素多层次影响的问题，因此，选用综合评价方法对农村水电站运行状态展开综合评价．

1．1 综合评价指标体系

指标体系的构建与评价模型的选择是农村水电站运行状态综合评价的关键．综合评价指标应具有代表性、科学性、差异性与可行性［6］．根据农村水电站自身工程特性，选取了与农村水电站运行状态密切相关的13个指标，依次用u1，u2，u3，…，u12，u13表示，具体见图1．

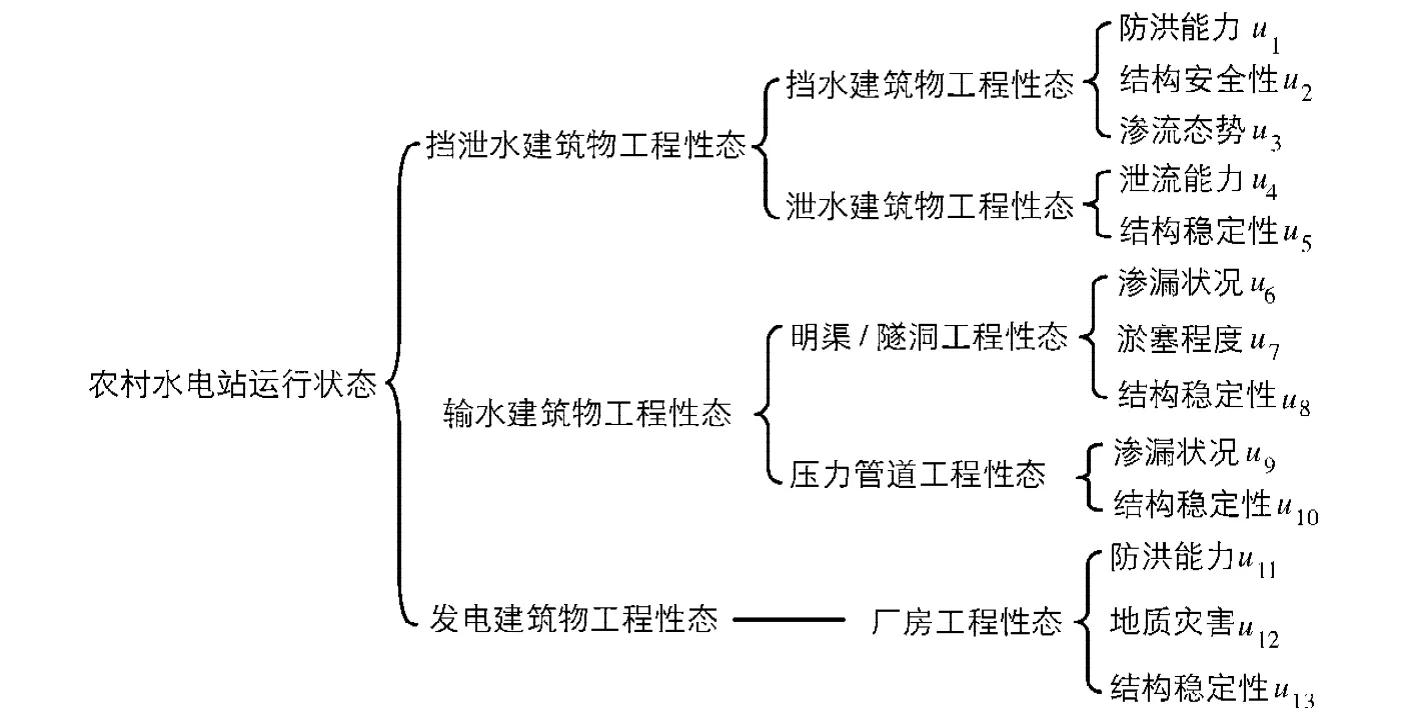
图1 农村水电站水工建筑物运行状态综合评价指标体系Fig．1 Comprehensive evaluation index system for rural hydropower structure operation

1．2 综合评价模型

线性加权综合评价模型综合考虑各指标对整体的影响程度，量化各指标并计入权重后进行叠加，并根据综合评价值确定评价结果［7］．该法适合于对受多因子影响，且各因子影响程度又各不相同的对象进行综合评价．因此，农村水电站运行状态综合评价选用线性加权综合评价模型．

1．2．1 线性加权综合评价模型 农村水电站运行状态的线性加权综合评价模型为:

式中:C为综合评价值;ωi为各指标的权重;¯ui为计入专家权重后的指标计算值．

1．2．2 指标权重 各级指标权重采用层次分析法［8］来确定，层次分析法采用1～9及其倒数作为2个指标重要性比较量化的标度．标度1，3，5，7，9分别表示一个指标与另一个指标相比，同等、稍微、明显、强烈、极端重要的程度，标度2，4，6，8则分别表示上述相邻程度的中间值;2个指标反向对比即为原标度的倒数．农村水电站运行状态综合评价各级指标权重见表1，权重确定主要基于以下几点:

(1)挡泄水建筑物作为整个水工枢纽的核心部分，其工程性态最为关键，输水建筑物与发电建筑物对整个系统的影响则很难分辨．因此，输水类水工建筑物与发电建筑物工程性态“同等重要”，两者之间定为1与1的关系．挡泄水建筑物比输水建筑物“稍重要”，两者之间定为3与1的关系．挡水建筑物与泄水建筑物工程性态介于“稍重要”与“同等重要”之间，定为3与2．

(2)防洪能力作为挡水建筑物最重要的工程指标，其重要程度应高于结构安全性与渗流态势．因此，在影响挡水建筑物工程性态的3个指标中，防洪能力比结构安全性“稍重要”，定为3与1的关系;结构安全性与渗流态势同等重要，定为1与1的关系．同样，泄流能力为泄水建筑物最重要的工程指标，与结构稳定性相比，重要程度应不亚于“稍重要”，两者之间的关系定为3与1．

(3)输水建筑物中，明渠(或隧洞)与压力管道的工程性态重要程度一样，权重各取0．5．在影响农村水电站输水建筑物、厂房工程性态的指标中，各指标对工程性态影响程度相当，指标权重通过平均取值确定．

表1 农村水电站运行状态综合评价各级指标权重Tab．1 Weight of each index of comprehensive evaluation for rural hydropower operation

1．2．3 指标计算值 指标u1，u2，…，u13可分为定性指标、定量指标两类．除挡水建筑物防洪能力、厂房防洪能力为定量指标外，其他均为定性指标．综合评价过程中，需要建立合理的量化标准来量化指标．根据农村水电站自身特点把定性指标分成4个不同的水平等级，定量指标分成4个不同的区间段，4个不同的水平等级或区间段分别打分0～5，5～10，10～15和15～20［9］．各指标对工程性态影响越小，打分值越高，即综合评价值C越大，表明其运行状态越好．

农村水电站运行状态综合评价结果的精确度较大程度上取决于专家打分的合理性与准确性．在对农村水电站运行状态展开评价时，专家组成员多为评价方的主观选择，而且各专家对同一指标的认识程度又不一样，使得专家之间的打分值存在着不同程度的差异．利用传递熵理论可以较大程度上减少专家打分所造成的主观性影响．

(1)传递熵．熵为简单巨系统中的一个重要概念，最早由物理学家R.Clausius于1864年在《热之唯动说》中提出，并用于描述系统的状态［10－11］．传递熵是信息价值与准确度的有效测度．设状态空间x上信息A的条件概率为P(yk，xl)(k，l=1，2，…，n)，A的传递矩阵为E(A)=(e1，e2，…，en)，其中:el(l=1，2，…，n)为状态l发生时信息A的准确度，其值越大，准确度越高．，l=1，2，…，n．称为信息A的传递熵．其中:hk=－eklnek，1/e≤ek≤1;hk=ek≤1/e．传递熵表明了给定信息A的不确定程度．

(2)基于熵的专家评价模型．在给各评价指标打分过程中，假定专家组有一位理想的最优专家，其打分最公正、最准确．以最优专家的打分值为标准，与之相比打分差距越大的专家，其打分精确度就越低，反之精确度越高．与最优专家打分水平的差距用熵来表示，可建立专家评价模型．

设专家组由m位专家S1，S2，…，Sm组成，xij(i=1，2，…，m;j=1，2，…，13)表示第i个专家对第j个评价指标的打分值，向量xi=(xi1，xi2，…，xi13)和矩阵X=(xij)m×13分别表示第i位专家和专家组所有成员的打分情况．设S★为最优专家，其打分向量为x=(x★1，x★2，…，x★13)．用各专家打分向量与S★打分向量的差异大小来评价所选专家的打分水准．专家i的打分水准评价向量为:

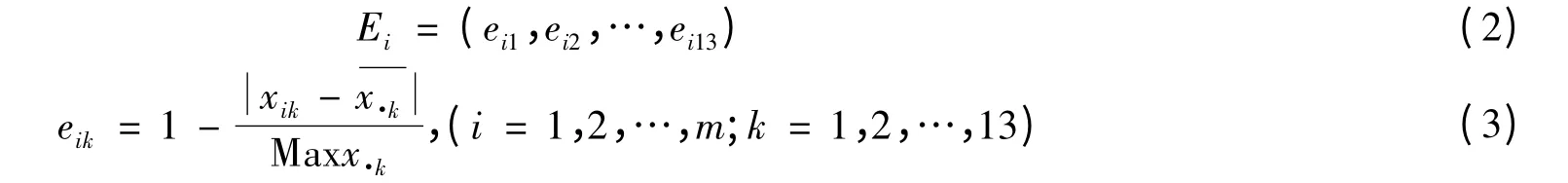
建立的基于熵的专家打分结果评价模型为:

该模型将专家对给定问题的评价能力用打分结果的不确定性来度量，这种不确定性的程度用熵值Hi的大小来表示．熵值Hi越大，表明第i位专家的打分水平越差，越不科学，最后进行加权计算时分配的权重也就越小．因此，可采用式(6)来计算各专家的权重．

采用加权综合的方法对专家们的打分值进行处理，可得出各评价指标计算值¯uj，如式(7)所示．

2 失事概率计算

利用式(8)能近似将运行状态综合评价值C转换为失事概率Pf．

按式(8)计算所得失事概率Pf介于0～1之间，符合概率的数字特征，且满足“运行状态越好，失事概率越小”．采用常规等级划分方法，将综合评价值C的最大值等分成4个区间，对应将农村水电站的失事概率划分成A，B，C，D共4个等级(见表2)．Pf值越大，失事概率等级越高．

表2 农村水电站失事概率等级Tab．2 Level of failure probability of rural hydropower

式(8)计算出的失事概率Pf均较大，与实际情况可能存在一些偏差，但本文的失事概率并无绝对意义，只是相对的概念，用来度量相对失事可能性．

3 工程实例

左湖二级电站坐落于江西省新干县城上乡左湖村，所在河流为赣江水系沂江河，1987年6月投产使用，采用引水式布置形式，总装机800 kW．主要水工建筑物有大坝、溢洪道、引水渠道、压力前池、压力管道、升压站、厂房．配套水库为灌庄水库，集雨面积15．3 km2，总库容229万m3．挡水建筑物为土石坝，最大坝高36．5 m，坝顶长156 m;引水渠道全长约6 km，设计流量0．7 m3/s，实际流量0．6 m3/s;电站设计水头78 m，实际水头78 m．该电站的现状如下:

(1)挡泄水建筑物:配套水库已除险加固完毕，目前挡泄水建筑物工程性态良好．

(2)输水建筑物:渠道险段较多，漏水严重，多处发生过滑坡．衬砌大部分已脱落或已起不到防渗作用，只针对性地对某些漏水严重渠段重新进行了衬砌，泥沙淤积异常．渠道上方山体岩石裸露，风化碎石坠落于渠道中，影响渠道过流能力，甚至会造成堵塞;压力前池严重老化，池身裂缝多，漏水量大，池内淤积泥沙亟需清理;压力管道于2007年进行了更新，无漏水现象，结构保持稳定．

(3)厂房:建于1986年，设施简陋，但整体结构完好，墙面仅部分地方出现轻微剥落，未见影响结构安全的裂缝;厂房后山体边坡进行了抗滑处理．

(4)管理水平:电站的管理人员均为当地农民，没有经过正式培训，无上岗证，专业知识比较薄弱;有日常运行、巡查、操作与设备缺陷记录，且资料保存完好．

现有6人组成的农村水电站风险评价专家小组，在了解左湖二级电站相关情况之后，各专家按指标打分标准［9］分别独立地给13个风险指标打分，6位专家分别用S1，S2，S3，S4，S5，S6表示，并基于专家评价模型原理计算专家权重(见表3)．

将ci代入式(7)计算计入6位专家权重后的各指标值分别为:¯u1=17．24，¯u2=17．38，¯u3=17．12，¯u4=13．71，¯u5=16．75，¯u6=2．99，¯u7=2．33，¯u8=3．76，¯u9=17．23，¯u10=17．80，¯u11=12．08，¯u12=13．48，¯u13=13．02．将所得计算值代入式(1)和(8)，计算得农村水电站运行状态综合值C和失事概率Pf分别为14．317和0．284．按表2对农村水电站失事概率进行等级划分，左湖二级电站失事概率属于B级，运行状态一般，失事可能性不大，与“配套水库已除险加固完毕”的实际情况一致，一定程度上验证了该方法的正确性与合理性．

4 结语

本文提出利用农村水电站失事概率与运行状态的相关性，通过综合评价农村水电站运行状态来反求其失事概率．将该方法应用到江西省左湖二级电站失事概率计算中来，所得结论合理，取得了不错的效果．

综合评价中专家打分所带来的主观性影响难以避免，采用专家评价模型对专家们的打分结果进行处理，可以大大地减轻主观性所造成的影响，使农村水电站运行综合评价结果更趋合理，决策更具科学性．

各指标的量化标准直接关系到打分的准确性．指标量化标准是否完善，是否足够细化，是否界限分明，还需要在日后实际运用过程中检验，同时，在使用过程中指标量化标准也需要不断地细化、完善与补充．

［1］水利部农村水电及电气化发展局．中国小水电60年［M］．北京:中国水利水电出版社，2009．(Rural Hydropower and Electrification Development Bureau，Ministry of Water Resources．60 years of small hydropower in China［M］．Beijing:China Waterpower Press，2009．(in Chinese))

［2］郭仲伟．风险分析与决策［M］．北京:机械工业出版社，1987．(GUO Zhong-wei．Risk analysis and decision［M］．Beijing:China Machine Press，1987．(in Chinese))

［3］金朝光，林焰，纪卓尚．基于模糊集理论事件树分析方法在风险分析中应用［J］．大连理工大学学报，2003，43(1):97-99．(JIN Chao-guang，LIN Yan，JI Zhuo-shang．Application of event tree analysis based on fuzzy sets in risk analysis［J］．Journal of Dalian University of Technology，2003，43(1):97-99．(in Chinese))

［4］李雷，王仁钟，盛金保，等．大坝风险评价与风险管理［M］．北京:中国水利水电出版社，2006．(LI Lei，WANG Renzhong，SHENG Jin-bao，et al．Dam risk evaluation and risk management［M］．Beijing:China Waterpower Press，2006．(in Chinese))

［5］张明．结构可靠度分析［M］．北京:科学出版社，2009．(ZHANG Min．Structural reliability analysis［M］．Beijing:China Waterpower Press，2009．(in Chinese))

［6］朱党生，张建永，廖文根，等．水工程规划设计关键生态指标体系［J］．水科学进展，2010，21(4):560-566．(ZHU Dang-sheng，ZHANG Jian-yong，LIAO Wen-gen，et al．A key ecological indicator system for water project planning and design［J］．Advances in Water Science，2010，21(4):560-566．(in Chinese))

［7］张会，张继权，韩俊山．基于GIS技术的洪涝灾害风险评估与区域研究［J］．自然灾害学报，2005，14(6):141-145．(ZHANG Hui，ZHANG Ji-quan，HAN Jun-shan．GIS-based assessment and zoning of flood/waterloging disaster risk［J］．Journal of Natural Disasters，2005，14(6):141-145．(in Chinese))

［8］汪应洛．系统工程［M］．北京:机械工业出版社，2008．(WANG Ying-luo．Systems engineering［M］．Beijing:China Machine Press，2008．(in Chinese))

［9］江超．小水电水工建筑物风险分析［D］．南京:南京水利科学研究院，2011．(JIANG Chao．Risk analysis of hydraulic structure for small hydropower［D］．Nanjing:Nanjing Hydraulic Research Institute，2011．(in Chinese))

［10］张殿祜．熵—度量随机变量不确定性的一种尺度［J］．系统工程理论与实践，1997，(11):1-3．(ZHANG Dian-hu．Entropy-a scale of measuring random uncertainty［J］．Systems Engineering-Theory and Practice，1997，(11):1-3．(in Chinese))

［11］余建星，李彦苍，吴海欣，等．基于熵的海洋平台安全评价专家评定模型［J］．海洋工程，2006，24(4):90-93．(YU Jian-xin，LI Yan-cang，WU Hai-xin，et al．Specialists selection model for safety assessment of offshore platforms based on entropy［J］．The Ocean Engineering，2006，24(4):90-93．(in Chinese))