地震作用下高桩承台桥梁结构工程简化模型的研究与分析

李洞明

（上海市政工程设计研究总院（集团）有限公司，上海市 200092）

1 概述

随着经济的飞速发展，大量桩基桥梁纷纷建造，而地震灾害也在世界各地频繁地发生，桥梁震害已经引起了人们的重视，因此有必要对在地震作用下土层中桩基础的地震响应以及考虑桩土相互作用的上部结构地震响应的计算方法进行研究分析。由于Penzien模型形式比较简单，也基本能够反映地震荷载和土层对桩基和结构的影响，因此目前考虑桩土相互作用的桥梁结构抗震分析中常采用Penzien模型。尽管Penzien模型比较简单，但在实际工程计算中仍然繁琐。在实际工程中，为了建模和计算方便，经常用如下简化来考虑桩土相互作用：对于高桩承台结构，在冲刷线以下－定深度处固结，然后输入某一地震动作为激励；对于低桩承台结构，经常采用6个弹簧（Kx，Ky，Kz，Kθx，Kθy，Kθz）来模拟基础，输入冲刷线处的地震动作为激励。经过实际的应用和分析，低桩承台结构的这种工程简化模型具有较好的精度[1]，故本文将重点讨论如何建立高桩承台结构的工程简化模型，即在何处固结，以及输入何处地震动作为激励。

为了确定简化模型的固结位置和地震动输入，本文主要进行了如下工作：分析自由场地中场地土的地震响应；采用Penzien模型分析影响上部结构地震响应的因素；提出固结位置的确定方法，并讨论了土弹簧的计算方法；最后用Penzien模型对工程简化模型进行了校核。

2 自由场地的地震响应

在高桩承台结构的工程简化模型中，需要确定固结点处的地震动输入，故本文对工程场地的地震响应进行分析。

本文采用的工程场地的土层性质如下：20m厚分层非线性土场地，此场地属于Ⅲ类场地土，具体分层见图1。

图1 场地的土层分布情况

基岩采用的地震动输入为对应于Ⅲ类场地的1940 ElCentro波，加速度峰值分别采用0.2g和0.5g，其加速度峰值为0.2g时时程曲线见图2。

图2 1940 El Centro波加速度时程曲线

对以上土层采用不同加速度峰值地震波作为激励进行计算，土层中位置0m、-1m、-2m、-3m、-4m和-5m的加速度时程见图3、图4。

从图3、图4可知：在地震作用下，地表以下一定范围内土体的性质相近时，其加速度峰值和振动的频谱特性基本相同。因此在采用工程简化模型的时候，若在地表附近的土体性质相近时,可以采用地表的地震响应作为激励输入模型。

图3 1940 EL Centro波、加速度峰值0.2 g时土层中各位置的加速度时程

图4 1940 EL Centro波、加速度峰值0.5 g时土层中各位置的加速度时程

3 对影响上部结构地震响应的因素的探讨

结构的地震响应主要由结构本身的振动特性和结构所受的地震激励所决定，以下本文将改变Penzien模型中的结构自振特性和地震激励来研究上部结构的地震响应，具体做法如下：（1）结构自振特性的改变，把Penzien模型中的桩长进行改变，在桩底处固结，并输入相应位置处土层中的地震动，桩身其余位置仍用弹簧－阻尼单元来考虑桩和土的连接（见图5）；（2）地震激励的改变，根据以上分析，地表附近土中的地震响应基本接近，故在Penzien模型中一致输入地表处的地震动（见图6）。

本文对多个工况进行了上述的计算，采用的结构型式、场地和地震激励描述如下：

（1）结构型式见图7、图8，通过改变桩的自由长度L2和桥墩高度L1来实现结构型式的改变；

图5 改变桩长的Penzien模型

图6 一致输入地表处的地震动的Penzien模型

图7 高桩承台结构立面布置图（单位：m）

图8 高桩承台结构平面布置图（单位：m）

（2）工程场地，采用上文中工程场地（见图1）；

（3）地震动，将不同场地受加速度峰值为0.2g、0.3g和0.5g的 1940 EL Centro波激励后的地震响应施加到结构上。

经计算，各个工况的墩底弯矩见表1。

从表1可以得出：（1）改变Penzien模型中的地震动输入，即将输入各土层位置的地震动改为一致输入地表处的地震动，得出的上部结构的地震响应非常接近；（2）改变Penzien模型中桩基础的长度，即改变了桩基子结构的动力特性，得出的上部结构的地震响应相差较大。这些说明了表层土的地震响应和桩基子结构的动力特性对上部结构的地震响应影响较大，因此在寻找恰当的桩基结构工程简化模型的时候尤其需要注意的就是这两点。通过以上的论述，可知在地表附近的土体性质相近时可以采用地表的地震响应作为激励输入简化模型，在大多数情况下地表的土性都相同，故在大多数情况下可以将地表的地震动作为简化模型的激励。

表1 1940 EL Centro波在不同地震强度和结构型式下墩底的地震响应

4 高桩承台结构工程简化模型的固结位置的确定

在给定的地震动激励下，结构的地震响应由结构本身的特性所决定，因此工程简化模型中只要选择恰当的固结位置，使桩基结构的水平抗推刚度与Penzien模型一致，那么它们的振动特性中对水平向地震响应起控制作用的振动特性均相同，故它们的地震响应也基本一致。因此固结位置由桩基结构水平刚度等效的原则确定，可按式（1）计算。

式（1）中：K——整个桩基结构的抗推刚度,N/m；I——桩的抗弯惯矩之和，m。

从式（1）中可见，只要求出桩基结构的水平抗推刚度K，然后按照式（1）求出等效的桩长L，就实现了Penzien模型到工程简化模型的转化，见图9、图10。下文将对计算桩基水平抗推刚度时所需的土弹簧的计算方法进行探讨。

土弹簧刚度的确定，除考虑使用较为精确的有限元或边界元方法外，较为简便的方法是采用Penzien模型中提供的土弹簧计算方法或参照现行规范中土弹簧的计算方法。

Penzien模型将桥梁上部结构多质点体系和桩-土体系的质量联合作为一个整体，来建立整体耦联的地震振动微分方程组进行求解。该模型假定桩侧土是Winkler连续介质。以半空间的Mindlin静力基本解为基础，将桩-土体系的质量按一定的厚度简化并集中为一系列质点，离散成一理想化的参数系统，并用弹簧和阻尼器模拟土介质的动力性质，形成一个包括地下部分的多质点体系。

Penzien模型中提供的土弹簧计算方法可以反映地震波的频率特性和强度对土弹簧的影响，但是这种方法需要土参数较多，而且计算过程比较复杂，不便于实际应用。我国《公路桥涵地基与基础设计规范》(JTJ024-85)用的m法在计算方法和参数选取方面比Penzien的方法要简单和方便，且为国内广大工程师所熟。但是，由于桩上相互作用的实验数据不足，土的物性取值有时亦缺乏合理性，在确定土弹簧的刚度时，仍有不少问题未能很好解决。特别是，m法中m的取值对弹簧刚度的计算结果影响很大，且不能反映地震波的频率特性和强度对土弹簧的影响。

孙利民教授曾对m法和Penzien方法计算土弹簧刚度的结果进行了对比分析[2]。计算实例为日本神户的一座钢筋混凝土三跨连续梁桥的单墩桥梁基础。他发现如果恰当取值可以使两种方法算得的结果较好地符合。但是由于桥规中给出的m取值范围很大，m的取值会对计算结果产生很大的影响。孙利民教授建议工程技术人员进行抗震设计与分析时，有必要根据地震波的类型、大小恰当选取m值，来计算等效土弹簧刚度，以期与实际地震作用时的情况相符。为了校验用m法计算土弹簧的适用性，以下对采用Penzien方法和m法计算土弹簧和结构的地震响应进行比较（见图1 1、表2），在采用m法计算时m值取2倍的《公路桥涵地基与基础设计规范》(JTJ024-85)表中的大值。其中，Kp为采用Penzien方法计算的土弹簧刚度，Km为采用m法计算的土弹簧刚度。

图11 1940 EL Centro波，不同加速度峰值下Kp/Km随深度变化图

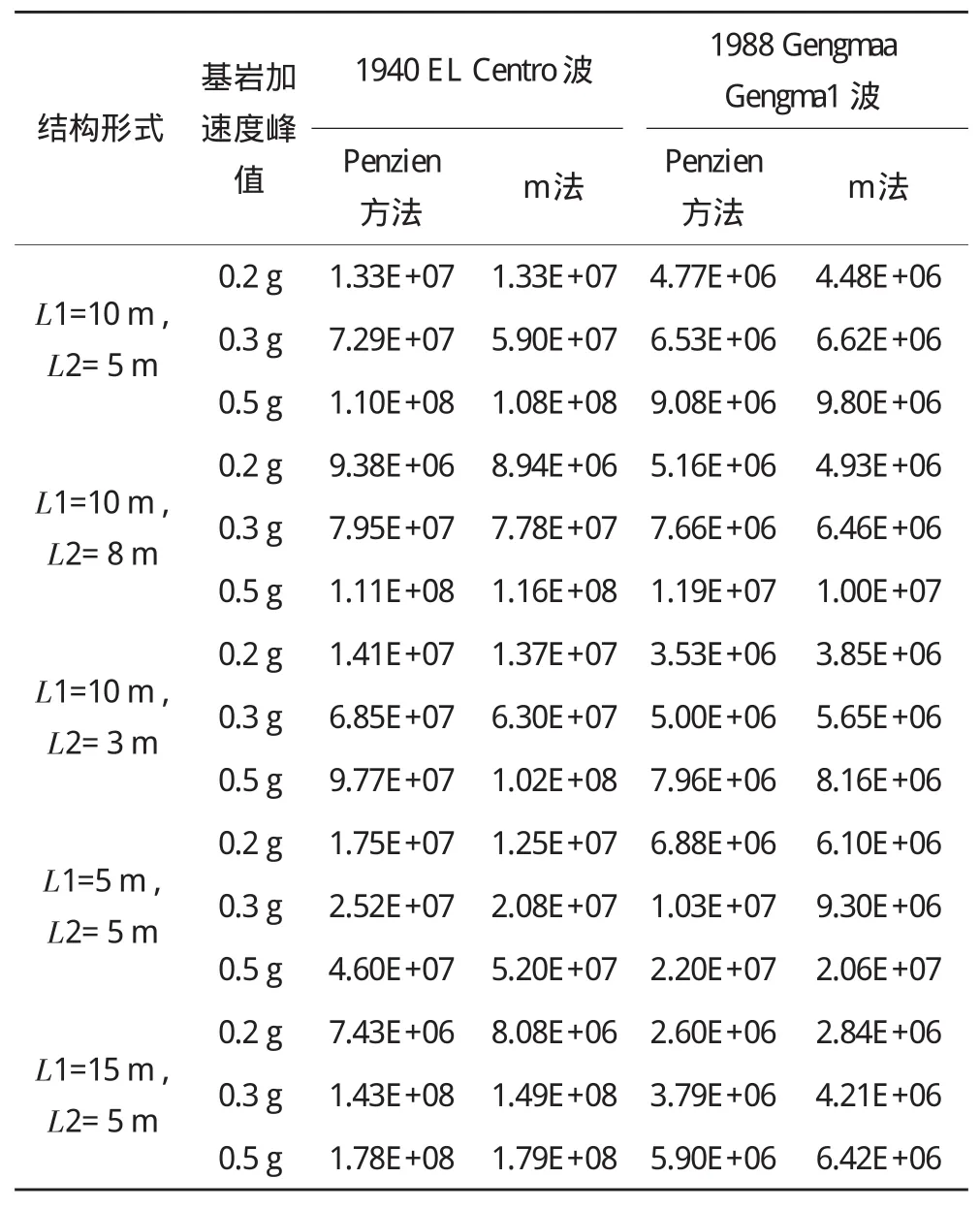
表2 采用不同方法计算土弹簧时墩底弯矩（单位：N·m）

从图11以及表2可知，采用Penzien方法和m法计算的土弹簧刚度有所不同，但是计算出的结构响应能比较接近，可见m法还是有着一定的适用性。

5 算例

以下将采用上述的高桩承台结构简化模型来计算结构，工程简化模型的计算步骤如下：

（1）将群桩合并成单桩，并桩后合成截面的面积为原群桩中各桩面积之和，合成截面的抗弯惯性矩为原群桩中各桩抗弯惯性矩之和，合成截面的抗扭惯性矩为原群桩中各桩抗扭惯性矩之和；

（2）按照m法求出土弹簧刚度；

（3）把土弹簧施加在并桩后的桩基上，计算桩基的抗推刚度，按照式（1）求出等效桩长；

（4）按照以下公式计算承台上的抗弯和抗扭弹簧:

式

（2）中：kφx——抗弯力矩，N·m;

xi——第i根单桩轴线距承台中心距离在x方向上的投影,m；

A——单桩的面积,m2；

E——桩的弹性模量,Pa；

l——承台底距桩嵌固端的距离,m。

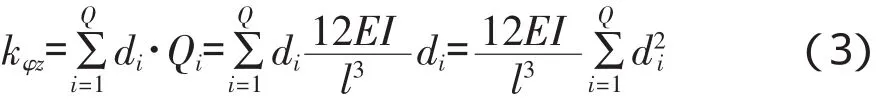
式（3）中：kφz——抗扭力矩，N·m;

di——第i根单桩轴线距承台中心的距离,m；

I——桩的转动惯量,m4。

（5）建立结构的计算模型，桩基部分用第3步中得出的一定长度的桩来代替，桩底固结，将第4步中计算的抗弯抗扭弹簧施加到承台上；

（6）在桩底固结位置处输入地表处的地震动计算上部结构在水平地震荷载下的响应。

为了校验工程简化模型的适用性，对它的计算结果用Penzien进行校核，Penzien模型的地震输入分为两种情况，即输入各土层的地震动和输入地表处地震动，工程简化模型输入地表处的地震动。Penzien模型的土弹簧刚度计算采用Penzien方法。

本算例采用的是某一主跨730m的双塔钢斜拉桥，钻石形桥塔，跨径布置为：110m+240m+730m+240m+110m。桥面宽度为34m（不计入风嘴的宽度），主梁为封闭钢箱梁，梁高为3.5m,梁宽34m。主通航孔边跨采用压重，其中辅助墩处压重1300t，边墩压重1000t。采用平行钢丝斜拉索，标准索距15m。主塔基础采用52根Φ2.5～3.2m的变直径钻孔灌注桩基础，桩长104m，桩身上部40m段直径为3.2m，下部64m段直径为2.5m，桩的混凝土标号为30号，在冲刷线以上桩长16m。承台底面标高为-1.0m，厚5m，上有棱台形塔座。辅助墩和边墩均采用分离式的薄壁箱形空心墩，平面尺寸为7m×5m，墩柱壁厚70cm，边墩高约45.5m，辅助墩高约48m。墩身采用40号钢筋混凝土。辅助墩基础和边墩基础分别采用18根和12根Φ2.5～3.2m的变直径钻孔灌注桩基础，桩长80m，桩身上部40m段直径为3.2m，下部40m段直径为2.5m，桩的混凝土标号为30号，在冲刷线以上桩长1 4m。承台底面标高为0.0m，厚3.5m。总体布置见图12。

结构所处场地为多层非线性土场地，详细土层情况见表3。

表3 场地土资料

基岩采用的地震动输入为1988 Gengmaa Gengma 2波，加速度峰值分别采用0.2g、0.3g和0.4g，其加速度峰值为0.2g时时程曲线见图13。沿纵桥向输入。

计算结果见表4～表6。

在表4～表6中，工程简化模型的计算结果和输入地表处地震动的并桩Penzien模型结果很接近，与输入各土层地震动的并桩Penzien模型相比偏小，但是仍比较接近。可见当表层土性质接近时，可以用地表处的地震动作为激励计算上部结构的地震响应，并且工程简化模型也具有较好的精度。

图12 总体布置图（单位：m）

图13 1988 Gengmaa Gengma2波加速度时程

表4 基岩加速度峰值为0.2 g时结构各位置的内力

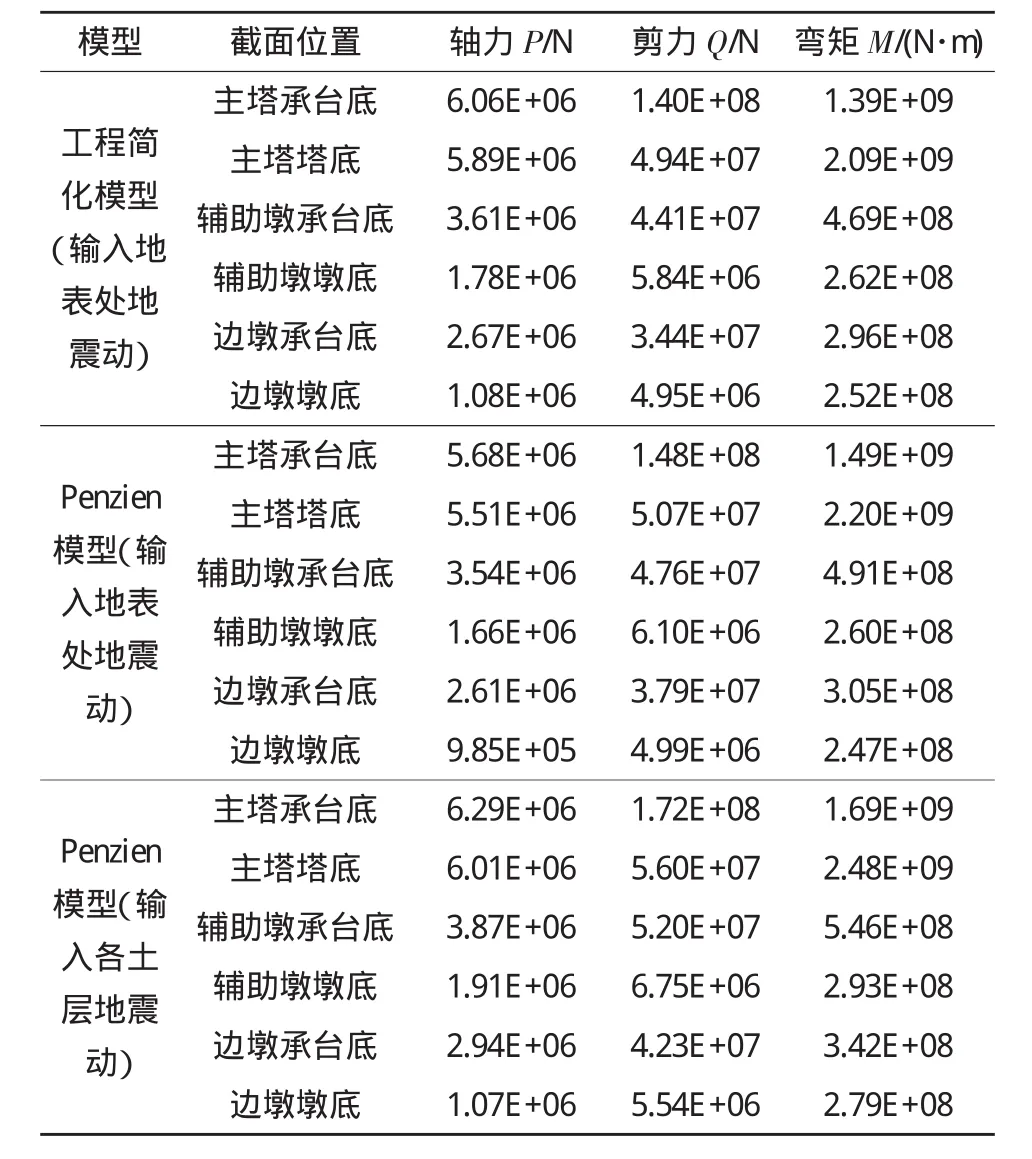
表5 基岩加速度峰值为0.3 g时结构各位置的内力

表6 基岩加速度峰值为0.4 g时结构各位置的内力

6 结语

本文主要论述了高桩承台结构工程简化计算模型中固结位置和输入地震动的确定方法，为此，对自由场地地震响应、影响上部结构地震响应的因素、土弹簧的计算方法进行了探讨，并且最后用Penzien模型对工程简化模型进行了计算核对。通过计算实例的验算，表明了工程简化模型具有良好的精度，表明了本文所述的按照水平抗推刚度确定固结位置，以及在地表土层性质相近时采用地表处地震动作为激励计算上部结构的地震响应是合适的。

[1]陆锐.群桩桥梁结构抗震简化计算方法的比较分析[D].上海：同济大学，2001.

[2]孙利民.桩基桥墩的非线性地震反应分析[A].第25届日本地震工学研究发表会论文集（日文）[C].东京：日本土木学会，1999.