宏观偏析数学模型在大型钢锭中的应用
李文胜 沈厚发 柳百成(.广东电网公司电力科学研究院,广东50080;
2.清华大学机械工程系先进成形制造教育部重点实验室,北京100084)
高质量大型钢锭的生产是我国装备制造业发展面临的重要问题[1、2]。大型钢锭特别是百t级以上特大型钢锭中的一个重要质量缺陷是宏观偏析。宏观偏析是指凝固过程中由于溶质再分配、流体流动、自由等轴晶移动等因素所导致的宏观尺度上的化学成分分布不均。大型钢锭的凝固过程和宏观偏析的形成是一个多相多尺度的问题,涉及热溶质对流、凝固收缩以及等轴晶移动等诸多复杂因素[3、4]。传统的连续模型不能满足建模的要求,两相/多相模型能够更好地描述实际钢锭凝固过程中的质量、动量、能量和溶质的宏观传输及微观尺度上发生的凝固现象。
本文介绍了宏观偏析数学模型的发展以及在实际钢锭中的应用。值得注意的是,由于文献报道的宏观偏析模拟和实验研究所采用钢锭的尺寸特点,本文主要讨论3 t以上钢锭的研究。
1 宏观偏析数学模型简介
1987年,Bennon和Incropera[5]采用经典的混合物理论,建立了描述二元凝固体系动量、能量和溶质传输的连续模型。该模型将固相区、糊状区和液相区视为一种连续介质,对这3个区域的传输过程采用同样一套守恒方程来描述。糊状区被视为具有宏观特性的固-液混合物,固相和液相几乎同时,Beckermann和Viskanta[6]发表了二元合金凝固宏观偏析体积平均模型。在一个小的体积单元内对各相微观守恒方程进行积分,获得体积平均的各相宏观守恒方程。在各相宏观守恒方程中,微观的固-液界面的存在是以界面传递项的形式得到体现的。将固相和液相宏观守恒方程叠加,利用界面平衡关系去掉方程中的界面传递项,获得固-液混合物的一套宏观守恒方程(质量、动量、能量和溶质方程)。因此,该模型也采用一套守恒方程描述固相区、液相区和糊状区。
合金凝固体系包括液相和固相,而上述模型并没有建立固相动量守恒方程。事实上,凝固过程中形成的固相自由等轴晶颗粒在熔体中发生宏观运动,等轴晶的漂浮或沉降对宏观偏析的形成具有重要影响。1991年,Ni和Beckermann[7]建立了合金凝固传输过程的体积平均两相模型。与以往模型不同的是,该模型针对液相和固相分别建立一套宏观传输方程。通过界面交互关系,将两相的质量、动量、能量和溶质守恒方程紧密联系起来,同时将微观凝固现象耦合到宏观传输模型中。通过适当的处理方式,该模型可以考虑宏观尺度上的传热、溶质再分配、熔体对流和等轴晶移动以及微观尺度上的形核、过冷和晶粒生长机制。最近,Combeau等人[8、9]提出了考虑等轴晶移动的两相/多尺度模型,Ludwig等人[10、11]开发了较为复杂和完善的多相模型。
2 宏观偏析数学模型在实际钢锭中的应用
2.1 连续模型和体积平均模型
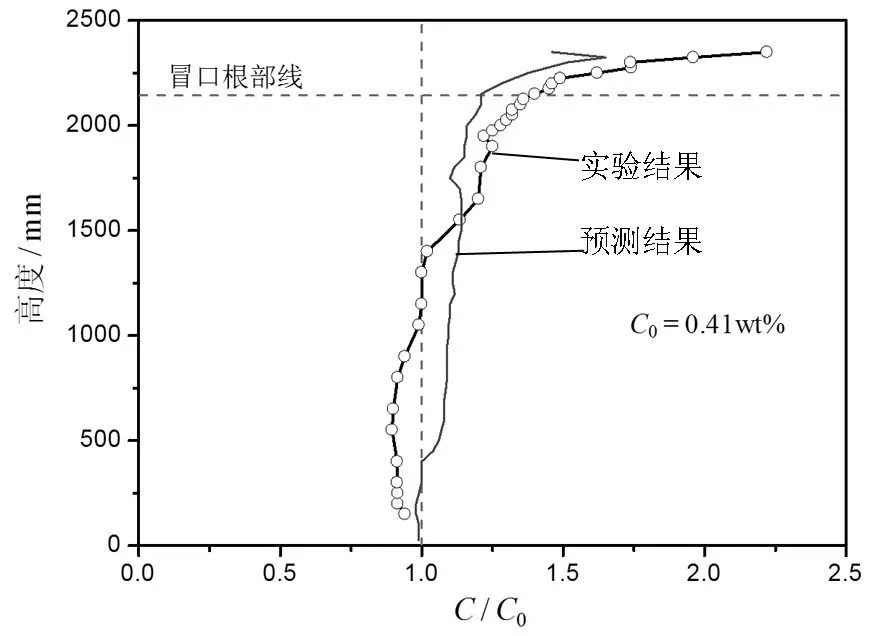
从1990年开始,Combeau等人[12、13]提出采用考虑热溶质对流作用的多组元合金凝固模型,预测了工业钢锭的宏观偏析(二维模拟)。该模型类似于Beckermann和Viskanta[6]建立的二元合金体积平均模型,对于多组元的考虑则体现在动量守恒方程浮力项的改变,即在浮力项中引入了不同合金元素对溶质浮力及溶质对流的影响。模拟了6.2 t钢锭的凝固过程,计算中考虑了8种合金元素,将预测的宏观偏析结果与实验结果进行了比较[13]。针对65 t钢锭的凝固过程进行了模拟。图1所示为钢锭中心线上的碳成分偏析预测结果与实测的比较[4、12]。图1中,名义成分C0= 0.22%,Hmax=3.8 m。在钢锭底部区域(H/Hmax< 0.2)和顶部区域(H/Hmax> 0.75),预测结果与实测结果吻合较好。在钢锭中部区域(0.2 1999年,Gu和Beckermann[14]采用体积平均模型模拟了工业规模的大钢锭(高约2.55 m,重约43 t)的凝固过程。模型考虑了热溶质对流,并处理了凝固收缩和冒口缩孔的形成。考虑了11种合金元素及不同合金元素的偏析特征对液相密度的影响。采用了二维模拟,网格数为38×54。由于涉及多组元全耦合计算,计算所用CPU时间长达数周。图2所示为钢锭中心线碳成分偏析预测结果与实测的比较。可见,预测与实测表现出基本相同的趋势。然而,在钢锭下部区域(H< 1 500 mm),预测的碳含量高于实测值。在钢锭上部区域(H> 1 500 mm),预测的碳含量低于实测值。该模型没有能够有效地预测到钢锭底部实测的负偏析,导致这一误差的主要原因是模型没有考虑等轴晶的移动。 2007年,Bellet等人[15]采用体积平均模型预测了热溶质对流作用下的宏观偏析形成。为实现模型的数值求解,提出了自适应的各向异性网格重构方法。针对凝固前沿附近液相速度梯度较大的关键区域,采用局部细化的网格。对重约3 t钢锭的凝固过程进行了二维模拟,预测了钢锭中的宏观偏析。 在国内,1995年,顾江平[16]对连续模型进行了修改,建立了多组元低合金钢凝固模型。在Fe-C二元合金连续模型的动量方程浮力项中引入其它合金元素的影响项,考虑其它合金元素对枝晶间液相流动的影响。解剖了6 t定向凝固钢锭,将宏观偏析预测结果与实测数据进行了比较。 图1 65 t钢锭中心线宏观偏析预测结果与实验结果比较Figure 1 The predicted results and experimental results of macro segregation along centerline of 65t steel ingot 图2 43 t钢锭中心线宏观偏析预测结果与实验结果比较Figure 2 The predicted results and experimental results of macro segregation along centerline of 43 t steel ingot 2010年,李殿中等人[17]采用连续模型预测了360 t钢锭的宏观偏析,并且考察了多包合浇工艺对宏观偏析预测结果的影响。 2010年,柳百成等人[18]采用连续模型对3.3 t钢锭凝固过程的热溶质对流和宏观偏析的形成进行了三维模拟,预测结果与实测吻合较好。2011年,考虑多包合浇工艺预测了300 t钢锭的宏观偏析[2]。 2011年,石伟等人[19、20]在Fluent软件平台上采用连续模型实现了22 t和600 t钢锭的凝固模拟,预测得到了明显的顶部正偏析和中心区域的通道偏析,并且研究了模型参数、合金成分以及工艺参数对宏观偏析预测结果的影响。 2003年,Appolaire和Combeau[21]建立了简化的一维多尺度模型,用于预测大型钢锭中心线上的宏观偏析。模型描述了等轴晶的形貌演变以及等轴晶在钢锭尺度上的宏观运动。采用Stokes公式计算单个等轴晶的沉降速度。预测了65 t钢锭中心线上的碳成分分布,并与实测进行了比较。此外,还考察了一个重要的模型参数——等轴晶沉降的流量密度对预测结果的影响。 2009年,Combeau等[8]采用两相模型预测了3.3 t钢锭的宏观偏析(二维模拟)。该钢锭是一个八角形钢锭,高2 m,平均直径0.6 m。研究了等轴晶的形貌和移动对钢锭宏观偏析形成的影响,将预测得到的钢锭纵剖面宏观偏析图谱和中心线宏观偏析曲线与实测进行了比较。Combeau等[22]进一步考虑等轴晶的形貌转变,应用两相模型预测了3.3 t钢锭的宏观偏析,并与实测进行了比较。值得注意的是,在Combeau等人[8、22]的研究中,形核模型采用的是瞬时形核模型,其中一个重要参数是初始形核密度N0。计算结果表明,在N0= 1010m-3条件下,该钢锭中的等轴晶发生了一个明显的形貌转变,此时预测的宏观偏析与实测吻合相对较好。 2010年,Combeau等人[23]采用两相模型预测了6.2 t钢锭的宏观偏析,比较了钢锭中心线和三个横轴上的预测结果和实验结果。研究表明,相比于等轴晶固定的情况,考虑等轴晶移动可以获得更好的预测结果。此外,针对模拟结果与实验结果之间存在的差距,Combeau等人[23]指出了模型改进的方向以及需要进一步开展的实验和理论研究。 2012年,本文作者建立了预测钢锭宏观偏析的两相模型。该模型考虑了合金凝固过程中宏观尺度上的传热、传质、液相对流和等轴晶移动以及微观尺度上的过冷、形核和晶粒生长。针对大型53 t试验钢锭进行了冒口解剖和成分分析,模拟并预测了钢锭凝固过程宏观偏析的形成,预测结果与试验结果较好吻合。结果表明,两相模型考虑了等轴晶的沉降,能够较好地描述大型钢锭底部负偏析区、顶部正偏析区和通道偏析的形成。 大型钢锭宏观偏析数值模拟是一个具有挑战性的课题。国内外的研究多采用比较简单的连续模型或体积平均模型。近年来,发展了考虑等轴晶移动的两相模型。从2009年开始,两相模型已经应用到3.3 t和6.2 t钢锭[8、23]中。最近,我们采用两相模型预测得到了大型钢锭(53 t)中的重要宏观偏析模式,特别是预测得到由等轴晶沉降所导致的钢锭底部“锥形”负偏析区域。然而,比较模拟结果与实验结果可知,目前的宏观偏析数学模型还有待进一步的改进和完善。此外,针对大型钢锭开展更加全面和细致的试验研究也很紧迫。 [1] 李文胜, 沈丙振, 周翔, 等. 大型钢锭凝固过程三维数值模拟. 大型铸锻件, 2010(3):1-4. [2] Liu B C, Xu Q Y, Jing T, et al. Advances in multi-scale modeling of solidification and casting processes. JOM, 2011, 63(4):19-25. [3] Beckermann C. Modelling of future needs macrosegregation: applications and future needs. International Materials Reviews, 2002, 47(5):243-261. [4] Lesoult G. Macrosegregation in steel strands and ingots: characterisation, formation and consequences. Materials Science and Engineering A, 2005, 413-414:19-29. [5] Bennon W D, Incropera F P. A continuum model for momentum, heat and species transport in binary solid liquid-phase change systems-I. model formulation. International Journal of Heat and Mass Transfer, 1987, 30(10):2161-2170. [6] Beckermann C, Viskanta R. Double-diffusive convection during dendritic solidification of a binary mixture. Physicochemical Hydrodynamics, 1988, 10(2):195-213. [7] Ni J, Beckermann C. A volume-averaged two-phase model for transport phenomena during solidification. Metallurgical Transactions B, 1991, 22(3):349-361. [8] Combeau H, Zaloznik M, Hans S, et al. Prediction of macrosegregation in steel ingots: influence of the motion and the morphology of equiaxed grains. Metallurgical and Materials Transactions B, 2009, 40(3):289-304. [9] Zaloznik M, Combeau H. An operator splitting scheme for coupling macroscopic transport and grain growth in a two-phase multiscale solidification model-part I: model and solution scheme. Computational Materials Science, 2010, 48(1):1-10. [10] Wu M, Ludwig A. Modeling equiaxed solidification with melt convection and grain sedimentation-I: model description. Acta Materialia, 2009, 57(19):5621-5631. [11] Wu M, Fjeld A, Ludwig A. Modelling mixed columnar-equiaxed solidification with melt convection and grain sedimentation-part I: model description. Computational Materials Science, 2010, 50(1):32-42. [12] Vannier I, Combeau H, Lesoult G. Numerical model for prediction of the final composition of heavy steel ingots // Chenot J L, Wood R D, Zienkiewicz O C. Proceedings of the 4th International Conference on Numerical Methods in Industrial Forming Processes. Rotterdam: Balkema, 1992:835-840. [13] Vannier I, Combeau H, Lesoult G. Numerical model for prediction of the final segregation pattern of bearing steel ingots. Materials Science and Engineering A, 1993, 173:317-321. [14] Gu J P, Beckermann C. Simulation of convection and macrosegregation in a large steel ingot. Metallurgical and Materials Transactions A, 1999, 30(5):1357-1366. [15] Gouttebroze S, Bellet M, Combeau H. 3D macrosegregation simulation with anisotropic remeshing. Comptes Rendus Mecanique, 2007, 335(5-6):269-279. [16] 顾江平. 定向凝固钢锭中宏观偏析的数值模拟及控制[博士学位论文]. 北京: 清华大学机械工程系, 1995. [17] Liu D R, Sang B G, Kang X H, et al. Numerical simulation of macrosegregation in large multiconcentration poured steel ingot. International Journal of Cast Metals Research, 2010, 23(6):354-363. [18] Li W S, Shen H F, Liu B C. Three-dimensional simulation of thermosolutal convection and macrosegregation in steel ingots. Steel Research International, 2010, 81(11):994-1000. [19] Wang L, Shi W. Numerical simulation of macrosegregation during steel ingot solidification using continuum model. Journal of Shanghai Jiaotong University (Science), 2011, 16(2):145-148. [20] 王励. 大型钢锭凝固模拟与成分偏析预测[硕士学位论文].北京:清华大学机械工程系, 2011. [21] Appolaire B, Combeau H. Modelling of the settling of equiaxed crystals during the solidification of large steel ingots // Stefanescu D M, Warren J, Jolly M, et al. Modeling of Casting, Welding and Advanced Solidification Processes X. Warrendale, PA: TMS, 2003:221-228. [22] Combeau H, Kumar A, Zaloznik M. Modeling of equiaxed grain evolution and macrosegregations development in steel ingots. Transactions of the Indian Institute of Metals, 2009, 62(4-5):285-290. [23] Kumar A, Zaloznik M, Combeau H. Prediction of equiaxed grain structure and macrosegregation in an industrial steel ingot: comparison with experiment. International Journal of Advances in Engineering Sciences and Applied Mathematics, 2010, 2(4):140-148. [24] Li W S, Shen B Z, Shen H F, et al. Modelling of macrosegregation in steel ingots: benchmark validation and industrial application. IOP Conf. Series: Materials Science and Engineering, 2012, 33:012090. [25] 李文胜. 基于两相模型的大型钢锭宏观偏析数值模拟[博士学位论文]. 北京: 清华大学机械工程系, 2012.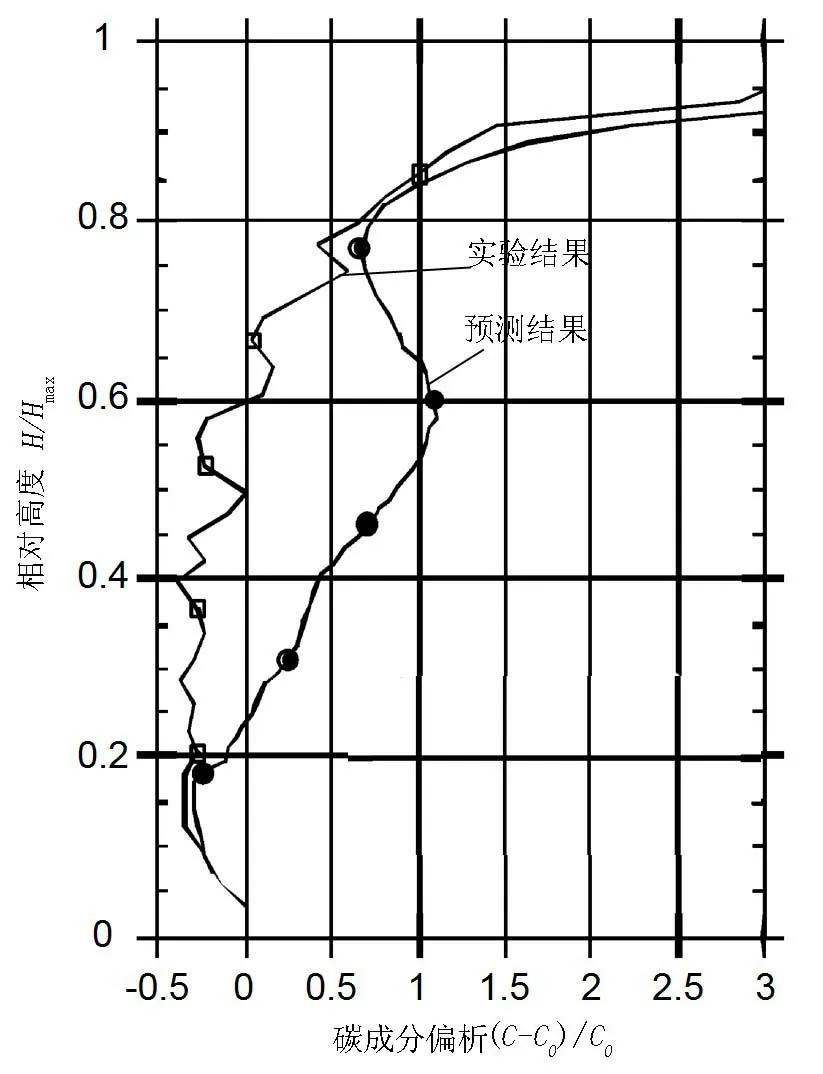
2.2 两相/多尺度模型
3 结语

