小波变换在电能质量扰动检测中的探讨

魏 茹，栾鹏飞

（鄂尔多斯电业局，内蒙古 鄂尔多斯017000）

0 引 言

现代社会中，电能已成为一种广泛使用的能源，其应用程度成为一个国家发展水平的主要标志之一。电能是一种经济、实用、清洁且容易控制和转换的能源形态，又是电力部门向用电用户提供由发、供、用共同保证质量的一种特殊产品。随着国民经济和科学技术的发展，对电能的需求量日益增加，同时对电能质量的要求也越来越高［1，2］。

由于暂态电能质量信号是非平稳信号，这正适用于小波变换的方法。将小波变换用于暂态电能质量分析领域，将具有FFT、STFT所无法比拟的优点。目前小波分析方法在很多领域得到了广泛应用，尤其是小波变换在暂态电能质量分析领域中的成功应用。利用小波变换在信号突变点的特性，可以实现电能质量扰动信号起止时刻的检测。

1 小波变换方法

小波就是最短最简单的振动，它是由Morlet于1980年在进行地震数据分析工作时创造的。小波分析方法是一种窗口大小（即窗口面积）固定但其形状可改变的时域局部化分析方法，它在高频部分具有较高的时间分辨率和较低的频率分辨率，而在低频部分具有较高的频率分辨率和较低的时间分辨率，所以被誉为“数学显微镜”。正是这种特性，小波变换具有对信号的自适应性［3，4］。小波变换由于具有时域局部化的特点，克服了以往FFT和STFT的缺点，特别适合于非平稳信号和突变信号的分析。

根据小波变换在信号突变点的特点，在小波变换局部模极大值理论的基础上，通过二进小波变换对电能质量扰动信号进行分析，可以在时域实现比较准确的检测。

2 小波变换的奇异性检测理论［5，6］

信号突变点检测是小波变换应用的一个很重要的方面。信号突变点在小波变换域常对应于小波变换系数模的极值点或过零点，并且信号奇异性的大小同小波变换系数的极值随尺度的变化规律相互对应。因此，将小波变换应用于对信号的瞬态特征描述是极其有意义的。目前，小波变换已在该领域获得了广泛的应用。

说明：本文中的小波变换的定义不是传统所用的内积形式：

而是卷积形式：

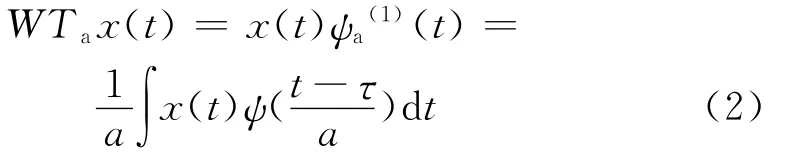
这也就是把小波变换WTax（t）看成是信号x（t）通过激励响应为ψa（1）（t）的系统后的输出。两种定义方式当ψ（t）和ψ（1）（t）都是实函数时，如果ψ（1）（t）＝ψ（－t），则有

如非对称，在计算方法上也没有本质区别。

一般取尺度因子a＝2J，J∈Z，而t取连续变化的值，简称J为尺度。则上述小波变换被称为卷积型二进小波变换。二进小波变换是稳定的、完备的，而且具有平移不变性，因此二进小波变换经常用于信号的奇异性检测当中。

多尺度边缘检测则是采用平滑函数对信号的不同尺度下进行平滑，然后从一阶导数或二阶导数检测其奇异点。多尺度边缘检测和小波变换检测从思想方法上是一致的，以下直接从小波变换出发讨论信号奇异性的多尺度检测。

若θ（t）是某一起平滑作用的低通平滑函数，且满足以下条件：

为方便起见，不妨取θ（t）为高斯函数，即

假定平滑函数θ（t）二次可导，并定义ψ（1）（t）、ψ（2）（t）分别是θ（t）一阶、二阶导数：

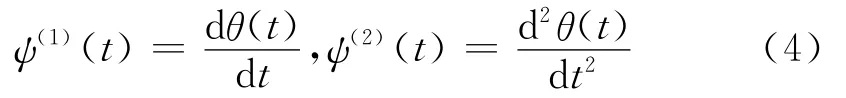
则函数ψ（1）（t）、ψ（2）（t）满足小波的可容许性条件：

因此ψ（1）（t）、ψ（2）（t）可作为小波母函数。

若对任意函数g（t），引进记号

则ga（t）表示函数g（t）在尺度因子a的伸缩，由于小波变换就是通过将原信号f（t）同伸缩小波卷积得到的，以ψ（1）（t）为小波函数，函数f（t）在尺度因子a位置为t处的卷积型小波变换定义为：

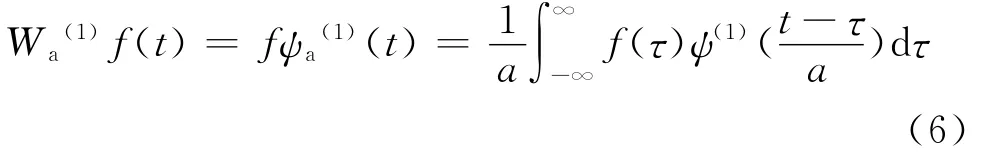
对应于ψ（2）（t）的小波变换为：

据此可以导出

由于fθa（t）可以看成是由低通平滑函数θ（t）在尺度因子a下对函数f（t）进行平滑的结果，由式（8）、（9）得知，小波 变换f（t）和f（t）可 分 别 理解为函数f（t）在尺度因子a下经平滑后的一阶、二阶导数。由上可知，当小波函数可看作某一平滑函数的一阶导数时，信号的突变点（或边缘点）与信号小波模的局部极值点相对应。当小波函数可看作是某一平滑函数的二阶导数时，信号小波变换模的过零点，也对应于信号的突变点（或边缘点）。

因此，采用检测小波变换局部极值点和系数模的过零点的方法可检测信号的突变点，这是两种相似的方法。但是比较来说，用局部极值点进行检测更具有优越性，由于函数fθa（t）的拐点既对应于它的一阶导数模的极大值点，又对应于极小值点。极小值点（t1）对应于缓慢变化的点，而｜Wa（1）f（t）｜极大值点（t0，t2）是对应于信号尖锐变化的点，所以单凭检测二阶导数的过零点很难区分是信号的突变点还是缓慢点。因此，在信号奇异性检测中，使用更多的是极大值检测。

综上所述，利用平滑函数一点导数构造的小波，其小波变换信号的尖锐变化点与模极大值将相对应，检测其模极大值也就相当于检测出了信号的奇异点，其小波变换在各尺度系数下的极大值对应于信号的突变点位置。只有在适当尺度下各突变点引起的小波变换才能避免交叠干扰，因此，在处理时应该把多尺度结合起来综合观察。

3 多孔算法［6，7，8］

离散信号的二进小波变换可以通过多孔算法来实现，它适用于a＝2J二分树结构。它的计算过程是把冲激响应h0，h1序列（h0，h1为 Mallat算法中的滤波器组）的各点间插入适当零值再做卷积而得，将离散信号作为c0，计算过程如下：

hJ为h的相邻两项之间插入2J－1个零值。这样就可以将离散信号各个采样点的小波变换全部计算出来。

4 结束语

电能质量扰动持续时间、起止时刻是描述扰动的重要属性，对电能质量扰动进行有效地检测，有助于电能质量综合评估，对于电能质量的综合治理和提高具有重要意义。本文基于小波变换局部模极大值理论，采用二进小波变换对电能质量扰动进行检测，其在分解尺度上可以实现较为准确的检测。

［1］ 林海雪.现代电能质量的基本问题［J］.电网技术，2001，25（10）：5－12.

［2］ 肖湘宁，徐永海.电能质量问题剖析［J］.电网技术，2001，25（3）：66－69.

［3］ 胡 铭，陈 珩.电能质量极其分析方法综述［J］.电网技术，2000，24（2）：36－38.

［4］ 张 斌，刘晓川，许之晗.基于变换的电能质量分析方法，电网技术［J］.2001，25（1）：26－29.

［5］ 彭玉华.小波变换与工程应用［M］.北京：科学出版社，1999.

［6］ 杨福生.小波变换的工程分析与应用［M］.北京：科学出版社，1999.

［7］ Mack J Shensa.The Discrete Wavelet Transfor m：Wedding the A Trous and Mallat Algorithms［J］.IEEE Transactions on Signal Processing，1992，40（10）：2464－2482.

［8］ Olivier Rioul，Pierre Duhamel.Fast Algorith ms for Discrete and continuous Wavelet transf or ms［J］.IEEE Transactions on Inf or mation Theory ，1992，38（2）：569－586.