考虑空间相关性的居民居住选址模型
杨励雅,邵春福
(1.中国人民大学公共管理学院,北京100872;2.北京交通大学交通运输学院,北京100044)
居民居住选址直接影响城市居住空间结构的形成与演进,且在很大程度上决定城市通勤交通模式,还与住房制度改革、房地产市场等制度经济因素具有深刻的联系,因此一直是交通、地理、房地产等领域的研究热点[1-5]。
空间相关性是研究居民居住选址时应考虑的关键因素。正如Tobler[6]提出的“地理学第一定律”中所述“空间上分布的事物是相互关联的,且距离近的事物之间的相关性大于距离较远的事物之间的相关性”。目前国内外有关居民居住选址建模的研究中[1-5,7],对备选方案之间空间相关性的考虑不足,这主要是计算模型的限制所致。
基于随机效用最大化的离散选择模型是居民居住选址研究中最常用的分析方法。其中,多项Logit模型应用最为广泛,例如Gabriel[1]和Guo[2]构建了居民居住选址的MNL模型,并利用模型计算结果进行了预测分析。但由于MNL模型具有IIA性质,即假设备选方案之间是相互独立的,因此将MNL模型应用于空间方案选择中可能会导致预测的失误[8-9]。随后出现的巢式Logit模型允许每个“巢”内的备选方案之间具有相关性,能在一定程度上克服MNL模型的IIA性质。Hunt[3]、Boots[4]、Deng[5]、Abraham[7]等利用NL模型研究了居民居住地选择及其他空间选择问题。NL模型尽管考虑了空间相关性,但在建模时要求研究者事先确定“巢”以及每个“巢”内备选方案的个数,即备选方案集合被人为地划分为多个相互独立的子集合,主观性较大[10]。
广义极值模型GEV的出现,是离散选择模型发展进程中的重大突破,其结构灵活多样,可以捕捉任意备选方案之间的关联性,同时具有封闭形式的概率表达式,无需借助模拟技术就可以被估计出来[8]。
本研究利用GEV模型的理论基础,构造空间相关背景下居民居住选址的配对巢式Logit模型,并利用模型对重庆市主城区居民居住选址进行参数估计、检验及直接弹性与交叉弹性分析。
1 基于GEV的配对巢式Logit模型
GEV模型允许各备选方案的随机效用项之间存在相关性,根据各备选方案之间关联结构的不同,可形成不同形式的GEV模型,因此通常被称作“GEV家族”[9],MNL及NL模型是GEV模型的基本类型。本研究在Bhat[9]和Koppelman[11]研究的基础上,构建考虑空间相关性的居民居住选址的配对巢式Logit模型。
1.1 模型结构
一般而言,相邻备选空间因交通区位、基础设施、经济水平等因素较为接近,因此存在较强的相关性,而非相邻空间的各类属性因素差异较大,相关性不显著。本研究假定相邻备选空间具有相关性,而非相邻空间之间相互独立,将相邻的备选方案两两组合构成一个个的“巢”,形成一种特殊的配对巢式结构。假定I为备选方案的个数(i=1,2,…,I),令ωij为0-1变量,取1表示备选空间i和j相邻,取0则表示不相邻,模型中“巢”的个数为。为便于说明,假设备选方案集合由4个空间单元组成,如图1(a)所示,其模型结构如图1(b)所示。
1.2 选择概率的推导
根据GEV模型理论,备选方案的选择概率可由以下G函数[9]推导:
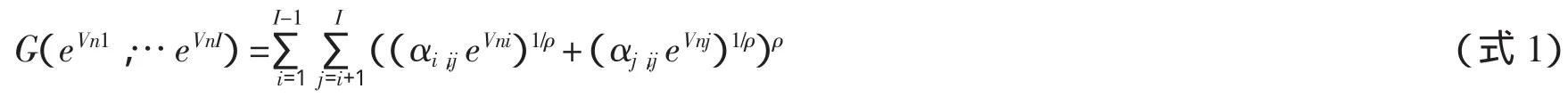
式 1 中,I为备选方案(空间)的个数,i=1,2,…I;αi,ij为分配参数,即备选方案 i对“i-j配对”的隶属度,0< αi,ij<1,,且;Vni为备选方案i对个人n的效用的确定项;ρ为异质参数,0<ρ≤1。

图1 包含4个居住备选方案的配对巢式Logit模型结构示例Fig.1 A simple example of residential choice among four spatial units
为表述方便,后文所有表示效用及概率的符号下标中均省略代表选择者的“n”。式1中,异质参数ρ越接近0,则各备选方案之间的相关性越大,而当ρ=1时,各方案之间保持独立,式1退化为MNL模型的G函数[9]。
假定每个备选方案的效用误差项εi均服从标准Gumbel分布,则I个备选方案的联合累积分布函数为:
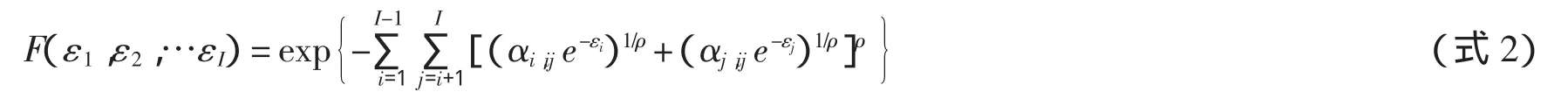
根据GEV模型性质,可推导出第个备选方案的选择概率:
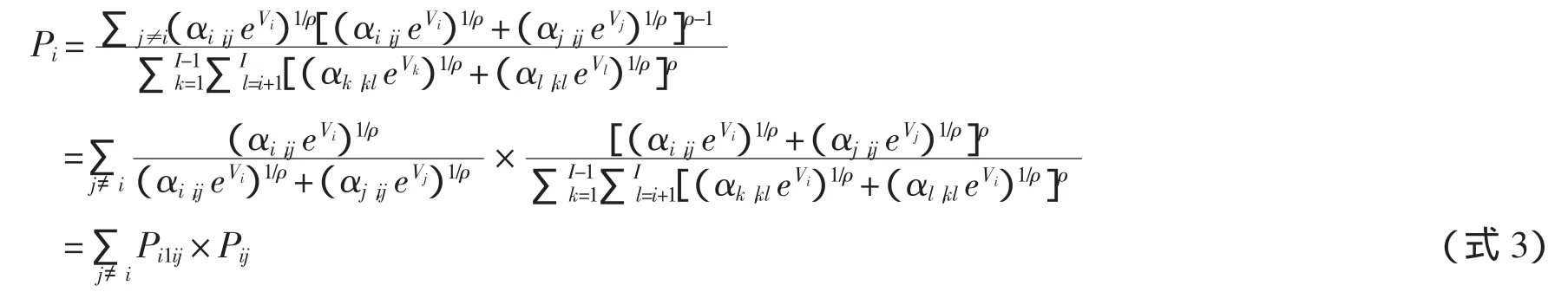
式3中,Pi1ij为备选方案i在“i-j配对”中的选择概率;Pij为“i-j配对”被选择的概率。式3中的未知参数包括异质参数ρ以及效用函数确定项Vi中各变量的系数。
1.3 直接与交叉弹性分析
通过直接与交叉弹性分析,可进一步反映配对巢式Logit模型与传统MNL模型的区别。直接弹性被定义为备选方案i的第k个效用变量值变化1%时,方案i选择概率发生的变化;间接弹性则指备选方案i的第k个效用变量值变化1%时,方案j选择概率发生的变化。这里,假设备选方案效用函数的确定项是一个线性函数,即:

式4中,K为备选方案i的系统效用Vi所包含的变量个数;xik为系统效用Vi的第k个变量;βk为第k个变量所对应的未知参数。
根据Wen等[12]的研究,可推导出直接弹性与交叉弹性的表达式,如表1所示。

表1 MNL与配对巢式Logit模型的直接与交叉弹性公式对比Tab.1 Expressions for the direct and cross elasticity in the MNL and Paired Nested Logitmodels
可以看出,MNL模型交叉弹性表达式中未包含下标j,即方案i的效用变化对任何方案j的影响均相同,这是由MNL模型的IIA特性决定的。在配对巢式Logit模型中,当i和j不相邻时(此时i和j之间无空间相关性)交叉弹性表达式与MNL模型相同,而当i和j相邻时,交叉弹性高于MNL模型且其值受方案j选择概率的影响,即方案i的效用变化对不同方案j的影响是不同的,这说明配对巢式Logit模型考虑了相邻备选方案之间的相关性。
2 模型应用
2.1 数据来源
本文数据主要来源于2008年重庆市主城区综合交通调查,并以外环高速所环绕的主城核心区为研究对象。涉及行政区域有渝中区、南岸区、沙坪坝区、江北区、九龙坡区、大渡口区和北碚区,包含交通小区(TAZ)39个。住房数据主要来源于重庆市房地产交易管理网①重庆市房地产网www.cqfdckf.com,2008-08;重点城市房地产市场月报数据和监测报告上报系统http://219.142.101.174/mrwebnew/default.aspx,2008-12。。
2.2 效用变量选取
Alonso[13]和Mills[14]在建立经典空间结构解析模型时指出,居民的居住区位选择是在预算约束下对住房成本和通勤成本进行权衡,追求效用最大化。考虑数据的限制,本研究选取小区住房成本、小区通勤成本、小区主要公用设施个数作为小区特征变量;选取与小区所有家庭年平均收入之差、与小区所有家庭平均人均住房面积之差作为家庭的社会经济属性变量。模型的所有变量说明如表2所示。因本研究以交通小区(TAZ)作为基本分析单元,所以住房成本和通勤成本等都在区块层面进行平均,作为该区块的特征值。其中,通勤成本的计算方法如下。
通勤成本是指居住在某一交通小区的就业者从居住地到就业地的平均通勤成本[15]。居住在小区的典型就业者在小区j就业的概率θij可由式表示:

式5中,Aij为早高峰时期从小区i到小区j的通勤出行量,反映居住在小区i的就业者在小区j就业的数量,可由居民出行调查获得。则小区i的典型就业者的通勤成本Ti为:

式6中,cij为居住在小区的就业者到小区j通勤的广义费用,本研究用出行距离代替。
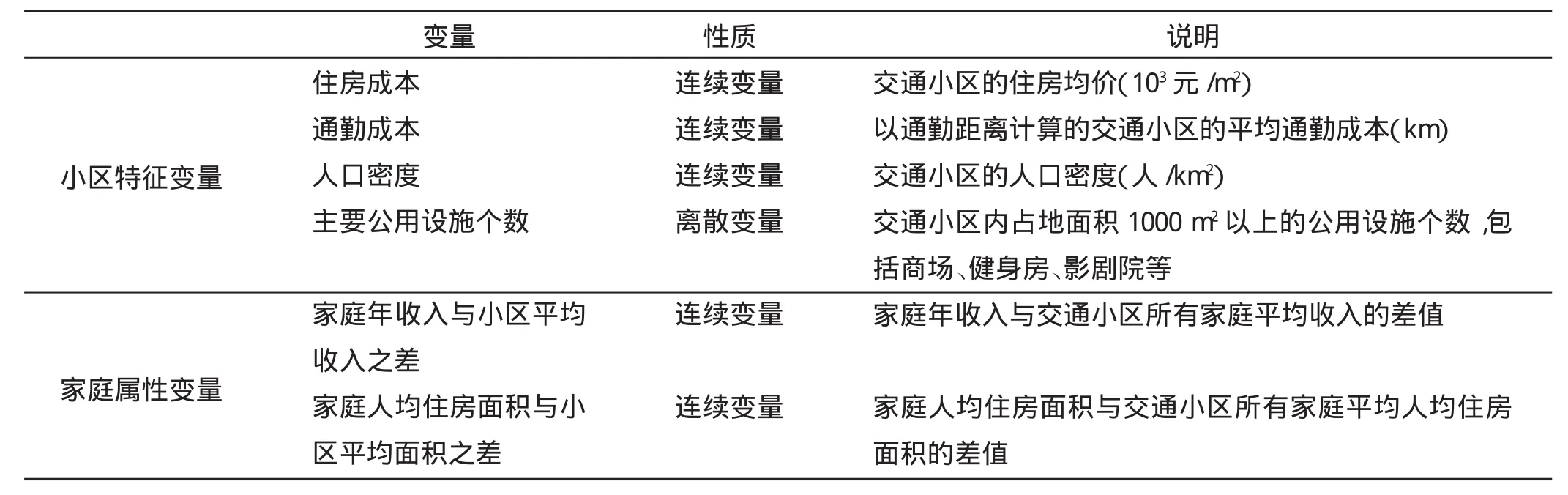
表2 模型的变量说明Tab.2 Model variables specification
2.3 参数估计
根据上述变量数据,构建重庆市主城区居民居住选址的配对巢式Logit模型。需要估计的模型参数包括异质参数ρ和各效用变量系数βk。为将配对巢式Logit模型与传统MNL作对比,同时构建重庆市居民居住选址的MNL模型。参数估计方法为极大似然法,采用Biogeme软件包进行参数估计,计算结果如表3所示。从表3中两个模型的拟合优度与似然比可以看出,配对巢式Logit模型具有更为优越的统计学特征。二者关于模型变量的参数估计值基本接近。其中,通勤成本、住房成本的参数值为负,且通勤成本参数值的绝对值大于住房成本,表明相较住房成本,通勤成本在居民居住选址决策中所起的作用更大。反映家庭社会经济属性的家庭年收入与小区平均收入之差、家庭人均住房面积与小区平均人均住房面积之差对居民居住选择的影响不显著。产生这一现象的原因可能在于研究时点(2008年)重庆市房地产市场发育尚不完善,房地产产品供给市场的细分化不明显;另一方面住房货币化制度实施时间较短,消费者的个人社会经济属性差异在购房选择中的作用尚未得以体现。异质参数ρ为0.385<1,且显著性较高,表明相邻备选方案之间具有较高的相关性。
2.4 直接与交叉弹性分析
本研究选择3个小区进行分析,一个为任选的某一家庭所在小区,其他两个一个与该小区相邻,一个不相邻。根据表1的计算公式,可得到配对巢式Logit模型以及传统MNL模型的直接与交叉弹性,如表4和表5所示。
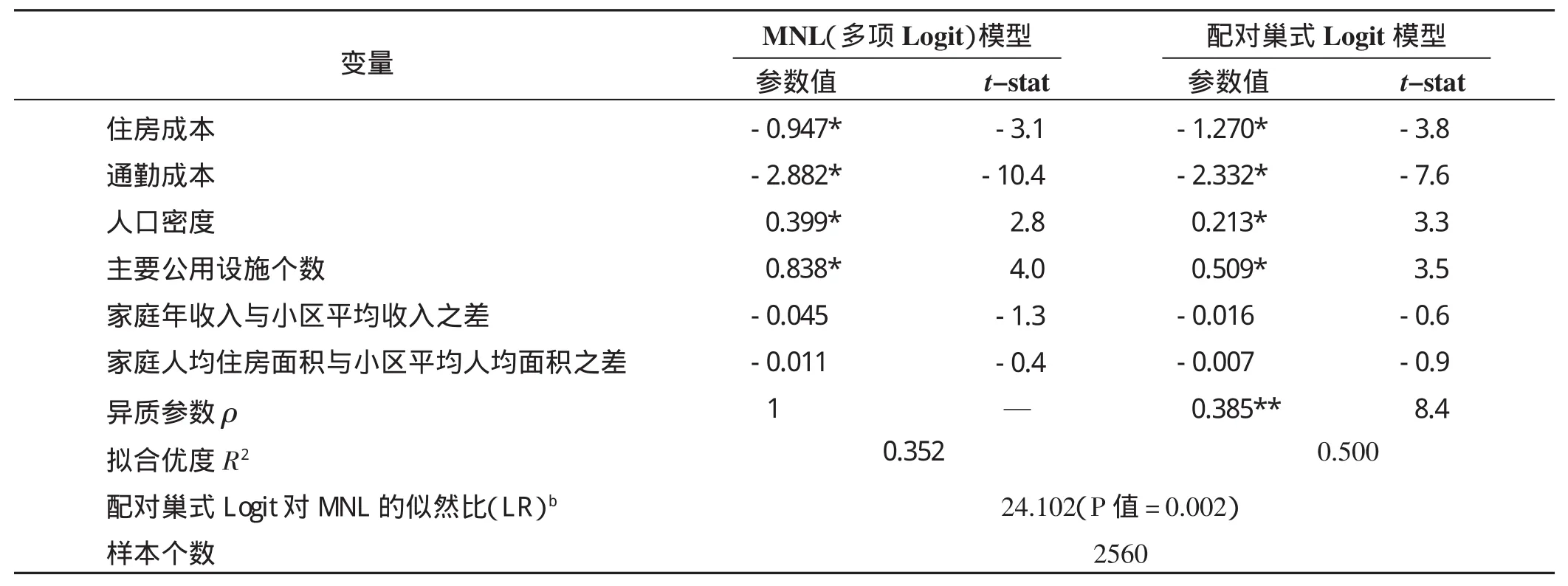
表3 配对巢式Logit模型与MNL模型的参数估计结果Tab.3 Estimation results of MNL and Paired Nested Logit models

表4 MNL模型中各效用变量的直接与交叉弹性Tab.4 Direct and cross elasticity of every utility variable in MNL model

表5 配对巢式Logit模型中各效用变量的直接与交叉弹性Tab.5 Direct and cross elasticity of every utility variable in Paired nested model
弹性分析进一步反映了两种模型的区别。MNL模型中,事先选定的家庭所在小区的效用变量对所有其他小区的交叉弹性均相同。配对巢式Logit模型考虑了相邻备选方案之间的空间相关性,故事先选定的家庭所在小区效用变量对不与其相邻小区的交叉弹性值保持一致,而对与其相邻小区的交叉弹性值各不相同。
3 结论
本研究的主要研究成果在于:(1)提出一种基于GEV理论的配对巢式Logit模型,能刻画相邻备选方案的空间相关性,具有更优的统计学特征,使得精确预测居民居住选址行为成为可能,进而可以保证相关交通、土地开发政策更具针对性。(2)分别对配对巢式Logti模型和MNL模型进行效用变量的弹性分析,进一步反映出两种模型的区别。在MNL模型中,某备选方案效用变量的改变对其他所有方案选择概率的影响相同,而在配对巢式Logit模型中,某备选方案效用变量的改变对其他方案选择概率的影响不同,且对其相邻方案的影响大于对其不相邻方案的影响。(3)对重庆市主城区的实证研究表明,通勤成本与住房成本是影响居民居住选址的两大重要因素,且通勤成本的影响大于住房成本,而家庭的社会经济属性对居民居住选址行为影响不明显。
(
):
[1]Gabriel,S.A.,Rosenthal,S.S.Household location and race:estimates of a multinomial logit model[J].The Review of Economics and Statistics,1989,17(2):240-249.
[2] Guo,J.Y.,Bhat,C.R.Residential location choice modeling:a multinomial logit approach[J].Technical paper,Department of Civil Engineering,University of Texas at Austin,2001.
[3] Hunt,L.M.,Boots,B.,Kanaroglou,P.S.Spatial choice modeling:new opportunities to incorporate space into substitution patterns[J].Progress in Human Geography,2002,28(6):746-766.
[4] Boots,B.N.,Kanaroglou,P.S.Incorporating the effect of spatial structure in discrete choices models of migration[J].Journal of Regional Science,1988,28(4):495-507.
[5] Deng,Y.,Ross,S.L.,Wachter,S.M.Racial differences in homeownership:the effect of residential location[J].Regional Science and Urban Economics,2003,33(5):517-556.
[6] Tobler,W.A computer model simulating urban growth in the Detroit region[J].Economic Geography,1970,46(2):234-240.
[7] Abraham J.E.,Hunt J.D.Specification and estimation of a nested logit model of home,workplace and commuter mode choice by multiple worker households[J].Transportation Research Part B,2007,41(7):795-808.
[8]Koppelman,F.S.,Sethi,V.Closed-form discrete choice models[M].In:Hensher,D.A.,Button,K.J.(Eds),Handbook of transport Modeling,second ed.Elsevier Science,2008:211-225.
[9] Bhat,C.R.,Guo,J.Y.A mixed spatially correlated logit model:formulation and application to residential choice modeling[J].Transportation Research Part B,2004,38(2):147-168.
[10] Bekhor,S.,Prashker,J.N.GEV-based destination choice models that account for unobserved similarities among alternatives[J].Transportation Research Part B,2008,42(3):243-262.
[11]Koppelman,F.S.,Wen,C.H.The paired combinatorial logit model:properties,estimation and application[J].Transportation Research Part B,2000,34(2):75-89.
[12]Wen,C.H.,Koppelman,F.S.The generalized nested logit model[J].Transportation research Part B,2001,35(7):627-641.
[13]AlonsoW.Location and land use[M].Cambrideg:Harvard University Press,1964.
[14] Mills E.S.An aggregative model of resource allocation in a metropolitan area[J].American Economic Review,1967,57:197-210.
[15]郑思齐,刘可婧,孙伟增.住房与交通综合可支付性指数的设计与应用——以北京为例[J].城市发展研究,2011,18(2):55-61.

