混合改进蚁群算法的函数优化

陈明杰，黄佰川，张旻

(哈尔滨工程大学自动化学院，黑龙江哈尔滨150001)

自2000年国际顶级学术刊物《Nature》发表了M.Dorigo的蚁群算法综述以来，模拟自然界蚂蚁进行最优路径搜索的蚁群算法 (ant colony optimization，ACO)［1-13］作为求解组合优化问题的有效手段，逐渐成为智能优化算法领域的热点［1］.由于其算法上具有正反馈机制、分布式计算、贪婪式搜索特征以及鲁棒性强、并行处理等特点［2］，目前已被广泛应用于组合优化问题中，在车辆调度问题、机器人路径规划问题等领域均取得了良好的效果.对一般函数的优化问题也表现出优异的性能，它可以克服传统优化方法的许多不足和缺陷，实现简单，在函数不连续、不可微、局部极值点密集等苛刻的情况，仍然具有很好的寻优能力［3］.W.J.Gutjahr发表的证明蚁群算法收敛性的文章在蚁群算法的发展过程中具有重要的意义［10］.但是，到目前为止，蚁群算法仍然存在很多不足，如易出现停滞现象、搜索时间长和解空间搜索不够等缺点［4］.针对蚁群算法存在的上述问题，本文在文献［5］的基础上加以改进，提出了一种混合改进蚁群算法，并将其应用于函数优化问题中.

1 基于蚁群算法的函数优化原理

文献［5］所提出的基于蚁群算法的函数优化原理如下.

不失一般性，在函数的优化问题中，所有的优化问题都可以表示为一个函数的最小化问题，即:

式中:c为常数.如果在函数优化中存在端点值，那么可以先将端点值剔除，最后计算比较.在下面的算法中将不再考虑端点值.

在多元函数优化问题中，设决策变量由n个分量组成，并要求决策变量的每一个分量都精确到小数点后d位，则可构造一副由n×d+n+1层数字组成，且第1、d+2、2d+3，…层由一个标号为0的数字组成，其余层都由标号为0～9的10个数字组成，第(b－1)×(d+1)+2到 b×(d+1)层(b=1，2，…，n)表示决策变量的第b个分量，其余层都是辅助层.解码时，对各分量对应的层分别解码.采用这种方法，每个决策变量分量的最后一位与下一个分量的第一位之间都有辅助层隔开，因此前一个分量的末位不会影响后面一个分量的首位.

将待优化函数的决策变量表示为一串十进制的数字串{d(0)，d(1)，…，d(l－1)}，而决策变量可以通过解码公式(2)解码得到［6］:

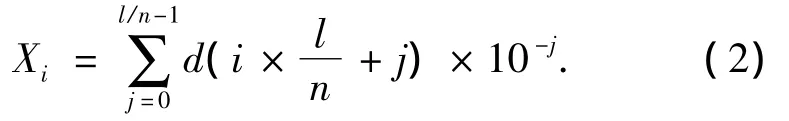
式中:l为决策变量字符串的长度，n为决策变量的维数.式(2)所代表的解码过程可以用图1来描述.

图1 蚂蚁路径选择Fig.1 Chosen path of ants

假设l=8，n=2，那么图1所示的路径由式(2)解码后得到的决策变量为X=(X1，X2)=(0.206 4，0.971 3).

在图1所示的蚂蚁路径选择中，可知在蚂蚁路径的终点和起点之间有很多层数字.蚂蚁要想从起点走到终点就必须经过每层数字，这样蚂蚁在每经过一层数字时，将会从10个数字中做出选择，蚂蚁在经过下层数字时从哪个节点经过根据式(3)选择:

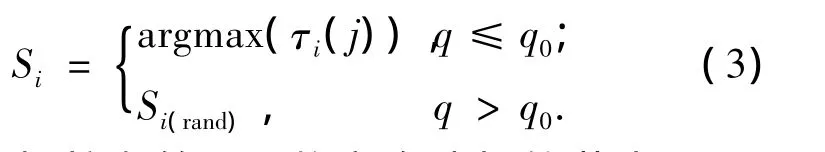
式中:Si为蚂蚁在第i层数字会选择的节点号码;argmax为第i数字层上使得τi(j)最大的节点j的值;τi(j)是第i层数字上第j个节点上的信息素残留量，q是一个随机数，且 q∈［0，1］，q0是信息素阈值，q0∈［0，1］，根据经验一般设为0.8;Si(rand)为第 i层数字中j号节点被蚂蚁选中的概率，由式(4)计算得出:

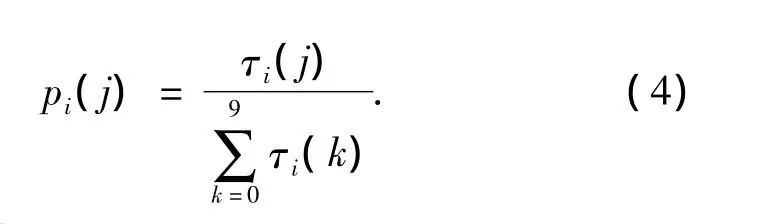
式中:pi(j)为第i层数字中节点j被蚂蚁选择的概率.

蚂蚁每经过一层数字中的某个节点时，都会根据局部信息素残留更新式(5)，修改该节点上的信息素残留量.

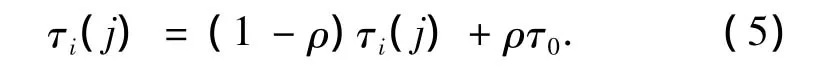
式中:τ0是常数，表示初始时刻信息素的含量;ρ是数字节点上的信息素挥发速度，ρ∈［0，1］.

当蚂蚁如图1所示在每层数字中选择好一个节点后，这时蚂蚁就找到了一条路径.将这条路径按式(2)解码可以获得决策变量的值，这样就可以求得函数值.当蚁群中每只蚂蚁都按照图1找到一条路径后，就可以在蚁群中找到一只蚂蚁，它走过的路径解码后得到的决策变量使函数值最小，称这只蚂蚁为迭代最优蚂蚁.让迭代最优蚂蚁的函数值和全局蚂蚁的函数值相比较，如果迭代最优蚂蚁路径解码后求出的函数值要小于全局最优蚂蚁解码后求出的函数值，那么迭代最优蚂蚁成为全局最优蚂蚁.当蚁群中每只蚂蚁都选择好路径后，这时全局最优蚂蚁要根据信息素残留量的全局更新式(6)对所经过的第i层数字的第j个节点上的信息素残留量τi(j)进行更新:

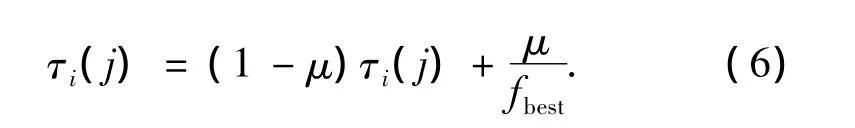
式中:τi(j)为最优蚂蚁在第i层数字中所选择的节点j上的信息素残留量;μ是一个常数，且μ∈［0，1］;fbest表示全局最优蚂蚁解码后求出的函数值.

该蚁群算法就是一直重复进行上述蚂蚁选择的路径和信息素更新的过程，至满足结束条件.

文献［5］所提到的蚁群优化算法采用十进制编码，缩短了蚂蚁需要搜索的路径长度;信息素直接存储在数字层的数字上面，减少了信息素的存储量;采用了信息素局部更新和全局更新相结合的信息素更新规则.但上文所提到的蚁群优化算法仍然有不足:1)容易陷入局部最优，算法的全局搜索能力有待提高;2)在处理维数较多的函数问题时，搜索速度有待提高.

2 混合改进蚁群算法的原理

本文在文献［5］的基础上研究了一种基于自适应信息素挥发因子、决策变量高斯变异和决策变量边界自调整3种改进策略的混合改进蚁群算法，提高基本蚁群算法的收敛速度和全局搜索能力.

2.1 基于自适应信息素挥发因子的蚁群算法改进

研究发现，蚁群算法是启发式算法和信息素正反馈机制相结合产生的算法.在蚁群算法搜索最优解过程中，应用的是随机选择策略，而随机策略会使蚁群算法的进化速度较慢;蚁群算法中的信息素正反馈机制的目的在于强化蚂蚁搜索到的较优的解，但很容易出现停滞现象［7］.这正是蚁群算法的不足之处.

为了克服上述不足，在蚁群算法的寻优过程中，当迭代一定次数、进化方向基本确定时，利用自适应改变信息素挥发因子大小的方法，对寻优路径上的信息素作动态调节，逐渐缩小最优路径和最差路径上的信息量，以实现对决策变量空间的充分寻优.

本文引入一种自适应信息素挥发因子，探讨了一种基于自适应信息素挥发因子的蚁群算法的改进.该方法旨在使产生的新的蚁群算法通过信息素挥发因子μ的自适应来提高算法的全局性.即将式(6)中的全局信息素挥发因子μ用随迭代自适应的μ(t)代替，此时式(6)变为

式中:μ(t)是随迭代变化的信息素挥发因子，μ(t)按式(8)进行自适应变化:

式中:μmin表示 μ的最小值，其目的是可以防止由于μ过小使算法的收敛速度变慢.为了提高算法的全局搜索能力，提高算法的搜索速度，在每次循环搜索结束时，都求出最优解，并将最优解保留，作为判断μ自适应的条件.

2.2 基于决策变量高斯变异的蚁群算法改进

在蚁群算法的搜索寻优过程中，当优化函数的非全局极值点比较集中时，会影响算法的收敛速度，并可能陷入局部最优，得不到高精度的解.为了使搜索到的解有更好的遍历性，收敛速度更快，摆脱局部最优，本文加入决策变量高斯变异策略，将待优化函数的决策变量进行高斯变异，提出了一种基于决策变量高斯变异的蚁群改进算法.以加强解的多样性，扩大搜索范围，使算法在搜索过程中加快搜索速度，摆脱局部最优.

基于决策变量高斯变异的蚁群算法改进原理如下［8］.

高斯分布式概率论是数理统计中一类重要的分布.将高斯变异应用到蚁群算法，其思想主要来自于遗传算法中的变异因子.在蚁群算法中应用高斯变异来改善蚁群算法的全局搜索能力，避免早熟，并加快收敛速度.式(9)是以原点为中心的高斯函数(Gaussian)，其概率分布如图2所示.

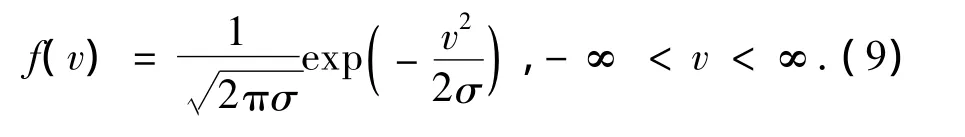
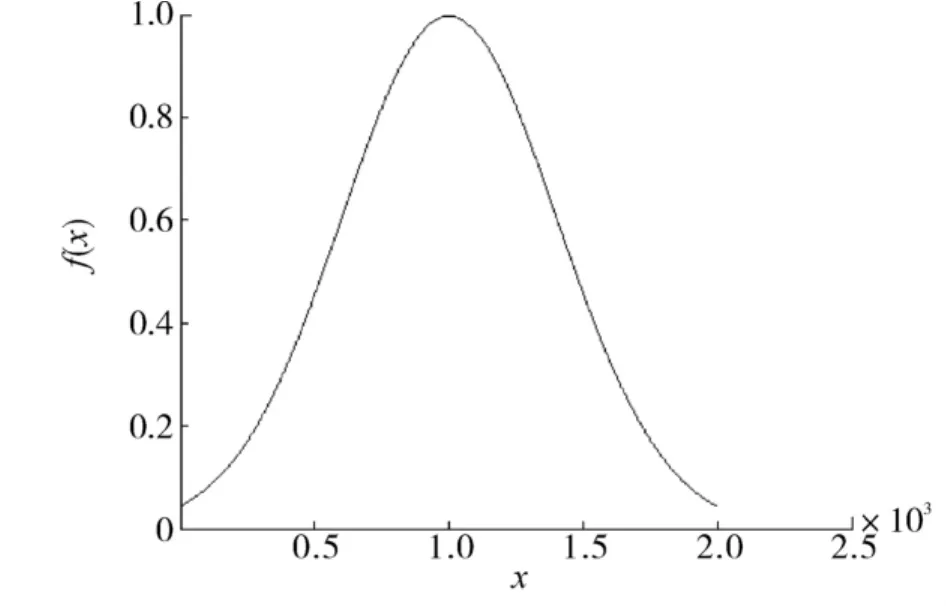
图2 高斯分布概率分布Fig.2 Gaussian distribution

在式(1)所示的函数优化问题中，函数的决策变量用X表示，决策变量的维数为n;lb表示决策变量的下界，每一维决策变量的下界用lb(i)表示;ub表示决策变量的上界，每一维决策变量的上界用ub(i)表示;设MX表示经高斯变异后的决策变量，MX(i)表示变换后的第i维决策变量;为了使高斯分布覆盖整个决策变量空间，设Gaussian分布函数中的参数σ =0.16.

决策变量高斯变异基本步骤如下:

1)给经高斯变异后的决策变量赋初值;

2)求出决策变量上下界的均值和均方差;

3)根据Gaussian分布函数产生一个均值为2)求出的决策变量上下界的均值，均方差为2)求出的决策变量上下界的均方差的随机数;

4)将3)产生的随机数限定在决策变量的上下界之间;

5)将4)产生的随机数作为高斯变异后的决策变量.

2.3 基于决策变量边界自调整的蚁群算法改进

在蚁群算法的寻优过程中，特别是在高维的函数寻优中，由于蚁群的寻优范围较大，搜索的随机性也很大，为了加快蚁群的搜索速度，克服算法陷入局部最优，本文引入决策变量的边界自调整策略，研究了一种基于决策变量边界自调整的蚁群算法改进方法.

决策变量的边界自调整策略的原理主要是在算法的迭代寻优过程中，通过对决策变量边界进行自调整，使算法的寻优范围不断向最小适应值附近收敛，以加快收敛速度，克服局部最优.

加入决策变量边界自调整的改进蚁群算法步骤如下:

1)设定决策变量的上下界、决策变量维数、蚂蚁个数.

2)初始化决策变量矩阵，即在决策变量的上下界之间随机产生一个初始化矩阵.

3)开始进行循环，当未达到要求的迭代步数时，决策变量的边界按式(10)、(11)进行自调整:

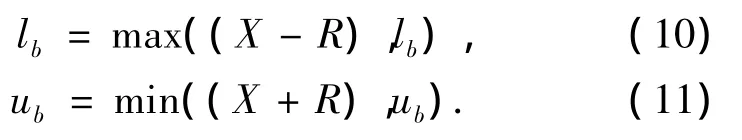
式中:R为一个在(0，1)上随迭代变化的常数，用来控制决策变量的边界.

在迭代寻优过程中，决策变量的边界不断按上述原理进行自调整，这样在寻优的初期，蚁群会在整个决策变量定义域内寻优，搜索范围较大，全局性较好;随着寻优的进行，决策变量的范围逐渐变小，向最优解附近收缩，这样有助于提高算法的寻优速度.

2.4 混合改进蚁群算法

融合上述基于自适应信息素挥发因子、决策变量高斯变异以及决策变量边界自调整3种策略，本文提出了一种混合改进蚁群算法.其程序流程图如图3所示.

混合改进蚁群算法的具体实现步骤如下:

1)初始化.设置蚂蚁个数 m，最大循环次数Ncmax，初始化循环次数Nc和信息素含量.

2)将初始化蚁群放置在路径选择图的初始点.

3)设置循环次数Nc=Nc+1.

4)对所有蚂蚁进行4)～5).

5)选择蚂蚁在下一层到达的节点.此选择按照式(3)、(4)进行.

6)在每只蚂蚁选择好下一层到达的节点后，按照式(5)进行局部信息素的更新.

7)当所有的蚂蚁完成一次循环后，按式(8)更新μ，然后按照式(7)进行全局信息素更新.

8)根据式(10)和(11)进行决策变量边界自调整，调整蚁群搜索范围.

9)根据式(9)对决策变量进行高斯变异.

10)如果循环次数Nc≥Ncmax，即满足结束条件，则循环结束并输出程序计算结果;否则继续.

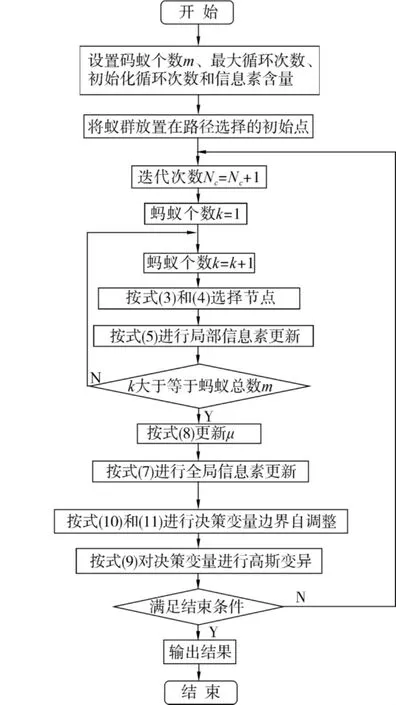
图3 混合改进蚁群算法程序流程Fig.3 Flow chart of hybrid improved ACO

3 混合改进蚁群算法的仿真与分析

本文分别采用 Sphere、DeJongF4、Rosenbrock、Griewank和Rastrigin 5个基准测试函数作为适应度函数，分别应用文献［5］中的基本蚁群算法以及基于信息素挥发因子自适应的蚁群算法、基于决策变量高斯变异和信息素挥发因子自适应的蚁群算法，和基于信息素挥发因子自适应、决策变量高斯变异、决策变量边界自调整三者相融合的混合改进蚁群算法进行仿真实验.其中，参数设置为:蚂蚁个数为30，迭代次数为30，基准函数决策变量为五维，以最大迭代次数作为算法的终止条件，对5个基准函数各进行50次试验.选取字节点上的信息素挥发速度ρ=0.3，Gaussian 分布函数中的参数 σ =0.16.则其仿真结果具体数据见表1和图4～8所示.

表 1中，f1～f5分别代表 Sphere、DeJongF4、Rosenbrock、Griewank和Rastrigin 5个基准测试函数;基本蚁群是指文献［5］的蚁群算法;改进蚁群算法1指基于自适应信息素挥发因子的改进蚁群算法;改进蚁群算法2指基于自适应信息素挥发因子和决策变量高斯变异策略的改进蚁群算法;改进蚁群算法3指基于自适应信息素挥发因子、决策变量高斯变异策略和决策变量边界自调整策略的混合改进蚁群算法.

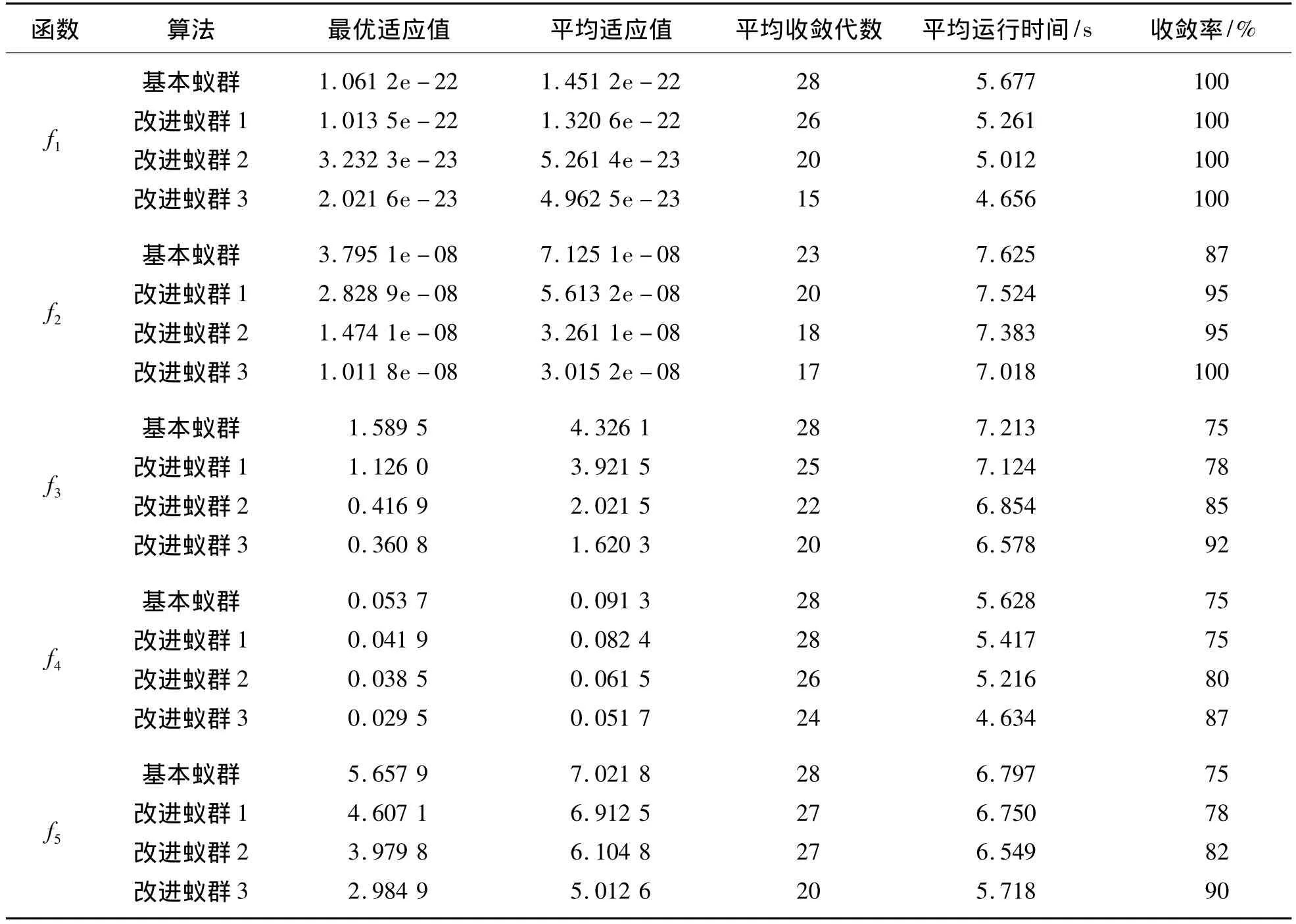
表1 基于5种基准测试函数的蚁群优化仿真结果对比Table 1 Comparison of simulation results using different ACOs based on 5 basic test functions

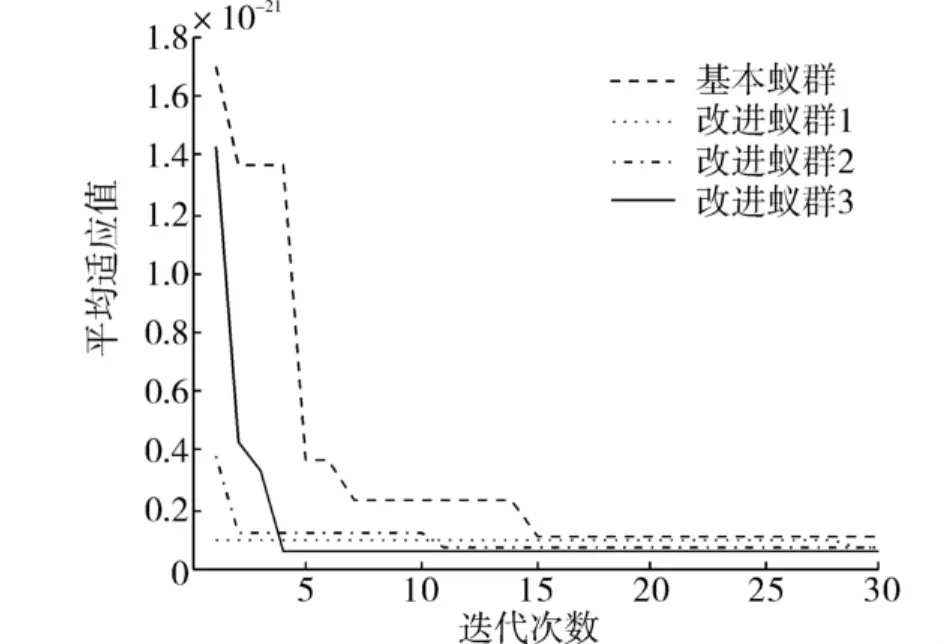
图4 基于Sphere函数的蚁群优化仿真结果Fig.4 Simulation results of ACO based on Sphere function

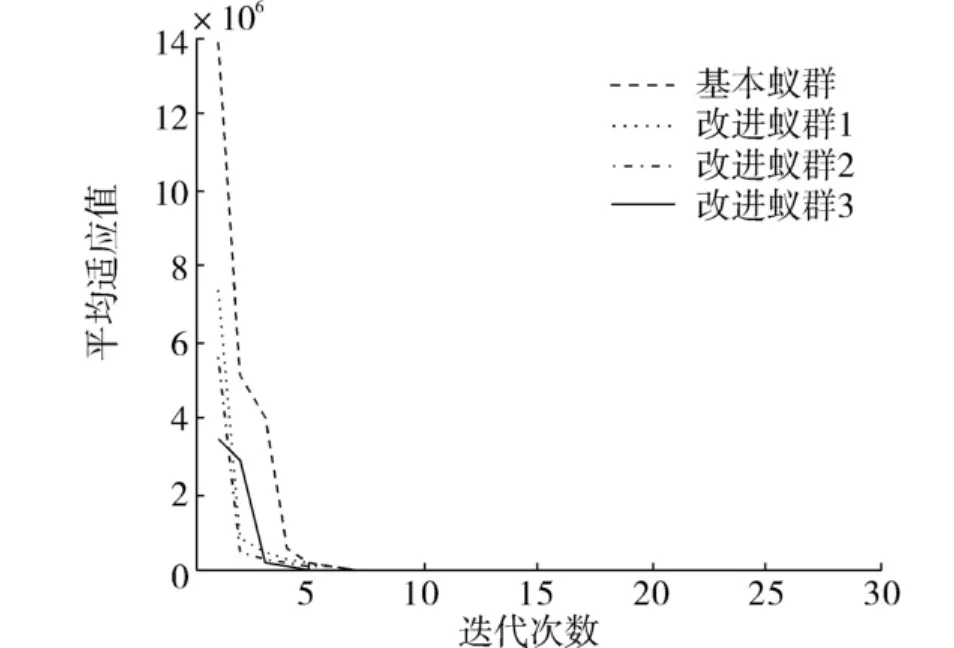
图5 基于DeJongF4函数的蚁群优化仿真结果Fig.5 Simulation results of ACO based on DeJongF4 function

图6 基于Rosenbrock函数的蚁群优化仿真结果Fig.6 Simulation results of ACO based on Rosenbrock function

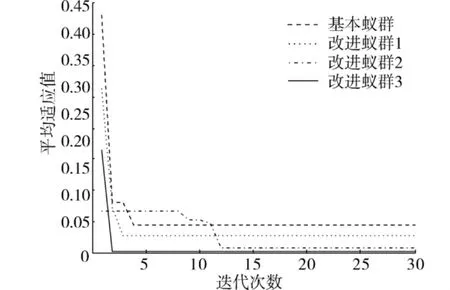
图7 基于Griewank函数的蚁群优化仿真结果Fig.7 Simulation results of ACO based on Griewank function

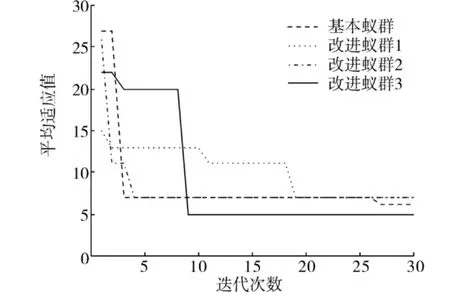
图8 基于Rastrigin函数的蚁群优化仿真结果Fig.8 Simulation results of ACO based on Rastrigin function

根据表1及图4～8的仿真结果可以看出，对比于文献［5］的基本蚁群算法以及本文涉及的单个改进算法，可以得出如下结论:

1)在最优适应值和收敛时间方面，混合改进蚁群算法寻优的精度最高，并且能在最短的运行时间和最少的迭代次数内达到收敛，这是因为加入信息素挥发因子自适应策略和决策变量边界自调整策略，逐渐缩小最优路径和最差路径上的信息量，实现了对决策变量空间的充分寻优.

2)在收敛率方面，在对比较难寻优的DeJongF4函数进行寻优时，混合改进蚁群算法仍然能达到100%的收敛率，对于Griewank和 Rastrigin 2个多峰函数，以及比较难寻优的Rastrigin函数进行寻优时，考虑到函数本身性能的影响，混合改进蚁群算法没有达到100%的收敛率，但是在3种改进蚁群算法中，收敛率也是最高的，这是因为加入决策变量高斯变异策略，改善了蚁群算法的全局搜索能力，避免了局部的早熟现象.

综上所述，本文提出的基于信息素挥发因子自适应、决策变量高斯变异和自变量边界自调整的混合改进蚁群算法在收敛速度和收敛率方面都有很大改进，具有更好的寻优性能.

4 结束语

本文在文献［5］蚁群算法理论的基础上，针对蚁群算法易出现停滞现象、搜索时间长、对寻优解空间搜索不够等不足，提出了一种基于自适应信息素挥发因子、决策变量高斯变异和决策变量边界自调整3种改进策略的混合改进蚁群算法.将该算法应用于函数优化中，通过5个基准测试函数的仿真结果表明，本文提出的混合改进蚁群算法提高了寻优精度，加快了寻优速度，提高了收敛率，具有更好的寻优性能.

［1］DERIGO M，CARO G D.Ant algorithms for discrete optimization［J］.Artificial Life，1999，5(3):137-172.

［2］张纪会，高齐圣，徐心和.自适应蚁群算法［J］.控制理论与应用，2000，17(1):1-8.

ZHANG Jihui，GAO Qisheng，XU Xinhe.Adaptive ant colony optimization［J］.Control Theory and Applications，2000，17(1):1-8.

［3］詹士昌，吴俊.基于蚁群算法的PID参数优化设计［J］.测控技术，2004，23(2):69-71.

ZHAN Shichang，WU Jun.Design of PID optimization based on ACO［J］.Measurement＆ Control Technology，2004，23(2):69-71.

［4］李玉英.混沌蚂蚁群优化算法及其应用研究［D］.北京:北京邮电大学，2009:15-21.

LI Yuying.On chaos ant colony optimization and its application［D］.Beijing:Beijing University of Posts and Tele-communications，2009:15-21.

［5］陈烨.用于连续函数优化的蚁群算法［J］.四川大学学报:工程科学版，2004，36(6):117-120.

CHEN Ye.Ant colony optimization for continuous functions［J］.Journal of Sichuan University:Engineering Science E-dition，2004，36(6):117-120.

［6］陈烨.变尺度混沌蚁群算法［J］.计算机工程与应用，2007，43(3):68-70.

CHEN Ye.On mutative scaled chaos ant colony optimization［J］.Computer Engineering and Applications，2007，43(3):68-70.

［7］王颖，谢剑英.一种自适应蚁群算法及其仿真研究［J］.系统仿真学报，2002，14(1):31-33.

WANG Ying，XIE Jianying.An adaptive ant colony optimization and its simulations［J］.Journal of System Simulation，2002，14(1):31-33.

［8］STUTZLE T，HOOS H H.MAX-MIN ant system［J］.Future Generation Computer Systems，2000，16(8):889-914.

［9］BILCHEV G A，PARMEE I C.The ant colony metaphor for searching continuous space［J］.Lecture Notes in Computer Science，1995，993(1):25-39.

［10］GUTJAHR W J.A graph-based ant system and its convergence［J］.Future Generation Computer System，2000，16(8):873-888.

［11］DREO J，SIARRY P.Continuous interacting ant colony algorithm based on dense heterarchy［J］.Future Generation Computer Systems，2004，20(5):841-856.

［12］周爽，张钧萍，张枫，等.基于蚁群算法的遥感图像聚类方法［J］.哈尔滨工程大学学报，2009，30(2):210-214.

ZHOU Shuang，ZHANG Junping，ZHANG Feng，et al.Clustering method for remote sensing images based on an ant colony algorithm［J］.Journal of Harbin Engineering U-niversity，2009，30(2):210-214.

［13］赵百轶，张利军，贾鹤鸣.基于四叉树和改进蚁群算法的全局路径规划［J］.应用科技，2011，38(10):23-28.

ZHAO Baiyi，ZHANG Lijun，JIA Heming.Global path planning based on quadtree and improved ant colony optimization algorithm［J］.Applied Science and Technology，2011，38(10):23-28.