自适应扩维UKF算法在SINS/GPS组合导航系统中的应用

孙尧，马涛，高延滨，王璐

(1.哈尔滨工程大学自动化学院，黑龙江哈尔滨 150001;2.上海交通大学航空航天学院，上海 200240)

卡尔曼滤波是一种递推的线性无偏最小方差估计，当理论模型与实际系统完全匹配时，卡尔曼滤波器输出的残差序列是互不相关的高斯白噪声序列［1］.然而，其前提是必须精确已知系统模型和噪声的统计特性，否则将会出现滤波器精度下降甚至发散等问题［2］.这是由于当系统噪声统计特性未知时，估计误差的协方差矩阵随时间逐渐收敛于零，状态估计过分依赖于陈旧数据，导致滤波发散［3］.

衰减记忆滤波方法能够通过自适应渐消因子限制滤波器的记忆长度，从而抑制了滤波发散［4］.但是，对高阶系统进行滤波时，由于系统各状态量估计精度的差异，通过简单渐消因子的计算，很难达到理想的效果.针对这一问题，文献［3，5］通过自适应渐消矩阵限制滤波器的记忆长度，但其前提条件为系统状态量是直接可观测的，即系统量测矩阵中对应部分为对角阵，这极大地限制了自适应渐消矩阵在具有复杂量测方程系统中的应用.

传统渐消因子的计算方法以卡尔曼滤波为基础，仅适用于线性系统状态估计，而组合导航系统是典型的非线性系统，由于忽略了高阶误差项，基于线性误差模型的组合导航系统滤波精度将会下降.Julier提出了基于Unscented变换的UKF(unscented Kalman filter)算法［6］，不论系统非线性程度如何，Unscented变换都能以三阶泰勒精度逼近非线性系统状态的后验分布.然而，传统UKF算法假定系统噪声为加性噪声，不参与系统非线性传递，Merwe等针对含有非加性噪声的非线性系统，提出了扩维UKF(augmented UKF，AUKF)算法［7］，文献［8］从理论上给出了AUKF算法可以提高滤波精度的证明.但UKF和AUKF算法与经典卡尔曼滤波器一样，以最小方差估计原理为理论基础，都需要精确已知系统的模型和噪声统计特性.

针对以上分析，提出了带自适应渐消矩阵的AUKF(adaptive fading matrix augmented UKF，AFMAUKF)算法.为了使渐消矩阵适用于具有复杂量测方程的系统，提出一种新的自适应渐消矩阵的计算方法，并以Unscented变换对系统的后验均值和协方差进行近似，从而将自适应渐消矩阵的使用扩展到含有非加性白噪声的非线性系统状态估计领域.

1 渐消矩阵的分析与计算

考虑如下线性离散系统:

文献［3］提出了一种自适应渐消因子卡尔曼滤波(adaptive fading factor Kalman filter，AFF-KF)算法，记为

式中:Q和R分别为系统噪声和量测噪声的协方差矩阵，且Q和R正定.

自适应渐消因子为

式中:

从而得到带自适应渐消因子的误差协方差矩阵一步预测过程为

这种计算渐消因子的方法简单，适用于低阶系统的滤波问题.在高阶系统中，由于各状态量估计精度的差异，使用自适应渐消因子的滤波效果并不理想.

文献［5］通过自适应渐消矩阵对卡尔曼滤波的记忆长度进行限制，记:

自适应渐消矩阵为

该方法的前提条件为系统量测矩阵中对应部分为对角阵，当系统状态量存在耦合关系，或系统状态量不是直接可观测的时候，该计算方法无法使用.且随着时间的推移，Ck+1的计算量会逐渐增大，保存从初始时刻开始的新息矢量对于长时间工作的滤波器来说也是很难实现的.

针对以上问题，本文根据滤波最优的条件，提出一种自适应渐消矩阵的计算方法.

若k时刻滤波最优，根据卡尔曼滤波的无偏性和正交性原理，残差应服从均值为0的高斯分布，即

由式(3)构造残差的加权平方和:

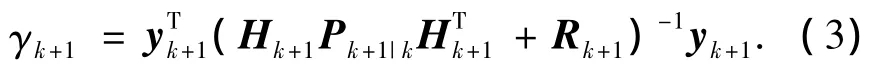
根据χ2分布的定义，γk+1服从m自由度的中心χ2分布.通过自适应渐消矩阵对一步预测误差协方差矩阵的修正过程同式(1)，根据式(1)可以看出，Sk+1无法通过直接计算获得.假设Ωk+1Hk+1=Hk+1Sk+1，则有

根据χ2检验准则，得到Ωk+1的计算方法:

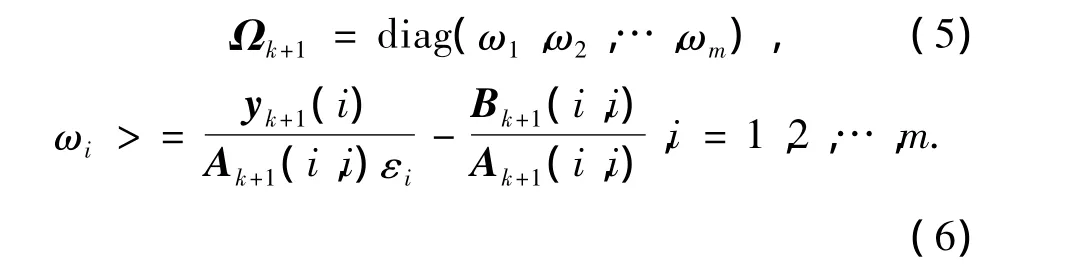
式中:Ak+1和Bk+1的计算方法同式(1).

假设Hk+1是行满秩的.当Hk+1不存在全零列时，自适应渐消矩阵为

从而通过式(7)得到经自适应渐消矩阵修正后的一步预测误差协方差矩阵.

在组合导航系统中Hk+1存在全零列的情况十分常见，此时假设系统状态维数为n，系统观测量维数为m，Hk+1中全零列的维数为p，将Hk+1表达为如式(8):

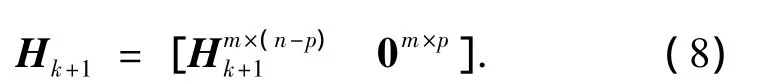
渐消因子矩阵的计算过程为:

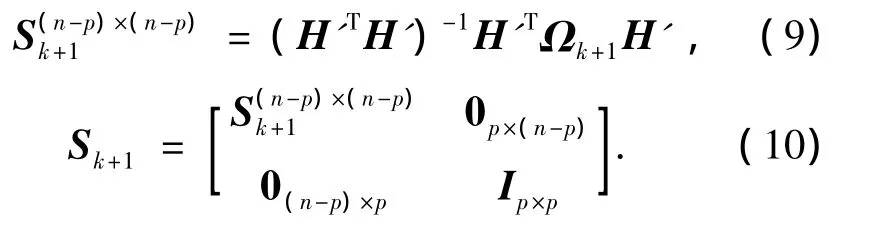
2 AFM在UKF算法中的等价描述

通过以上分析可以看出，计算自适应渐消因子和渐消矩阵的方法都是基于卡尔曼滤波框架的，需要获得系统的状态转移矩阵和量测矩阵等信息.然而，在AUKF算法中，状态转移矩阵和量测矩阵等系统信息无法直接获得;因此，无法通过卡尔曼滤波框架下的计算方法得到AUKF滤波器的自适应渐消矩阵.由于AUKF与UKF算法在原理上是相同的，因此，通过UKF的等价描述，可以得到AUKF滤波器自适应渐消矩阵的计算方法.

根据卡尔曼滤波和UKF算法的等价描述［9］:

可以得到计算自适应渐消矩阵过程中各变量的表达式为

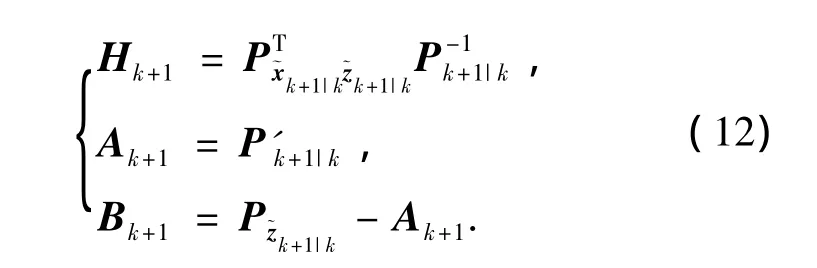
式中:P'k+1|k为系统误差的协方差矩阵沿非线性函数的传播结果，计算P'k+1|k的步骤与UKF算法中计算Pk+1|k的步骤相似，只是计算Sigma点沿非线性函数的传播过程的时候，不考虑系统噪声的作用即可.显然，对于系统噪声为加性白噪声的非线性系统，有Qk=Pk+1|k－P'k+1|k.

针对自适应渐消矩阵的计算，当Hk+1不存在全零列时，可由式(5)～(7)获得;否则，采用式(5)、(6)、(8)～(10).在此基础上，可以得到经自适应渐消矩阵修正后的一步预测协方差矩阵为

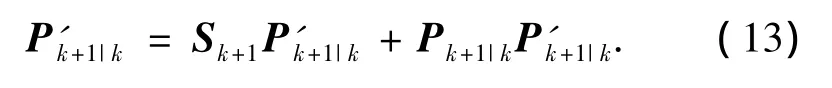
3 AFM-AUKF算法

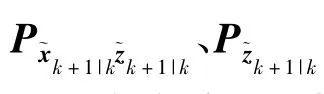
考虑如下非加性噪声的非线性离散系统:

式中:k≥0为离散时间变量;x∈Rn为状态向量;u∈Rn为输入向量;z∈Rm为输出向量;非线性函数f∈Rq× Rn→Rn，h∈Rn→Rm.系统噪声 vk、量测噪声wk分别为q维和m维的高斯白噪声，并具有以下统计特性:

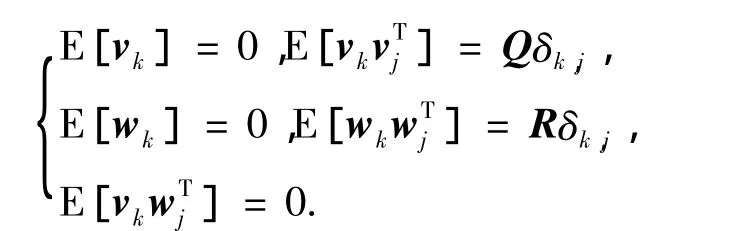
式中:Q 和 R 为正定对称阵，δk，j为 kronecker-δ函数.

初始化系统状态和误差的协方差矩阵为

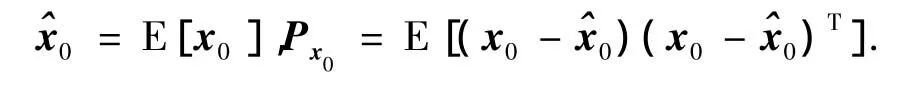
根据自适应渐消矩阵在UKF算法中的等价计算方法，得到AFM-AUKF算法的步骤:

1)计算Sigma点.

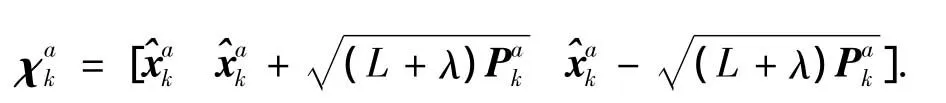
式中:L=n+q+m为扩维后的系统状态维数.

2)权值计算.

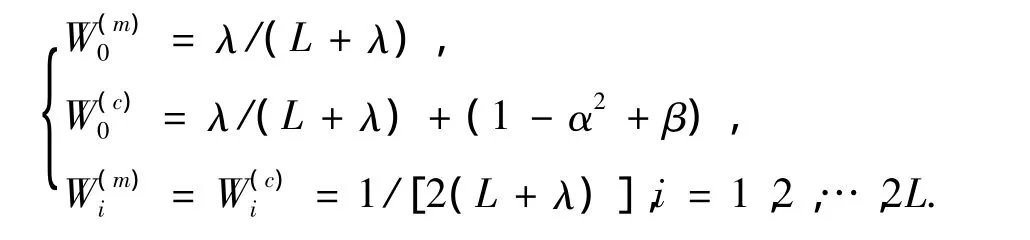
式中:λ=α2(L+k)－L.

3)时间更新过程.

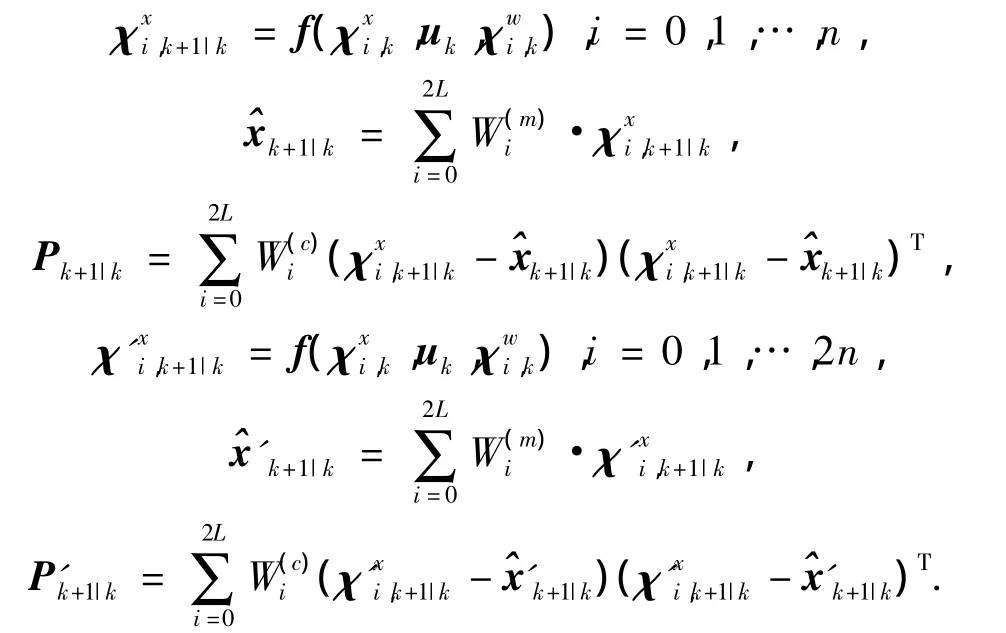
4)量测更新过程.

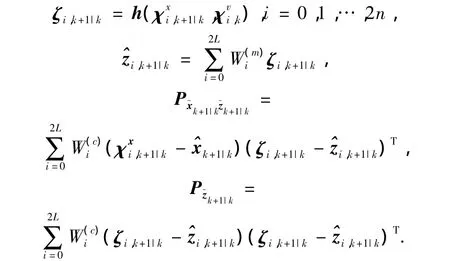
5)重新计算Sigma点.

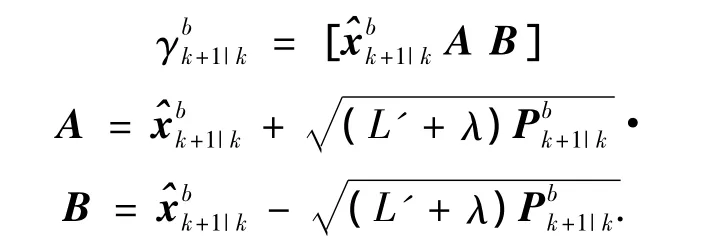
6)新的Sigma点权值计算.

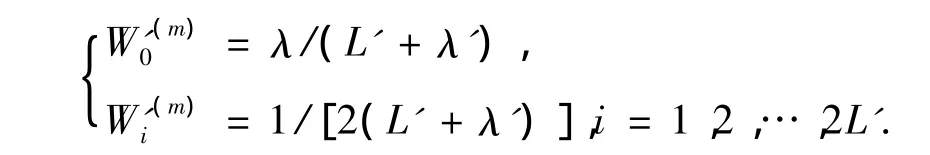
式中:λ'=α2(L'+k)－L'.

7)经渐消矩阵修正后的量测更新.

8)最小方差估计结果.

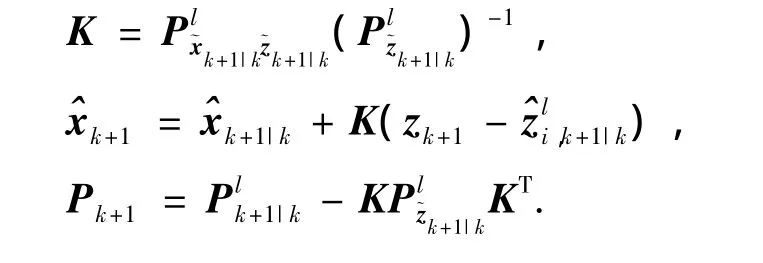
4 实验与分析

为了验证AFM-UKF算法的性能，本文以SINS/GPS组合导航系统作为平台，对提出的方法进行验证.选取北、东、地坐标系作为导航坐标系，取姿态四元数、速度、位置和陀螺零偏作为系统状态向量，建立滤波器状态方程，选取位置、速度为系统观测向量，建立滤波器量测方程，具体模型参考文献［11］.

分别采用UKF、自适应渐消因子的扩维UKF(adaptive fading factor augmented UKF，AFF-AUKF)和AFM-AUKF作为滤波器对组合导航系统的姿态、速度和位置信息进行估计.通过系统状态突变、系统噪声统计特性不准确和加速度计噪声统计特性不准确3个试验验证3种滤波方法对系统模型不确定的鲁棒性和容错能力.

4.1 系统状态突变

采用静态数据进行试验，并在t=30 s时，设定系统的俯仰角和横滚角误差突变为－10°，检验滤波器的容错能力(如图1～3).通过试验结果可以看出，AFF-AUKF和AFM-UKF算法与传统UKF算法相比，姿态误差的均值分别降低了44.6%和83.2%，姿态误差的标准差分别降低了32.4%和54.9%.

图1 系统状态突变时的姿态误差Fig.1 Attitude error of state mutation

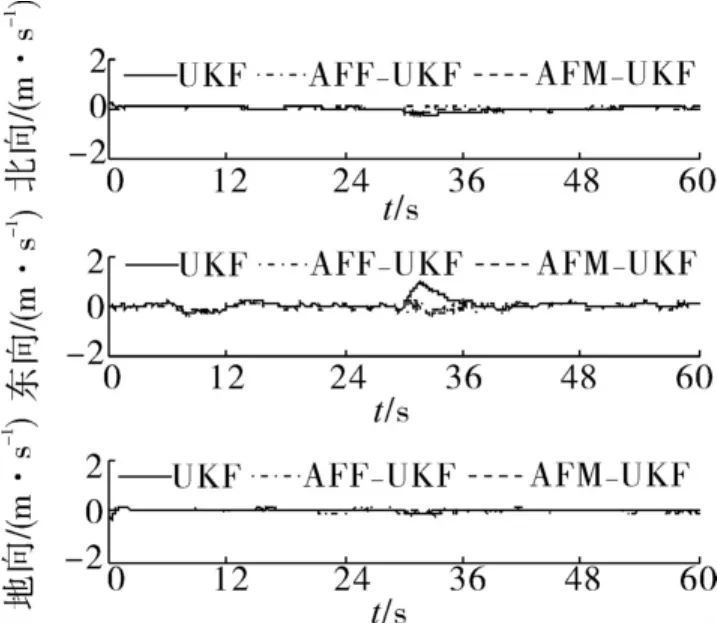
图2 系统状态突变时的速度误差Fig.2 Velocity error of state mutation

图3 系统状态突变时的位置误差Fig.3 Position error of state mutation

4.2 系统噪声统计特性不准确

使用摇摆数据进行试验，假设在t=30 s时，系统噪声的统计特性发生突变，陀螺仪和加速度计噪声的方差均变为原来的100倍(如图4).此时，AFFUKF和AFM-UKF算法与传统UKF算法相比，姿态误差的均值分别降低了54.4%和71.6%，姿态误差的标准差分别降低了59.6%和90.6%.

图4 系统噪声不准确时的位置误差Fig.4 Attitude error while the statistics of system noise is inaccurate

4.3 加速度计噪声统计特性不准确

使用摇摆数据进行试验，假设在t=30 s时，系统噪声的统计特性发生突变，但仅有加速度计噪声的方差变为原来的100倍，而陀螺的噪声统计特性不发生改变(如图5所示).此时，AFF-UKF和AFMUKF算法与传统UKF算法相比，姿态误差的均值分别降低了7.0%和78.3%，姿态误差的标准差分别降低了2.6%和88.1%，

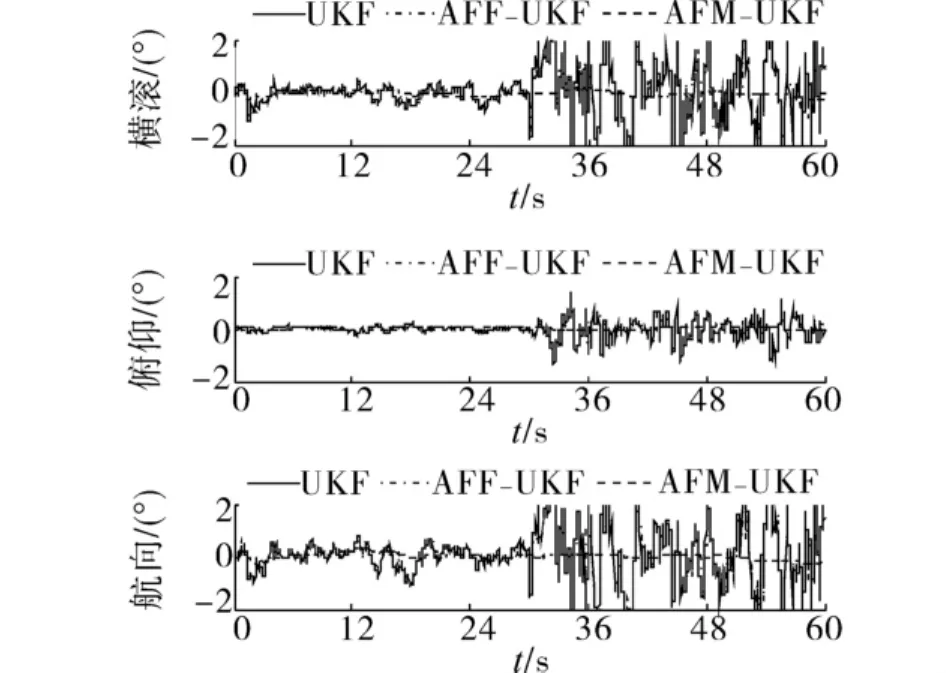
图5 加速度计噪声统计特性不准确时的位置误差Fig.5 Attitude error while the noise’s statistics of accelerometer is inaccurate

4.4 结果分析

从以上实验结果可以看出，由于系统的速度和位置状态量是直接可观测的，所以3种方法在位置和速度估计效果上的差异并不明显，只是AFM-UKF算法的位置估计精度略高于AFF-UKF算法和传统UKF算法.但是通过表1中数据的比较能够看出:在系统状态突变时，2种衰减记忆方法对突变状态的跟踪能力均强于传统UKF算法，AFM-UKF算法的跟踪速度又略高于AFF-UKF算法;在系统噪声全部发生改变且变化幅度一致时，AFF-UKF和AFM-UKF算法均能够提高姿态估计的精度，并且AFMUKF算法精度高于AFF-UKF算法;但当系统噪声中各部分变化不一致时，由于噪声统计特性精度的差异，AFF-UKF算法的滤波精度受到极大的影响，系统精度的改善不明显，而AFM-UKF算法的精度远远高于UKF算法和AFF-UKF算法的精度，可见，AFM-UKF算法对于系统模型不确定性具有更强的鲁棒性.

表1 UKF、AFF-UKF和AFM-UKF算法实验结果精度比较Table 1 Filtering precision of UKF，AFF-UKF and AFM-UKF of experimental results (°)

5 结束语

本文提出的带自适应渐消矩阵的扩维UKF算法，有效地解决了含有非加性白噪声的非线性系统在系统状态存在突变和系统噪声统计特性不准确时的滤波问题.实验结果表明，AFM-AUKF算法不仅与传统UKF算法相比，具有更强的鲁棒性和更高的滤波精度;而且与AFF-AUKF算法相比，AFM-AUKF算法对于噪声统计特性的变化鲁棒性更强，尤其对于部分噪声统计特性发生变化时，由于渐消矩阵的灵活性，使算法具有更强的容错能力.

［1］CHUI C K，CHEN G.Kalman filtering with real-time applications［M］.4th ed.New York:Springer-Verlag，2009:20-28.

［2］HAJIYEV C.Adaptive filtration algorithm with the filter gain correction applied to integrated INS/Radar altimeter［J］.Journal of Aerospace Engineering，2007，221(5):847-855.

［3］耿延睿，崔中兴，张洪钺，等.衰减因子自适应滤波及在组合导航中的应用［J］.北京航空航天大学学报，2004，30(5):434-437.

GENG Yanrui，CUI Zhongxin，ZHANG Hongyue，et al.A-daptive fading Kalman filter with applications in integrated navigation system［J］.Journal of Beijing University of Aeronautics and Astronautics，2004，30(5):434-437.

［4］夏启军，孙优贤，周春晖.渐消卡尔曼滤波器的最佳自适应算法及其应用［J］.自动化学报，1990，16(3):210-216.XIA Qijun，SUN Youxian，ZHOU Chunhui.An optimal adaptive algorithm for fading Kalman filter and its application［J］.Acta Automatica Sinica，1990，16(3):210-216.

［5］高青伟，赵国荣，吴芳，等.衰减记忆自适应滤波在惯导系统传递对准中的应用［J］.系统工程与电子技术，2010，32(12):2648-2651.

GAO Qingwei，ZHAO Guorong，WU Fang，et al.Application of adaptive fading filter technique in transfer alignment of inertial navigation systems［J］.Systems Engineering and Electronics，2010，32(12):2648-2651.

［6］JULIER S，UHLMANN J K，DURRANT-WHYTE H F.A new approach for filtering nonlinear system［C］//Proceedings of the American Control Conference.Seattle，USA，1995:1628-1632.

［7］MERWE R.Sigma-point Kalman filters for probabilistic inference in dynamic state-space models［D］.Portland，USA:Oregon Health and Science University，2004:108-125.

［8］BRIERS M，MASKELL S R，WRIGHT R.A Rao-Blackwellised unscented Kalman filter［C］//Proceedings of the 6th International Conference of Information Fusion.Cairns，Australia，2003:55-61.

［9］王小旭，赵琳，夏全喜，等.基于Unscented变换的强跟踪滤波器［J］.控制与决策，2010，24(7):1063-1068.

WANG Xiaoxu，ZHAO Lin，XIA Quanxi，et al.Strong tracking filter based on unscented transformation［J］.Control and Decision，2010，24(7):1063-1068.

［10］霍成立，谢凡，秦世引.面向室内移动机器人的无迹滤波实时导航方法［J］.智能系统学报，2009，4(4):295-302.

HUO Chengli，XIE Fan，QIN Shiyin.A case study in real-time UKF-based navigation for indoor autonomous travelof mobile robots［J］.CAAI Transactions on Intelligent Systems，2009，4(4):295-302.

［11］Van der MERWE R，WAN E A.Sigma-point Kalman filters for integrated navigation［C］//Proceedings of the 60th Annual Meeting of The Institute of Navigation.Dayton，USA，2004:641-654.