基于小波分析的低信噪比天气雷达回波弱信号提取

李 华, 高玉春, 柳云雷

（1.成都信息工程学院,四川成都 610225;2.中国气象局气象探测中心,北京 100081）

0 引言

在现代天气雷达的探测过程中,雷达接收机输出的回波信号不仅包括探测到的气象回波信号,同时也包含很多噪声,甚至有时噪声几乎淹没了有用信号。有用信号和噪声信号夹杂在一起,通常给雷达数据带来很多杂质。噪声的存在对目标信号的精确分析也有严重的影响。因此必须想办法从这种低信噪比的雷达回波信号中消除噪声,提高回波信号的信噪比,为正确识别目标信号提供有利条件。

对天气雷达弱信号的提取实质就是对信号进行去噪处理,其目的是消除噪声,将有用信号从强噪声背景中提取出来,或者用一些新技术和新方法提高检测系统输出信号的信噪比。对微弱信号检测理论与方法的研究,是目前雷达信号处理领域的一个热点,前人已经提出不少检测和提取弱信号的算法,并不断加以改进[1]。

1 雷达回波信号去噪方法简介

在信号处理中,用于提高信号的信噪比并提取弱信号的方法有很多,并且一直在不断改进和发展中。传统的方法分为时域方法和频域方法,经典时域方法指的是时域平均算法[2],是一种积累平均抗干扰过程,算法实现简单,但是抗噪性能很差。经典频域方法就是快速傅里叶变换（FFT）,该算法认为信号普遍表现为低频而噪声表现为高频,将信号进行FFT以后再用低通滤波器进行滤波。在实际工程应用中通常采用FIR滤波器对信号进行滤波,但是如果滤波器的窗函数选择不当,有时会滤除掉有用信号[3]。这两种方法对雷达回波信号进行处理显得有些片面,时域平均算法只采取了信号的时域特征忽略了频域值这个度量,FFT算法虽然把频域和时域结合起来分析回波信号,但是它属于全局变换,不能有机地将时频域结合起来,其抗噪性能同样不佳。

小波分析是当前应用数学中数字处理的一个迅速发展的新领域[4],在信号处理中得到广泛的应用。该分析方法是对信号同时在时域和频域进行分析,将时域和频域有机的结合。小波分析的实质是把原始信号不同频率段的信息抽取出来,并将其显示于时间轴上,这样既可反映信号的时域特征也可反映信号的频域特征。在雷达回波信号处理中引入小波分析的算法,能更好地进行信号去噪处理,提高信噪比从而提取弱信号,为后续的雷达数据处理奠定良好的基础,提供更高质量的数据来源。

2 小波去噪原理及方法简介

2.1 小波变换简介

设平方可积函数 f（t）的连续小波变换定义为[5]:

小波能够消噪主要由于小波变换具有如下特点[6]:

（1）低熵性。小波系数的稀疏分布,使信号处理后的熵降低。

（2）多分辨特性。由于采用了多分辨的方法,所以可以非常好地描述信号的非平稳性,如突变和断点等,可以在不同分辨率根据信号和噪声的分布去除噪声。

（3）去相关性。小波变换可对信号去相关,且噪声在变换后有白化趋势,所以小波域比时域更有利于去噪。

（4）基函数选择灵活。小波变换可以灵活选择基函数,也可以根据信号特点和降噪要求选择多带小波、小波包等,对不同的场合,可以选择不同的小波基函数。

2.2 小波去噪简介

设雷达回波信号由两部分组成,则一个被噪声污染的雷达回波信号模型可表示为[7-8]:

其中,x（t）表示有用信号,n（t）表示一个[0,δ2]的随机噪声,s（t）是采集到的雷达回波信号。对（2）式两边做小波变换,有

小波变换是线性变换,即两个信号和的小波变换等于各个信号小波变换之和,两个信号之和的小波系数是各个信号的小波系数之和。噪声对信号的影响主要表现在小波系数的各个尺度上,而目标信号的主要特征却分布在较大的有限的几个系数上。这时,就可以采用相应的准则对信号和噪声的小波变换系数进行处理。处理的实质在于减小乃至完全剔除噪声产生的小波系数,同时最大限度的保留有效信号产生的小波系数,然后再用处理后的系数重构信号[9]。

对雷达回波信号进行去噪的模型如图1所示。

其过程可分为以下3个步骤:

（1）对信号进行小波分解。选择一个小波基函数并确定分解层次N,再进行分解运算。

（2）小波分解系数的阈值量化。选择相应的阈值以及阈值规则对小波分解的各层高频系数进行阈值化处理,小波分解的第 N层低频系数一般不做处理。

（3）信号重构。根据小波分解的第 N层低频系数和经过阈值处理的1～N层的高频系数进行小波重构,从而达到去噪并提取弱信号的目的。

图1 基于小波分析的信号去噪框图

3 小波分析过程

小波分析去噪总体框图如图2所示。

（1）选取小波函数。不同的小波基函数的消噪结果差异性较大。经过多次反复试验,文中采用db6小波,该小波不仅具有紧支撑集,而且有近似对称并正交,使用它不仅可减少计算量,而且计算结果比较精确。

（2）分解层数确定。信号和噪声在不同尺度的小波变换下呈现的特性截然相反,即随着尺度的增大,信号和噪声所对应的小波变换系数分别是增大和减小。因此,连续做若干次小波变换之后,由噪声对应的小波变换系数已基本去除或幅值很小,而所余系数主要由信号控制。经过多次仿真实验证,作6层分解效果比较理想。

图2 小波去噪框图

（3）阈值选取[10]。在进行阈值去噪的时候,阈值的选择对消噪结果具有决定性的意义。阈值选取不当,有时会把信号当作噪声滤除,有时会把小波系数较大的噪声误认为信号留下。由于在不同的信噪比条件下,噪声和信号强度表现不同。所以,根据不同的信噪比范围对阈值采取不同的算法,将信噪比划分为两个区间:SNR≥0和SNR＜0。对于不同的区间采取不同的阈值。具体阈值形式如下:

（i）当信噪比大于0时,意味着混合信号中信号的能量比噪声的能量大,信号占主体部分。这时阈值选取如果过大就容易将信号本身产生的小波系数当成噪声而滤除,而且也会平滑掉信号的细节部分,因此阈值选取为:

其中,σn表示噪声的标准差,N表示小波系数的长度,j为当前的分解层数。

（ii）当信噪比小于0时,意味着混合信号中噪声的能量比噪声的能量大。混合信号中有用信号强度减小或者噪声强度增大时,信噪比均会减小。如果还是利用（i）中的方法确定阈值,只是片面地利用噪声强度区分噪声和有用信号,会造成阈值过大从而滤除掉更多的信息,重构后的信号基本处于一条平滑的直线,无法提取有效信息。因此,当信噪比较低时,阈值的选取应该从噪声和信号中进行权衡:

其中,σn表示噪声的标准差,σs表示信号的标准差,N表示小波系数的长度,j为当前的分解层数。

其中,参数a用以调整随着σn/σs的变化,针对不同的信噪比a的取值不同。经过大量统计分析,在信噪比为-10dB时取0.85去噪效果最佳。

（4）阈值处理。确定阈值后,对小波系数的阈值处理对重构信号的还原度也有着重大意义。在小波分析方法中,一般软阈值比硬阈值的消噪结果平滑,而分层阈值又比全局阈值结果更精确。所以,采用分层软阈值,即针对每层小波确定不同的软阈值进行消噪处理。阈值处理方式如下:

4 仿真结果分析

在MATLAB下用上述仿真方法仿真天气雷达回波信号,其中参数设置为:波长 λ=10cm,采样频率 fs=1000Hz,速度v=10m/s。将噪声按照一定的信噪比加到原始回波信号中[11-12],再用小波分析的方法对其进行去噪处理。对于天气雷达回波信号来说,信噪比小于1dB可视为小信号,-10dB,-20dB甚至更低的信噪比可视为弱信号。所以,采用-10～10dB的输入信噪比分析该仿真信号在小波分析方法下的信噪比输出和信噪比改善。

仿真的天气雷达回波I路信号和Q路信号以及对应的功率谱密度如图3、图4所示。

图3 I/Q信号时域波形

图4 I/Q信号功率谱密度函数

图5 SNR=-10dB I/Q信号时域波形

图6 SNR=-10dB I/Q信号功率谱密度

如图6所示,按照一定的信噪比（SNR=-10dB）加入噪声后生成带噪声的雷达回波功率谱密度,该功率谱密度不仅包含原始雷达回波的全部频率信息还包括所加的噪声信息。由图5～6可知,不管从频域还是时域看,噪声对原始雷达回波信号已造成强烈的干扰,在雷达回波功率谱中出现较多的随机分量,在进行谱矩估计的时候根本无法提取出有效信息。

为了体现小波分析在低信噪比背景下对弱信号提取的有效性和优越性,针对仿真试验中的带噪信号,分别用小波分析的方法和FIR滤波器对其进行去噪处理得到结果如图7～8所示。其中,FIR滤波器的通带和阻带边界频率分别为100Hz/和300Hz,并使用哈明窗求得最小阶数为63。

图7 小波分析去噪后时域波形

图8 FIR滤波器去噪后时域波形

图9 小波分析去噪后功率谱密度

图10 FIR滤波器去噪后功率谱密度

当SNR=-10dB时,从时域看,小波分析方法比FIR滤波器优势更为突出。信号的边缘比较平滑,细节部分比较明显,对信号突变点的检测更清晰,总体特征更接近原始信号;从频域看,经小波分析处理后的功率谱密度在f=200Hz处有明显的峰值,对噪声的抑制也比较可观,而经FIR滤波器处理后的信号功率谱密度峰值不如小波分析后的明显,对噪声的抑制不理想,有多峰的情况出现。经小波分析去噪后信号的信噪比为-0.0325dB,提高了9.9675dB,经FIR滤波器去噪后的信噪比为-6.0615dB,提高了3.9385dB。由于文中仿真信号大量采用了随机序列,所以程序每次运行出的结果有一定的波动性。

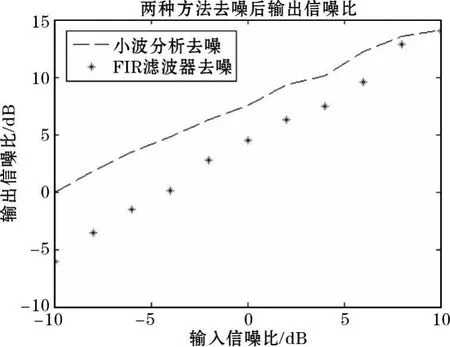
图11 两种方法去噪后的信噪比输出图

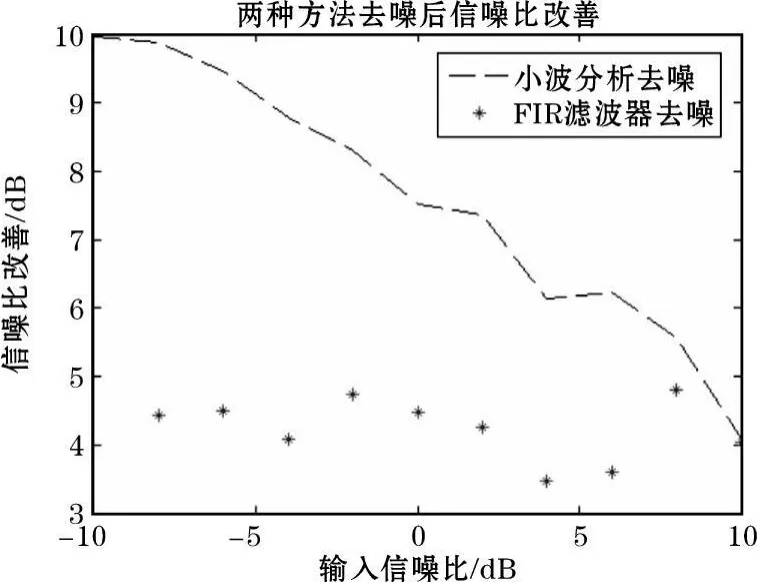
图12 两种方法去噪后的信噪比改善

如图11～12所示,定量分析两种方法在不同信噪比条件下对带噪信号的去噪效果。由图11可知,在低信噪比条件下,小波分析比FIR滤波器效果更为显著。经小波分析后普遍能把信号的信噪比提高4～10dB,FIR滤波器平均能提高4dB。从信噪比改善的图形看,随着信噪比增大,小波分析的去噪能力与FIR滤波器的去噪能力逐渐持平,在SNR=10dB时基本和FIR滤波器一致。

5 结束语

在低信噪比条件下,研究天气雷达回波信号的消噪方法。首先对含噪雷达I/Q信号采用两种不同的方法去噪,从定量和定性两个方面分析两种方法下信号的输出信噪比和信噪比改善等指标,体现小波分析在去噪方面的优势。结果表明小波分析方法能很好地从低信噪比环境下的原始信号中有效地提取出有用信号,可提高信噪比4～10dB。因此,小波分析的方法确实可以用于低信噪比雷达回波信号的去噪。小波分析的方法抗噪性能虽然很好,但是算法比时域平均算法和傅里叶算法都复杂,实时性能也相对较差。因此,在实际工程应用中,对小波分析算法进行改进以提高其实时性能的同时,也可以采用与其他算法相结合的方式来弥补这些不足。

[1] 夏均忠,刘远宏,冷永刚,等.微弱信号检测方法的现状分析[J].噪声与振动控制,2011,6（3）:156-161.

[2] 陈韶华,相敬林.一种改进的时域平均法检测微弱信号研究[J].探测与控制学报,2003,25（4）:56-59.

[3] 张威,王旭,葛琳琳.一种强噪声背景下的微弱信号检测的新方法[J].计量学报,2007,28（1）:70-73.

[4] 郭彤颖,吴成东,曲道奎.小波变换理论应用进展[J].信息与控制,2004,33（1）:67-71.

[5] 简涛,何友,苏峰.小波变换在雷达信号检测中的应用[J].海军航空工程学院院报,2006,21（1）:121-126.[6] 刘正平,冯召勇,杨卫平.基于小波去噪的微弱信号提取[J].制造业自动化.2010,32（8）:98-101.

[7] 黄小毛,张永刚.小波变换在雷达回波信号消噪处理中的应用[J].现代雷达,2001,（5）:34-37.

[8] 向东.强噪声背景下弱信号特征提取的小波分析[D].武汉:武汉大学,2003.

[9] 马晓岩,李广柱,张贤达.基于小波变换的雷达信噪比改善分析[J].清华大学学报,2003,43（3）:36-38.

[10] 薛伟,关福宏,陈良章,等.基于一种新的小波阈值函数的雷达回波信号去噪.计算机仿真,2008,25（8）:319-322.

[11] Zrnic S D.Simulation of weatherlike doppler spectra and signals[J].Notes and Correspondence,1975,14（6）:619-620.

[12] 肖大雪.Matlab小波分析在信号处理中的应用[J].科技广场.2011,（1）:60-64.