有噪声条件下神经元编码的预测

李鹏

山东科技大学理学院， 山东 青岛 266590

有噪声条件下神经元编码的预测

李鹏

山东科技大学理学院， 山东 青岛 266590

以Hodgkin-Huxley模型为例，通过分析神经元的峰电位间隔（ISI）来研究神经元的编码预测。对于神经元系统来说，噪声对系统的发放起了重要的作用。在有噪声的情况下，弱的信号可以使神经元产生发放。在某个噪声强度下可以使神经元的ISI序列的非线性预测误差（NPE）达到最小值，从而提高神经元的预测能力。

噪声；神经元；编码；峰电位间隔；非线性预测误差

多数的神经元都用动作电位传递信息。动作电位序列包含了生物编码信息。对于一个时间序列，我们可以来对它进行预测，从而来研究信息编码。对于一个确定性系统来说，由于它具有规则的行为，所以对于他的预测非常容易。对于一个混沌系统行为的预测就比较复杂。有研究指出，在神经元的信息传递过程中，可以用神经元的峰电位间隔（ISI）来研究神经元的编码行为，当一个混沌信号通过一个神经元转换为一个spike train时，系统的动力学性质被保留。这里我们使用非线性预测的方法来分析混沌驱动的神经元的编码行为，用由Sauer提出的非线性预测误差（NPE）来分析噪声对神经元编码预测的影响。这种方法并不要求需要许多的数据点，但是我们所得到的数据点必需是非常有用的。

1、模型

我们使用Hodgkin-Huxley（HH）模型。HH模型是1952年Hodgkin和Huxley在多年的实验数据和电缆理论及中心导体理论的基础上提出来的。它是神经生物学里对动作电位发放描述最准确的经典模型。是一种应用广泛的模型。由以下四个耦合的非线性一阶微分方程描述：

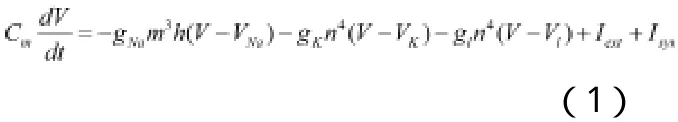
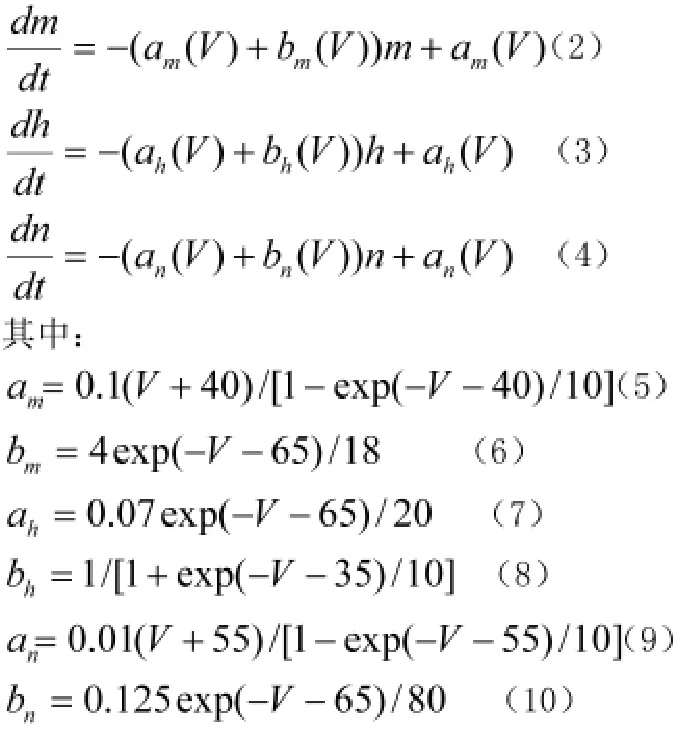
V为神经元的膜电位，m,h为控制Na离子通道的门参数(gating variable)，n为控制K离子通道的门参数；VNa=50mV，Vk=-77mV分别为Na、K离子通道的反转电势， VL=-54.5mV为漏电流的反转电势；相应的最大电导为gNa=120mS/cm2，gK=36mS/cm2，gL=0.3mS/cm2；突触电导为，其中A是最大的突出电导，t0是突触的特征时间。C=1μF/cm2为膜电容。Iext是外部刺激电流，Isyn是突触电流。它是一种自兴奋性系统，对于输入的DC电流I0，发放阈值是Ic≈6.2μA/cm2。当I0＜Ic时，由于稳定的固定点是系统的全局吸引子，所以膜电位显示出一种衰减的阈下振荡。当I0≥Ic时，HH神经元会发生周期的连续的发放。HH神经元对噪声非常敏感，弱的噪声就可以使膜电位在发放阈值附近产生波动，显示了持续的阈下共振。Fig.1描述了在加入噪声的情况下HH神经元的发放情况。其中输入电流为I0≈-2μA/cm2。

2、预测法则

我们使用非线性预测误差的方法对HH神经元的编码行为进行预测。非线性预测误差NPE[2,3]是首先由Sauer提出的。给定一个ISI向量V0={ti0,…,tio-m+1}，选择其他1%个最接近向量V0的重构向量Vk。将来的h步的ISI的数值是对所有的k的平均值，我们用这个平均值来做预测。平均值pi0=〈pik+h〉k应该接近于将来的间隔tio+h。差值p-tio+h是i0的 h步的预测误差。我们也可以用整个序列的平均值m来做预测，同样得到h步的预测误差为m-tio+h。这两个值的均方根的比率给出了我们非线性预测误差NPE，定义式为：

式中的中括号表示对整个序列作平均。NPE是对ISI序列的预测能力的测量。NPE小于1意味着由序列的线性或非线性预测能力超过了序列平均值的基线预测。

3、输入混沌信号的HH模型的NPE

在这里我们方程（1）中的Isyn=0，Iext=S(t)+Inoise。其中Inoise是色噪声，其表达式为：

其中ξ(t)表示高斯白噪声，D是噪声强度，τd是关联时间。 是输入的混沌信号，由Lorenz[4]模型来产生。

NPE的计算法则在二中已经给出，我们由此来计算HH序列的NPE。Fig.2给出了由HH模型得到的ISI序列的NPE。在没有噪声的时候，没有尖峰产生。随着噪声强度的增加，在小噪声的情况下开始有尖峰电位的发放，但是ISI序列没有表现出可预测的能力NPE≈1。直到噪声强度D=1时，才表现出来可预测的性质。随着噪声强度的增加，直到噪声强度大到可以驱动系统的时候，预测误差开始下降到最小值然后又开始上升。由于小的噪声的输入使预测的能力明显的提高本质上是一个随机共振的效用。结果显示了一个非线性决定论的证据。

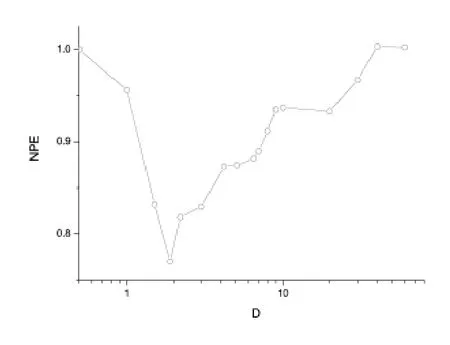
图2 HH模型产生的尖峰序列的NPE与输入噪声的关系

4、结语

通过HH模型引起尖峰电位意味着利用了在吸引子信号中高度非线性过滤的模式，这种过滤模式删除了振幅信息，使整个信息转换成时间事件。目的是得到在通过尖峰时间传递信息的系统中的数据处理的方法。通过我们的例子我们发现，在此过程中噪声的意义重大，噪声可以增强确定性的传递。在输入混沌信号的情况下，噪声可以使神经元的发放从无到有，在某个噪声强度下可以使神经元的ISI序列的预测误差达到最小值，从而提高神经元的预测能力。结果显示了一个非线性决定论。

[1]A.L.Hodgkin, and A.F.Huxley, J.Physiol.(Lond) 117, 500 (1952).

[2]Tim Sauer, Phys.Rev.Lett.72, 3811 (1994).

[3]Tim Sauer, Chaos, 5, 127 (1995).

[4]E.Lorenz, J.Atmos.Sci.20, 130～141(1963).

图1 加入噪声时HH神经元的发放

I0≈-2μA/cm2，噪声强度为上图D=0.5，下图D=1

Predictability in neuronal encoding with noise

Li Peng
College of science, SDUST,Qingdao,Shandong,266590,China

A

O415;Q61

10.3969/j.issn.1001-8972.2012.17.012

山东科技大学科学研究“春蕾计划”(No.2009AZZ070)

李鹏(1980－),男,硕士,讲师,研究方向：软物质与生物物理。

AbstractBy analyze the interspike interval, we study the information encoding of Hodgkin-Huxley neural system.Noise is important for neuron system.In the presence of noise, the neuron produces firing with small signal, the nonlinear prediction error (NPE) of neuron system have the minimun value.

Keywordsnoise; neuron; encoding; interspike interval; nonlinear prediction error