连续时间系统的s域分析及MATLAB实现
张登奇, 张 璇
(1. 湖南理工学院 信息与通信工程学院, 湖南 岳阳 414006; 2. 湖南大学 信息科学与工程学院, 长沙 410082)
连续时间系统的s域分析及MATLAB实现
张登奇1, 张 璇2
(1. 湖南理工学院 信息与通信工程学院, 湖南 岳阳 414006; 2. 湖南大学 信息科学与工程学院, 长沙 410082)
微分方程是描述连续时间系统的数学模型, 求解响应是系统分析的重要内容. 直接求解微分方程概念清楚、方法直观但计算量大, 利用拉普拉斯变换间接求解微分方程是求解响应的有效方法. 文章以拉普拉斯变换为基础, 介绍了s域分析连续时间系统的原理和方法, 列举了MATLAB实现的程序.
连续时间系统; 拉普拉斯变换;s域分析; MATLAB
引言
微分方程是描述线性时不变连续时间系统的数学模型, 求解响应是分析连续时间系统的重要内容.直接求解微分方程的齐次解和特解是经典的求解方法, 求得的齐次解与自由响应对应, 特解与强迫响应对应. 经典法求解微分方程概念清楚、方法直观、便于理解, 但初始条件的计算和求解高阶微分方程都非常麻烦. 以拉氏变换为数学工具, 把系统输入的时域信号和描述系统的微分方程进行变换, 在s域求解系统响应的象函数, 再将象函数逆变成响应原函数, 这种s域分析方法将时域微分方程简化成s域代数方程求解, 且无需计算初始条件, 是分析连续时间系统的有效方法. 该方法也适于计算物理意义明显的零输入响应和零状态响应, 或瞬态响应和稳态响应. 本文以拉氏变换为基础, 介绍连续时间系统的s域分析原理,分析各种响应象函数的特点, 总结连续时间系统的s域分析方法, 用实例说明s域分析系统响应的步骤,并列举出MATLAB实现的程序.
1 拉普拉斯变换
拉普拉斯变换是s域分析连续时间系统的数学工具. 如果响应只计算某时刻以后的系统输出, 则可令该时刻为时间起点, 将运算繁杂且收敛域必须时时考虑的双边拉氏变换简化成单边拉氏变换进行计算.单边拉氏变换的积分时间起点是从零开始的, 积分结果与时的函数值无关, 逆变换当然只能给出时间段的函数值. 实际问题一般只需计算某一时刻以后的系统输出, 如果将该时刻定义为时间起点,拉氏逆变换的这种时间局限性并未给其应用带来不便. 关于积分时间起点的选定问题, 一般把时间起点记为0时刻, 其前瞬间记为时刻, 其后瞬间记为时刻, 考虑到积分下限取0时刻点时某些函数(如冲激函数)的积分值不能确定, 单边拉氏变换的积分下限应避开0时刻点. 选时刻作积分下限是可行的[1], 积分函数的状态往往需重新计算. 若选时刻作积分下限, 由于积分函数的状态一般已知, 可省去状态计算, 所以单边拉氏变换的积分下限都选时刻. 通常所说的拉氏变换都是指积分下限为的单边拉氏变换, MATLAB中的laplace积分函数也是如此. 拉氏变换的线性和时域微分定理是s域分析连续时间系统常用的重要性质, 这里只列出时的时域微分定理公式

2 连续时间系统的s域分析
连续时间系统的s域分析, 是以拉氏变换为数学工具, 先将时域微分方程变换成s域代数方程, 再在s域求解响应的象函数, 最后将响应象函数逆变换成时域原函数, 是一种间接求解系统响应的分析方法[2,3].设描述系统的微分方程一般式为

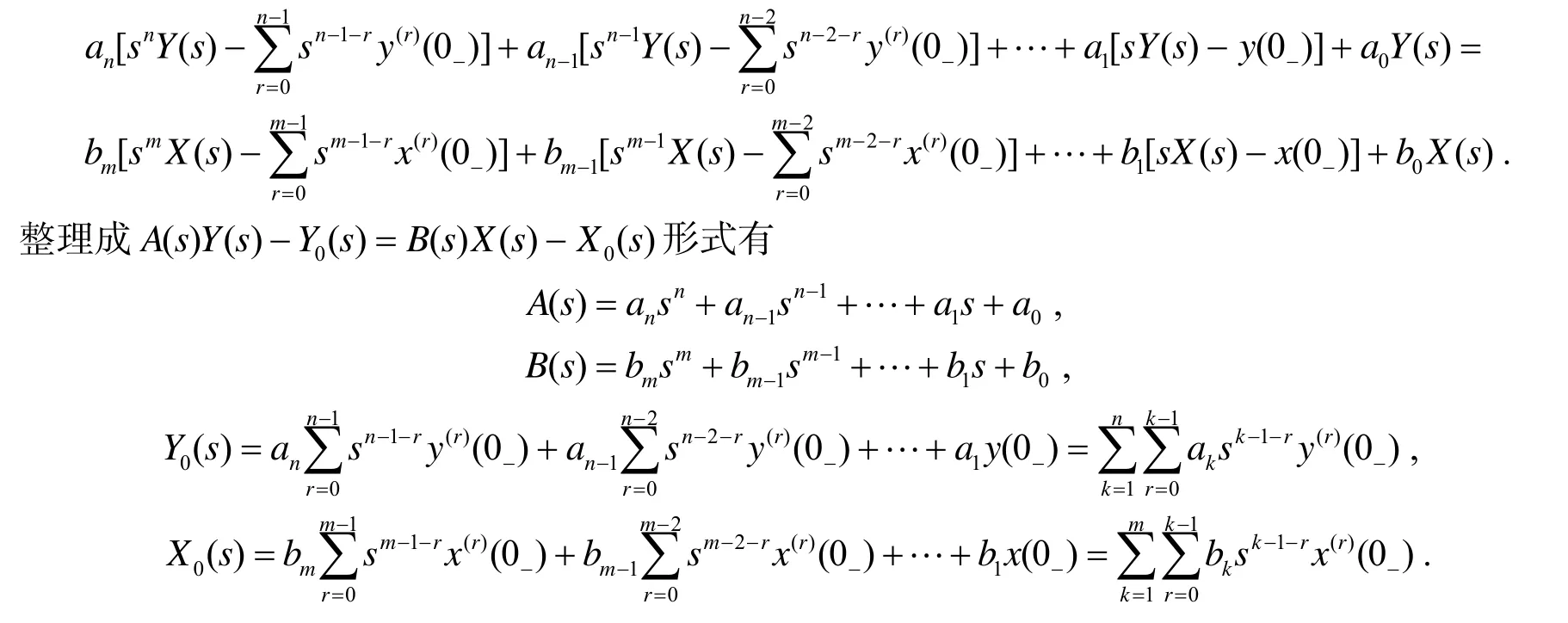

2.1 各种响应的s域求解分析
(1) 自由响应: 定义为微分方程的齐次解. 根据经典法可知它与系统函数的极点有关, 将进行逆变换时与系统函数的极点对应的那部分响应就是自由响应.
(2) 强迫响应: 定义为微分方程的特解. 根据经典法可知它与激励有关, 由的极点决定, 将进行逆变换时与的极点对应的那部分响应就是强迫响应.
(3) 瞬态响应: 定义为随时间增长而趋于零的响应. 即的极点中分布在s平面左半部分的极点对应的响应.
(4) 稳态响应: 定义为随时间增长而不消失的响应. 即的极点中分布在虚轴或s平面右半部分的极点对应的响应.
(5) 零输入响应: 定义为没有外加激励信号, 只由系统的起始状态所产生的响应. 即表达式中均为零时的拉氏逆变换. 这里解释一下为什么也要为零. 假设激励信号的起始状态(激励信号及其各阶导数在时刻的值)不都为零, 在0时刻跳变, 在0时刻以后都为零. 因激励信号或其各阶导数在0时刻点有跳变, 跳变值有不同的定义[5], 跳变值本身就存在不确定性. 如果微分方程右边还存在该跳变求导, 则在0时刻点方程右边出现冲激, 微分方程右边一定不为零. 零输入响应的定义要求微分方程右边在0时刻点也要为零, 故在计算零输入响应时激励信号的起始状态应为零, 至少也要保证微分方程右边不出现冲激.
(6) 零状态响应: 定义为系统的起始状态为零, 由外加激励所产生的响应. 即表达式中为零时的拉氏逆变换.
2.2 各种响应的s域求解步骤
已知系统的微分方程和激励信号, 根据系统的起始状态, 利用拉氏变换在s域求解系统响应的步骤可归纳如下:
(4) 在s域求解代数方程得响应象函数的逆变换即为系统响应;
(5) 分析响应象函数的极点来源及在s平面中的位置, 确定自由响应和强迫响应, 或瞬态响应和稳态响应;
(6) 根据零输入响应和零状态响应的定义, 在s域求解双零响应的象函数;
(7) 对双零响应的象函数进行拉氏逆变换, 得系统的零输入响应和零状态响应.
3 应用举例

下面介绍利用拉氏变换在s域分析系统响应的计算步骤.
对s域代数方程求解, 得系统响应的象函数
其中与系统函数的极点对应的是自由响应. 与激励象函数的极点对应的是强迫响应.的极点都在s平面的左半平面故都是瞬态响应. 零输入响应和零状态响应可按定义参照求解.
上述分析求解过程可借助MATLAB的符号运算编程实现. 实现s域分析的m程序如下:
clc;close all;clear;format compact;
syms s t %定义符号对象
%给出激励信号、微分方程和起始状态
xt=2*exp(-4*t)*heaviside(t), %激励信号, 冲激信号直接用dirac(t)
a=[1, 6, 11, 6], b=[1, 7, 8], %微分方程系数向量
y0=[1, 13, -61], x0=[-1, -2], %起始状态, y0的数据个数比a少1, x0比b少1
As=poly2sym(a, 's'), Bs=poly2sym(b, 's'), %计算As和Bs
Hsp=roots(a);disp('系统极点: '), Hsp, %计算系统极点并显示
Xs=laplace(xt), %对激励信号进行拉氏变换
%求Y0s, 注意系数标号与变量下标的关系
n=length(a)-1;Y0s=0;
for k=1:n;
for r=0:(k-1);Y0s = Y0s+a(n-k+1)*y0(r+1)*s^(k-1-r); end
end
Y0s, %显示Y0s符号多项式
%求X0s, 注意系数标号与变量下标的关系
m=length(b)-1;X0s=0;
for k=1:m;
for r=0:(k-1);X0s = X0s+b(m-k+1)*x0(r+1)*s^(k-1-r); end
end
X0s, %显示X0s符号多项式
%输出计算结果
Hs=Bs/As;disp('H(s)='), pretty(Hs), %显示系统函数便读式
ht=ilaplace(Hs);disp('系统冲激响应: '), ht, %计算并显示冲激响应
Ys=(Bs*Xs-X0s+Y0s)/As;disp('Y(s)='), pretty(Ys), %显示响应象函数
yt=ilaplace(Ys);disp('系统全响应: '), yt, %计算并显示全响应
yzit0=ilaplace(Y0s/As);yzit=vpa(yzit0, 4);%求零输入响应
disp('零输入响应: '), yzit, %输出零输入响应
yzst0=ilaplace((Bs*Xs-X0s)/As);yzst=vpa(yzst0, 4);%求零状态响应
disp('零状态响应: '), yzst, %输出零状态响应
%输出结果图示程序
t1=linspace(eps, 5, 100);%在0+到5秒取100个时点
ht1=subs(ht, t, t1);%利用置换函数求冲激响应各时点的数值解
subplot(2, 1, 1);plot(t1, ht1), %绘冲激响应
xlabel('时间(秒)'), ylabel('幅度'), grid, title('冲激响应'), %加标签
yt1=subs(yt, t, t1);subplot(2, 1, 2);plot(t1, yt1, 'r-'), %绘全响应
yzit1=subs(yzit, t, t1);hold on;plot(t1, yzit1, 'g:'), %同窗绘零输入响应
yzst1=subs(yzst, t, t1);hold on;plot(t1, yzst1, 'b-. '), %同窗绘零状态响应
legend('全响应', '零输入', '零状态', 0), %加响应图例, 位置自动最佳
xlabel('时间(秒)'), ylabel('幅度'), grid, title('系统响应'), %加标签
实例列出了求解系统响应的手算步骤和机算程序, 程序运行结果略. 值得一提的是利用ilaplace函数算出的时域解析式可能还要进行手工整理.
4 结束语
通过拉氏变换间接求解系统响应的s域分析方法, 较直接求解微分方程的经典法而言, 其概念抽象但运算简单. 本文通过对s域分析的原理介绍和应用举例, 介绍了系统响应象函数的极点与各类响应的对应关系, 澄清了零输入响应和零状态响应的模糊认识, 列出的s域分析程序对教学科研也有一定的应用价值.
[1] 郑君里, 应启珩, 杨为理. 信号与系统[M]. 第2版. 北京: 高等教育出版社, 2000: 180
[2] 吴大正, 杨林耀, 张永瑞. 信号与线性系统分析[M]. 第3版. 北京: 高等教育出版社, 1998: 234
[3] 朱 煜, 赵乐军. 信号与系统分析[M]. 北京: 机械工业出版社, 2005: 192
[4] 岳振军, 贾永兴, 余远德, 等. 信号与系统[M]. 北京: 机械工业出版社, 2008: 164
[5] Charles L. Phillips, Johe M. Parr, Eve A. Riskin. 信号、系统和变换[M]. 第4版. 陈从颜, 等, 译. 北京: 机械工业出版社, 2009: 32
[6] 张登奇, 张 璇. 冲激函数匹配法在初始条件计算中的应用[J]. 湖南理工学院学报(自然科学版), 2011, 24(3): 31~34
[7] 吴湘淇. 信号、系统与信号处理(上)[M]. 北京: 电子工业出版社, 2000
[8] 张志勇. 精通MATLAB6. 5[M]. 北京: 北京航空航天大学出版社, 2003
Analysis of Continuous-time System in s-domain and Realization Based on MATLAB
ZHANG Deng-qi1, ZHANG Xuan2
(1. College of Information and Communication Engineering, Hunan Institute of Science and Technology, Yueyang 414006, China; 2. College of Information Science & Engineering, Hunan University, Changsha 410082, China)
Differential equation is a mathematical model to describe the continuous-time systems, solving response is an important content for the system analysis. Direct method for solving differential equations has clear concept, intuitive method but large computation. Using the Laplace transform to solve the differential equation indirectly is an effective way for solving the response. According to the Laplace transform theory, this paper introduces the principles and the methods of analysis Continuous-time System in s-domain, also gives the programs based on MATLAB.
continuous-time system; Laplace transform; s-domain analysis; MATLAB
TP271. 6; TP391. 75
A
1672-5298(2012)02-0026-04
2012-03-20
张登奇(1968- ), 男, 湖南临湘人, 硕士, 湖南理工学院信息与通信工程学院副教授. 主要研究方向: 信号与信息处理

