基于改进型不变分布阈值量化方法的直扩码设计及优选

王喜风，王可人，焦传海，田上成

(电子工程学院信息系，安徽 合肥 230037)

0 引言

军用和民用通信的快速发展对直接序列扩频通信提出了新的要求，民用上要求其能满足大量用户通信的需求，军用上要求其具有较高保密通信能力。混沌系统具有非线性、初值敏感性、复杂度高、相关性好等优点，可以产生满足以上要求的直扩(direct spectrum，DS)码。

利用混沌映射产生DS码的一般步骤是:构造混沌映射，对其产生的混沌实值序列进行量化，根据性能指标要求对量化后的混沌序列进行优选，得到满足设计要求的DS码。耦合映象格子(coupled map lattice，CML)由于计算效率高，时间和空间上均有混沌行为，具有更高的随机性和复杂性等优点，从而被用于DS码的产生［1］。

针对CML序列的量化问题，文献［2］提出了用有限精度的二进制数表示的量化方法，该方法生成数据速度快，序列相关性好，但受到系统有限字长的限制，存在被预测跟踪的安全问题。针对基于均值的阈值量化方法得到的CML序列性能较差的问题［3］，文献［4］提出了一种改进的时空混沌量化方法，但该方法实时性较差，生成序列速度较慢。为此，文献［5］针对单向耦合映象格子(one way coupled map lattice，OCML)提出了基于不变分布的阈值量化方法，该方法实时性较好，序列的自相关性与由文献［2］得到的序列的自相关性相当，同时平衡性有了很大的提高，但为了产生互相关性较好的序列，该方法牺牲了OCML映射的空间间隔，使得OCML映射的利用率非常低。另外，对混沌序列的优选一般是将序列的各项性能指标与优选门限进行比较，舍弃达不到要求的序列［6］，这种优选方法不适用于实时的DS码产生。

本文提出了一种基于Tent映射的双向耦合映象格子(double way coupled map lattice based on Tent map，TDCML)和改进型不变分布阈值量化方法相结合的DS码产生方法。改进的量化方法在不牺牲映射利用率的情况下，量化得到具有良好性能的TDCML序列。分析产生TDCML优选序列的最优映射参数和序列选取方式，通过预设最优映射参数和序列选取方式来实时产生DS码。最后对优选出的TDCML序列进行随机性测试和DS/CDMA系统误码率分析。仿真表明，本文得到的优选TDCML序列具有良好的性能，适合作为DS码。

1 改进型不变分布阈值量化方法

1.1 TDCML映射模型

TDCML映射的数学表达式为

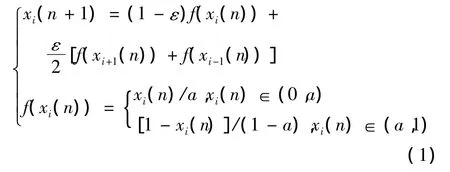
(1)式中:i为格点坐标，i=1，2，…，L;L为系统尺度;n为迭代次数;xi(n)为第i维格点第n次迭代后的状态值;f(xi(n))为xi(n)经Tent映射迭代后的格点状态值;ε为耦合系数，且0＜ε＜1;a为局部映射的分形参数，且0＜a＜1;边界条件为x0(n)=xL(n)，xL+1(n)=x1(n)。

经基于不变分布的阈值量化方法得到的OCML序列具有良好的自相关性和平衡性，但是互相关性较差，如果要用一个OCML映射产生多路DS码，OCML映射的利用率就很低。而DCML映射经基于不变分布的阈值量化方法得到的混沌序列具有良好的互相关性和平衡性，虽然自相关特性在一些延迟时间上有较大的峰值，但可以通过本文的量化方法解决这个问题，所以本文采用TDCML映射。

1.2 改进型不变分布阈值量化方法

由于TDCML序列的自相关函数在一些延迟时间上存在峰值，舍弃产生这些峰值的序列即可删除这些峰值，所以对TDCML实值序列进行一定间隔的抽取，再利用基于不变分布的阈值量化方法对实值序列进行量化，该量化方法称为改进型不变分布阈值量化方法。

改进型不变分布阈值量化方法的步骤如下。

步骤1 对L维的 TDCML实值序列 {xj，1，xj，2，…，xj，n}，j=1，…，L ，在时间方向上进行一定间隔p 的抽取得到 {xj，1，xj，1+p，…，xj，1+i·p}，j=1，…，L 。

步骤2 利用直方图法或区间迭代法［7］计算{xj，1，xj，1+p，…，xj，1+i·p}的不变分布，选取 xj，1+k·p作为阈值量化的判别基准，其中 0 ＜ k ＜ i，xj，1+k·p是所在序列的不变分布等于0.5时所对应的序列值。

步骤3 对抽取后的实值序列进行阈值量化sj，i=sgn{xj，1+i·p－ xj，1+k·p}，得到 TDCML 序列:{sj，1，sj，2，…，sj，i}。

在确定的参数控制下，DCML序列的不变分布是固定的，所以这个 xj，1+k·p可以预先求得，作为一个常数。另外，由于判别基准采用的是不变分布等于0.5 的序列值 xj，1+k·p，所以大于和小于判别基准的序列数目应相等，即 Num(x＞ xj，1+k·p)=Num(x ＜ xj，1+k·p)。

设抽取间隔 p=3，得到阈值 xj，1+k·p=0.525，通过改进型不变分布阈值量化方法得到的TDCML序列(TDCML-S)的自相关特性有了明显的改进，而利用文献［5］提出的基于不变分布的阈值量化方法得到的 TDCML序列(TDCML-S1)的自相关函数Rac(τ)在τ=±2，±2 046等地方有较大的峰值，τ为序列的延迟时间，一般无单位，如图1所示。

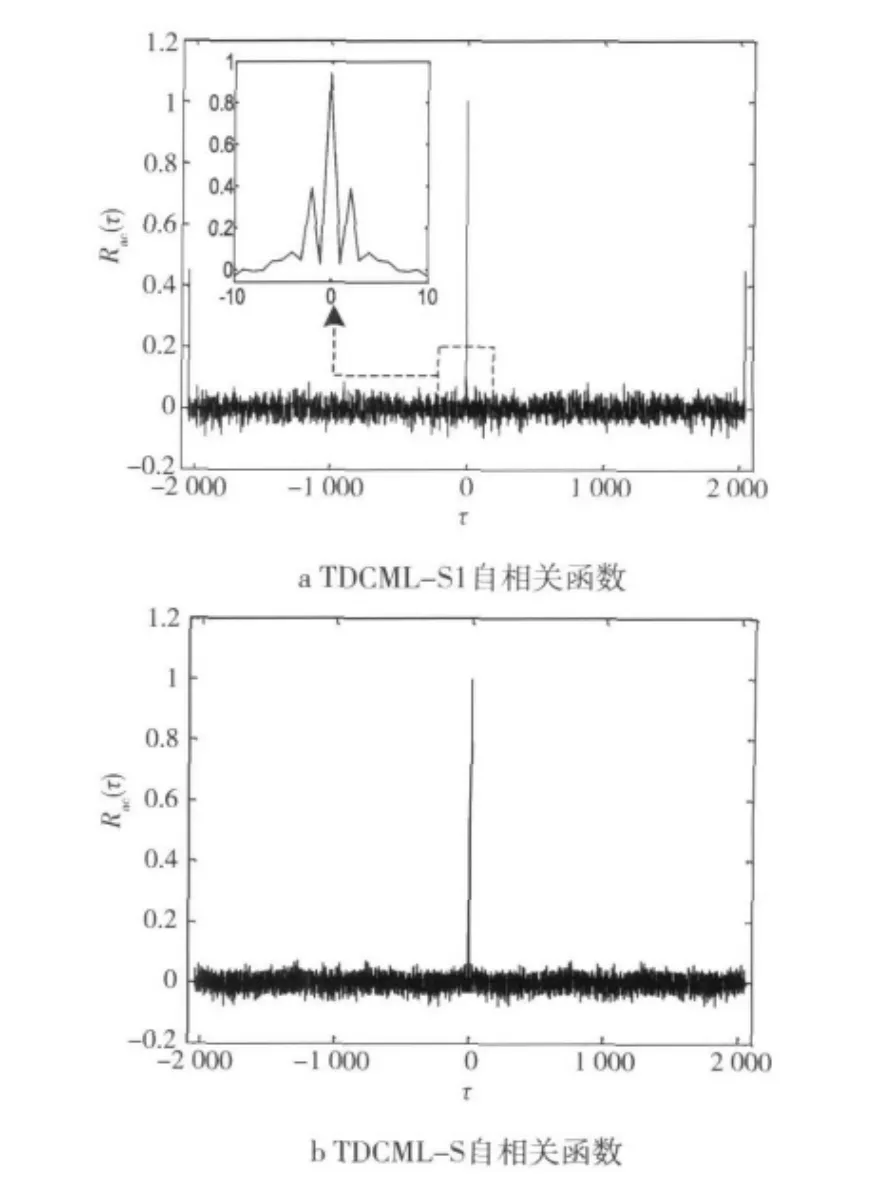
图1 TDCML-S1与TDCML-S自相关函数比较Fig.1 Comparison of self-correlation function between TDCML-S1 and TDCML-S

1.3 性能比较

对混沌序列进行性能分析，判断其是否可以作为DS码的主要性能指标有:平衡度H［8-9］、自相关抑制比 IDa［10］、自相关均方根 ΔRac［11］、互相关抑制比、互相关均方根。

由于经多比特量化得到的混沌序列具有良好的相关性［3］，所以将本文得到的序列的性能与经多比特量化得到的序列性能进行比较。TDCML-S和经多比特量化得到的TDCML序列(TDCML-S2)在不同序列长度下的性能比较如表1所示。与TDCMLS2比较，TDCML-S在其他性能不降低的情况下，平衡度得到了提高。

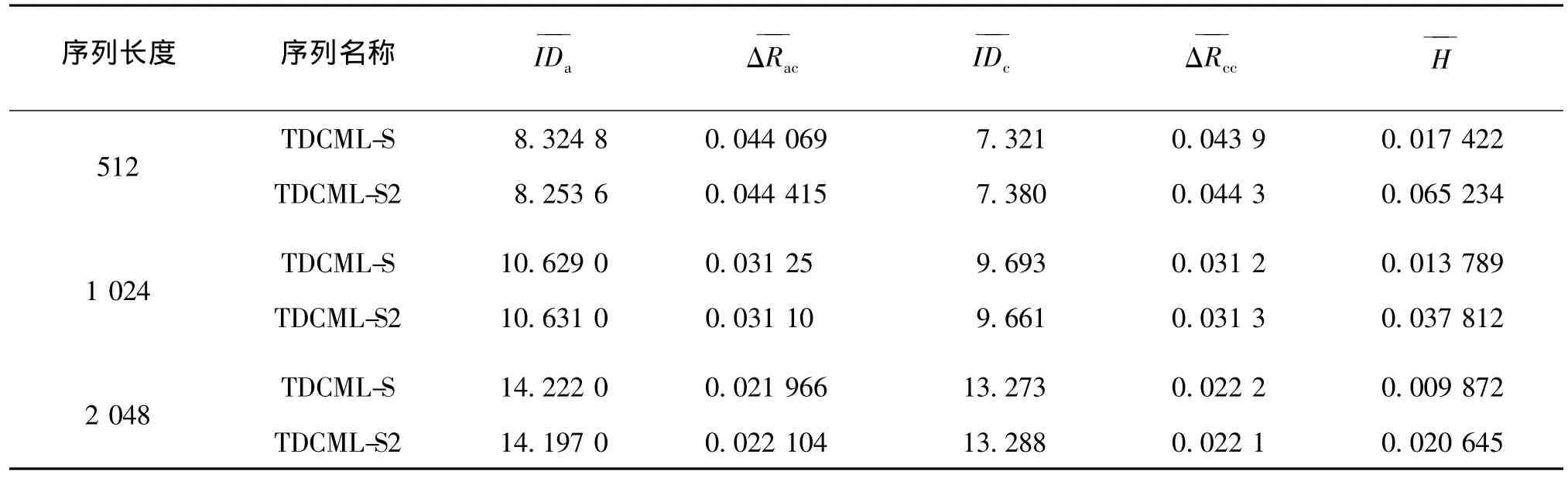
表1 TDCML-S与TDCML-S2在不同长度时的性能比较Tab.1 Property comparison between TDCML-S and TDCML-S2 for different lengths

当空间间隔Δi≥3时，TDCML-S的互相关性与TDCML-S2的互相关性相当，而OCML映射中的格点序列的互相关性要达到该指标，其空间间隔Δi≥20。

2 TDCML-S的性能分析

影响TDCML-S性能的主要因素有:1)映射参数的选取，包括耦合系数ε和分形参数a;2)TDCML-S的序列选取，包括空间间隔Δi和时间间隔Δn。

通过对TDCML-S进行性能分析，找到能产生性能更好的TDCML-S的最优映射参数和序列选取方式，从而优选出DS码。这种通过控制参数选择、序列选取方式的优选方法可以实时产生性能最好的DS码，有利于实际应用。

2.1 TDCML-S性能与空间间隔、时间间隔的关系

TDCML-S的序列选取可以在空间方向上选取，也可以在时间方向上选取或者在空间和时间方向上按照某种规则选取。下面研究空间间隔Δi、时间间隔Δn对TDCML-S性能的影响，序列长度取2 048 bit，维数L=128。通过Tent映射，以每100次迭代选取一个数值的方式选取128个数值，作为驱动TDCML映射的各格点映射的初始值，减少了各格点初始值之间的相关性，另外只需一个Tent映射的初始值就可以驱动整个系统运行，易于系统控制。

2.1.1 时间间隔Δn与自相关性的关系

取ε=0.99，a=0.5，TDCML-S的自相关性与时间间隔Δn的关系如图2，可以看到，为得到具有较大IDa和较小 ΔRac的TDCML-S，要求 Δn≠1，2，4，同时考虑到TDCML的利用率问题，时间间隔Δn取3，5 或6。

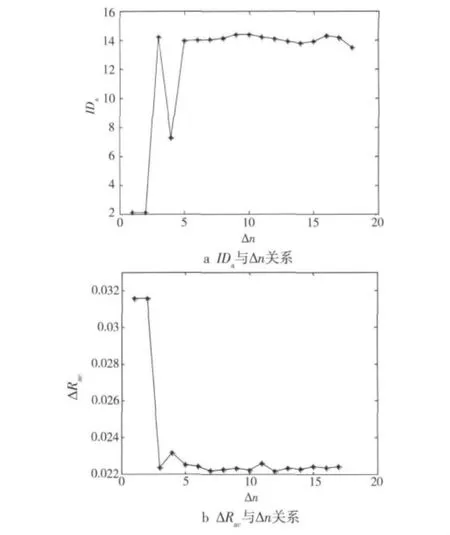
图2 时间间隔Δn与TDCML-S自相关性关系Fig.2 Relation between Δn and self-correlation of TDCML-S

2.1.2 空间间隔Δi与互相关性的关系

取ε=0.99，a=0.5，TDCML-S的互相关性与空间间隔Δi的关系如图3所示。可以看到，ΔRcc基本上不随Δi变化，但是IDc在Δi≤2时数值较小，Δi≥3时数值较大且较稳定，所以为了得到互相关性较好的TDCML-S，要求空间间隔Δi≥3。

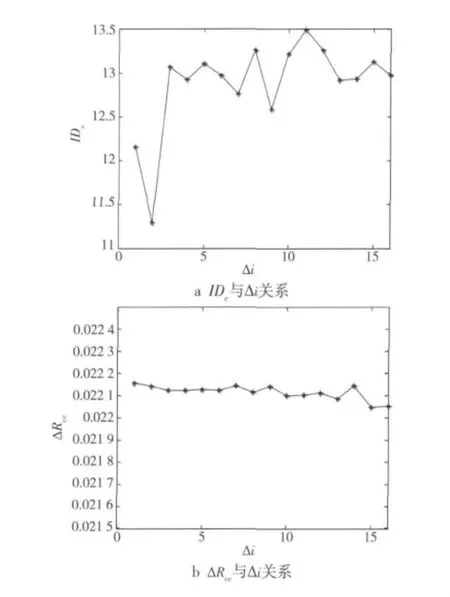
图3 空间间隔Δi与TDCML-S互相关性关系Fig.3 Relation between Δi and inter-correlation of TDCML-S

2.2 TDCML-S性能与耦合系数ε的关系

2.2.1 耦合系数ε与自相关特性的关系

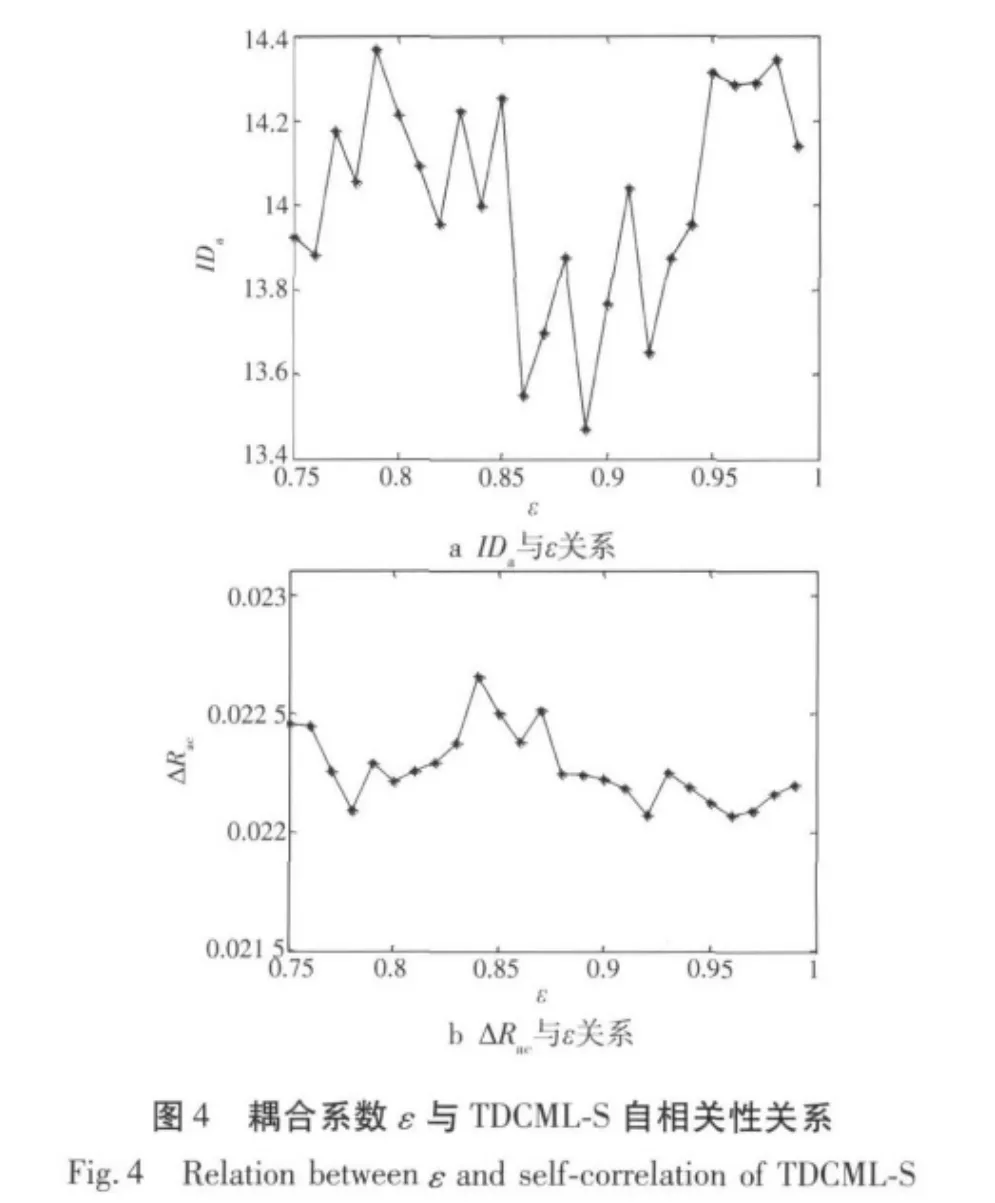
以时间间隔Δn=3的方式选取一组TDCML-S，该序列的自相关性与耦合系数ε的关系如图4所示。考虑当 ε∈ (0.75，1)［4］时易于收发系统同步，所以为了得到具有较大IDa和较小ΔRac的TDCML-S，要求ε≥0.96。

2.2.2 耦合系数ε与互相关特性的关系

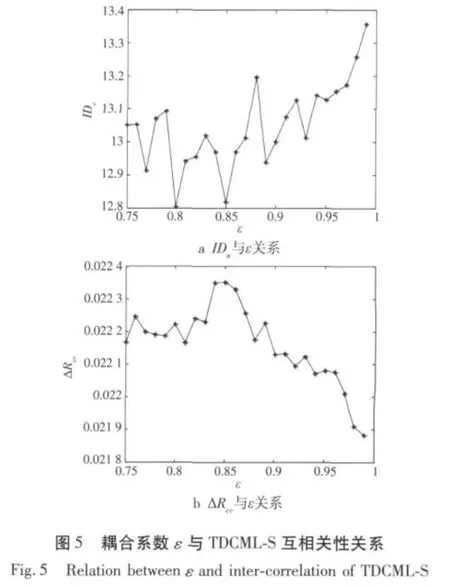
以时间间隔Δn=3，空间间隔Δi=3的方式选取一组TDCML-S，则该序列的互相关性与耦合系数ε的关系如图5所示。由于ε∈(0.75，1)，所以当ε≥0.95时，可以得到较大IDc和较小ΔRcc的TDCML-S。

2.3 TDCML-S性能与分形参数a的关系

2.3.1 分形参数a与自相关特性的关系

以时间间隔Δn=3的方式选取一组TDCML-S，该序列的自相关性与分形参数a的关系如图6所示。为得到较大IDa和较小ΔRac的TDCML-S，要求a取0.5左右。

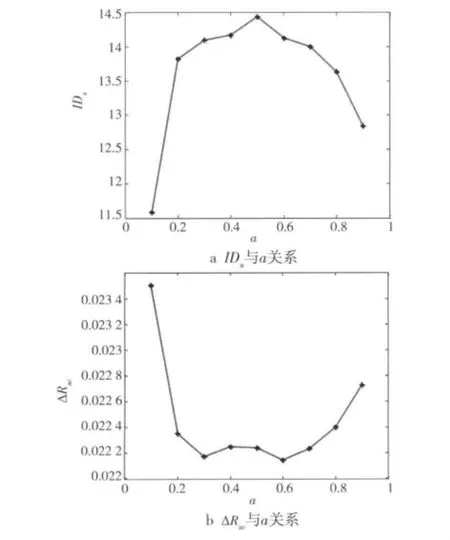
图6 分形参数a与TDCML-S自相关特性关系Fig.6 Relation between a and self-correlation of TDCML-S

2.3.2 分形参数a与互相关特性的关系

以时间间隔Δn=3，空间间隔Δi=3的方式选取一组TDCML-S，则该序列的互相关性与分形参数a的关系如图7所示。可以看到，当a取0.5左右时，可以得到较大IDc和较小ΔRcc的TDCML-S。

2.4 TDCML优选序列的性能

根据以上分析，综合考虑序列性能和利用率，选取 ε =0.995，a=0.5，L=128，Δn=5，Δi=5，得到一组TDCML优选序列，其性能如表2所示。与低维混沌映射相比，TDCML对初值更具敏感性，上述通过设置最优参数和序列选取方式的优选方法虽然减小了映射的可选取范围，但由于TDCML映射具有多个参数，且最优映射参数和序列选取方式的选取范围较宽，还是可以实时产生数量众多的优选序列。

表2 TDCML优选序列在不同长度时的性能Tab.2 Properties of TDCML optimized serials for different lengths

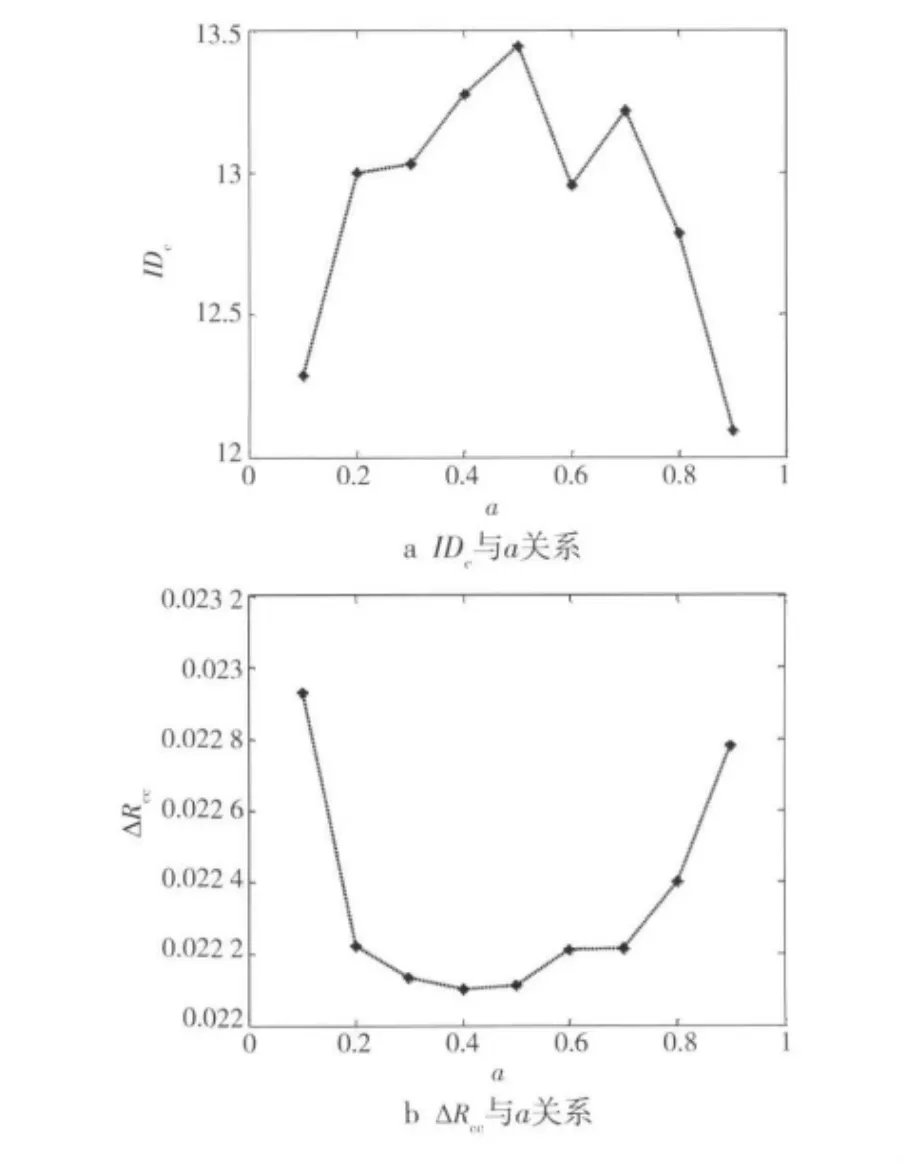
图7 分形参数a与TDCML-S互相关性关系Fig.7 Relation between a and inter-correlation of TDCML-S

3 TDCML优选序列的随机性测试和误码率分析

为测试优选序列的随机性和保密性，需对TDCML优选序列进行随机性测试，并讨论优选序列在DS/CDMA系统中的性能。

3.1 优选序列的随机性测试

优选序列的随机性测试标准主要采用美国国家标准和技术局(NIST)发布的SP 800-22测试标准，其测试项目见表3所示。

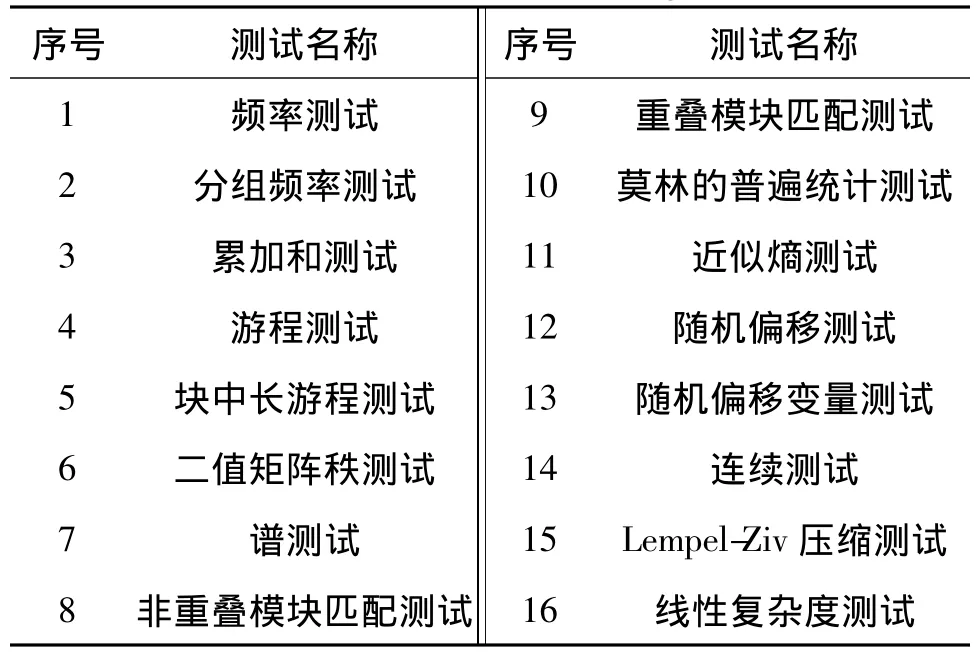
表3 NIST SP800-22测试项目Tab.3 NIST SP800-22 testing items

每组序列测试长度为20 000 bit，共测试1 000组序列，置信度水平α=0.01，若通过测试的序列比重在区间［0.980 560，0.999 439 2］时，以(1－α)×100%的显著水平认为优选序列通过了该项测试，测试结果的概率分布如图8所示，即以99%的显著水平认为优选序列通过了16项随机性测试。lts

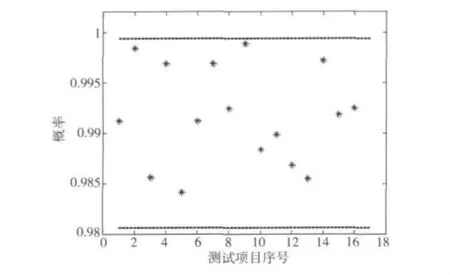
图8 16项测试结果概率分布图Fig.8 Probability distribution figure of the 16 testing resu

3.2 多用户DS/CDMA系统的误码率分析

将上面的TDCML优选序列作为DS码应用于多用户DS/CDMA系统中，进行误码率分析与比较。根据文献［12］，在同步接收时，加性高斯白噪声信道下DS/CDMA混沌扩频通信系统受多址干扰时的误码率公式为

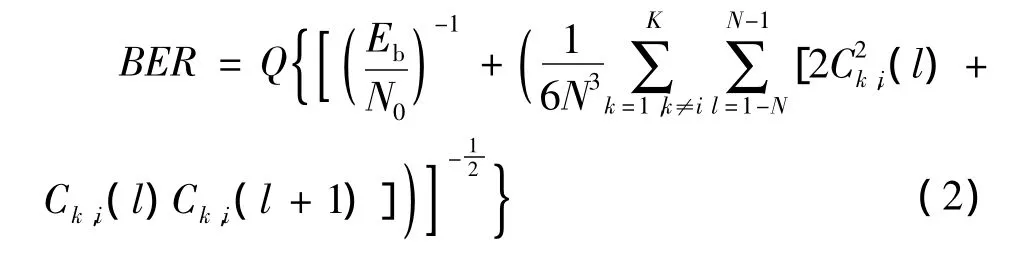
在多址干扰最小的情况下该系统的误码率最小，其理论值为［12］

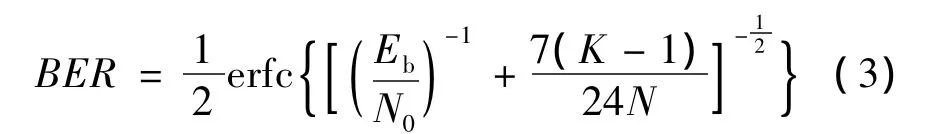
选取不同用户数 K=30，K=20，K=10，对TDCML优选序列进行DS/CDMA系统误码率分析，并与DS/CDMA系统误码率的理论最小值比较，如图9所示。可以看到，将TDCML优选序列作为DS码的DS/CDMA系统，经高斯白噪声信道和多径干扰后系统产生的误码率与理论最小值相当。

4 结论

改进型不变分布阈值量化方法得到的TDCML-S具有和由多比特量化方法得到的TDCML-S2一样的良好相关性能，同时平衡度得到了提高，且TDCML映射的利用率较高。通过对TDCML-S进行性能分析，确定产生最优序列的映射参数和序列选取方式，优选出DS码。与通过设定优选门限值的优选方法相比，本文优选方法能实时产生性能最优的DS码，有利于实际应用。对TDCML-S进行随机性测试和DS/CDMA系统误码率分析，表明优选出的序列具有良好的随机性，适合用于DS/CDMA通信系统。

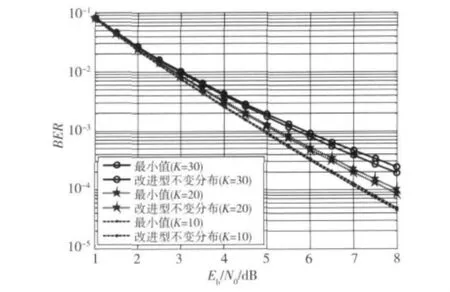
图9 混沌扩频系统误码率Fig.9 BER of chaotic spread spectrum communication system

［1］蔡觉平，李赞，宋文涛.一种混沌伪随机序列复杂度分析法［J］.物理学报，2003，52(8):1871-1875.CAI Jue-ping，LI Zan，SONG Wen-tao.Analysis on the chaotic pseudo-random sequence complexity［J］.Acta Physica Sinica，2003，52(8):1871-1875.

［2］曹骝，毛耀斌，刘文波，等.时空混沌伪随机比特发生器及其FPGA实现［J］.系统工程与电子技术，2008，30(9):1606-1610.CAO Liu，MAO Yao-bin，LIU Wen-bo，et al.Pseudo-random bit generator based on spatio-temporal chaos and its FPGA implementation［J］.Systems Engineering and Electronics，2008，30(9):1606-1610.

［3］LI Ping，LI Zhong，HALANG Wolfgang A，et al.A multiple pseudo random-bit generator based on a spatiotemporal chaotic map［J］.Physics Letter A，349(2006):467-473.

［4］李宁，山秀明，任勇，等.一种实用的时空混沌二值化方法［J］.系统工程与电子技术，2002，24(11):60-63.LI Ning，SHAN Xiu-ming，REN Yong，et al.A Practical Method to Transform Spatiotemporal Chaotic Sequences into Binary Sequences［J］.Systems Engineering and Electronics，2002，24(11):60-63.

［5］傅志坚，曾以成，徐茂林.基于单向耦合映象格子生成伪随机序列的两种新方法［J］.物理学报，2008，57(7):4014-4019.FU Zhi-jian，ZENG Yi-lin，XU Mao-lin.Two novel methods of generating pseudo random serials based on OCML［J］.Acta Physica Sinica，2008，57(7):4014-4019.

［6］余振超冯久超.一种混沌扩频序列的产生方法及其优选算法［J］.物理学报，2008，57(3):1409-1415.YU Zhen-ciao，FENG Jiu-chao.A method for generating chaotic spread-spectrum sequences and their optimized selection algorithm［J］.Acta Physica Sinica，2008，57(3):1409-1415.

［7］李辉，张锦刚，徐佩霞.求解混沌映射不变分布的区间迭代算法［J］.电路与系统学报，2003，8(2):6-9.LI Hui，ZHANG Jin-gang，XU Pei-xia.A domain iteration method for calculation of Invariant probability distribution for chaotic map［J］.Journal of circuits and systems，2003，8(2):6-9.

［8］李长庚，周家令，孙克辉，等.四种数字混沌扩频序列的平衡性分析［J］.计算机应用，2008，28(1):68-70.LI Chang-geng，ZHOU Jia-ling，SUN Ke-hui，et al.Balance analysis of four digital chaotic spread spectrum sequences［J］.Computer Application，2008，28(1):68-70.

［9］于银辉，刘卫东.两种混沌扩频序列平衡性分析［J］.重庆邮电大学学报:自然科学版，2004，16(3):61-64.YU Ying-hui，LIU Wei-dong.Analysis of balance of chaotic spreading spectrum sequences based on logistic-map and tent-map［J］.Journal of chongqing university of posts and telecommunications:Natural Science Edition，2004，16(3):61-64.

［10］金红，王可人，薛磊，等.一种用于CDMA系统的混沌多值数字序列及其性能［J］.电子学报，2000，28(4):131-134.JIN Hong，WANG Ke-ren，XUE Lei，et al.Chaotic multilevel digital sequence for the CDMA system and its properties［J］.Acta Electronic Sinica，2000，28(4):131-134.

［11］刘联会，石军，石磊.混沌扩频序列的优选算法及其系统性能研究［J］.系统工程与电子技术，2004，26(12):1909-1911.LIU Lian-hui，SHI Jun，SHI Lei.Optimization algorithm for chaotic spread-spectrum sequences and its system performance analysis［J］.Systems Engineering and Electronics，2004，26(12):1909-1911.

［12］付晓梅，曹宇，赵晶晶，等.基于优化混沌扩频序列的DS/CDMA 系统［J］.天津大学学报，2008，41(1):48-51.FU Xiao-mei，CAO Yu，ZHAO Jing-jing，et al.Improved DS/CDMA System Performance Based on Optimal Chaotic Sequences［J］.Journal of Tianjin University，2008，41(1):48-51.