龙凤山灌区水稻生育期降水量多时间尺度分析

徐淑琴，王云鹤，杨 旭，董丽丽

（1.东北农业大学水利与建筑学院，哈尔滨 150030；2.黑龙江大学水利电力学院，哈尔滨 150080）

龙凤山灌区位于黑龙江省五常市中东部，拉林河支流牤牛河中游的龙凤山水库以下两岸滩地和台地上。牤牛河干流总长201 km，流域面积5 300 km2。龙凤山灌区位于北半球寒温带季风气候区，大陆性气候明显，冬季漫长严寒，夏季短促，温热多雨，春季干旱多风，秋季天气晴朗且凉爽。龙凤山灌区是五常市的主要农业区，是国家的重要粮食生产基地和商品粮基地。灌区总面积4.09万hm2，耕地面积3.064万hm2，现有水田灌溉面积2.50万hm2全部为水田。因此，龙凤山灌区水稻生育期降水变化的多时间尺度分析，分析其降水变化规律，抵御自然灾害，合理利用和分配水库蓄水量及水资源的可持续发展具有重要意义[1-3]。

目前，针对龙凤山灌区的研究众多聚焦在管理、节水工程及渠道方面，大部分着重于管理及设计方面研究，对于水稻生育期降水量变化规律分析的研究涉及不多。本文采用Morlet小波分析方法对龙凤山灌区（1953～2010年）水稻生育期降水量进行分析，分析龙凤山灌区降水量的变化特征、旱涝分布结构、周期演变规律及其发展趋势。这有利于进一步提高了龙凤山中长期分析预报能力，以便为龙凤山灌区水资源可持续利用和合理的政策制定提供依据[4-7]。

1 研究地区和研究方法

1.1 研究地区概况

龙凤山灌区是以龙凤山水库为主要水源，龙凤山水库至牤牛河口的区间径流为辅助水源的大型灌区。地理坐标为东经126°40′～127°40′，北纬44°45′～45°15′。龙凤山灌区内农业生产水平较高，主要作物为水稻，其次为豆类和玉米，水稻种植面积占粮食作物面积的82%以上。所以水稻生育期的降水量对水稻生长的影响至关重要。

1.2 研究方法

20世纪80年代初由Morlet提出的具有时频多分辨功能的小波分析是一种可调时频窗的分析方法，小波分析能将交织在一起的不同频率成分组成的复杂时间序列分解成频率不相同的子序列，能很好地描述非平稳信号，成功解决了时频局部化问题，为更好分析水文时间序列变化特性奠定了基础，小波分析为水文系统多时间尺度分析研究提供了强有力的工具。因此本文采用小波分析理论对龙凤山灌区水稻生育期降水量序列进行多时间尺度分析，揭示降水的周期特征、突变点和变化趋势，为以后灌区的用水及分配提供一定的参考[8-9]。

1.2.1 资料的预处理

龙凤山灌区（1953～2010年）水稻生育期的降水资料由五常市水务局提供。为处理方便，在进行小波变换之前需要对降水量进行距平比率计算，对距平比率序列进行连续小波变换。距平比率的计算公式如下[10]：

式中，xj,i为第j年第i月的降水量（mm）；为第i月降水量的多年平均值（mm）；Rj,i为第j年第i月的降水量距平比率。

1.2.2 小波变换

对于给定的小波函数 ψ（t），水文时间序列f（t）∈L2（R）的连续小波变换为

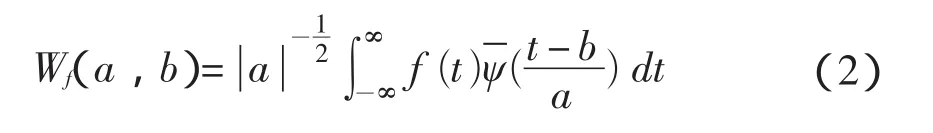
式中，a为尺度因子，反映小波的周期长度；b为时间因子，反映时间上的平移；Wf（a，b）称小波变换系数。实际工作中，时间序列常常是离散的，如 f（kΔt）（k=1，2，1，N；Δt为取样时间间隔），式（2）的离散形式为

式中，Wf（a，b）为小波系数；为 ψ（t）的复共轭函数。

W（fa，b）能同时反映时域参数b和频域参数a的特性，它是时间序列（ft）或（fkΔt）通过单位脉冲响应的滤波器的输出。

1.2.3 小波方差

将时间域上的关于a的所有小波变换系数的平方进行积分，即为小波方差：

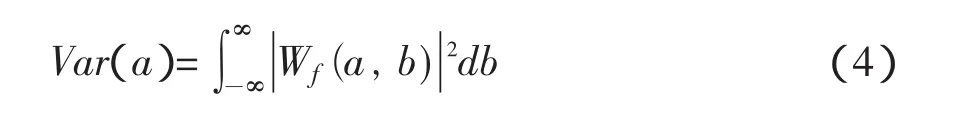
小波方差随尺度a的变化过程称为小波方差图。它反映了波动的能量随尺度的分布。通过小波方差图，可以确定一个水文序列中存在的主要时间尺度，即主周期。

2 龙凤山灌区水稻生育期降水量多时间尺度分析

将降水资料进行距平（中心化）处理，并绘制降水距平序列变化曲线，如图1所示。

基于上述方法绘制降水量距平序列小波变换系数Wf（a，b）的模平方分布（见图2）和实部分布（见图3），以此来分析水稻生育期降水距平的时频变化。

图2绘制了水稻生育期降水量距平序列小波变换模平方的时频变化。由图2可知，不同时段各时间尺度的强弱分布，其中4～7年时间尺度变化较强，主要发生在1977～1999年，振荡中心在1998年；12～17年时间尺度也十分强，主要发生在上个世纪60年代初至90年代初，振荡中心在1985年左右；其次1～3年时间尺度分别在1974～1980年、1994～2001年及2003～2010年期间出现明显；其余则较弱。

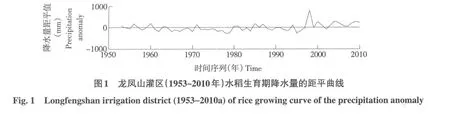
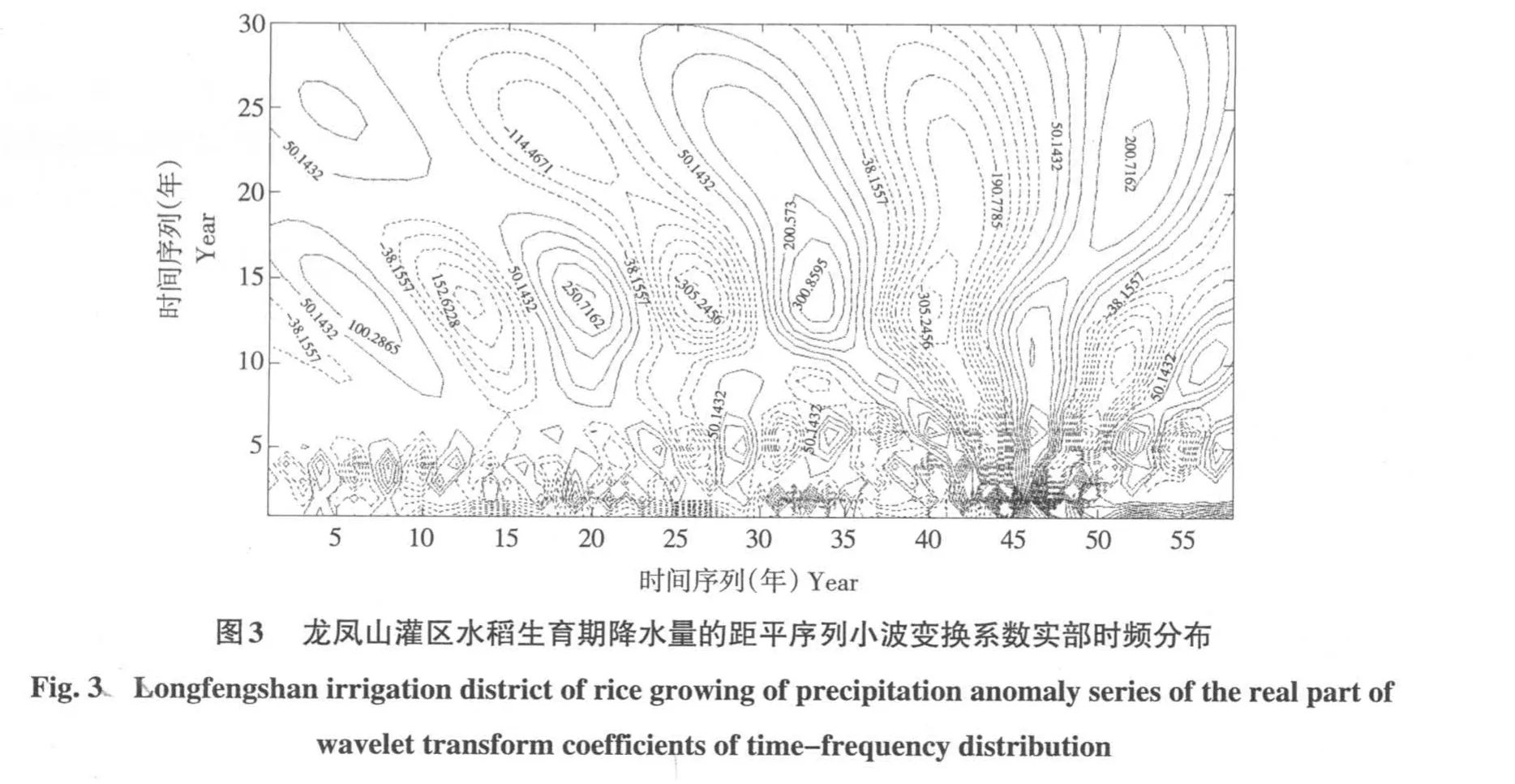
图3绘制了水稻生育期降水量距平序列小波变换实部的时频变化。图中清晰地显示了降水量时间尺度变化、突变特点分布及及其位相结构。其中4～7年尺度表现明显，其中心时间尺度为6年，正负相位交替出现；而12～28年时间尺度非常突出，其中心尺度在14年和24年。可以发现，14年尺度下 1954～1961 年、1968～1975 年、1982～1989年、1996～2001年及2006～2010年各时段为正位相，表示降水偏多；而1953年以前、1962～1967年、1976～1981年、1990～1995年及2002～2005年各时段为负位相，表示降水偏少；突变点在1954、1962、1968、1976、1982、1990、1996、2002 和2006年，小波系数在整个研究时域内主要经历了4次丰枯交替过程[11-13]。

由图4可以看出，小尺度下6和14年的小波系数，比较强，6年尺度下，未来两年将处于降水偏丰期，14年尺度下，未来7年内将处于降水偏丰期。而24年，稍弱，在2012年开始将处于降水偏少期。但无论是较大时间尺度，还是较小时间尺度，水稻生育期降水量均处于偏多期。所以，不同尺度下的丰枯交替不同，丰枯交替变化与时间尺度大小有紧密联系。

图5可以看出，生育期降水主要集中在6、14和24年主周期。

图4 龙凤山灌区水稻生育期降水量的距平序列不同时间尺度下的小波变换系数Fig.4 Longfengshan irrigation district of rice growing of precipitation anomaly series of different time scales of the wavelet transform coefficients

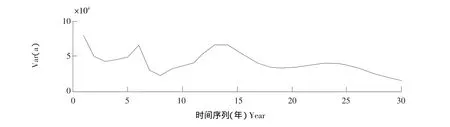
图5 龙凤山灌区水稻生育期降水量的距平序列的小波方差Fig.5 Longfengshan irrigation district of rice growing of precipitation anomaly series of wavelet variance

3 讨论与结论

通过Morlet小波分析可以发现，此方法对于未来趋势分析有较好的效果。但时间序列分析对数据要求较高，按照时间先后排列的数据越多越好，而现实中往往出于各种原因，不能有较多连续、精准数据，因此，模型建立及精度有限制性。

小波分析的时频局部化特性可展现水文时间序列的精细结构，为分析其多时间尺度变化特征提供了一种新途径。多时间尺度存在，使水文系统描述和分析难度加大[14-15]。小波分析为分析水文序列多时间尺度的变化提供科学指导，但处于在研讨和发展阶段，内容仍需完善，需要在应用中不断修改和提高。

本文采用Morlet小波分析的方法，对龙凤山灌区58年（1953～2010年）的水稻生育期降水量进行多时间尺度分析，研究结果如下：

a.龙凤山灌区水稻生育期降水量以长周期的上升趋势变化为主，大体经历了4次丰枯交替变换。从小尺度上看，丰枯交替较频繁[16]。从小波变换系数模平方和小波变换系数实部可以看出时间尺度的强弱和分布情况、变化趋势和突变点。

b.由小波方差分析发现，降水量变化具有6、14和24年主周期，且以14年周期最为显著。从中尺度来看，未来将处于降雨偏多期，从大尺度来看，2012年将处于降水偏少期。

c.影响降雨量因素很多，利用小波变换对降雨量序列分析方法还有提高的空间。今后，对降水量演变研究还有待于进一步加强。

[1]沃晓棠,黄智超.扎龙湿地近50年温度和降水年际变化分析[J].东北农业大学学报,2010,41(5):61-65.

[2]龚云,孔兰.南明河流域径流量时间序列演变趋势分析[J].中国农村水利水电,2011(1):14-18.

[3]崔锦泰.小波分析导论[M].西安:西安交通大学出版社,1995.

[4]李瑞平,史海滨,李彰俊.连续小波变换在气温和降水变换分析中的应用[J].灌溉排水学报,2008,27(1):86-89.

[5]王文圣,袁鹏,丁晶.小波分析及其在日流量过程随机模拟中的应用[J].水利学报,2002(11):43-48.

[6]杨磊磊,卢文喜,刘派.时间序列分析及Monte Carlo方法在降水预报中的应用[J].环境科学与技术,2011,34(5):108-112.

[7]丁红,王晓岩,刘东.852农场51a降水序列多时间尺度分析[J].黑龙江水专学报,2009,36(4):79-81.

[8]王文圣,李跃清.长江上游主要河流年径流序列变化特性分析[J].四川大学学报,2008,40(3):70-75.

[9]温忠辉,任化准,束龙仓.岩溶地下河日流量预测的小样本非线性时间序列模型[J].吉林大学学报,2011,41(2):455-464.

[10]王文圣,丁晶,李跃清.水文小波分析[M].北京:化学工业出版社,2005.

[11]方乐润,施鑫源.应用时间序列分析法模拟地下水资源系统[J].河海大学学报,1990,18(6):85-91.

[12]丁晶,王文圣.水文相似和尺度分析[J].水电能源科学,2004,22(1):1-4.

[13]文成林,周东华.多尺度估计理论[M].北京:清华大学出版社,2002.

[14]王文圣,丁晶,向红莲.水文时间序列多时间尺度分析的小波变换法[J].四川大学学报,2002,34(6):14-17.

[15]李贤彬,丁晶,李后强.水文时间序列的子波分析法[J].水科学进展,1999,10(2):144-149.

[16]李贤彬,丁晶,李后强.水文序列Hurst系数的子波估计法[J].水利学报,2000(2):6-9.