基于四端参数法的管路支架隔振性能研究
刘秀峰 王永胜 张京伟 吴崇健
1海军驻中国舰船研究设计中心军事代表室,湖北武汉430064 2中国舰船研究设计中心,湖北武汉430064
0 引 言
管路支架在船舶中俗称马脚,除了能起到支撑和固定管路的作用外,它还是管路与船体之间振动能量的传递中介。船舶上机械设备的振动和管内介质流动产生的脉动都会由管路经管路支架传递到船体上,因此,除了要控制振动在管路系统中的传递外,关于振动能量在管道与船体之间的隔离也是减振降噪研究的重要内容之一[1-2]。
随着船舶管路减振和隔振要求的不断提升,各种新型的隔振器和材料被运用到管路中[3-5],因此,对管路支架隔振性能的研究就显得尤为重要。蒋学武等[6]分析了管路橡胶减振器对刚性管路的隔振原理,但忽略了管道本身弹性和基础弹性的影响。朱石坚和Sciulli等[7-8]分别就基础弹性和被隔振物弹性对隔振系统传递率的影响进行了分析。本文将在考虑管道弹性和基础弹性的基础上,利用四端参数法[9]研究管路支架的隔振性能。
1 考虑管道弹性时的隔振分析
1.1 力学模型的建立
为了分析管道弹性对隔振效果的影响,首先要建立合适的力学模型。由于管道沿管长的尺寸要远大于截面尺寸,并且这里主要关心的是管道的弯曲振动,而不考虑横截面内发生的变形,因此,可以把管道看成是欧拉—伯努利梁。这根梁由多个管路支架支承,假设相邻支架间梁的长度为L/2,取长度为L的梁进行分析。先不考虑基础的弹性,即支架底部为固定约束,将支架用一个弹簧阻尼系统代替。这里只考虑垂向振动,忽略角刚度的影响,建立一个两端弹性支承的梁模型。假设梁中部受一个集中简谐激励力的作用,则整个结构可用如图1所示的隔振模型来表示。
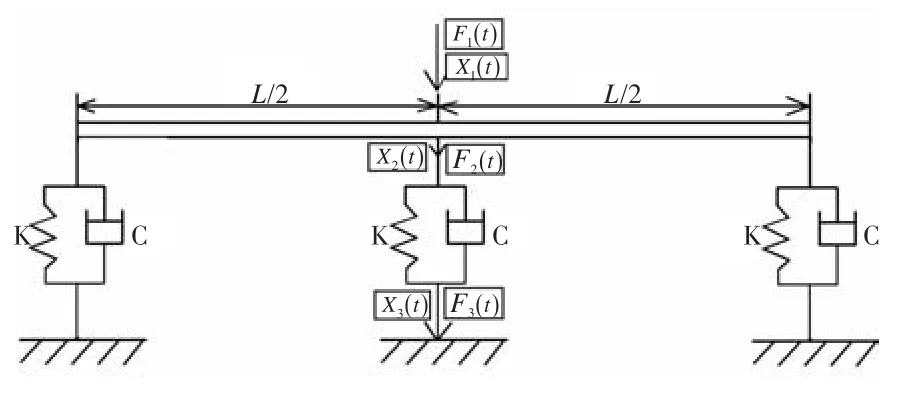
图1 考虑管道弹性时管路支架的隔振模型Fig.1 Vibration isolationmodelof piping support when considering elasticity of the pipeline
1.2 力传递率的推导
对图1所示的隔振系统模型,利用四端参数法求解传递率。由于基础是固定的,所以这里将主要考虑力的传递率μF。经过分析,可以得到等效的四端参数线路及其简化形式,如图2所示。

图2 考虑管道弹性时隔振系统的四端参数线路图Fig.2 Circuitdiagram of four-pole parametersof vibration isolation when considering elasticity of the pipeline
对于图2所示的线路图,有

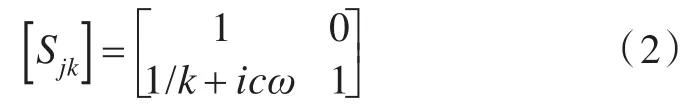
下面,再来考虑。假设在简支梁距端点ε处有一简谐激励力 F(t)=F0sinωt,假设为 F1,该力在梁中点A处引起的位移响应X1与F1之比为A点处的位移传递导纳M(A),并且 X1=X2,将这些力和位移的关系进行整理可写成如下矩阵形式:
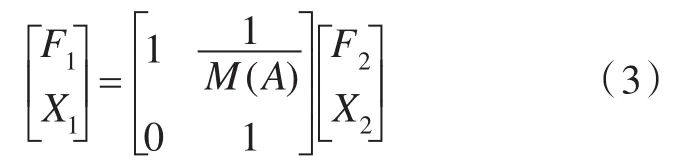
因此,,于是

由于基础固定,X3=0,得到力的传递率:
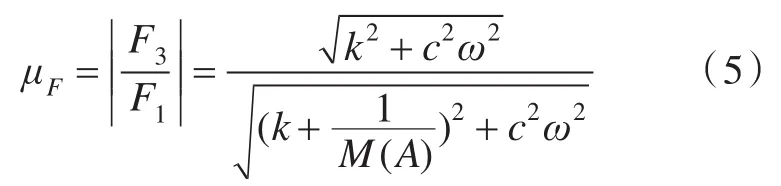
由式(5)可知,导纳 M(A)是问题的关键,而导纳决定于A点的位移响应。梁的位移响应一般由模态叠加法求得,因此,首先需要解决梁的模态振型函数,而目前还不能获得弹性支承梁振型函数的解析解。但有3种方法可以解决这一问题。方法1:由振动理论可知,梁的振动响应一般由低阶模态决定,高阶模态的影响较小,因此,可以利用数值方法求解出有限的前几阶模态解。不考虑阻尼时,弹性支承梁的频率方程为:

式中,EI为抗弯刚度;m为单位长度梁的质量;L为梁长;ωi是第i阶固有频率,可由数值法或图解法求得,然后代入梁的振型函数,并进行归一化,就可以得到弹性支承梁的前i阶正则振型。最后,利用叠加法求得导纳并代入式(5),便可获得传递率的近似解。
方法 2:Yang等[10]提出了一种将弹性支承梁的模态分离成简支弹性梁与弹性支承刚性梁的模态相叠加的方法,利用该方法,可以解得模态函数的近似解。但经过验证,这种方法获得的模态只有前两阶较为准确,可以用于低频计算,但在高频区域偏差较大。
方法3:由文献[11]可知,当弹性支承的刚度较大时,梁的模态频率与简支梁的频率差距非常小,因此,当支架刚度较大时,可以用简支梁的模型代替。由简支梁的弯曲振动理论,可以求得在简谐力作用下梁中点A处的位移导纳:

式中,ε为力作用点距梁左端的距离。梁的第i阶固有频率为:

将式(8)代入式(5),得

式(10)为简支梁模型时管路支架隔振系统力的传递率。当m与L确定时,μF是关于ωi,k,c,ω的函数,且传递率 μF越小,隔振效果便越好。
1.3 传递率曲线
为了形象地描述管道弹性对系统隔振效果的影响,选取一直径55mm、厚3 mm的管道作为研究对象,其各个参数为:E=2×1011Pa,σ=0.3,截面惯性矩 I=1.66×10-7m4,m=3.85 kg/m,管长L=4m,支架刚度k既可利用有限元软件根据文献[12]的方法进行受力分析得到,也可以由实验获得。选用两种较常见的支架进行计算,得到垂向刚度(取近似值)k1=5×105N/m和 k2=4×106N/m,并且令,其中 m′为广义质量,,取ε=L/2。利用这些参数和前面的公式,就可以得出考虑管道弹性时的力传递率曲线。下面,将从以下方面对其进行分析。
1)集中质量模型、简支梁模型和弹性支承梁模型力传递率的比较。不考虑管道弹性时将管道质量集中在一点,看成集中质量隔振系统,取一半管长的质量作为系统的集中质量,即m′=7.7 kg。当取阻尼比ζ=0.1,刚度选k1时,3种隔振模型的传递率曲线对比如图3所示。由图3可知,3种处理方式的结果区别较明显,考虑管道弹性时的传递率曲线存在多个峰值(峰值对应的频率并不直接等于梁的固有频率),这些峰值由管道固有振型被激发而引起,峰值的位置和数量与管道特性有关。另外,弹性支承梁模型与简支梁模型曲线也有区别,前者峰值靠前,特别是在高频区域,这种差别更大。因此,在对管路支架进行隔振分析时不能忽视管道弹性的影响,需选择合适的隔振模型。
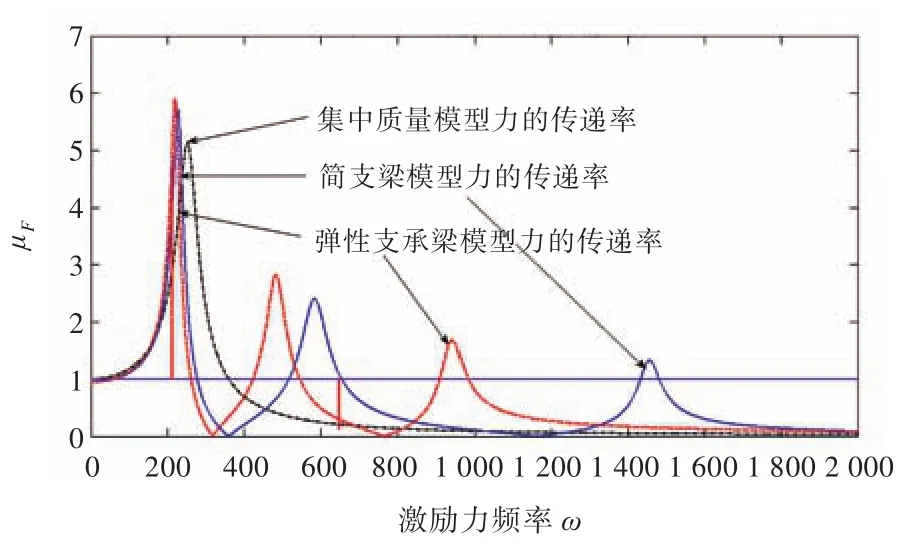
图3 3种隔振系统力的传递率曲线(k=5×105)Fig.3 Curvesof transfer rate of force for three kinds of vibration isolationmodels(k=5 ×105)
2)管路支架的刚度对弹性支承梁隔振系统力传递率曲线的影响。前面的分析是以管路支架的垂向刚度k1=5×105N/m为前提,现改变管路支架刚度,以k2=4×106N/m作为比较,其他条件相同,将2种情况下的μF变化曲线列于图4。
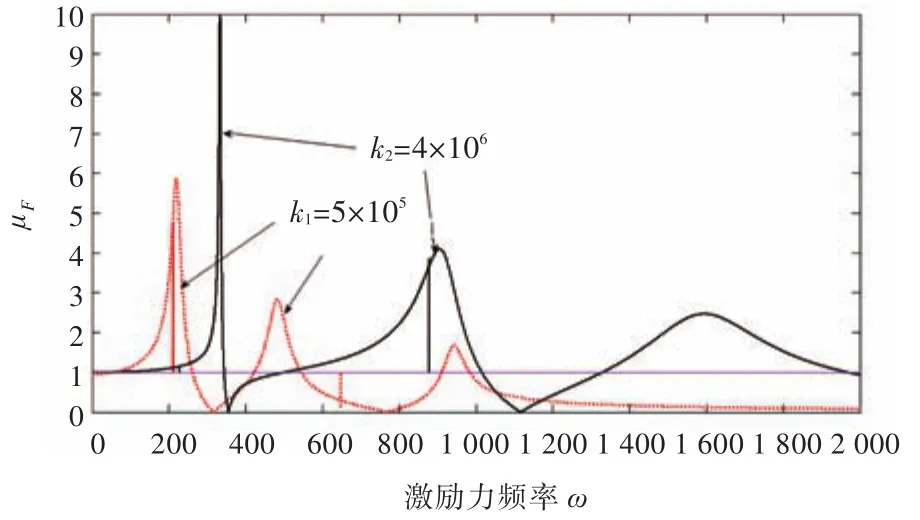
图4 支架刚度k对力传递率的影响Fig.4 Influence of the stiffnessof piping supporton transfer rate of force
对比图4中两条曲线可以看出:刚度k小的曲线各阶峰值要小于刚度大的曲线峰值,且位置靠前,衰减更快;刚度小的曲线在高频区域内要低于刚度大的曲线,但在低频区域(ω<300 rad/s),刚度小的曲线要高于刚度大的曲线。由此可见,刚度k是影响支架隔振性能的一个重要因素,但并非k越小隔振性能就越好,在低频区域,刚度k小的支架反而不利于隔振。
3)激励力作用位置对传递率曲线的影响。前面都是以力作用在梁中点为前提,现改变力的作用位置,假设激励力作用在L/4处,两种不同刚度k的支架的力传递率曲线对比如图5所示。
对比图5与图4可知,当激励力作用在L/4处时,曲线的峰值位置发生了变化,特别是第1和第2个主峰值由于位置靠近而融合在了一起,使得在低频内不隔振的区域扩大,这种变化对于刚度小的曲线更为明显。这说明力的作用位置对支架的隔振性能也有较大影响。
4)阻尼对力传递率曲线的影响。将阻尼比ζ减小到0.02,与前面相应曲线的比较如图6所示。

图5 激励力作用在L/4处时支架刚度对力传递率的影响Fig.5 Influence of the stiffness ofpiping supporton transfer rate of forcewhen the forcewasapplied to the L/4 ofbeam
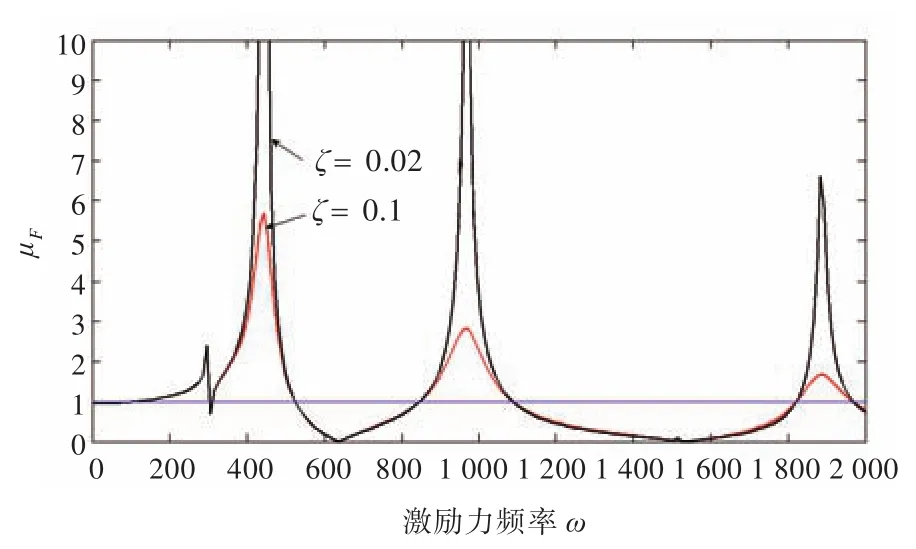
图6 阻尼对力传递率曲线的影响Fig.6 Influence of the damping of piping supporton transfer rate of force
图6 说明阻尼主要是降低曲线的峰值,对共振区域抑制作用较明显,对其他频域影响较小。
5)对管长L和支架刚度k隔振优化的近似计算。对于实际的一段管路,从支架隔振优化的角度来考虑怎样选择合适的支架安装间距和支架刚度是工程关心的问题。首先考虑管长L的选择,由于弹性支撑梁的模态解析解较难获得,当一般管路支架的垂向刚度较大时,可以用简支梁模型近似代替。图7列出了k2=4×106时两种模型力传递率的对比。由图可知,在支架刚度较大时,两种模型的曲线几乎一致。此时,可以利用公式(10)得到管长 L、激励频率ω与力传递率的关系,如图8所示。从其中选出2种激励频率(200,400 rad/s),L与力传递率的关系如图9所示。

图8 k2=4×106时L,ω与力传递率的关系Fig.8 The relationship between L,ω and transfer rate of forcewhen k2=4×106
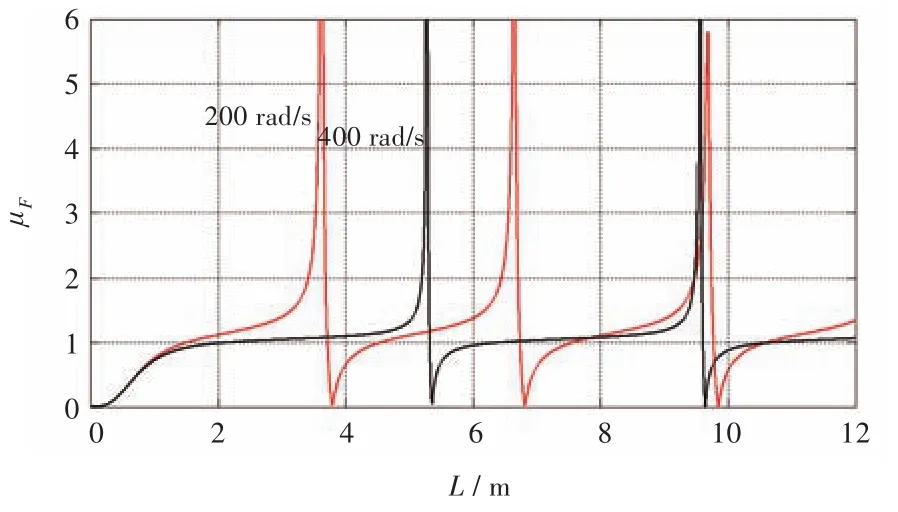
图9 ω=200,400 rad/s时L与力传递率的关系Fig.9 The relationship between L and transfer rate of forcewhen ω=200,400 rad/s
由图8和图9可知,对于给定的管路和管路支架,应首先根据管路激励频率ω选择合适的支架间距L/2,以避开共振区域,然后再适当调整达到最佳隔振效果。
其次,对于支架间距,当船舶安装环境已经被限定时,也可通过选择合适的刚度来提高支架隔振效果。由前面的分析可知,对于高频激励,刚度k越小,隔振效果便越好,但在低频频域,由于共振作用明显,刚度小的支架隔振效果反而更差。因刚度k在实际中的可选范围较大(相差可达十几倍),若用简支梁模型分析,对于低刚度支架会出现较大偏差。此时,可以利用方法2取前几阶模态获得传递率的解析式,并据此了解刚度k在低频时与传递率的关系,如图10所示。由该图可知,在已知激励频率时,可选择合适的k以避开共振而提高支架隔振效果。

图10 ω=200,300,400 rad/s时k与 μF的关系(L=4m)Fig.10 The relationship between k and transfer rate of force when ω =200,300,400 rad/s(L=4m)
2 基础弹性对隔振效果的影响
在船舶实际环境中,管路支架一般固定在船体上,这样的基础是具有弹性的,特别是当支架固定在较薄的船体板上时,基础的弹性变形就不能忽略。此时,管路支架基础的位移X3就不再为0。
2.1 传递率的推导
为研究基础弹性对支架隔振效果的影响,先绘出系统的等效四端参数线路图及其简化形式(图11)。

图11 考虑基础弹性时的四端参数线路图Fig.11 Circuit diagram of four-pole parametersof vibration isolation when considering elasticity of infrastructure
此时,由于基础位移不再为零,因此除了力的传递率 μF外,还可以求得位移的传递率 μX,按照前面的方法,可求得力的传递率:

以及位移传递率:
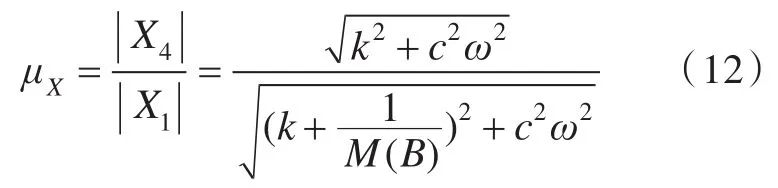
式(11)和式(12)中的 M(B)指基础在支架固定位置B点处的位移导纳。由此可知,力的传递率 μF不仅与 k,c,ω 有关,而且还与管道导纳M(A)以及导纳 M(B)有关;而位移传递率 μX则与管道在 A点的导纳 M(A)无关,只与 k,c,ω以及导纳M(B)有关。
假设管路支架的基础为一四边简支、边长为a、厚度为h的方形薄钢板,管路支架固定在板上的B点(实际上支架可能有多个脚,但脚之间的距离相对板长较小,这里把它看成一个点),由薄板振动理论可求得:
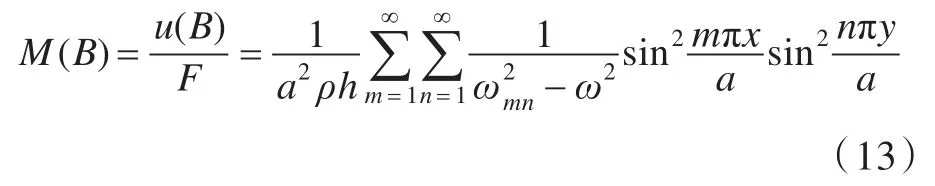
式中,,为简支板固有频率,其中,为抗弯刚度,ρ为钢板密度,E为弹性模量,σ为泊松比。当B点位于板的中点时,x=y=a/2,将式(13)代入位移传递率公式(13),得

2.2 传递率曲线
为研究隔振系统中各因素对传递率的影响,假设基础板边长a=2m和厚度h=0.02m,密度ρ=7.8×103kg/m3,其余参数与前面一致。代入式(13)和式(14),分析各因素对力的传递率与位移传递率曲线的影响如下:
1)弹性基础对力传递率 μF的影响。与前面基础固定时的传递率曲线进行对比,管用弹性支承梁模型代替,管路支架的垂向刚度k1=5×105N/m。两种情况下力传递率μF随激励力频率ω的变化曲线如图12所示。由该图可知,考虑基础弹性时,力的传递曲线在 ω=151.75 rad/s和 ω=758.78 rad/s时出现了2个峰谷值,而这2个频率正好对应简支板的ω11和ω13这两阶固有频率,这说明2个峰谷值是由基础的第(1,1)和(1,3)阶固有振型被激发所引起,并且越靠近主峰由基础被激发引起的峰值越大,反之亦然。实际上,随着激励力频率ω的扩大,基础的所有奇数阶振型都会被激发,而在未被激发的偶数阶固有频率处则不会出现峰谷值。从总体来看,基础弹性对力传递率的影响较小。

图12 基础弹性对力传递率的影响Fig.12 Influence of the elasticity of infrastructure on transfer rate of force
2)管路支架刚度对位移传递率的影响。按照前面,选两组不同刚度的支架进行比较,得到位移传递率曲线的对比图,如图13所示。

图13 支架刚度k对位移传递率曲线的影响(h=0.02m)Fig.13 Influence of the stiffness ofpiping support(k)on transfer rate of displacement(h=0.02m)
图13 中两条曲线各个峰值所对应的频率相近,即都在基础板的奇数阶固有频率附近,且刚度小的μX曲线峰值明显更小。并且在绝大部分频率范围内,刚度小的 μX曲线都在刚度大的 μX曲线下方,说明刚度是影响支架位移隔振的重要因素,刚度小的支架对位移隔振效果更好。
3)支架固定位置对位移传递率的影响。前面分析的都是以支架固定在板中点(a/2,a/2)为前提,改变支架固定位置,增加(a/4,a/4)和(a/8,a/8)两个位置进行对比分析,得到3种情况下的位移传递率曲线如图14所示。由该图可看出,3种情况下,固定位置越靠近边缘,μX曲线峰值越小,且位置越低。一般情况下,当支架固定在基础边缘靠近板支撑的位置时,将得到更好的位移隔振效果。另外,基础板的厚度和大小也会对μX曲线峰值的数量和位置产生一定的影响,一般来说,基础板越厚、越小,M(B)就越小,位移隔振效果也越好。
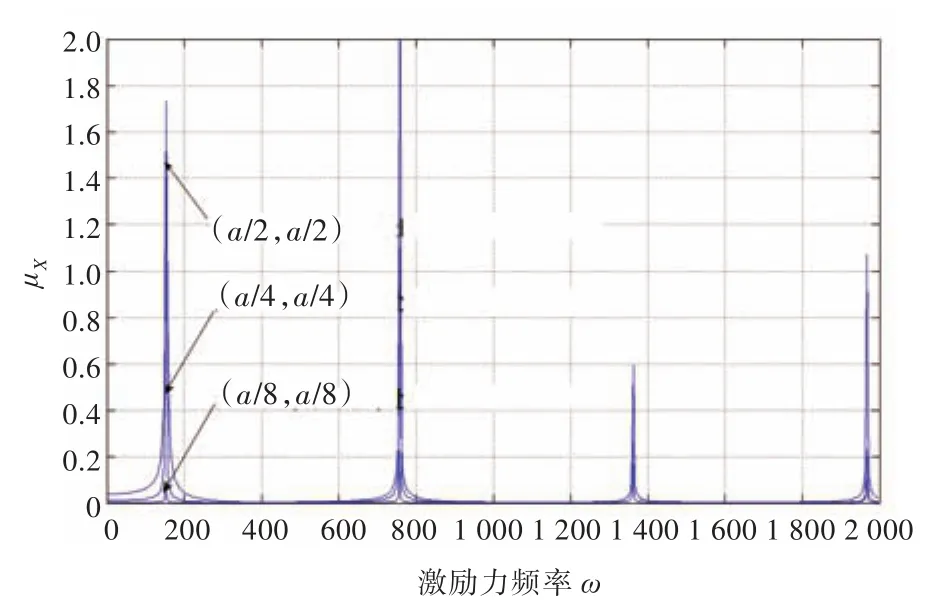
图14 基础板上不同安装位置对位移传递率的影响Fig.14 Influence of fixed position of piping support on transfer rate ofdisplacement
4)支架阻尼对位移传递率的影响。参照前面的方式设置两组阻尼对比,如图15所示。该图说明,阻尼除了对曲线峰值起到了一定的抑制作用外,对位移传递率的影响也很小。
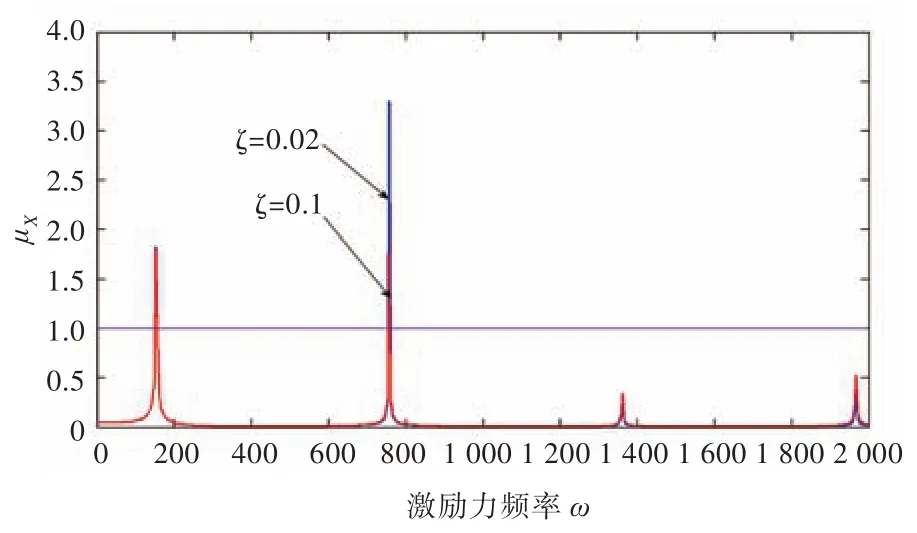
图15 支架阻尼对位移传递率曲线的影响Fig.15 Influence of the damping of piping support on transfer rate of displacement
3 有限元仿真
在上面分析的基础上,利用有限元软件建立实体模型,通过含预应力的谐响应分析进行仿真验算。这里,以船舶中常用的硫化马脚作为计算对象,它一般包含硫化卡箍、橡胶垫、支座等多个构件,通过螺栓固定在一起。前面已经证实,位移传递率与管道特性无关,为简化计算,管长只取0.1 m。另外,用壳单元模拟基础板,壳单元与支架体单元之间通过多点约束(MPC)技术连接在一起。其他参数与前面一致,考虑阻尼,利用软件自带的计算功能,得到的基础与管垂向位移比 μX(即位移传递率)曲线如图16所示。
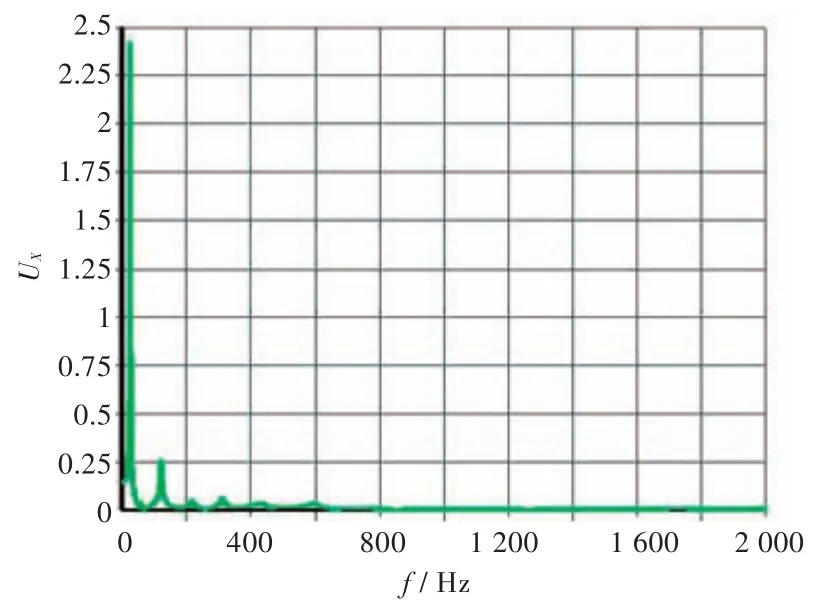
图16 有限元计算的支架的垂向位移传递率Fig.16 Transfer function ofdisplacementof piping support in the verticaldirection by finite element calculation
将图16中的曲线与图13理论计算得到的刚度k1=5×105N/m的位移传递率 μX曲线进行比较,并将横轴圆频率换算成角频率,发现两曲线峰值位置一致,只是幅值不同,应为设置的阻尼引起。可见,前面的理论计算与有限元求解的结论基本一致。
4 结论及建议
通过理论求解和有限元计算的验证分析,可以得出以下结论:
1)影响管路支架隔振性能的首要因素是支架的刚度,另外支架实际所处的安装环境,包括管道和基础的弹性,也会对支架隔振性能产生较大影响。因此,在研究管路支架隔振性能时,应综合考虑各个因素的影响。
2)通过对评价管路支架隔振性能常用的2个指标(力隔振和位移隔振)进行分析,可以得知:力隔振能更准确地反映支架的隔振性能,但由于实测较困难,在工程中应用较少;位移隔振受基础特性的影响较大,所得结论容易产生偏差,但由于实测方便,在工程中应用比较广泛。
通过本文的分析,可以得到一些改善管路支架隔振性能的建议:
1)对于高频激励,尽量降低支架刚度,这是提高支架隔振性能的关键。在实际工作中,可通过增加橡胶圈层数,增大橡胶垫厚度,采用硫化马脚,加装隔振器,调整支架形状和紧固程度等来实现。
2)对于低频激励,低刚度支架往往不利于隔振,应首先根据计算选择合适的刚度,以避开峰值获得最佳隔振效果。
3)当支架刚度已给定时,可以通过计算调整支架间距来获得较好的隔振效果。
4)支架应尽量安装在较坚固的结构上。当安装在船体板上时,应尽量靠近肋骨或加强筋,这样有助于提高管路与船体间位移的隔振效果。
5)引入适当的阻尼。基于阻尼的减振耗能作用,其能改善振动的平稳度并抑制峰值,对于隔离结构的振动具有一定的作用。
[1]戴安东,陈刚,朱石坚.舰船管路振动噪声控制措施综述[J].船海工程,2001(增刊2):75-78.
DAI A D,CHEN G,ZHU S J.Overview of the ship pipe working vibration and noise control[J].Ship and Ocean Engineering,2001(s2):75-78.
[2]JANSSON L G,ZENG L F.On modeling piping supports in dynamic analysis of nuclear-power piping system[C]//Proceedings of the 16th International Conference on Nuclear Engineering,2008:277-283.
[3]李维嘉,曹青松.船舶振动主动控制的研究进展与评述[J].中国造船,2007,48(2):68-79.
LIW J,CAO Q S.Advances and review on the research of the active control of ship vibration[J].Ship Building of China,2007,48(2):68-79.
[4]RIVIN E I.Passive vibration isolation[M].New York:ASMEPress,2003.
[5]王育平,张丹才,余永丰.通海系统管路阻尼处理降噪技术研究[J].噪声与振动控制,2010,30(4):40-43.
WANG Y P,ZHANG D C,YU Y F.Research on damping material used in sea pipeline systems[J].Noise and Vibration Control,2010,30(4):40-43.
[6]蒋学武,朱石坚.舰船管路橡胶减振器的应用[J].海军工程大学学报,2000,93(4):90-91,94.
JIANG X W,ZHU S J.The application of pipe rubber vibration isolators on warships[J].Journal of Naval University of Enginering,2000,93(4):90-91,94.
[7]朱石坚,楼京俊,何其伟,等.隔振理论与隔振技术[M].北京:国防工业出版社,2006.
[8]SCIULLID,INMAN D J.Isolation design for a flexible system[J].Journal of Sound and Vibration,1998,216(2):251-267.
[9]高爱军.基于四端参数分析法的鱼雷动力隔振技术研究[J].鱼雷技术,2007,15(1):29-32.
GAO A J.Research on vibration isolation for torpedo power based on four-end parameter analysis method[J].Torpedo Technology,2007,15(1):29-32.
[10]YANG Y B,LIN C L,YAU JD,et al.Mechanism of resonance and cancellation for train-induced vibrations on bridges with elastic bearings[J].Journal of Sound and Vibration,2004,269(1/2):345-360.
[11]宋殿义,蒋志刚,陈北雁.弹性支承梁自振频率分析[J].江苏建筑,2005,99(1):30,38.
SONG D Y,JIANG Z G,CHEN B Y.Analysis on self-vibrationfrequency of strut beam[J].Jiangsu Construction,2005,99(1):30,38.
[12]尹泽勇,陈亚农.卡箍刚度的有限元计算与实验测定[J]. 航空动力学报,1999,14(2):179-182.
YIN Z Y,CHEN Y N.Finite element analysis and experimentalmeasurement of stiffness of hoop[J].Journalof Aerospace Power,1999,14(2):179-182.

