提高船用阻尼材料应用效果的优化设计方法
蒋亚礼 吕林华 杨德庆
上海交通大学海洋工程国家重点实验室,上海200030
0 引 言
阻尼材料是利用高分子材料的粘弹性将振动机械能转化为热能消耗掉,从而达到减振降噪目的的一种材料。各种形式的阻尼材料目前已广泛应用于航空航天、汽车、船舶及建筑等诸多领域[1]。在水面舰船和潜艇中主要振源所在的船体、基座、舱壁、甲板以及对居住性要求较高的舱室内,均大量采用阻尼材料抑制振动[2]。在浮筏或舱筏隔振装置上,也大量采用阻尼材料来抑制共振,降低筏架结构的局部振动响应,提高浮筏装置的隔振效果。
衡量材料阻尼特性的参数是材料损耗因子。大多数阻尼材料的损耗因子会随环境条件的变化而变化,其中温度和频率对损耗因子具有重要影响。现行的声学阻尼材料测试国家标准[3-4]规定了采用阻尼样条或复合试样样条的阻尼损耗因子悬臂梁或自由梁测量方法。
在常用的阻尼材料中,高阻尼合金具有耐高温、工艺简便、适用范围广等优点,但其阻尼性能低,与粘弹性阻尼材料比相差1~2个数量级,不能用于许多高阻尼要求的场合[5]。粘弹性阻尼材料的阻尼损耗因子虽然较高,但材料易于老化,使用期短,其阻尼特性受温度的影响也较大,同时其刚度、强度和抗蠕变性也较差,不能作为结构材料使用,只有在与其他结构材料复合形成一定的阻尼结构后才能发挥作用[6]。因此,为了满足环境与工艺的要求和提高阻尼材料的减振降噪效率,近年来,国内外许多研究人员对复合阻尼材料进行了大量研究。在工程结构的振动控制中,为了改善结构的动力学性能,降低结构动响应水平,通常借助优化设计手段来对复合材料进行优化设计[7]。在传统的阻尼材料减振设计中,阻尼材料完全覆盖于待控结构表面,结构参数设计只是确定使结构损耗因子取最大值时的阻尼材料类型、层数和厚度等。传统的减振设计很难通过阻尼材料的分布,以最小的阻尼材料用量达到指定的减振要求[8]。杨德庆[9]针对自由阻尼结构的耗能特点,提出了阻尼胞单元和阻尼拓扑敏度等概念,对自由阻尼层结构进行了阻尼材料优化配置。汪浩等[10]对复合板阻尼材料的减振性能进行了试验研究。本文将基于模态应变能法及结构动力学优化理论,研究提高船用阻尼材料应用效果的多种方法,包括在阻尼材料上开一定百分比的孔、优化阻尼材料在控制对象表面的分布[11],使其在满足指定的减振要求下用量最少。
1 等效模态阻尼损耗因子计算方法
将模态分析的理论或有限元方法应用于阻尼复合结构,使用模态参数与能量法,可求得阻尼复合结构各阶等效模态损耗因子的表达式。对于阻尼复合结构,其位移与应变的关系式为:

式中,为几何矩阵;为节点位移列阵。
应力与应变间的关系为:

式中,为弹性矩阵。将式(1)代入式(2),可得到应力与位移的关系为:

每一单元的应变能为:

将式(1)代入式(4),得
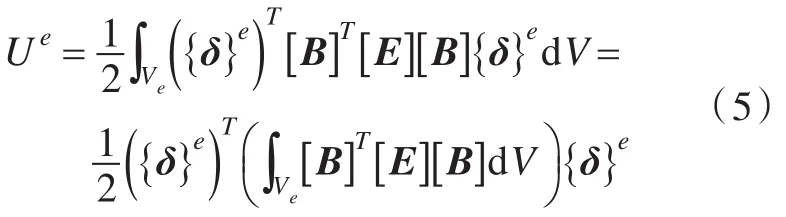
令为单元刚度矩阵,它由两部分组成,即

式中,为基层的单元刚度矩阵;为阻尼层的单元刚度矩阵。因此,单元应变能可表达为:

经整体组装,得到总应变能和总动能分别为:
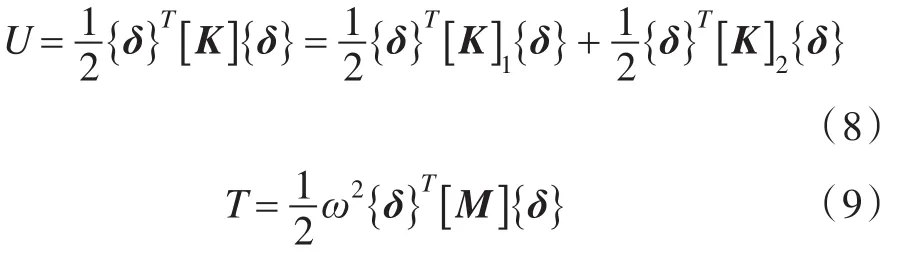
基层和阻尼材料耗散的能量分别为:
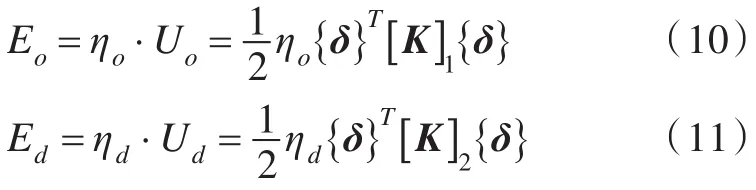
因此,复合结构第k阶等效模态损耗因子为:

式(8)~式(12)中,为总刚度矩阵,和分别为基层和阻尼层的总刚度矩阵,为总体节点位移列阵,为总质量矩阵,ηo和ηd分别为基层和阻尼层材料的损耗因子,Uo和Ud分别为基层和阻尼层材料的应变能。若不考虑能量损耗,根据变分原理可得:

将式(8)和式(9)代入式(12),得到方程:
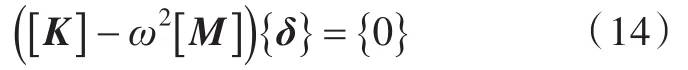
解方程(13),得特征值ω和振型,然后将求得的代入式(8)、式(10)和式(11),即可求得复合结构的等效模态损耗因子。
2 提高阻尼材料减振效果的方法
2.1 阻尼材料一定百分比开孔法
选取两端边界均为简支的钢管,外径89mm,壁厚3mm。钢的材料参数为:密度ρ=7 860kg/m3,弹性模量E=200GPa,泊松比γ=0.3,材料阻尼损耗因子为0.8%。钢管外包覆一层8mm厚的阻尼材料。阻尼材料选取DFM,材料参数见表1,其中密度 ρ=1 420 kg/m3,阻尼材料的泊松比 γ=0.49。表中,频率为材料的固有频率,储能模量为材料的弹性模量,tanδ为材料的阻尼损耗因子,为损耗模量与储能模量的比值。
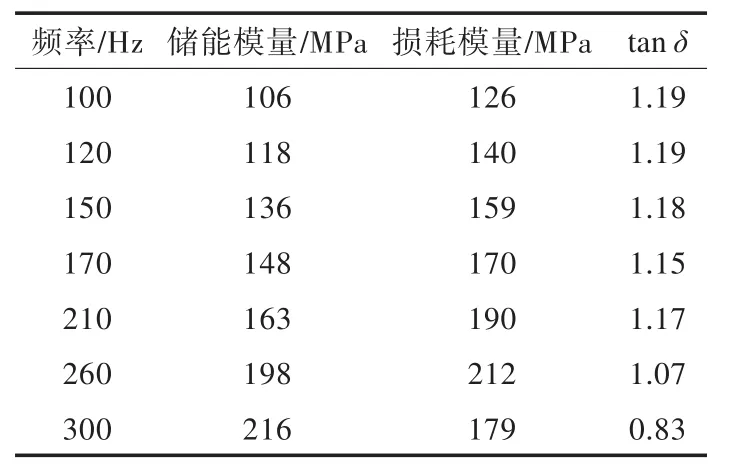
表1 DFM材料参数(25℃)Tab.1 The param etersof DFM(25℃)
阻尼材料为矩形穿孔结构,孔结构尺寸为:长6mm、宽3mm、深6 mm,穿孔率为16.6%,如图1所示。有限元模型如图2所示。
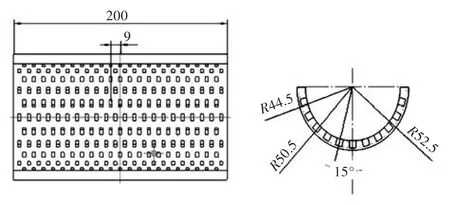
图1 管模型二维结构图Fig.1 Two-dimensional drawing of the pipe

图2 阻尼材料矩形穿孔的有限元模型Fig.2 FEM model for the damping layerwith rectangle holes
采用上述模态应变能法计算出的开孔阻尼结构损耗因子如表2所示。在确保同等阻尼材料使用量的前提下,对比了穿孔结构和实心结构的模态损耗因子。穿孔结构阻尼的穿孔率为16.6%,可减小实心结构上阻尼材料的厚度以保持阻尼材料使用量一致。
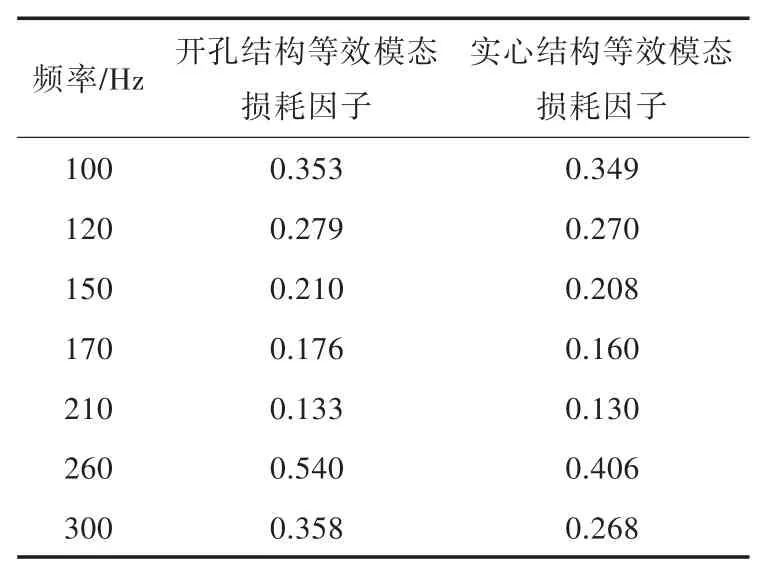
表2 不同频率下开孔结构和实心结构等效模态损耗因子计算结果Tab.2 The calcu lation resu lts of equivalen tm odal loss factors for opening structure and solid structu re in various frequences
通过对比表2中开孔阻尼结构与实心阻尼结构的数据不难发现,在阻尼材料使用量相同的情况下,相比于实心结构,开孔结构的等效模态损耗因子更高。
2.2 重量目标函数及考虑损耗因子约束的阻尼材料优化
参照GB/T 18258-2000,选用自由长度为200 mm、宽10 mm、厚2 mm的钢条基片上涂有2 mm厚阻尼材料的复合板,通过悬臂梁法进行数值计算分析。阻尼材料的参数如表3所示。

表3 SA-3阻尼材料的参数Tab.3 Param eters of SA-3
采用Patran/Nastran有限元分析软件对实际结构进行建模分析,其中,钢基板采用块体单元,阻尼材料采用壳体单元,在板的左端进行固定约束,使其成为悬臂板,具体如图3所示。表4给出了结构的10阶固有频率以及损耗因子。

图3 阻尼材料分区域厚度优化设计变量分布示意图Fig.3 Sketch of design variables for the thickness optimization distribution of dampingmaterial

表4 复合阻尼板的频率及损耗因子Tab.4 Natural frequenciesand dam p ing loss factors of com posite dam ping p late
2.2.1 重量目标函数及考虑损耗因子约束的阻尼材料厚度优化
将阻尼材料的分布分为8个区域(图3),各个区域阻尼材料的厚度不同,同一区域阻尼材料的厚度相同。以各个区域阻尼材料厚度为设计变量进行优化设计,使得到的指定阶次模态阻尼系数(或阻尼损耗因子)处于一定的约束范围之内,从而实现预期的减振要求。
在本优化模型中,以各个区域阻尼材料的厚度为设计变量ti(i为区域编号),厚度设计变量的尺寸上下限约束分别为和。以阻尼材料重量为目标函数,整体结构的等效模态损耗因子在指定范围内作为约束。数学表达式为:
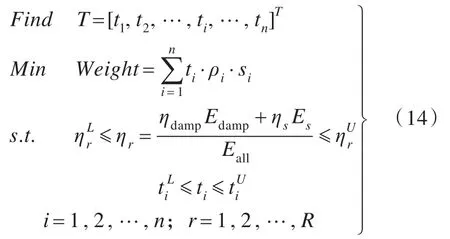
式中,ρi和si分别为单元材料密度和面积;和分别为待设计结构损耗因子的上限和下限。其中,0.1mm≤ti≤8mm ,0.04≤ηr≤0.042。
对于简化的优化模型,采用ISIGHT软件中的多岛遗传算法进行求解,得到最终的优化结果如表5和表6所示。
由表5可看出,优化后的阻尼材料厚度值均在约束范围内,满足设计变量的约束要求。观察表6可知,经优化后,复合阻尼材料悬臂板的前3阶模态损耗因子均满足减振要求,使用的阻尼材料重量达到最小,且复合板固有频率越低时,其结构损耗因子越大,减振效果越好。
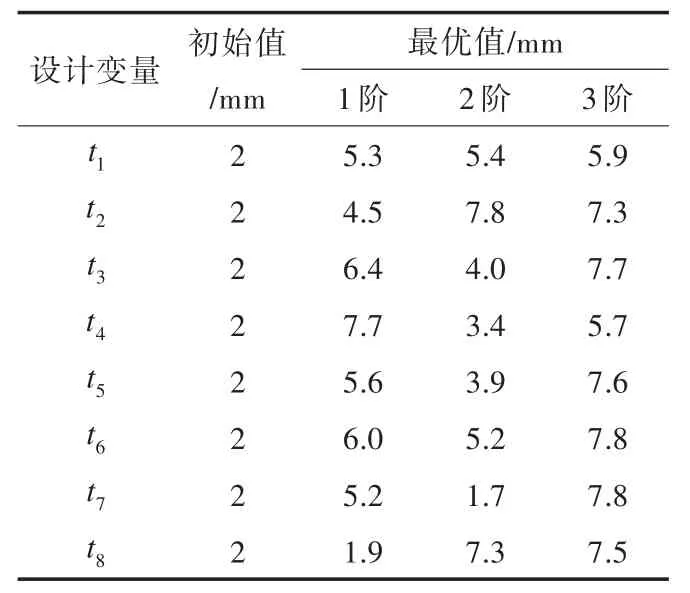
表5 优化后阻尼材料各区域厚度值Tab.5 Op tim ized p late thickness in d ifferent areas

表6 优化后阻尼材料层的重量与结构的等效模态损耗因子Tab.6 Optim ization resu lts for theweight of dam ping m aterialand m odal loss factors of structure
悬臂梁的1阶模态为弯曲模态,从实际经验来看,固定端区域7和区域8的阻尼材料厚度对结构的等效模态损耗因子影响也最大。但从表5中能看出区域3和区域4的阻尼材料厚度值最大,所以对复合结构阻尼损耗因子的影响也最大。为了验证这一结果,对比了2种阻尼材料贴敷情况下评价点的加速度响应:
情况1:在区域3和区域4处贴敷7.7mm厚的阻尼材料,其他区域不贴;
情况2,在区域7和区域8处贴敷7.7mm厚的阻尼材料,其他区域不贴。
在节点A1处施加10~200 Hz的单位激振力,取B1和B2作为响应评价点,如图4所示,其计算结果如图5所示。由图5可知,在情况1下,两个响应评价点(B1和B2)的平均振级要小于情况2下这两点的平均振级。这说明,区域3和区域4的阻尼材料对复合结构阻尼损耗因子影响较大,验证了本文提出的阻尼材料配置优化结果减振最为有效。

图4 激振点和评价点示意图Fig.4 The placementofexcitation and evaluation points on the plate
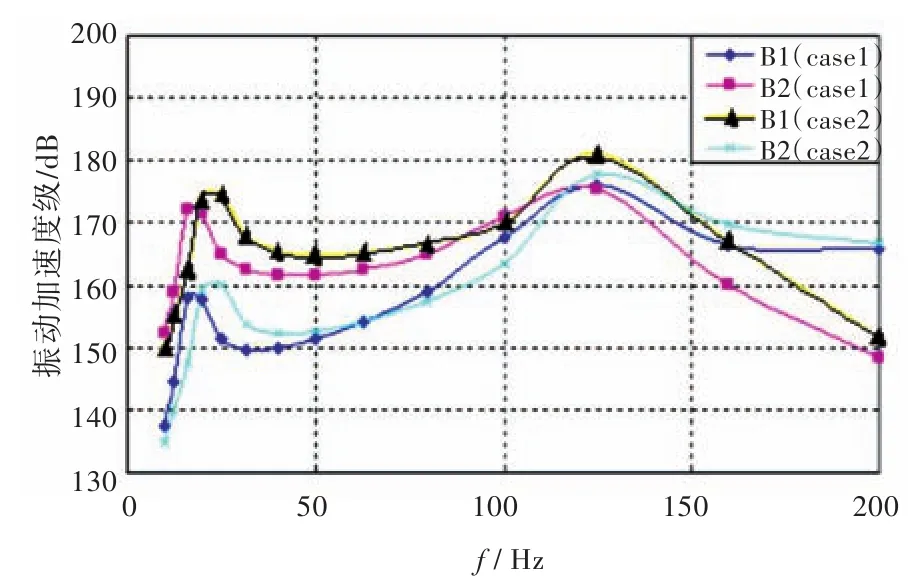
图5 评价点的加速度振级Fig.5 Vibration levelof the referenced points
2.2.2 重量目标函数及考虑损耗因子约束的阻尼材料拓扑分布优化
设计变量 T=[t1,t2,…,ti,…,tn]T为 n 维阻尼材料拓扑分布设计变量向量,其分量只能取0或1。其中,0表示该区域没有阻尼材料,1表示该区域有6mm厚的阻尼材料。优化数学表达式为:
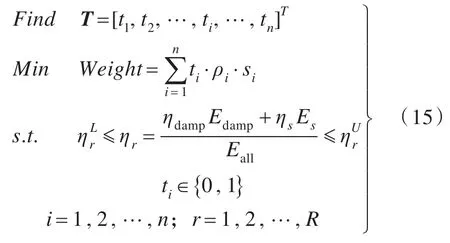
其他变量的含义与式(14)同。
对于简化的优化模型,采用ISIGHT软件中的多岛遗传算法进行求解,得到的最终优化结果如表7和表8所示。
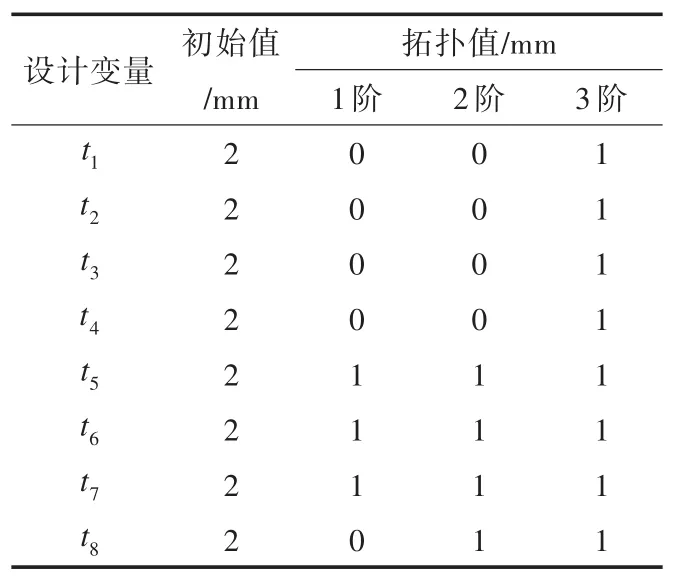
表7 优化后阻尼材料各个区域拓扑值Tab.7 Op tim ization resu lts for the topology valuesof dam pingm aterial in different areas
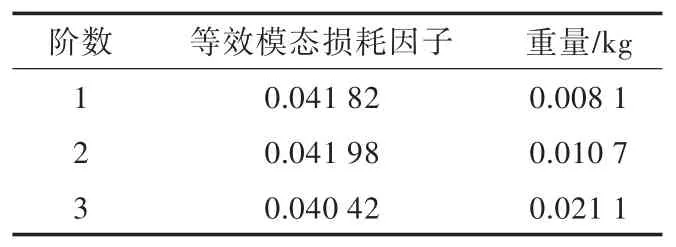
表8 优化后阻尼材料层的重量与结构的损耗因子Tab.8 Op tim ization resu lts for theweigh t of dam p ing m aterialand m odal loss factors of structure
由表7可看出,优化后的阻尼材料厚度值均在约束范围内,满足设计变量的约束要求。观察表8可知,经优化后,复合悬臂板前3阶模态在满足结构减振要求下,所使用的阻尼材料重量均达到最小,且复合板固有频率越低时,其结构所用阻尼材料也越少。
优化后的复合板阻尼材料分布如图6~图8所示。

图6 1阶优化后阻尼材料厚度分布图Fig.6 Optimization results of the thickness of dampingmaterials in the 1stmode

图7 2阶优化后阻尼材料厚度分布图Fig.7 Optimization results of the thickness of dampingmaterials in the 2ndmode

图8 3阶优化后阻尼材料厚度分布图Fig.8 Optimization results of the thickness of dampingmaterials in the 3rdmode
3 结 论
本文对比研究了开孔阻尼材料与实心结构间减振效果,以及阻尼材料的优化配置问题。建立了以阻尼材料重量为目标函数、结构损耗因子为约束条件的优化模型,包括阻尼材料厚度优化以及给定厚度下的阻尼材料拓扑分布优化。研究结果表明:
1)在阻尼材料使用量相等的前提下,相比于实心结构,开孔结构的损耗因子更大,其结构更有利于能量的耗散,效果更好。
2)采用重量目标函数及考虑损耗因子约束的阻尼材料厚度值优化和拓扑分布优化方法,经优化,复合板厚度设计变量均满足约束条件,复合板前3阶模态损耗因子均满足结构减振要求,而使用的阻尼材料重量也达到最小。
3)采用拓扑分布优化方法所得的复合板结构损耗因子均高于采用厚度值优化方法所得的复合板结构损耗因子。相比阻尼材料厚度值优化方法,拓扑分布优化方法在提高船用阻尼材料的应用效果方面效果更佳。
[1]SONG Z L,MA LQ,WU Z J,etal.Effects of viscosity on cellular structure of foamed alum inum in foaming process[J].JournalofMaterials Science,2000,35(1):15-20.
[2]XIE Y M,STEVEN G P.Evolutionary structural optimization[M].Berlin,Heirlelberg,New York:Springer,1997.
[3]中国科学院声学研究所,等.GB/T16406-1996 声学材料阻尼性能的弯曲共振测试方法[S].全国声学标准化委员会,1996.
[4]ASTM E756-04 standard testmethod for measuring vibration-damping properties ofmaterials[S].美国材料与测试学会,2004.
[5]张忠明,刘宏昭,王锦程,等.材料阻尼及阻尼材料的研究进展[J].功能材料,2001,32(3):227-230.
ZHANG ZM,LIU H Z,WANG JC,et al.Damping of material and progress in the damping materials[J].Journal of Functional Materials,2001,32(3):227-230.
[6]孙庆鸿,张启军,姚慧珠.振动与噪声的阻尼控制[M].北京:机械工业出版社,1992:1-60.
[7]戴德沛.阻尼技术的工程应用[M].北京:清华大学出版社,1991.
[8]李以农,谢熔炉,王宜,等.约束阻尼结构拓扑优化设计的进化算法[J].重庆大学学报,2010,33(8):1-6.
LIY N,XIE R L,WANG Y,et al.Topology optimization for constrained layer damping material in structures using ESOmethod[J].Journal of Chongqing University,2010,33(8):1-6.
[9]杨德庆.动响应约束下阻尼材料配置优化的拓扑敏度法[J].上海交通大学学报,2003,37(8):1109-1212,1225.
YANG D Q.Topological sensitivitymethod for the optimal placement of unconstrained dampingmaterials under dynamic response constraints[J].Journal of Shanghai Jiao Tong University,2003,37(8):1109-1212,1225.
[10]汪浩,肖邵予.阻尼材料减振性能试验研究[J].中国舰船研究,2009,4(1):38-42.
WANG H,XIAO S Y.Experimental study on damping properties of acoustical materials[J].Chinese Journalof Ship Research,2009,4(1):38-42.
[11]郑玲,谢熔炉,王宜,等.基于优化准则的约束阻尼材料优化配置[J].振动与冲击,2010,29(11):156-159,179.
ZHENG L,XIE R L,WANG Y,et al.Optimal placement of constrained damping material in structures based on optimality criteria[J].Journal of Vibration and Shock,2010,29(11):156-159,179.

