一种高容积阻力比水下热滑翔机壳体外形设计
周徐斌 马 捷
海洋工程国家重点实验室上海交通大学,上海200240
0 引言
水下热滑翔机是一种高效环保、浮力驱动、低噪声的自主式水下运载器,可广泛应用于海洋科学考察以及军事领域。但是,由于海洋温跃层的温差较小(往往不超过20℃),温差能的能量品质较低,导致水下热滑翔机的热机效率不仅较低,而且功率往往也不大,因此,需要寻找具有最低阻力特性的壳体外形,以使滑翔机摆脱温差功率的限制,实现低功率运行,高续航周期的服务。同时,热滑翔机作为一种水下运载器,不仅需要装载自身航行所需的动力装置、控制系统和大量传感器,而且还要装载为实现特殊功能和满足工作需要的大量科研仪器设备,因此,所设计的滑翔机壳体外形必须具有较强的装载能力,否则,将严重限制滑翔机的实际工作性能。
文献[1-2]采用数值计算的方法对水下航行器,如潜艇、水下滑翔机等的低阻特性进行了研究,并且计算了在不同速度下壳体外形的阻力随攻角的变化曲线以及其压力云图等水动力数据。本文旨在此基础之上,通过分析不同壳体外形周围绕流场的情况并总结其优缺点,综合考虑水动力和装载能力两方面的性能,提出一种能够克服滑翔机壳体外形的低阻特性与装载能力之间矛盾的新型高性能壳体外形。
本文在水下热滑翔机壳体外形的设计中,首先将提出一个无量纲的容积阻力比系数,该系数是衡量滑翔机壳体外形的低阻性能和装载性能的综合指标,该系数越大,说明壳体外形这两方面的综合性能越好,反之则越差。其次,本文将以4种常见壳体外形为基本出发点,通过数值计算的方法,分析出它们各自的优缺点。之后,再采用扬长避短、各取所长的设计思想,结合纺锤体外形的低阻力特性和椭球体头尾外形的高装载特性的优点,设计出一种具有高容积阻力比的水下热滑翔机壳体外形,该外形在具有较好的低阻特性的同时又具有较强的装载能力。
1 水动力数值计算的理论基础
本文不考虑流体的热效应,只关注流场的速度分布和阻力大小。本章将基于质量守恒、动量守恒定律,推导计算水动力学的控制方程。
1)质量连续方程
质量连续方程保证了流体流动的连续性,即单位时间内流体任何体积单元中质量的增加,等于同一时间间隔内流入该体积单元的净质量,由于滑翔机周围流体的速度较慢,不考虑流体密度的变化,所以

式中,i=1,2,3,分别代表水动力数值计算的三维正交坐标系中的3个维度;u为速度;x为流场空间点坐标。
2)动量连续方程
动量连续方程保证了经典力学中的动量定律,即数值计算的体积单元中流体的动量对时间的变化率等于外界作用在该体积单元上的各种外力之和。由于滑翔机周围的流体为海水,因此,忽略流体膨胀粘性系数,并将流体粘性系数视为常数,则动量连续方程为:
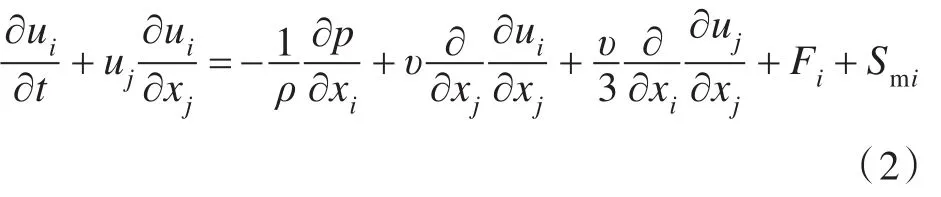
式中,i,j=1,2,3,分别代表三维正交坐标系中的3个维度;υ为流体的运动粘度系数;p为压力,Pa;ρ为密度,kg/m3;F为体积单元所受的外力,N;Sm为流体质量源(汇)。
3)湍流k-ε方程
本文采用雷诺平均(RANS)算法对滑翔机壳体周围的湍流流动进行计算,即将湍流的N-S方程组对时间进行平均,滤掉高阶小量,得到雷诺时均方程组。本文所讨论的壳体周围流体的运动雷诺数在105数量级,引入适用于非较高雷诺数情况下的湍流动能和湍流耗散率的标准k-ε方程使各方程封闭,如式(3)和式(4)所示:

式中,k为湍流动能,m2/s2,;ε为湍流耗散率,,;Gs和GT均为附加湍流生成项,其中gi为重力加速度在i方向上的分量,T为湍流质点的温度,℃;μt为湍流粘性系数,,其中Ct为一个常数。相关的其他常数值按1972年Launder-Spalding的建议,取值如表 1所示[3]。

表1 k-ε方程相关参数Tab.1 Param etersof k-εfunction
4)壁面函数
如果将壁面作为光滑壁面处理,则流体不会因为摩擦受到来自壁面的阻力作用,这与实际情况不符,同时也会给流场的计算带来误差,尤其是在雷诺数不高而又使用k-ε模型的情况下,甚至还会造成较大误差。为此,本文根据文献[4]和文献[5]的研究,引入壁面函数,即在壁面附近流体的速度分布公式,如式(5)所示:

式中,k为卡尔曼数,k=0.4;A为常数,A=5.5;y为流体质点距壁面的距离,m;u*为流体质点相对壁面的摩擦速度,m/s,,其中 τ0为壁面剪应力,N。

式中,当>1 000时,该范围内壁面流体的作用力 τ=ρu*2,N。
2 对4种常见壳体外形的综合性能分析
2.1 4种常见壳体外形的几何模型
本文研究的水下热滑翔机壳体外形的总体主尺寸总长1.5m,最大直径0.2m。一方面,由于这2个参数与水动力性能计算的壳体外形的周围绕流流场的特征有关[6],另一方面,为便于分析比较,本文在水下热滑翔机壳体外形的研究中将这2个参数的值保持不变,4种常见壳体外形的几何模型如图1所示,从球体首尾外形壳体到纺锤体壳体,外形逐渐变得细长尖削。
2.2 4种常见壳体外形的低阻特性分析
2.2.1 计算边界与网格
数值计算的流体域是一个长4.5m、宽0.5m、高0.5m的长方体域,流场的来流边界距滑翔机壳体的头部1.4m,去流边界距尾部1.6m。相对滑翔机机身的尺寸(长1.5m,横截面的最大直径0.2 m)而言,流体域的尺寸足够大,确保了在计算滑翔机水动力性能时流场的进流和尾流都能充分发展,从而保证了数值计算的可靠性[7]。来流边界设置为固定流速0.5m/s的边界条件,去流边界为可自由流出的全压为零的边界条件,如图2所示(以椭球体首尾外形为例)。

图1 4种常见的壳体外形设计方案Fig.1 Gallery of four common shellshape designs

图2 数值计算流场域示意图Fig.2 The flowing area for numerical calculation
结构化网格具有生成速度快、网格质量好、收敛性较高等优点,因此,本文对流体域采用正交六面体结构化网格来进行划分,如图3所示。以椭球体首尾外形壳体的计算模型为例,共计3 531 000个网格。图3(a)为网格划分完毕的椭球体首尾外形壳体的流场域正视图,图3(b)为侧视图。

图3 数值计算流场域网格划分示意图Fig.3 Mesh of the flowing area applied in the numerical calculation
流体域的进流远端和去流远端采用粗网格,如图3所示的浅色线边长(10~16mm)部分。由于这部分流场与壳体的相互作用以及流动变化已经较小,因而粗网格既可以保证足够的精度,又可以减少网格总数,达到减轻计算负荷的效果。在壁面附近及流动发生剥离和涡旋形成的地方,则采用精细网格,如图3所示的深色网格线边长(3.5~7mm)部分。一方面,要保证滑翔机壳体外形的复杂型线能够被准确刻画,另一方面,也能保证计算精度,以准确模拟这些区域的流体流动状态[8]。
同时,为保证网格质量,将不同边长的网格与网格之间的大小幅度变化率控制在1~1.1之间,粗细网格之间采用等比渐变的模式调整网格幅度,整个流体域内的网格长宽比(AspectRatio)也控制在1~6以内,最大长宽比为5.3∶1,没有极端畸变的网格。
采用有限体积法离散控制方程。由于采用高阶的六面体网格,对动量方程、湍流方程等采用二阶迎风格式离散,压力和速度的耦合迭代则采用SIMPLEC 算法[9]。
2.2.2 4种滑翔机壳体外形的阻力特性
在相同的收敛条件下(设质量平衡方程和动量守恒方程的最小相对收敛误差为10-7),采用STREAM软件和FLUENT软件求解器对第2.2.1小节中划分好网格和设置好边界条件的流场模型进行求解,得到水动力学数据,如表2所示。通过比对用2种软件分别计算第2.2.1小节所建立的流场域网格模型的数据结果,来验证两者的结果是否具有较高的一致性。
对采用2种求解器分别进行数值计算所得到的各外形的阻力数据进行比较可以发现:在压差阻力计算中,对椭球体首尾外形的求解偏差最大,为3.16%,对圆锥体首尾外形的求解偏差最小,为0.54%;在摩擦阻力计算中,对纺锤体外形的求解偏差最大,为4.23%,对圆锥体首尾外形的求解偏差最小,为0.26%。总而言之,分别采用FLUENT和STREAM进行数值计算得到的阻力数据的偏差均小于5%,结果表现出了较高的一致性,说明数值计算的结果是可靠的。
此外,根据表2中的数据,可知壳体模型的压差阻力起主导作用,相对而言,摩擦阻力的影响则较小。因摩擦阻力与雷诺数有关,在雷诺数保持不变的基础上,本文将重点分析压差阻力。
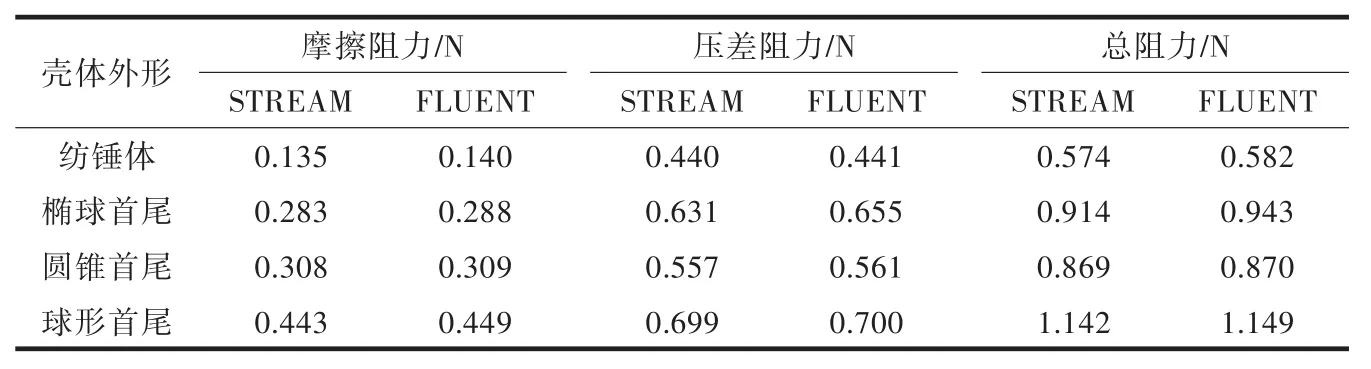
表2 STREAM和FLUENT求解各种壳体外形阻力系数计算结果比对表Tab.2 Com parison of drag coefficients calcu lation resu lts for d ifferen t shell shapesby STREAM and FLUENT
1)阻力系数
利用数值计算得到的结果,通过下式,可计算各滑翔机壳体外形的阻力系数C[10]:
drag
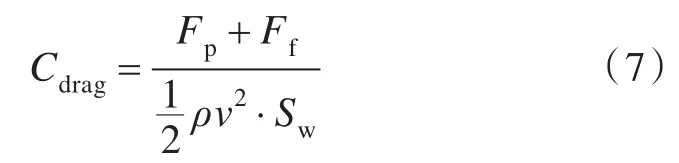
式中,Fp为压差阻力,N;Ff为摩擦阻力,N;为流体的动压,Pa;Sw为湿表面积,m2。
阻力系数是衡量滑翔机壳体外形阻力性能最重要、最直接的一个无量纲指标,因为它与水下航行物体在航行过程中所受的阻力成正比[11]。
根据数值模拟计算结果,利用式(7)计算各滑翔机壳体外形的阻力系数,整理后如表3所示。阻力系数由低到高排列分别为纺锤体外形、椭球体首尾外形、圆锥体首尾外形、球形首尾外形,可见外形越是尖削细长,阻力系数便越低。
2)速度矢量图分析

表3 4种常见壳体外形阻力系数表Tab.3 Drag coefficientof four comm on shell shapes
流场的速度矢量图表示稳态情况下流体域内各个节点的平均速度矢量,表征的是数值计算得到的流场各个体积单元流体质点的流速方向和大小。充分了解这些速度信息后就可以了解流场的整体情况,从而分析各种壳体外形的水动力性能发生差异的原因。根据阻力系数计算结果可知,低阻特性最好的是纺锤体外形,最差的是球形头尾外形。因此,利用速度矢量图对这两个极端情况进行分析,寻找滑翔机的阻力成因,可以为本文的设计提供思路。
本文主要观察流场域中壁面附近的流动,这部分流场与壳体之间的相互作用最为强烈,而在流场域中远离壁面的地方,由于远离边界层,且雷诺数不大,区域中显示为层流。
球形头尾外形的速度矢量图如图4所示。在球形头部,因来流受到阻滞,出现了锥形降速区(浅色区域)。由伯努利定理可知,这部分流体若失去速度,则该区域的压力会上升,从而产生压差阻力。

图4 球形首尾外形壳体周围流场速度矢量图Fig.4 Vector graph of the overall flow field around the shellwith ballhead and tail
由于尾部为球形,曲率变化急促,尾流还来不及过渡,使得原本紧贴壁面流动的边界层由于突然脱离壁面,一部分尾流会因动能耗尽且受到其它较快流体的挤压作用而成为倒流来填充相应的紧靠尾部的空间,因此,在尾部的三角形区域内可能会发生严重的边界层分离现象,这可以通过观察尾部速度矢量图来验证,如图5所示。由图可发现,在球形外壳的尾迹中出现了2个涡旋中心,这将导致较大诱导阻力的产生[12]。
纺锤体外形的速度矢量图如图6所示。由图可看出,流动无论是在头部还是在尾部始终都是平缓过渡。其中首部低速区的范围最为狭窄,降速幅度也不大,在尾迹中,既没有涡旋中心,也没有发生边界层分离现象,几乎没有较大的诱导阻力的产生,因此,其总体阻力最小。

图6 纺锤体外形壳体周围流场速度矢量图Fig.6 Vectorgraph of the flow field around the spindle shell
根据以上分析比较发现,尾部细长,且外形呈流线型,像纺锤体这样的二次曲率连续的型线的壳体在阻力特性方面具有较大优势,绕流平缓过渡;而型线较钝、尾部曲率变化较为急促的外壳则容易产生较大的压差阻力,从而使得低阻特性变差。
但如果计算这4种壳体外形的有效容积(可用于滑翔机装载的这部分容积结果整理如表4所示)又可发现:纺锤体外形的有效容积最低,这是因其形状过于细长;而球形首尾外形的低阻特性虽然最差,但却具有最大的有效容积,较尖削的圆锥体首尾外形和椭球体首尾外形的有效容积则居中。

表4 4种常见壳体外形有效容积Tab.4 Effective capacity of the four comm on shell shapes
综上所述,可总结出以下矛盾:呈流线型且尾部细长的壳体外形虽然具有较佳的低阻特性,但有效容积却较小。
2.3 容积阻力比系数
为解决第2.2小节中出现的低阻特性与有效容积之间的矛盾,更客观、合理地衡量滑翔机外壳的综合性能,根据实际设计过程中的需要,本文引入了一个无量纲的“容积阻力比”系数作为衡量水下热滑翔机壳体外形的可行性和综合性能指标。由于该系数的分子代表装载能力的高低,分母表征的是低阻性能,所以该系数的值越大,就说明该壳体既具有较大的装载量,同时又具有较低的阻力。

式中,Ve为所设计壳体的有效容积,m3;Vs为标准外壳容积[13],m3,其物理意义是在确定主尺度后外壳可能拥有的最大容积,可由下式计算:

式中,Ls为壳体的最大纵向长度,m;Bs为壳体的最大横向宽度,m;Hs为壳体的最大垂向高度,m。
3 新型滑翔机壳体外形
根据式(8)计算得到的各壳体外形的容积阻力比系数如表5所示。由表可见,椭球体首尾外形的容积阻力比系数最大,而纺锤体外形的容积阻力比系数则最小,这说明就综合性能而言,纺锤体外壳是最差的一种壳体设计方案。本文希望通过合理的设计,使外壳外形在阻力特性和装载能力这两方面都具有较好的表现。

表5 各壳体外形容积阻力比系数Tab.5 Capacity to d rag ratio of different shell shapes
在壳体外形设计中,本文充分发挥纺锤体外形和椭球体首尾外形各自的优势,采取将两者的优势结合起来的办法设计了一种新型的水下热滑翔机壳体外形(图7)。该壳体外形由3部分组成,其首部为一个长轴为0.2m,短轴为0.1m的半椭球体,尾部为纺锤体从拐点(即最大半径0.1m处)至尾端点的部分,中间段为将新的首部和尾部连接起来的圆柱体。这种壳体外形克服了纺锤体总体过于细长、有效容积小的缺点,但又最大程度地保留了纺锤体外形中起关键作用的低阻部分。
通过SOLIDWORKS软件计算,新型壳体外形的有效容积为0.038m3。

图7 新型水下热滑翔机壳体外形正视图Fig.7 Frontview ofnew designed shell shape of the ocean thermalglider
在阻力特性方面,对新型壳体外形利用STREAM软件进行了求解,并且使其边界条件和收敛条件与第2节的水动力计算的数值保持一致,计算得到的新型水下热滑翔机壳体外形的摩擦阻力、压差阻力、总阻力和湿表面积的数据如表6所示。以表6中的数据为基础,根据式(7)计算新型壳体外形的阻力系数,可得其结果为0.006。

表6 新型水下热滑翔机壳体外形水动力数据Tab.6 H yd rodynam ic data of the new designed shape shellof ocean therm alglider
最后,根据表6的水动力数据和式(8),计算出了新型水下热滑翔机壳体外形的容积阻力比系数,为1.200 1,其要比椭球体首尾外形高6.5%,比圆锥首尾外形高17.06%,比球体首尾外形高13.99%,比纺锤体外形高22.6%。
4 结 论
本文的出发点是利用CFD数值计算的方法来分析各种壳体外形的水动力性能,首先分别利用STREAM和FLUENT软件对具有相同边界条件和收敛条件的数值计算模型进行了求解,两者数值解的最大相对误差不超过5%,表现出了较高的一致性,说明数值解是可靠的。通过对数值计算得到的速度矢量图和阻力系数等进行分析比较,发现外形呈流线型且尾部尖而细长的壳体的低阻特性虽然较好,但有效容积小、装载能力较差。
在对水下热滑翔机壳体外形进行综合性能分析时,不仅要考虑壳体外形的低阻特性,还要考虑壳体外形的装载能力,因此,本文提出了一种采用容积阻力比系数来进行综合比较的方法。同时,还设计了一种半椭球首、纺锤体尾的新型壳体外形。与4种常见的滑翔机壳体外形相比,新型壳体外形具有最大的容积阻力比系数,是一种综合性能较高、低阻特性和装载能力较为平衡的外形设计方案,可作为水下热滑翔机壳体外形设计的一种新选择。
由于水下热滑翔机也属水下潜器的一种,在军事应用中就相当于一艘微型潜艇,因而本文有关水下热滑翔机壳体外形的水动力分析的研究对水下潜艇的设计而言也具有一定的借鉴意义。首先,本文采用正交六面体结构化网格对全流场域划分的方法也可以应用到潜艇壳体的水动力分析之中,它具有划分速度快、网格质量高、计算效率高等特点。其次,本文提出的容积阻力比系数既考虑了容积装载效率,又考虑了低阻特性,因潜艇同样也要考虑这两方面的综合性能,所以该系数也可以为某些潜艇的壳体外形设计提供参考。
[1]卢锦国,梁中刚,吴方良,等.水下航行体回转水动力数值计算研究[J].中国舰船研究,2011,6(6):8-12,27.
LU JG,LIANG ZG,WU F L,etal.Numerical calculation on hydrodynamic performance of the submerged vehicle in turning motion[J].Chinese Journal of Ship Research,2011,6(6):8-12,27.
[2]马冬梅,马铮,张华,等.水下滑翔机水动力性能分析及滑翔姿态优化研究[J].水动力学研究与进展,2007,22(6):703-708.
MA D M,MA Z,ZHANG H,et al.Hydrodynamic analysis and optimization on the gliding attitude of the underwater glider[J].Journal of Hydrodynamics,2007,22(6):703-708.
[3]柏铁朝,梁中刚,周轶美,等.潜艇操纵性水动力数值计算中湍流模式的比较与运用[J].中国舰船研究,2010,5(2):22-28.
BAO T C,LIANG ZG,ZHOU Y M,et al.Comparison and application of turbulencemodes in submarinemaneuvering hydrodynamic forces computation[J].Chinese Journalof Ship Research,2010,5(2):22-28.
[4]須賀一彦,CRAFT T J,LACOVIDESH.汎用的な解析的壁関数モデル(第1報、滑面~粗面乱流に対応した流れ場のモデル)[C]//日本機械学会論文集B編.东京,2005.
KAZUHIKO S,CRAFT T J,LACOVIDESH,et al.A generalized analytical wall-function for turbulence(1st Report,a flow field model for smooth and rough wall turbulence)[C]//The Japanese Society of Mechanical Engineers.Tokyo,2005.
[5]CRAFT T J,GERASIMOV A V,LACOVIDESH,et al.Progress in the generalization of wall-function treatments[J].International Journal of Heat Fluid Flow,2002,23:148-160.
[6]吴利红,俞建成,封锡盛.水下滑翔机器人水动力研究与运动分析[J].船舶工程,2006,28(1):12-16.
WU L H,YU JC,FENG X S.Hydrodynamic research and motion analysis of AUG[J].Ship Engineering,2006,28(1):12-16.
[7]熊耀宇,段宏,姜治芳,等.数值模拟现代水面舰船带自由面的湍流绕流场[J].中国舰船研究,2010,5(6):16-20,32.
XIONG Y Y,DUAN H,JIANG Z F,et al.Numerical simulation ofmodern surface ship in free surface turbulence flow[J].Chinese Journal of Ship Research,2010,5(6):16-20,32.
[8]REN H L,LIUW X.Calculation ofhydrodynam ic coefficients of floating body with complex wetted surface[J].Journalof Ship Mechanics,2008,12(3):359-367.
[9]操盛文,吴方良.尺度效应对全附体潜艇阻力数值计算结果的影响[J].中国舰船研究,2009,4(1):33-37,42.
CAO SW,WU F L.Investigation of scaling effects on numerical computation of submarine resistance[J].Chinese Journal of Ship Research,2009,4(1):33-37,42.
[10]王冲,刘巨斌,张志宏,等.水下滑翔机沿纵剖面滑行时水动力特性计算与分析[J].舰船科学技术,2009,31(1):134-136,163.
WANG C,LIU JB,ZHANG Z H,et al.Numerical research on dynamic characteristic of underwater glider when it runs in longitudinal section[J].Ship Science and Technology,2009,31(1):134-136,163.
[11]吴方良,吴晓光,马运义,等.潜艇实艇阻力预报方法研究[J].中国舰船研究,2009,4(3),28-32.
WU F L,WU XG,MA Y Y,etal.Method of predicting the total submerged resistance of submarines[J].Chinese Journal of Ship Research,2009,4(3):28-32.
[12]罗寅,张阿漫,朱永凯,等.结合亚格子模型的Lattice-Boltzmann算法[J].中国舰船研究,2010,5(1):10-13.
LUO Y,ZHANG A M,ZHU Y K,et al.Combination of the Lattice-Boltzmann method and the sub-grid model[J].Chinese Journal of Ship Research,2010,5(1):10-13.
[13]WEBB D C,SIMONETTIP J,JONESC P.SLOCUM:an underwater glider propelled by environmental energy[J].IEEE Journal of Oceanic Engineering,2001,26(4):447-452.

