悬臂梁微小形变电测法实验中的力学结构优化设计

王建元，翟 薇，侯建平，庞述先

（西北工业大学，陕西 西安 710072）

1 悬臂梁微小形变电测法

微小形变的测量是大学物理实验中非常典型的一类综合性实验[1－4]，主要方法有光杠杆法、应变片法、光干涉法等。利用应变片作为测量物体微小形变的传感元件，并且由学生搭建电桥电路来测量应变片的电阻，可以将电学测量方法与经典力学结构的分析结合起来，使得学生不仅学习了应力－应变的材料力学知识，了解了力学研究和工程应用领域的重要传感元件，而且锻炼学生的综合运用能力。

悬臂梁加载后的主应变测量是一种常见的设计，其结构如图1所示。通过在悬臂梁活动端的砝码加载使悬臂梁产生变形，在悬臂梁固定端附近的上表面（A处）粘贴应变片。测量其加载前后的电阻，可以计算出悬臂梁上表面在A处的主应变，即：

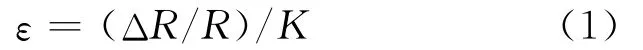
其中，R是加载前应变片电阻，ΔR是加载后的应变片电阻变化量，K为应变片系数。

相对于通过轴向拉伸或压缩的方法产生主应变，悬臂梁活动端加载的方法使得较小的加载重量就可以在固定端附近的上下表面获得较为显著的应变。由于不需要采用几公斤重的巨型砝码，这个实验系统在力学结构设计上更为紧凑，而且操作也更为安全；同时，较大的应变使得应变片的电阻变化较为明显，采用惠斯通单臂电桥结合微调电阻箱即可进行测量。

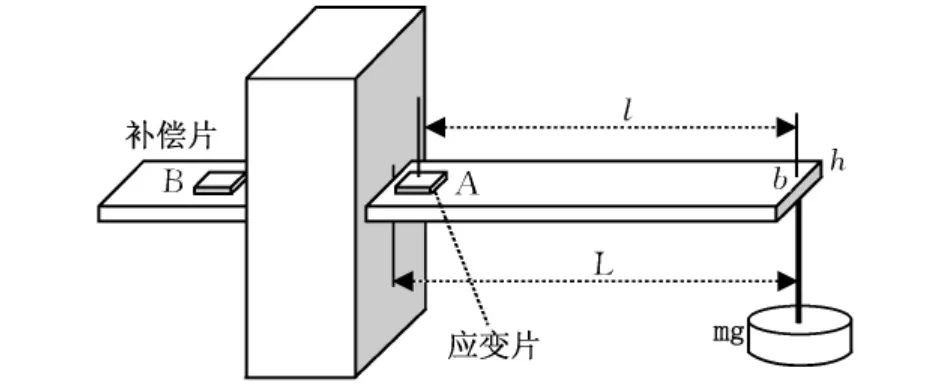
图1 悬臂梁力学结构示意图

最简单的实验设计可以仅要求测量应变（方案1）。如果引入悬臂梁主应变计算公式[5]：

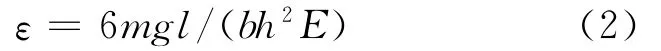
F为悬臂梁活动端垂直加载力，l为悬臂梁末端到应变测试点A的距离，h为悬臂梁厚度，b为悬臂梁截面宽度。结合（1）式，可以得到：

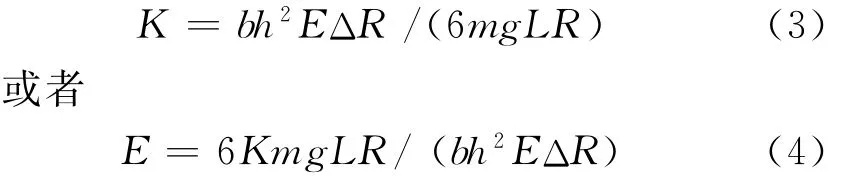
利用式（3），可以通过给定悬臂梁材料的杨氏模量E来间接测量应变片的系数K（方案2）；利用公式（4）可以通过给出应变片的系数K，测量材料的杨氏模量E（方案3）。这3种方案要想实现多次测量，一般采用在悬臂梁活动端逐次增加等重砝码，测量ΔR等间隔变化方法，并采用逐差法处理数据。

2 实验中存在的系统误差

以上实验设计中的测量方法上的系统误差有两个主要来源：

（1）电学测量的系统误差。电路的接通必然带来热量的累积而使得元器件温度升高。应变片和电桥其他桥壁上电阻箱的阻温系数不同，所以各个元器件的电阻值漂移大小不同，这必然造成电桥平衡点的漂移。关于这个系统误差，实验教材[1，4]中的测量电路已经给出了解决的办法。在悬臂梁的反向端设置一个非加载区域，在此区域粘贴另外一个同型号应变片作为补偿片（图1，B处）。测量电路如图2所示，补偿片作为受力应变片的相邻桥臂。这样，两者具有相同的热敏系数，且流过的电流相同，温度变化引起的电阻变化RT相当，电桥的平衡关系实质上就变成：

（Rx＋ΔRT）／（R1＋ΔRT）＝ （Ra＋Rb）／R2＝1 （5）这样就排除了温度对电阻值测量的影响。

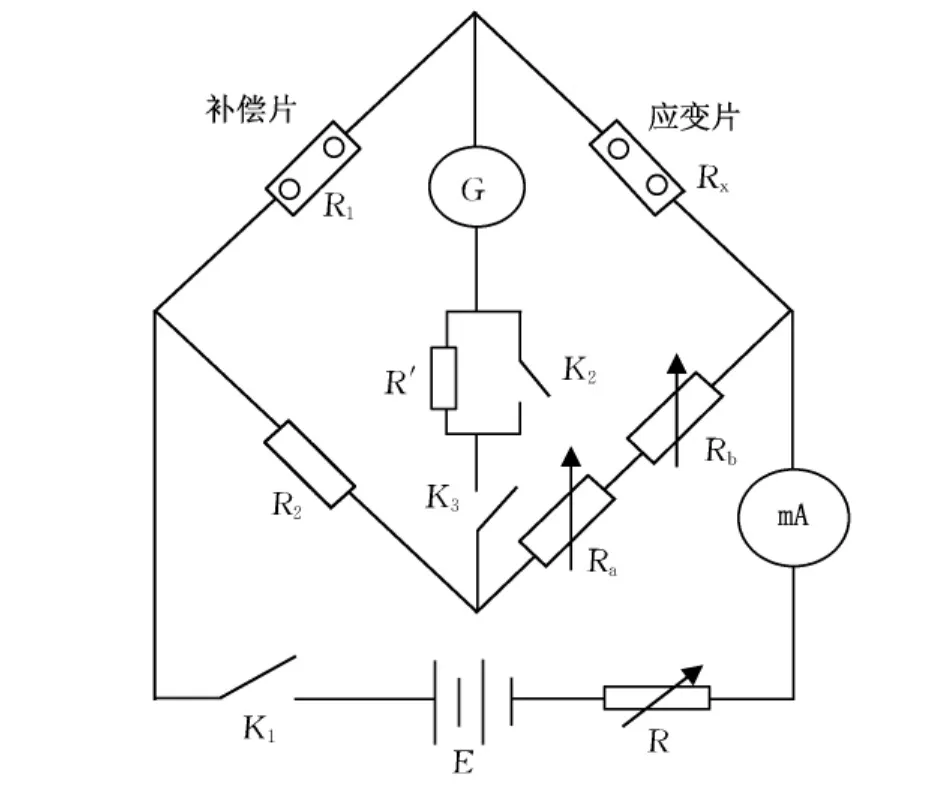
图2 含有温度补偿的测量电路图[1]

（2）力学变形近似引起的系统误差。在进行多个砝码逐次加载进行多次测量的情况下，若忽略加载后悬挂点位置的改变，则所加载砝码的重力垂直于悬臂梁，拉力mg以弯矩M0的形式作用于悬臂梁上，如图3所示。此时没有轴向拉伸力，也就是说完全由弯矩造成了A处的正应力。但是实际加载后，悬臂梁发生显著的弯曲变形，重力不再垂直于悬臂梁。这样，砝码重力分解为轴向的拉力FZ和垂直于轴向的力FM。分力FM对A点产生的弯矩必然小于M0。根据材料力学的常识，对于悬臂梁，同样的力通过轴向拉力作用比通过弯矩作用在A处产生的正应力要小得多。所以可以预测，对于依次加载的多个砝码，悬臂梁的倾斜逐次增大，相同的砝码重力分解出的弯矩就会越小，最终的效果是依次加载的砝码在A处所产生的正应力变化量依次减小。

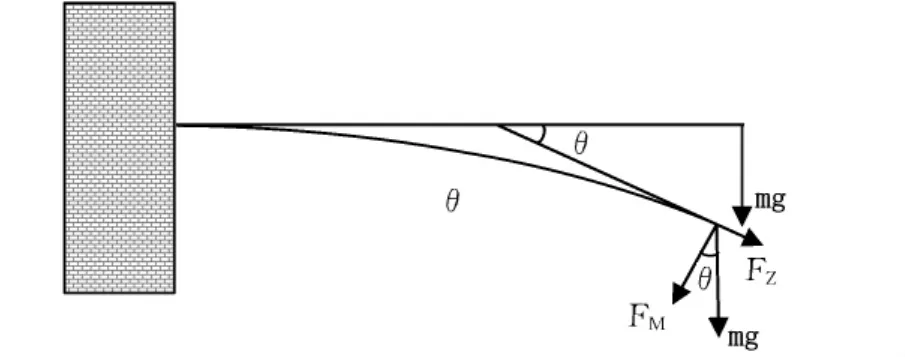
图3 悬臂梁加载变形后的受力分析

大学物理实验的授课对象是所有理工科学生而不是只针对力学专业的学生，本实验的重点是让学生了解应变片的工作原理，掌握微小形变的电测法，另外学习逐差法这个数据处理的重要方法。如果在实验内容上考虑这个专业的力学问题，则会使得实验过于复杂，使得实验难度过高，反而使学生忽略了其中的重点问题。因此，在逐次连续加载的多次测量时，希望应变的衰减足够小，以便近似认为依次加载的砝码在A处产生同样的应力、应变，于是将这一列测量作为等间距多次测量对待。因此，为了更加合理的设计实验，必须进行定量的力学分析计算，讨论这种力学近似造成的系统误差的大小和影响因素，通过优化设计，减小该系统误差。

3 力学变形近似误差的分析测量

悬臂梁弯曲变形后，轴向拉力FZ在A处产生的正应力为：

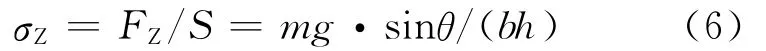
由FM产生的弯矩为：

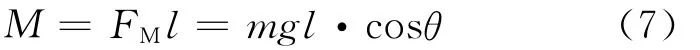
由方形截面悬臂梁的正应力计算公式[6]，可得

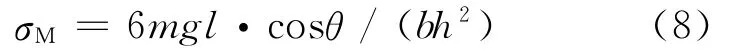
两个正应力的叠加为

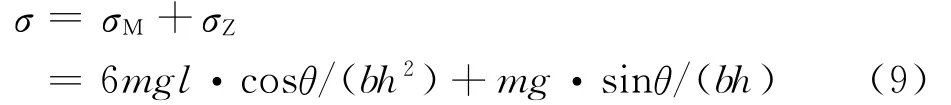
设悬臂梁的杨氏模量为E，则A处的主应变为：

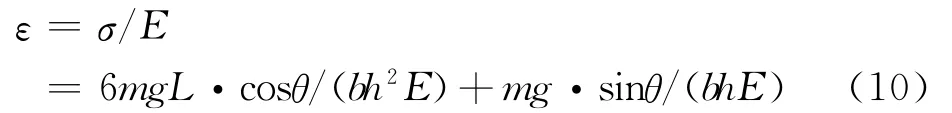
θ＝0的理想状态下，应变为

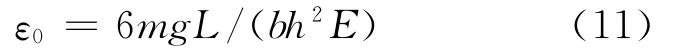
则任意角度下的应变ε与理想值ε0的比值为：

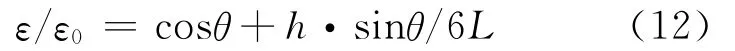
选取一组易变形的薄壁悬臂梁的具体数值，L＝200mm，h＝1mm，带入得：

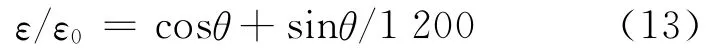
公式（10）的数值关系如图4中实线所示，随着变形角度的增大，同样质量的砝码加载所产生的应变逐渐缩小。θ＝5° 时，ε／ε0＝0.996，衰减很小；θ＝10°时，ε／ε0＝ 0.985；θ ＝ 15° 时，ε／ε0＝0.966，衰减已经非常明显。

图4 不同悬臂梁变形角时，相同砝码加载产生的主应变衰减

在理论计算的基础上，采用L＝200mm，h＝1mm，b＝15mm的薄壁钢材料悬臂梁实际测量了不同加载重量下的末端变形角以及相应的电阻变化量。应变片系数K＝2.25。m为加载重量，θ为悬臂梁变形角，Rx为应变片电阻值，ΔR为相邻Rx的差值，ε／ε0为应变的衰减系数。计算结果如表1所示。

表1 依次加载每50g砝码的实验数据

砝码加载到150g时，变形角达到了5°；而当加载到250g以上时，超过了11°；加载到500g时，变形角超过25°。

在实验教学中采用逐差法处理数据。如果在实验设计上将最大变形角控制在5°以内，则采用前四组Rx数据进行逐差，则有效数字偏少。而采用前6组数据，最大250 g砝码加载重量进行逐差，则逐差结果达到3位有效数字，此时，累积的电阻变化量为0.217Ω，累积的应变为8.02×104。但是，实际的变形角达到了11.25°。

从仪器精度误差的角度出发，必须使每个逐差结果的有效数字至少达到3位；从实验方案的力学结构近似的角度出发，变形角度小于5°为宜，并且越小越好。可以从应变片参数、电桥的电阻测量精度、悬臂梁的结构优化3个方面进行考虑：

（1）电阻应变片的系数。应变片目前主要有金属和半导体两类，金属应变片的灵敏度一般为2左右，而半导体应变片的灵敏度可以达到10以上。但是，半导体应变片最大的缺点是温度稳定性差、灵敏度离散程度大、在较大应变作用下非线性误差大，给使用带来困难，并未广泛应用。

（2）电桥的电阻测量分辨率。在惠斯通单臂电桥的可调桥壁上采用步进值更小的电阻箱，并且提高电桥的灵敏度可以在相同的电阻变化情况下获得更高的测量精度。但是，目前最为常见的通用微调电阻箱步进值为0.001Ω。并且考虑到整个电桥电路各个组件的稳定性和电阻箱接触电阻，不适宜采用更小的微调电阻箱。

（3）悬臂梁的尺寸结构。对于固定的悬臂梁尺寸结构，大的应变必然带来大的变形角。但是不同的悬臂梁尺寸，产生相同的主应变，变形角也是不同的。因此，对其进行结构优化是最为可行和有效的办法。

4 悬臂梁结构尺寸的优化设计

矩形截面悬臂梁末端悬挂加载条件下的变形角公式为[5]：

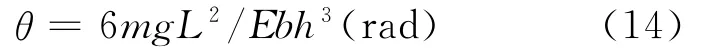
主应变的计算公式（1式）可以变形为：

则变形角可以表示为：

在同样的应ε变下，要想缩小θ，应该增大l，尽量使得l≈L，即应变片的粘贴位置尽量靠近悬臂梁的固定端。则式可以变形为：

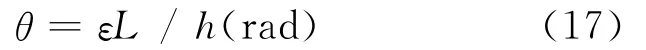
在应变量一定的情况下，增大h或者减小L都可以缩小θ.但是增大h或者减小L都对加载砝码的质量提出了更高的要求，过大的砝码也会给实验带来设计上不便。砝码质量计算公式由（1）式变形为：

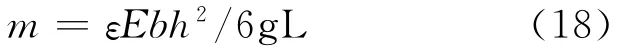
因此必须综合考虑砝码重量m和悬臂梁结构参数h、L的大小。

基于表1测量过程采用的悬臂梁材料和结构参数，进行了增大厚度h，减小长度L的优化设计和计算。考虑到直接测量ΔR的大小，应变取为ε＝1×103，悬臂梁宽度取为b＝15mm，钢的杨氏模量取为E＝1.8×1011Pa，悬臂梁厚度h分别选取1、2、3mm，悬臂梁长度选取为200、150、100mm，变形角计算采用 （17）式，所需砝码质量和变形角的计算结果如表2所示。可以看出，h＝3mm时，L取值为200、150、100mm时变形角均较小，但是所需的m 增大到2.07、2.75、4.14kg，质量较大，不利于桌面实验系统的设计。h＝2mm时，变形角仍然可以接受，L＝100mm时（h组），砝码重量需2.86kg，并且悬臂梁较短，砝码体积较大，影响实验装置的设计；L＝150mm时（e组），所需砝码为1.22kg，变形角4.20°，综合考虑砝码重量m和悬臂梁结构参数h、L的大小，这是一组比较好的组合。

表2 依次加载每50 g砝码的实验数据

5 结束语

“悬臂梁微小形变的电测法”实验是面向理工科学生的大学物理实验课程的重要内容之一。由于课程内容的需要，一般忽略砝码加载后的悬臂梁的变形对测量结果的影响。因此在保证应变量的情况下，必须使得悬臂梁的变形角足够小，同时所需加载重量也不应太大。在采用最常用的应变片（K≈2）以及惠斯通单臂电桥电阻测量分度值一定的情况下（0.001Ω），通过分析计算，合理的选择悬臂梁厚度h，和长度L可以控制变形角小于5°，并且所需砝码的最大重量不足1.5kg，较小的砝码重量也有利于整个系统的紧凑设计。

[1]李恩普，刑凯，曹昌年，等.大学物理实验[M].北京：国防工业出版社，2004.

[2]朱基珍，莫济成，黄榜彪，等.大学物理实验[M].武汉：华中科技大学出版社，2010.

[3]刘跃，张志津，祝威，等.大学物理实验[M].北京：北京大学出版社，2010.

[4]成正维，牛原，张斌，等.大学物理实验[M].北京：北京交通大学出版社，2010.

[5]杜建根.材料力学[M]武汉：武汉理工大学出版社，2008.