孔、裂隙并存地层中的声波测井理论及多极子声场特征

陈雪莲，唐晓明

中国石油大学（华东）地球科学与技术学院，青岛 266555

孔、裂隙并存地层中的声波测井理论及多极子声场特征

陈雪莲，唐晓明

中国石油大学（华东）地球科学与技术学院，青岛 266555

在油、气储层的勘探和开发中观察到的一个现象是储层岩石中普遍存在孔隙和裂隙.随着近年来孔、裂隙介质弹性波动理论的进展，我们可以将此理论应用于测井技术，以此来指导从声波测井中测量孔、裂隙地层的声学参数.本文计算了孔、裂隙地层里充流体井眼中的多极子声场，分析了声场随裂隙介质的两个主要参数（即裂隙密度和裂隙纵横比）的变化特征.井孔声场的数值计算表明裂隙密度可以大幅度地降低井中声波纵、横波的波速和振幅.随着裂隙密度的增加，在测井频段内也可以看到纵、横波速的频散现象（这种频散在孔隙地层中一般是观察不到的）.本文还研究了多极子模式波 （即单极的Stoneley波、伪瑞利波以及偶极的弯曲波）随裂隙参数的变化特征.结果表明，这些模式波的振幅激发和速度频散都受裂隙密度的影响.裂隙密度越高影响越大.此外，裂隙还对模式波的传播造成较大的衰减.相对裂隙密度而言，裂隙纵横比是一个频率控制参数，它控制裂隙对声场影响的频率区间.本文的分析结果对裂缝、孔隙型地层的声波测井具有指导意义.

裂隙，孔隙地层，声波测井，裂隙密度，频散

1 引 言

目前油气勘探和开发的注意力已逐渐转移到非常规油气藏，如致密性地层及蕴藏油气的页岩地层.这些复杂岩性地层的重要特征是低孔、低渗，但裂隙或裂缝比较发育.因此，适应非常规油气藏的勘探需求，研究复杂孔、裂隙地层井孔中的声传播机理及其传播特征具有重要的意义.自20世纪70年代以来，研究者对孔、裂隙介质进行了大量的研究.O′Connel和Budiansky［1］指出裂隙除对介质弹性产生影响外，还会在外力作用下产生一种“挤压喷流”现象，从而使介质呈现黏弹性质，但OB理论没有描述孔隙介质渗透率的影响及与其有关的慢速纵波.Dvorkin和Nur［2］提出了一种Biot理论与挤喷流的统一理论（即BISQ理论）.但BISQ模型在测井频段以下的频域内不成立，慢纵波的衰减在低频时趋于一个很大的值.国内学者针对此理论也展开了进一步研究［3－5］，崔志文、王克协等将 BISQ 理论引入到充液井孔声场的数值计算中，也认识到BISQ理论与Biot理论在低频时的这种巨大差别［6－7］.巴晶针对孔隙分布的不均匀性及其产生的局部流动效应，建立了双重孔隙介质波传播理论，指出双孔波动理论能较好解释岩石内部地震波在中低频带的速度频散现象［8］.唐晓明具体分析孔隙与裂隙之间的挤喷流效应，并将这种效应与描述裂隙的两个重要参数（裂隙密度和裂隙纵横比）联系起来［9］，这里裂隙在三维空间是随机取向的.通过这种联系，把孔隙弹性波动力学和裂隙弹性力学综合，得到了一个可描述孔、裂隙并存的统一弹性波动理论.这一新理论既保持了原有理论的基本特征，又极大地提高了含孔、裂隙介质中弹性波传播的预测和模拟的能力，从而在地球介质的地震和声波测量中有着比原理论更为广泛的应用前景.目前，还未见孔、裂隙并存介质中的声传播规律研究的报道.本文将此理论应用于井孔声场的数值计算，以分析孔、裂隙并存介质井孔中激发的模式波的频散、衰减、灵敏度以及激发强度与裂隙密度之间的关系，并着重研究裂隙参数对多极声源所激发的全波传播特征的影响，研究的结果可以为孔、裂隙并存地层的油气评价以及裂隙参数反演提供理论依据.

2 孔、裂隙并存介质井孔中的声场理论

2.1 孔、裂隙介质弹性波动理论

Biot孔隙介质的应力－位移本构关系可以表为［10］

其中w＝φ（U－u）为孔隙流体位移U相对于固相骨架位移u的相对位移，而

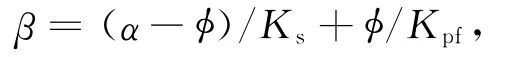
以上各式中的参数为：μ是孔隙介质的剪切模量、且与介质是否干燥或饱和无关，Ks和Kd分别是固相和骨架的体积模量，φ为孔隙度，Kpf为孔隙流体的体积模量.在Biot理论中，充流体介质的体积模量由Gassmann方程给出：

在孔、裂隙并存介质的弹性波传播过程中，除了Biot理论中孔隙流体相对于骨架的整体流动，还包含狭小裂隙和孔隙之间的局部流动.孔、裂隙之间的流体交换，称为挤喷流效应，使得介质的体积模量K变为复数（具体推导见文献［9］）.这意味着介质中又多了一种耗散机制，即挤喷流耗散机制，它使介质中波场的衰减和频散变得较为严重，这时K的表达式为［9］

其中挤喷流效应的贡献可表示为

式中ω为角频率，ε为裂隙密度，γ为裂隙纵横比，η为流体的黏度，v、μ0和K0为没有挤喷流（（S（ω）＝0）时背景介质的泊松比、剪切模量和体积模量，μ0和式（3）中的Kd是裂隙密度的函数，由Thomsen的Biot相恰理论得到［11］，Jn（n＝0，1）是第一类n阶贝赛尔函数.与Gassmann方程中K的表达式（2）相比，多了挤喷流的贡献S（ω）一项.裂隙在三维空间是随机取向时，孔、裂隙并存介质的剪切模量可表示为

引入挤喷流的贡献后干燥和饱和时的μ不再相等，而且μ还是频率的函数.

综上所述，孔、裂隙并存介质弹性波动理论对Biot孔隙波动理论的推广表现在：（1）在弹性模量K和μ中引入了挤喷流的贡献，使之成为频率的函数；（2）将（2）式中的β修正为

2.2 井孔声场的计算

在（r，θ，z）柱坐标中，井孔内声场势函数φn在频率域中的表达式如下：

其中n＝0代表单极源，n＝1代表偶极源，F为井孔内流体的径向波数，r0为偶极距，kz为轴向波数，n＝0时εn＝1，n＞0时εn＝2，第一类n阶贝塞尔函数In代表由井壁向井轴会聚的波，第二类n阶变型贝塞尔函数Kn代表向井外传播的波或发散波，B（ω）为源函数，在全波波形计算时选择瑞克子波的谱函数.

井中的声场由振幅反射系数An确定，而An由井孔与地层的边界条件决定，井壁处流体与地层的径向位移和径向应力连续，井内流体压强与孔、裂隙流体的压强相等［12－13］，且地层在轴向和周向的剪切应力为零，如下式：

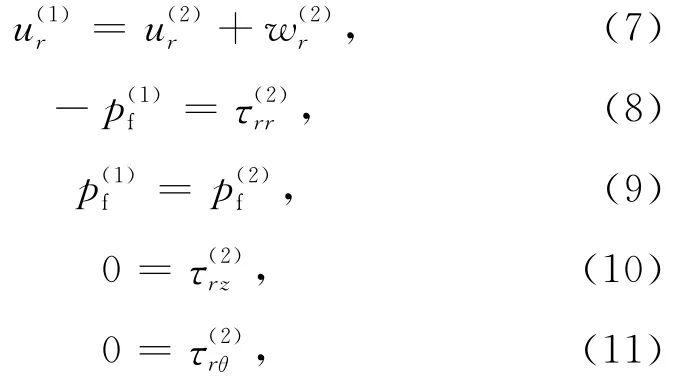
式中τij是井孔外孔、裂隙并存介质中的总应力，上标（1）和（2）分别表示井孔内外的介质，下标f是流体的场量，由上述边界条件得到

An又称为井中声场的响应函数，其中Nn和Dn由边界条件（7）～（11）方程组的系数矩阵决定［12］，将此式带入（6）式可计算井中声场的全波波形.在多极子声场中，模式波往往是全波中的主要成份，它们的贡献来源于An中的极点，而极点的kz值可由频散方程Dn（kz，ω）＝0决定.将（6）式中沿实kz轴的积分由绕极点的留数来表示，就得到了模式波所对应的声场［12－13］.

本文进一步讨论了由频散方程Dn（kz，ω）＝0得到的井孔伪瑞利波、斯通利波以及偶极弯曲波等模式波对地层中的孔、裂隙参数的灵敏度.模式波的相速度和衰减可由模式波极点所对应的波数kz得到，

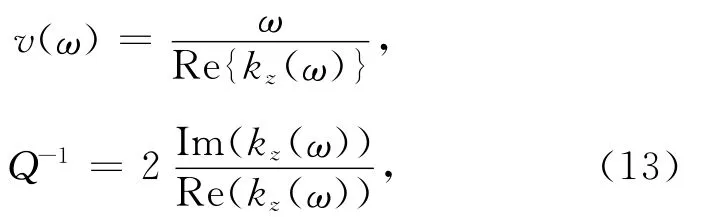
模式波的相速度和衰减对地层参数x的灵敏度为［10］

其中，Sensitivity为灵敏度系数（也称为分配系数），x代表井孔或地层的某参数值.灵敏度可以用来观察某参数在不同频率下对模式波的相速度（或衰减系数）的影响程度.

3 孔、裂隙并存介质声场的数值计算结果及讨论

为了考察地层孔隙度对孔、裂隙并存地层中挤喷流的影响，数值计算时选取了低孔隙度和高孔隙度地层展开研究，具体的地层参数见表1，裂隙密度和纵横比γ的默认值分别是0.15和0.001.井眼半径为0.1m，井内流体的声速和密度分别为1500 m/s和1000kg/m3.

3.1 无限大地层弹性波的频散和衰减特征

表1 含裂隙的高孔隙度和低孔隙度地层参数表Table 1 Parameters of the high porosity and low porosity formation with cracks

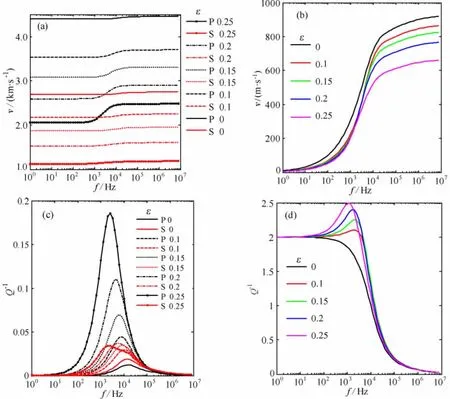
图1 不同裂隙密度下弹性波的频散和衰减（a）和（c）中黑色曲线：快纵波，红色曲线：横波.Fig.1 Elastic wave dispersion and attenuation curves for different crack density values In（a）and（c），black curves are for fast compressional waves and red curves are for shear waves.

图1是高孔隙度地层不同裂隙密度下快纵波、横波以及慢纵波的频散和衰减曲线，裂隙纵横比为0.001.随着裂隙密度的增加，弹性波的相速度均明显的逐渐减小、衰减逐渐增大，衰减峰值和频散显著的频段由高频向低频方向有所偏移（挤喷流耗散效应的中心频率稍有降低）；在裂隙密度为0.25时地层的横波速度已小于井内流体的速度.图2是低孔隙度地层不同裂隙纵横比下快纵波、横波以及慢纵波的频散和衰减曲线，裂隙密度为0.25.随着裂隙纵横比的增加，频散最明显或衰减峰值所在的频段明显地向高频方向偏移（即纵横比的增加降低了裂隙向孔隙挤喷流动所需的时间），衰减极值稍有降低，这在慢纵波的衰减变化图上体现的最明显（同一裂隙密度下随裂隙纵横比的增大，声扰动引起的裂隙受挤压力减小，挤喷流量降低）.在裂隙纵横比从0.0001变到0.001时高频和低频时的纵横波速度稍有降低，但在裂隙纵横比达到0.01时，弹性波的速度降低明显，这与裂隙纵横比较大时，裂隙孔隙度对总孔隙度的贡献不可忽略，致使岩石的弹性模量进一步降低有关.

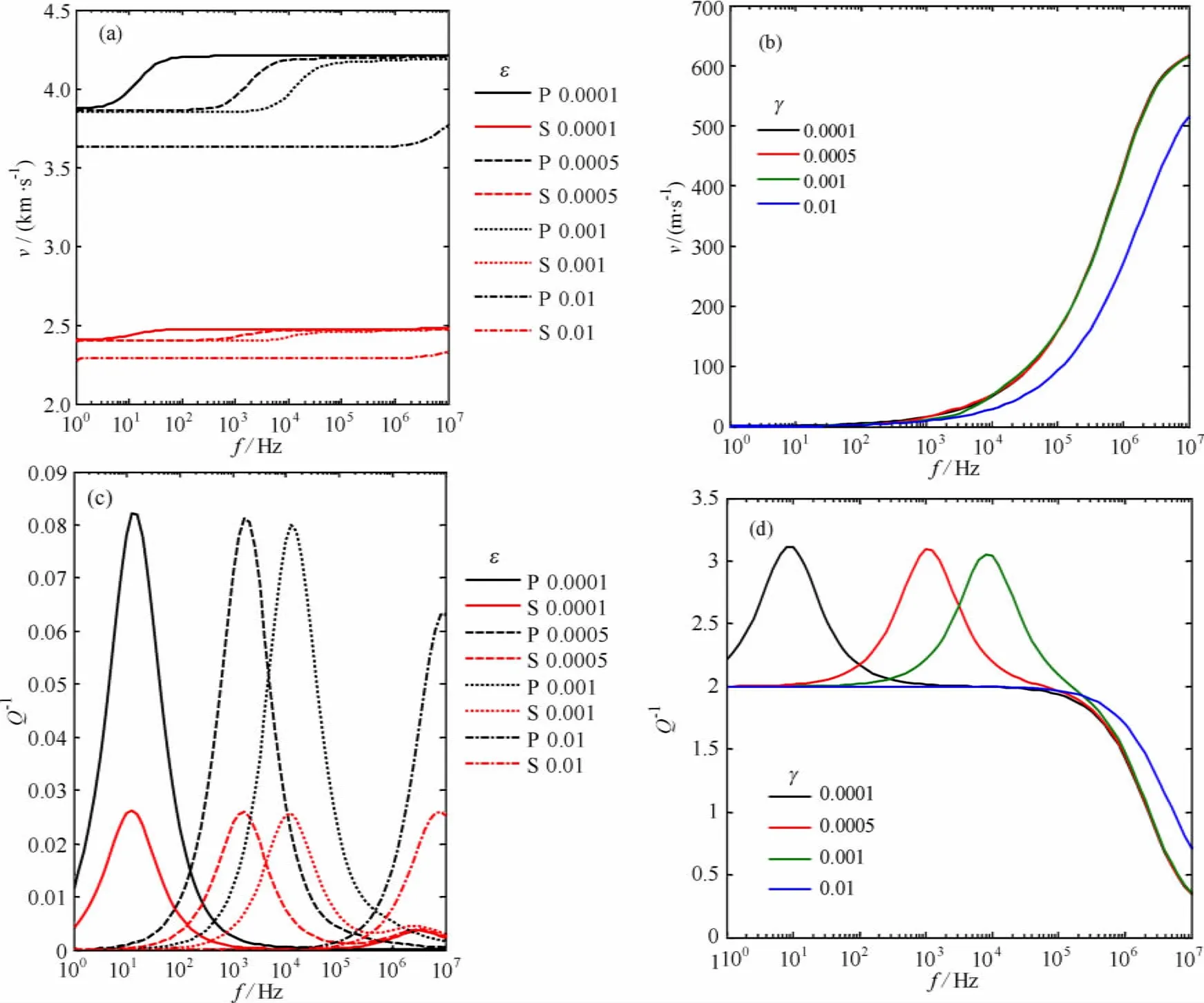
图2 不同裂隙纵横比下弹性波的频散和衰减（a）和（c）中黑色曲线：快纵波，红色曲线：横波Fig.2 Elastic wave dispersion and attenuation curves for different crack aspect ratio values In（a）and（c），black curves are for fast compressional waves and red curves are for shear waves

3.2 充液井孔中的声传播特征

3.2.1 低孔隙度时孔、裂隙并存地层充液井孔中的声传播特征

图3是地层孔隙度和渗透率较低时，不同裂隙密度下充液井孔中单极子声源激发的斯通利波和偶极子声源激发的弯曲波的频散、衰减以及灵敏度曲线，计算参数见表1.在低孔隙度地层裂隙密度从0变到0.25时，斯通利波的相速度逐渐减小（图3a），由于弯曲波的低频速度受地层的横波速度影响大，在裂隙密度由0变到0.25时，在截止频率附近，弯曲波的相速度降低较斯通利波明显（图3b）.斯通利波和弯曲波的衰减均随着裂隙密度的增加逐渐增大.从灵敏度曲线上可以看出裂隙密度越大，斯通利波和弯曲波的相速度和衰减对其灵敏度越高；模式波的相速度对裂隙密度的灵敏度在低频段大于高频段，这与硬地层斯通利波和弯曲波随着频率的增加逐渐趋于井孔流体速度有直接关系，即高频段模式波对井孔流体速度更敏感；由于低频时孔隙流体中的黏滞力起主要作用，斯通利波的衰减在低频段对裂隙密度的灵敏度也较小，随着频率的增加，孔隙中流体的惯性力起重要作用，灵敏度又逐渐增大；弯曲波的衰减对裂隙密度的灵敏度在截止频率附近最大，随着频率的增加逐渐减小，在艾里相处减小最明显，频率再继续增大，灵敏度变化不大.对比斯通利波和弯曲波的频散和衰减的变化程度可知，在现有测井仪器的工作频段弯曲波受裂隙的影响程度较大.

图3 斯通利波（a）和弯曲波（b）的频散、衰减及对裂隙密度的灵敏度SFig.3 The sensitivity coefficients of Stoneley wave（a）and flexural wave（b）to crack density

图4 斯通利波（a）和弯曲波（b）的激发强度EFig.4 Stoneley（a）and the flexural（b）wave excitation as a function of frequency

图4是斯通利波和弯曲波的激发强度曲线，随着裂隙密度的增大斯通利波的激发强度逐渐减弱；弯曲波的激发强度在截止频率附近随裂隙密度的增加逐渐增大，这在偶极全波模拟时也得到了体现，在艾里相附近变化趋势恰好相反.

图5是伪瑞利波的频散、衰减和激发强度曲线.随着裂隙密度增加艾里相所处的频段向高频方向偏移，其相速度和截止频率附近的群速度逐渐降低，在艾里相附近群速度变化趋势正好相反，随着裂隙密度的增加群速度逐渐增大，且群速度值小于井内流体速度；随着裂隙密度的增加伪瑞利波的衰减逐渐增大；伪瑞利波的激发强度在截止频率附近随裂隙密度的增加稍有增大，艾里相附近随着裂隙密度的增加逐渐减小.伪瑞利波的频散、衰减以及激发强度的变化规律与弯曲波类似.

图6是充液井孔中单极子和偶极子声源激发的全波波形.单极子声源激发主频分别为3kHz、8kHz和12kHz，全波模拟结果显示，随着裂隙密度变大单极全波中的纵横波速度明显减小（图6（c，e）），幅度逐渐降低.可见，含裂隙地层，可使低孔隙度下的岩石声速很低，声速和孔隙度之间的相关性降低，若利用威利时间平均公式估算地层孔隙度会有较大偏差.随裂隙密度增大，斯通利波速度稍有降低，幅度逐渐减小，在高频激发时幅度降低较明显，这与图3a显示的在高频段斯通利波的衰减对裂隙较敏感一致.伪瑞利波随裂隙密度的增加幅度逐渐减低 （图6c），这与此频段下的激发强度随裂隙密度增大而逐渐减小、衰减随裂隙密度增大而增大有直接关系（图5（b，c）），伪瑞利波的波包传播速度随裂隙密度增加有增大的趋势，这与此激发频段的伪瑞利波的群速度随裂隙密度增加逐渐增大相吻合（图5a）.

图5 伪瑞利波的频散（a）、衰减（b）和激发强度（c）曲线Fig.5 The dispersion（a），attenuation（b），and excitation（c）curves of the pseudo－Rayleigh wave

偶极全波波形随裂隙密度变化较复杂，在激发主频为1kHz（主频低于截止频率，但有一定的带宽）时（图6b），随裂隙密度的增加，波形幅度逐渐增大，这与截止频率附近弯曲波的激发强度随裂隙密度的增加而逐渐增大有关（见图4b）.当激发主频增加到3kHz和6kHz时（图6（d，f）），随裂隙密度增加激发强度逐渐减弱以及引起的地层衰减起明显作用，波形幅度基本随裂隙密度增加逐渐降低.

图7a对比了不同裂隙纵横比（裂隙密度是0.25）下的单极全波波形，激发主频为8kHz，图中纵波放大显示.可见，单极全波中的纵横波幅度随着裂隙纵横比从0.0001增大到0.001时减小明显，速度基本不变；在裂隙密度继续增大到0.01时，纵横波幅度又逐渐增大（速度稍有降低），这与裂隙纵横比是0.001时裂隙造成的纵横波衰减峰值所在的频段恰与测井响应频段一致有关；斯通利波幅度与纵横波幅度的变化趋势基本一致，但幅度变化程度相对于纵横波较弱.图7b是激发主频为1.2kHz时的全波，主要成分是斯通利波，由图2可知1.2kHz恰与裂隙纵横比为0.0001时慢纵波的衰减峰值一致，但斯通利波的幅度随裂隙纵横比降低变化不明显，这与低频斯通利波的衰减主要受流体黏滞力影响有关，传播特征不明显（即低频斯通利波的衰减对裂隙不敏感，见图3a）.

综合分析低孔隙度、裂隙并存地层的声传播特征可见，井孔接收的纵横波速度和衰减均明显受裂隙密度的影响，裂隙纵横比主要控制由裂隙造成的声波频散和衰减明显的频段；井孔弯曲波的相速度和衰减在测井频段较斯通利波对裂隙的存在更敏感.

3.2.2 高孔隙度时孔、裂隙并存地层充液井孔中的声传播特征

含裂隙的高孔隙度地层充液井孔中的模式波的频散特征与低孔隙度地层类似，这里就不再赘述.但高孔隙度地层裂隙较发育时使地层的弹性模量明显降低，如表1所列的地层参数下，在裂隙密度为0.25时地层的横波速度已小于井内流体速度，井孔中接收的全波波形体现出软地层的传播特征.图8是单极声源主频分别为8kHz和3kHz时在孔、裂隙并存地层充液井孔中接收的全波波形，源距为3m.随着裂隙密度的增加，纵横波以及斯通利波的速度均逐渐降低、幅度逐渐减小；在裂隙密度为0.25时，地层横波速度已低于井孔流体声速，井孔中接收的泄露纵波幅度逐渐增加，在声源主频较高时（8kHz），泄露纵波的幅度增强明显.

图6 5个裂隙密度下的单极和偶极全波波形Fig.6 Synthetic waveforms excited by the monopole and dipole sources for 5crack density values

图7 不同纵横比下的单极全波波形对比Fig.7 Synthetic waveforms excited by the monopole sources with 4crack aspect ratio values

通过对图8a三个裂隙密度下接收的地层纵波的频散分析（见图9中的离散点曲线）可知，随地层裂隙密度的增加，在地层纵波速度降低的同时，也使其频散变得明显，从4kHz到14kHz，三个裂隙密度下的速度增加量分别为88m/s、120m/s和137m/s.因此，在孔、裂隙并存地层传播的纵波的频散特征已不能忽略，测井频率下测量的纵波速度与岩石物理实验测量得到的纵波速度会有明显差异.与同一裂隙密度下无限大地层快纵波的频散曲线（图9中实线）对比，井孔中接收的地层纵波由于在井壁表面滑行并向井内辐射声波使其速度略低于无限大地层中的快纵波，但两者差别低于1%.

图8 不同裂隙密度下单极声源激发的全波Fig.8 The full waveforms excited by the monopole source

图9 井孔中接收的地层纵波（离散点）和地层中快纵波（实线）的频散曲线Fig.9 Comparison of dispersion data from compressional wave along borehole （markers）and dispersion （solid curve）for an unbounded formation

图10 不同裂隙密度下弯曲波的全波波形（a）及频谱（b）Fig.10 Full waveforms（a）excited by the dipole source and amplitude spectrum （b）for different crack density values

图10是偶极子声源主频为3kHz时在孔、裂隙并存地层充液井孔中激发的全波波形及其频谱，源距为3m.全波特征与低孔隙度时的类似，从激发主频为3kHz时接收的波形频谱（（图10d）中也可看出，裂隙的存在使得波形中的低频成分增强，高频成分减弱.

基于孔隙地层Biot理论的数值计算结果表明，井孔中的斯通利波和弯曲波的衰减均对地层渗透率较敏感［14］.孔隙流体的流动会对斯通利波沿井传播的能量产生衰减.井孔中斯通利波和地层渗透率的相互作用，是由孔隙流体中慢纵波的激发和传播造成的.地层裂隙的存在，使得孔隙流体中的慢纵波速度减小，衰减增大.图11考察了斯通利波相速度和衰减对裂隙密度和渗透率的灵敏度，裂隙密度固定为0.15不变，在渗透率的三个基值（100mD、10mD和1mD）下，斯通利波的相速度对裂隙密度的灵敏度均明显高于对渗透率的灵敏度，但斯通利波的衰减在渗透率基值较大或低频时，对地层渗透率的敏感性大于对裂隙密度的灵敏度，因此在孔、裂隙并存地层建议利用低频斯通利波的衰减估算地层渗透率.

图11 斯通利波相速度（a）和衰减（b）对裂隙密度和渗透率的灵敏度Fig.11 The sensitivity coefficients of Stoneley wave phase velocity（a）and attenuation（b）to crack density and permeability

图12 弯曲波的相速度（a）和衰减（b）对裂隙密度和渗透率的灵敏度对比Fig.12 The sensitivity coefficients of the phase velocity（a）and attenuation（b）of the flexural wave to crack density and permeability

图12是弯曲波的相速度和衰减对孔、裂隙并存介质中的裂隙密度和渗透率的灵敏度对比图.弯曲波的相速度对裂隙密度的敏感性远远大于对渗透率的灵敏度；在裂隙密度较大（0.15和2.5）时，弯曲波的衰减对裂隙密度的灵敏度也明显高于渗透率，这种现象在低频段（现有仪器的偶极子声源的工作频段）尤为突出.可见在含孔、裂隙地层弯曲波的相速度和衰减均受裂隙的影响较大，随着裂隙发育越强，弯曲波对渗透率的敏感性越小，因此利用弯曲波衰减估算得到的地层渗透率的可靠性在含裂隙地层下降；综合分析弯曲波的频散、衰减以及灵敏度曲线可见，若应用弯曲波信息反演裂隙参数时应优先选择低频弯曲波信息.对比图11和图12与图3可见，同一裂隙密度和纵横比下，低孔隙度地层井孔模式波的相速度和衰减对裂隙密度的灵敏度较高孔隙度地层的低一些.

4 结 论

通过对含孔、裂隙并存地层井孔模式波的频散、衰减、激发强度以及井孔全波的数值计算，分析了裂隙的两个重要参数，即裂隙密度和裂隙纵横比，对斯通利波、伪瑞利波、弯曲波以及井孔中接收的地层纵横波传播的影响，得到以下主要结论：

（1）随着地层中裂隙密度的增加，弹性波的速度逐渐减小，衰减增大，且快纵波和横波的频散较孔隙地层变得明显；随着裂隙纵横比的增加，弹性波频散最严重和衰减峰值所在的频率，由低频向高频方向移动，但对弹性波的速度变化量和衰减峰值影响不大.

（2）从单极全波模拟结果可知，地层中裂隙的存在，使得井孔中接收的纵波、横波速度变小、频散明显且衰减变大，此变化规律与无限大地层中的弹性波规律一致；由于裂隙造成的孔隙度相对较小，而使声速明显减小，因此，声速和孔隙度之间的相关性降低，在利用威利时间平均公式估算地层孔隙度时会造成较大偏差.

（3）通过对斯通利波频散、衰减的数值计算结果分析可知，低频斯通利波的传播速度受裂隙影响较大，随裂隙密度的增加相速度逐渐减小；斯通利波的衰减因裂隙的存在有所增加，但低频时流体的黏滞力起主要作用，其衰减受裂隙密度的影响相对较小，且低频段斯通利波的衰减对裂隙密度的灵敏度低于对渗透率的灵敏度，因此在孔、裂隙并存地层利用低频斯通利波的衰减估算地层的渗透率较可靠.

（4）从弯曲波的频散、衰减以及灵敏度曲线的变化趋势可知，由于弯曲波的低频速度受地层横波速度的影响最大，裂隙的存在明显降低了地层的横波速度，弯曲波的相速度随裂隙密度的增加逐渐减小，但在艾里相附近弯曲波的群速度随裂隙密度的增大稍有增大，这在偶极全波波形中也有体现；弯曲波的衰减随裂隙密度的增加逐渐增大；艾里相附近随裂隙密度的增加激发强度逐渐减弱，但在截止频率附近的激发强度随裂隙密度增加稍有增大，因此在不同主频的声源激发下弯曲波波形幅度随裂隙密度的变化趋势不一致；从灵敏度曲线上可知弯曲波的相速度对裂隙密度的灵敏度较其衰减大，弯曲波的相速度和衰减对裂隙的灵敏度均比斯通利波大，可见裂隙的存在对弯曲波的影响比斯通利波明显.

（5）裂隙在低孔隙度地层对全波波形的影响程度小于高孔隙度地层，但均造成了明显的纵波和横波速度的降低和幅度衰减，井孔中模式波的速度和衰减也受到了裂隙影响，但影响程度和规律性较纵波和横波差，因此在下一步反演地层裂隙参数时可选择声波（纵横波）速度和衰减（频率的函数）联合反演裂隙密度和裂隙纵横比.

（References）

［1］ O′Connell R J.A viscoelastic model of anelasticity of fluid saturated porous rocks.∥Physics and Chemistry of Porous Media，AIP Conf.Proceedings，1984：166－175.

［2］ Dvorkin J，Nur A.Dynamic poroelasticity：A unified model with the squirt and the Biot mechanisms.Geophysics，1993，58（4）：524－533.

［3］ 杨顶辉.孔隙各向异性介质中基于BISQ模型的弹性波传播理论及有限元方法.北京：石油大学，1998.Yang D H.Theory of Propagation of Elastic Waves Based on the BISQ Model and Finite Element Method in Porous Anisotropic Media（in Chinese）.Beijing：Petroleum University，1998.

［4］ Cheng Y F，Yang D H，Yang H Z.Biot/Squirt model in viscoelastic porous media.Chin.Phy.Lett.，2002，19（3）：445－448.

［5］ 孟庆生，何樵登，朱建伟等.基于BISQ模型双相各向同性介质中地震波数值模拟.吉林大学学报 （地球科学版），2003，33（2）：217－221.Meng Q S，He J D，Zhu J W，et al.Seismic modeling in isotropic porous media based on Bisq model.Journal of Jilin University （Earth Science）（in Chinese），2003，33（2）：217－221.

［6］ 崔志文.多孔介质声学模型与多极源声电效应测井和多极随钻声测井的理论与数值研究［博士论文］.长春：吉林大学，2004.Cui Z W.Theoretical and numerical study of modified Biot′s models，acous to electric well logging and acoustic logging while drilling excited by multipole acoustic source［Ph.D.thesis］（in Chinese）.Changchun：Jilin University，2004.

［7］ 崔志文，王克协，曹正良等.多孔介质BISQ模型中的慢纵波.物理学报，2004，53（9）：3084－3089.Cui Z W，Wang K X，Cao Z L，et al.Slow waves propagation in BISQ poroelastic model.Acta Physica Sinica（in Chinese），2004，53（9）：3084－3089.

［8］ 巴晶.双重孔隙介质波传播理论与地震响应实验分析.中国科学：物理学 力学 天文学，2010，40（11）：1－12.Ba J.Wave propagation theory in double－porosity medium and experimental analysis on seismic responses.ScientiaSinica （Physica，Mechanica ＆ Astronomica）（in Chinese），2010，40（11）：1－12.

［9］ 唐晓明.含孔隙、裂隙介质弹性波动的统一理论－Biot理论的推广.中国科学：地球科学，2011，41（6）：784－795.Tang X M.A unified theory for elastic wave propagation through porous media containing cracks：An extension of Biot′s poroelastic wave theory.Science China Earth Sciences（in Chinese），2011，41（6）：784－795.

［10］唐晓明、郑传汉.定量测井声学.北京：石油工业出版社，2004：20－39.Tang X M，Zheng C H.Quantitative Borehole Acoustic Methods（in Chinese）.Beijing：Petroleum Industry Press，2004.

［11］ Thomsen L.Biot－consistent elastic moduli of porous rocks：Low－frequency limit.Geophysics，1985，50（12）：2797－2807.

［12］ 张碧星，王克协，董庆德.双相介质井孔多极源声测井理论及分波分析与全波计算.地球物理学报，1995，38（S1）：178－192.Zhang B X，Wang K X，Dong Q D.Theory of acoustic multipole logging and analysis of wave components and calculation of full waveforms for two－phase medium formation.Chinese J.Geophys.（in Chinese），1995，38（S1）：178－192.

［13］ 张海澜，王秀明，张碧星.井孔中的声场和波.北京：科学出版社，2004.Zhang H L，Wang X M，Zhang B X.Acoustic Field and Waves in Borehole （in Chinese）.Beijing：Science Press，2004.

［14］ 陈雪莲，王瑞甲.径向分层TI孔隙介质井孔中激发的模式波的数值研究.地球物理学报，2008，51（4）：1270－1277.Chen X L，Wang R J.A numerical study on the mode waves excited by the multipole sources in the fluid－filled borehole embedded in radially layered transversely isotropic porous medium.Chinese J.Geophys.（in Chinese），2008，51（4）：1270－1277.

（本文编辑 胡素芳）

Numerical study on the characteristics of acoustic logging response
in the fluid－filled borehole embedded in crack－porous medium

CHEN Xue－Lian，TANG Xiao－Ming

School of Geosciences ＆Technology，China University of Petroleum，Qingdao 266555，China

In the exploration and development of hydrocarbon reservoirs，a common observation is the universal presence of cracks and pores in formation rocks.With the recent development of elastic wave theory for the cracked porous rock，it is now possible to utilize the theory as a foundation for measuring elastic properties of such rocks using acoustic logging.We have implemented the theory to calculate the multipole acoustic propagation in the fluid－filled borehole.The acoustic wave characteristics are studied for two controlling parameters of the cracked rock，namely crack density and crack aspect ratio.The calculated full waveforms show that cracks significantly reduce the velocity and amplitude of compressional and shear waves.With the increase of crack density，the dispersion of compressional and shear waves，which is insignificant for a poroelastic formation，can even be observed in the logging frequency range.The borehole guided waves，i.e.，the monopole Stoneley wave，pseudo－Rayleigh wave，and the dipole flexural wave are analyzed in connection with the crack parameters.The results show that both the velocity dispersion and wave amplitude excitation characteristics of these guided modes are significantly affected by the presence of cracks.The cracks also induce significant attenuation of the waves along the borehole.The effects become pronounced with the increase of cracks density.In comparison，the crack aspect ratio parameter controls mainly the frequency band where these effects occur.The analysis results can be used to provide a guideline for acoustic logging in cracked/fractured formations.

Crack，Porous medium，Acoustic logging，Crack density，Dispersion

10.6038/j.issn.0001－5733.2012.06.035

P631

2011－10－05，2012－03－28收修定稿

陈雪莲，唐晓明.孔、裂隙并存地层中的声波测井理论及多极子声场特征.地球物理学报，2012，55（6）：2129－2140，

10.6038/j.issn.0001－5733.2012.06.035.

Chen X L，Tang X M.Numerical study on the characteristics of acoustic logging response in the fluid－filled borehole embedded in crack－porous medium.ChineseJ.Geophys.（in Chinese），2012，55（6）：2129－2140，doi：10.6038/j.issn.0001－5733.2012.06.035.

国家自然科学基金（41174088）和国家青年自然科学基金（40804020）项目，中央高校基本科研业务费专项资金（10CX04007A）资助.

陈雪莲，女，1976生，副教授，2006年获中国石油大学（华东）地质资源与地质工程专业博士学位，主要从事声波测井方法及岩石物理的教学和科研工作.E－mail：chenxl@upc.edu.cn