证据理论在汽轮机转子故障诊断中的应用

程加堂 艾 莉 徐绍坤

(红河学院工学院，云南 蒙自 661199)

0 引言

汽轮机组是一个集机、电、液于一体的复杂系统，它是电力工业中的关键设备。降低汽轮机组的故障，提高其可靠性是保证电力系统安全运行的前提。作为整个系统的核心部分，汽轮机转子在长期连续高速的旋转过程中，将不可避免地出现故障。因此，研究汽轮机转子的故障诊断技术具有重要的现实意义。

由于在某些故障征兆下，各个故障都有一定的发生概率。通过信息融合，将发生概率最大的判定为主要故障，可提高诊断精度，所以证据理论特别适合处理信息融合的故障诊断问题[1]。因此，研究人员将证据理论应用于直流电机及航空发动机的故障诊断中[2－3]，取得了较好效果。

本文利用灰色神经网络对汽轮机转子进行局部故障诊断，并将诊断结果作为证据体。根据证据理论[4－7]，对各证据体进行合成，并计算它们的基本可信任分配函数，从而判定故障类型。

1 证据理论

1.1 基本概念

设Θ表示有限个证据信息X所有可能结果组成的集合，且集合内的元素相互独立，则称Θ为X的识别框架。Θ中的所有可能的集合用幂集2Θ表示。若集函数 m：2Θ→[0，1]，且满足：

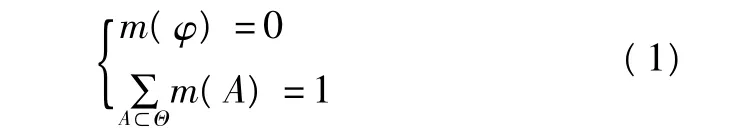
则称m为辨识框架Θ上的基本可信任分配函数，m(A)为A的基本概率赋值，它表示对命题A的精确信任程度。

如果A为Θ的子集，且m(A)＞0，则称A为证据的焦元，所有焦元的集合称为核，证据由证据体[m，m(A)]组成。

由基本可信任分配函数，可定义相应的信任函数和似真度函数为：

式中：Bel(A)表示A为Θ的信任函数，信任函数又称下限函数，表示对A的总信任度;似真度函数Pl(A)也称为上限函数，表示不否定命题A的程度或者说发现A可靠或似真的程度;A的不确定性由u(A)=Pl(A)－Bel(A)来表示，置信区间为[Bel(A)，Pl(A)]，表示对A的不确定区间。

1.2 组合规则

设Bel1和Bel2是同一识别框架Θ上的两个信任函数，m1和m2分别是其对应的基本可信任分配函数，焦元分别为 A1，A2，…，Am与 B1，B2，…，Bn，并且：

式中：i=1，2，…，m;j=1，2，…，n。

此时，m1和m2可以组成一个新的基本可信任分配函数m=m1⊕m2，相应的信任函数用(Bel1⊕Bel2)表示，信任函数的大小可通过(m1⊕m2)来计算 。这时，合成后的基本可信度分配函数为：

式中：k为证据间的冲突程度。当k≠1时，m(C)有一个确定的概率赋值;否则，认为m1与m2矛盾，不能对它们进行组合。对于多个证据的组合情况，需要逐个进行两两组合。此外，由组合所获得的最终证据与组合时的次序无关。

2 证据理论融合算法

2.1 灰色神经网络

灰色神经网络是指将灰色系统理论和神经网络相结合的一种算法，目的是使两者优势互补，更好地解决复杂的不确定性问题。其建模的思路为：先用灰色建模方法进行累加处理，使原始数据序列呈单调增长趋势，以便神经网络进行逼近;再基于BP网络建立对象的预测模型;最后经累减还原后即得预测值。这种方法发挥了灰色模型中累加生成的优点，增强了原始数据序列的规律性，提高了系统建模的效率与模型的精度。从结构上看，两者的结合为“串联”型。该模型又可称作串联灰色神经网络模型[8]。

2.2 算法实现流程

汽轮机转子的故障类型复杂多样，具有渐变和不规则性。如果仅仅从某一方面进行故障诊断，结果往往不完备。为此，本文采用证据理论混合算法的故障诊断方法，充分利用传感器信息，提高了故障诊断准确度。故障诊断系统的流程如图1所示[9]。

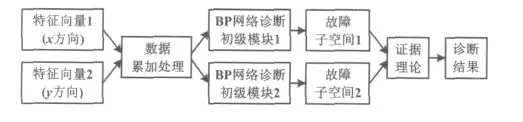
图1 故障诊断流程图Fig.1 Flowchart of fault diagnosis

3 算法应用实例

3.1 特征量提取

汽轮机是大型的旋转机械，振动信号是其非常重要的特征信号。因此，汽轮机转子的故障诊断总是从振动信号入手，并从中提取故障征兆，从而建立故障征兆集合与故障集合的映射关系。

选取汽轮机转子常见的4种故障类型，即不平衡、不对中、碰磨、松动(分别用 y1、y2、y3、y4表示)作为故障识别框架，并在局部故障诊断中定义故障类型的编码为：不平衡(1 0 0 0)、不对中(0 1 0 0)、碰磨(0 0 1 0)、松动(0 0 0 1)。在发生这些故障征兆的基础上，选取x方向、y方向的8种故障特征参数，即(0 ～0.375)f、(0.375 ～ 0.75)f、(0.75 ～ 0.937 5)f、(0.937 5 ～ 1.125)f、(1.125 ～ 1.5)f、(1.5 ～ 3.0)f、(3.0 ～5.0)f、＞5.0f(其中 f为基频)作为该识别框架的证据体[10]，分别用 x1，x2，…，x8表示。部分样本故障数据如表1所示。

表1 部分样本故障数据Tab.1 Part of the sample data

3.2 局部故障诊断

对各个传感器检测的振动信号进行特征提取，并经过归一化及累加生成处理后，分别作为2个并行的BP神经网络的输入样本。训练后的网络输出经过累减还原后，即为局部故障诊断结果。试验中，子网结构均为8 －12 －4，训练目标为 0.000 1，置信门限设为 0.9。下面以汽轮机转子不平衡故障为例，具体说明该故障诊断方法的有效性，网络输出如表2所示。

表2 输出结果比较Tab.2 Comparison of outputs

根据所定义的故障编码规则可知，在x和y方向上，出现不平衡故障的概率最高。因此，采用灰色建模方法对数据进行相应处理后得到的数据与单纯采用BP神经网络相比，其诊断结果更接近期望值。

3.3 决策故障诊断

对子网输出进行归一化处理，再对可能出现的不平衡、不对中故障进行证据组合后，得到的不同子网络的可信度分配如表3所示。

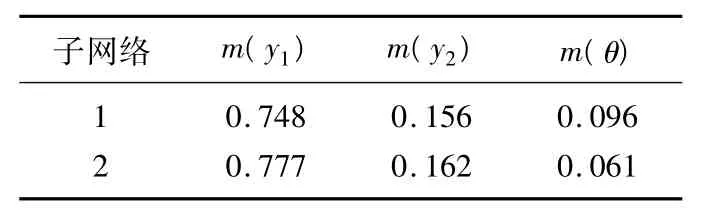
表3 可信度分配Tab.3 Credibility distribution

表3中，m(y1)表示对故障y1的信任度，m(y2)表示对故障y2的信任度，m(θ)表示故障类型的不确定度。此时，2个子网络故障诊断的可信度值均小于0.9，对于是否出现不对中故障尚不能完全排除。当k=0.242 39时，子网络融合后的故障可信度分配如表4所示。

表4 融合结果Tab.4 Fusion results

比较表3与表4可知，融合后发生不平衡故障y1的可信度值提高，达到0.925 8，大于置信门限0.9。同时，不对中故障y2的可信度下降到0.066 4。此外，不确定度值也大幅下降到0.007 73，说明融合后故障诊断的准确性增强。此时可以确定所发生的故障类型为不平衡故障，与实际发生的故障类型相吻合。

为了评估该诊断方法的性能，分别取不同故障模式下的典型样本进行测试，置信门限仍设为0.9，结果如表5所示。

表5 典型样本诊断结果Tab.5 Diagnosis results of typical samples

从表5典型样本诊断结果可以看出，该方法提高了故障诊断的准确率。

4 结束语

对汽轮机转子的故障进行诊断，将故障特征量转化为证据推理问题。在采用灰色神经网络进行局部故障诊断的基础上，按照证据合成规则，实现了汽轮机转子故障诊断的最优决策。该方法有效地提高了正判率，降低了诊断的不确定性。

[1]李巍华，张盛刚.基于改进证据理论及多神经网络融合的故障分类[J].机械工程学报，2010，46(9)：93 －99.

[2]嵇斗，王向军.基于D-S证据理论的直流电机故障诊断研究[J].电机与控制应用，2008，35(2)：49 －51.

[3]杨建平，黄洪钟.基于证据理论的航空发动机早期故障诊断方法[J].航空动力学报，2008，23(12)：2327 －2331.

[4]梁旭荣，姚佩阳，梁德磊.改进的证据组合规则及其在融合目标识别中的应用[J].电光与控制，2008，15(12)：37 －40.

[5]杨志荣，周建中.一种基于D-S证据理论的水轮机故障诊断方法[J].水电能源科学，2009，27(2)：152 －154.

[6]杨伟，顾明星，彭静萍.证据理论在电机故障诊断中的应用[J].电力系统保护与控制，2010，38(2)：64 －67.

[7]凌六一，黄友锐，魏圆圆.基于多传感器信息融合和神经网络的汽轮机故障诊断研究[J].中国电力，2010，43(3)：46 －49.

[8]石为人.基于灰色神经网络建模的水质参数预测[J].计算机应用，2009，29(6)：1529 －1535.

[9]贺建军，赵蕊.基于信息融合技术的大型水轮发电机故障诊断[J].中南大学学报：自然科学版，2007，38(2)：333 －337.

[10]谷敬佩，梁平.基于小波包分析和信息融合技术的汽轮机转子故障诊断[J].汽轮机技术，2010，52(4)：300－302.