谈灯具总光通量
文/[美]迈克·伍德 编译/姚涵春
(1.上海戏剧学院,上海 200040)
现在,灯具行业有各种各样的灯具光度测量值,特别是LED灯具产品说明书上所公布的那些技术数据。当试图评判一个灯具是否真的高效、节能时,可以寄希望于PLASA的标准草案E1-41,它对于测量和报告采用固态光源的娱乐灯具的光度特性数据会有帮助,但是,不是所有的灯具制造商都采用这个标准。
如果一个灯具声称是绿色、高效的,那就需要用合适的方法去核实它是否如此。遗憾的是,笔者可以保证,在当今的市场上,许多所谓的绿色产品实际上绝不是那么回事。
忘却华丽的辞藻,真理在数字之中。但是,如果一个制造商不给出完整的数据,该怎么办呢?如果读者至少拥有关于灯具光束的中心照度和受照区域的直径等相关数据,还是可以做一些事情的。
首先,来温习一下总光通量。图1阐明3种可能的光束剖面的轮廓:A是假设的完全平直型光束分布,B是常常呈现于椭球聚光灯的峰值型光束分布,而C则是拥有中央小凹和直的侧边的光束分布,这种光分布是很稀罕的,但是,有时呈现于菲涅尔透镜聚光灯具中。3种光束形状都确切地拥有相同的中心照度数据,如图中红色虚线所示。这意味着,测光仪分别放置于光束中心a、b、c 三点上,它们的读数是相同的。

图1 三种可能的光束轮廓
那么,中心照度(以烛光(footcandle)或勒克斯(lux)为计量单位)并没有说明来自灯具的总光通量有多少流明。要做到这一点,必须在整个光束上都有相对应的照度读数。如果将光束图形类比成储水桶。图1中的第二排光束轮廓与第一排相同但是完全颠倒的,构成U形。最后一排则是将U形图线旋转而构造成的储水桶。平直型光束A构造成一只圆柱形水桶,而其他两个光束B和C则构造成形状更复杂的水桶。
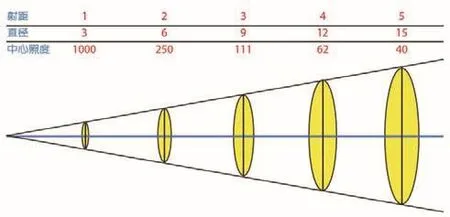
图2 中心照度、光斑直径和射距的V形图表
如果将这些想象中的水桶装满水,那么,每个水桶所拥有的水量可以类比为灯具光输出的总流明数。(例如,水桶A比水桶B拥有更多的水。)流明数是总光通量的测量数值,而不是光强度的测量数值,所以,一个宽大而浅的水桶拥有的水量可能与一个窄小而深的水桶的水量一样多。同样地,一只具有宽大而峰值较小的光分布的灯具实际上与狭窄而峰值较大的光分布的灯具拥有一样多的光输出。这是因为那些流明的光被分摊于更宽广的面积上。
如果掌握的全部资料只是中心照度和光斑直径的数据图表,那该如何估算灯具的总光通量呢?图2这类V形图表式的性能资料是非常常见的。(注意:这种技术只适用于拥有圆形、对称光束的灯具,而不适用于非对称光束的灯具,如天幕灯具。)
这个表格和图形展示了在一系列射距上的光斑直径和中心照度。笔者特意在此图表中隐去了各个物理量的单位。只要这些物理量的单位相互关联一致,不论采用米(m)和勒克斯为单位,还是采用英尺和烛光为单位,都适用于笔者随后的阐述。即,如果射距和直径以米作单位,那么照度的单位应该用勒克斯,同样的,如果射距和直径的单位是英尺,那么,照度的单位应该采用烛光。
虽然对灯具光束的轮廓事先一无所知(峰值分布还是平直分布),但还是能作出某些假设,从而能得到灯具光输出有多少流明的方法。首先,假设不具有如同图1C——中央有一小凹的光分布。那是常规灯具不常见的特殊光分布,所以,将它排除在外是合理的。至此可知,光分布或是如图1A的完全平直型的光分布,或更可能是某种峰值型的光分布,其中心照度最高,而后光照度向光斑边缘逐渐下降,如图1B所示。
因此,在这两种光分布中,完全平直型光束具有最多的流明,如果能估算出它的总光通量,那么,就掌握了这种灯具产生的总光通量的最大流明数。
图3更详细地显示出这种情形。
需要知道旋转体的体积(储水桶里的水量)以得到灯具的总光通量。像这类圆柱体的光分布,其数学运算是简单的:圆的面积等于π乘以直径的平方再除以4,即A=π×D2/4。总光通量等于中心照度(C)乘以这个面积(A)或C×A。
如果用图2表格中的某数值代入,就能将总光通量计算出来。采用表中射距为1的相应数值,查找到直径为3,中心照度为1 000。
因而,其总光通量=π×32×1000/4=7 068 lm。
(如果采用的单位分别是米和勒克斯或英尺和烛光,这没有什么问题。只要不混用相关联的单位,其用流明为单位的答案应该是相同的!)
如果尝试另一个射距,或许其数据为5英尺时,其光通量又如何呢?将射距5所对应的直径为15和中心照度为40的数值代入公式,得到:
总光通量=π×152×40/4=7068 lm。
可见,总光通量并不受射距的变化而变化。如果原始的V型图表数据是准确无误的,它将给出相同的答案,或者说在任何射距上光斑的总光通量是非常接近的。
由上文可知,这台灯具总光通量的最大流明数:7 068 lm。事实上,灯具发射出的光束不会是完全平直型的光分布,所以,这个数字将被缩减,但是,被缩减多少呢?图4表示了一种可能的情况。
虽然仍可以得到C和D的数据,但是这个斜边水桶的总体积将小于圆柱体水桶的总体积。
如果假设其光分布确实是一条余弦曲线,则能够计算出理论上减少的光输出。例如,某成像灯边缘亮度是中心亮度的1/3,(即中心的亮度和边缘的亮度之比为3:1),它发出的余弦曲线光分布将拥有平直型光分布光输出总流明的65%(见表1)。表1表示中心和边缘的各种亮度比的一系列相关数据。

图3 计算旋转体的体积
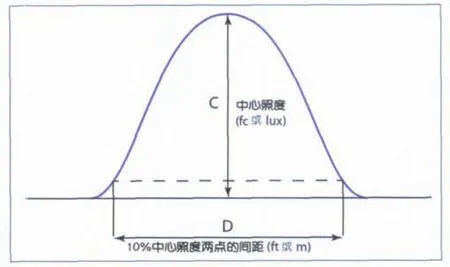
图4 估计中心与边缘的亮度比
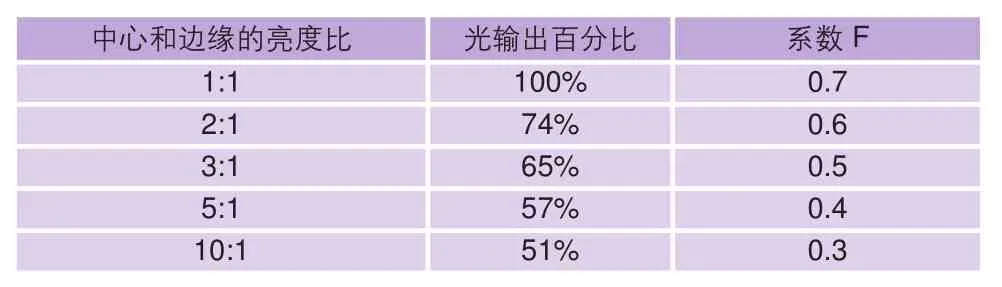
表1
进一步论述,对于更加复杂多变的实际情况,大多数灯具的光分布并不是真实的余弦曲线。尤其是柔光灯(Wash lights),它的光分布呈现出更为接近峰值型的光分布,比较平直型光分布将减少更多的光输出,或许会再进一步减少20%。
然而,这些都是推测的。现在能够对总光通量作出估算。虽然可能不知道中心和边缘的亮度比,但有一个好的经验法则是,对于柔光灯采用10:1,而对于聚光灯则采用3:1。其亮度比取决于光束分布是如何平直。有些比这个相应数值更高些,但有些则可能更低些。在实例中,可以假设样灯是一台聚光灯,运用65%的缩减比例,从而得到最终的结果是:7 068×65%=4 500 lm.
这个方法可能看上去仍然有点复杂,如果只为寻求粗略的答案,可以简化这个数学算式,以估算出灯具的总光通量,因而在表1最后一列中明示出各亮度比状态下的总系数F。这就给出了如下的经验公式:
总光通量 = F×(光斑直径)2×中心照度
表1中的F数值是依据对中心和边缘的亮度比的评估。如果不知道亮度比,那么就采用:F=0.4作为平均数值,当然它不够精确。因为如果灯具实际上拥有一种不同寻常的光分布,这种算法可能往往是不符合实情的。灯具制造商可能不赞同这种估算方法,如果制造商能够给予完整而有效的信息,便不需要这样估算。如果不具有完整的数据,这个近似方法将至少给出大致正确的答案。而且它也很简单,可以迅速地估算出来。
一经掌握总光通量的评估,使用者就能达到真正的目标:试着评估某款灯具是否高效、节能,并运用这种方法计算出灯具的光效。如果如图2所示的实例灯具的功耗为300 W,那现在就能估算,它具有的光效为:4 500/300=15 lm/W。这个结果不是精确的结果,也决不是替代包括总光通量正确测量值在内的完整数据。然而,如果没有别的信息,做这个简单的数字运算可能得到一种感觉:总光通量是如何受到光束轮廓的影响,而灯具实际上又是如何节能的。

