移动通信铁塔直击雷电流分布的研究

李 鹏 吕英华 李子伟 丘四海 杨文翰 刘 宁 刘吉克

（1.北京邮电大学电子工程学院，北京 100876；2.中讯邮电咨询设计院，河南 郑州 450007）

引 言

建筑物、交通工具、电子设备及元器件都有可能因雷击而受到影响甚至遭到破坏。已有学者对不同物体进行防雷与接地技术研究［1-4］。近年来，雷电与高耸物体的相互作用也已得到雷电研究者们相当的关注［5］。移动通信基站铁塔遭雷电直击时，塔体上产生的雷电流分布必然对移动通信基站系统形成干扰。

作为自然界中的随机现象，雷电参数必须通过地面数据测量给予概率形式表达［6］；雷击间距的计算方法尚不统一［7］；如何优化设计接地网以得到更好的高频和动态性能仍无定论［8］。这些现状使得研究移动通信基站铁塔直击雷电流分布的问题十分复杂，目前还没有针对这一问题的具体研究成果。

云地放电形成的先导从云中电荷中心伸向地下所感应的电荷，这就引起从云到地的向下放电，或从接地（物）体向云体发展的向上先导［9］。放电电荷经雷云到地面物体，再由地面物体入地到雷云覆盖的大地，最终在雷云覆盖的大地与其正上方的雷云中和。这一过程（如图1示）使雷云-铁塔-接地网-雷云覆盖的大地构成一个回路。基于此，可建立基站铁塔及其接地网的电路模型用于研究基站铁塔冲击阻抗特性及直击雷电流分布。该方法可分析雷电直击铁塔对周边设备造成的干扰。

图1 回路框图

1.理论建模

1.1 雷电流模型

雷电是一种复杂的现象，雷电流波形具有随机性。大量观测表明，雷电流波形的主要特点是:波头急速上升且持续时间极短，其形状近似余弦曲线的上升段；波尾缓慢下降，持续时间远远大于波头的持续时间；雷电流的峰值通常会达到数百千安。

目前，常用的雷电流模型解析表达函数主要有双指数型函数和Heidler函数。1941年，Brucet和Golde提出双指数型函数雷电流模型

1995年国际电工委员会在IEC61312-1标准中建议用Heidler函数作为雷电流模型

但是，雷电流波头的急速上升是移动通信基站系统受到冲击危害的最主要根源。因此，在防雷设计中只需要考虑雷电流波头就足以估算直击雷电流对移动通信基站系统造成的干扰。单周期余弦脉冲函数满足上述条件，可作为雷电流模型

式中雷电流的假设参数如表1所示所示。

表1 单周期余弦脉冲雷电流模型参数

在该角频率上，对应的波长约为2386m.大部分铁塔的高度小于波长的1／20，所以可用电路方法将铁塔上的每个部件用相应的电器件表示，然后按集总电路模型处理。该模型中电流源的输入电流满足式（3）。

1.2 器件参数

1.2.1 铁塔钢材电阻的近似计算

对于单周期余弦脉冲型雷电流模型，能量相对集中在角频率ω=0.79M （rads／sec）上，可以用该角频率的表面电阻表示钢材电阻特性。移动通信基站铁塔上的钢材主要有管钢、扁钢和角钢。计算其相应的趋肤深度δ（如图2所示）即可得表面电阻。

1.2.2 铁塔钢材电感的近似计算

已有相关标准［10］建议钢材电感参数的近似计算方法。式（4）和（5）分别适用于带状体钢材电感和棒状体钢材电感。

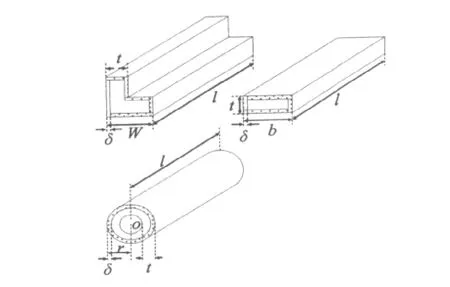
图2 不同形状钢材的趋肤深度

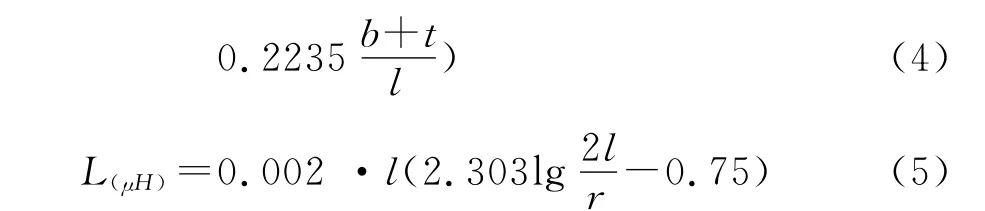
式中:长度l、宽度b、半径r及钢材厚度t均以厘米计量。

经计算，趋肤深度δ约为31.7μm，远远小于钢材厚度t，说明:雷电流只在管钢外表面上很浅的外层流过，管钢电感的计算方法可按棒状体处理。关于角钢电感的计算，可用一个等效的带状体钢材替代角钢，即将角钢的横截面展开成矩形（b=2 w），该等效带状体钢材的电感即为角钢的近似电感。

1.2.3 铁塔钢材间电容的近似计算

基本平板电容器的相对面积和距离决定了其电容参数。类似地，两块钢材间的电容可根据它们的相对侧面积和距离来近似计算。每根钢材可用一根假想的铁棒等效表示。令该铁棒与实际钢材等长且侧面积相等，即横截面周长相等，则铁棒的等效半径r=钢材横截面周长／2π.两根钢材间的电容参数就转换为空间两导线（假想铁棒）间的电容参数。可按空间投影方法计算两导线间的距离和相对长度。

如图3所示，两实线a和b分别表示空间中两导线（假想铁棒）。将a以其自身中点M 为支点，向b方向旋转构成投影虚线a′.a′与b的距离d即为二者的空间距离；投影虚线a′与b可以重叠的长度l即为二者的相对长度。根据文献［11］提供的方法，由半径、空间距离和相对长度可确定电容参数:

图3 空间投影方法

式中:r1和r2分别为两导线的等效半径；且有

值得注意的是，彼此空间垂直的两根钢材之间相对侧面积极小，可忽略其间的电容。

经计算，钢材电阻多为亚欧姆量级（×0.1Ω），钢材电感多为亚微亨量级（×0.1μH），钢材间电容值最高在十倍皮法量级（＜10pF）.对于能量集中在ω=0.79M （rads／sec）的雷电流，钢材阻抗Z多为亚欧姆到欧姆量级（×0.1Ω～Ω），钢材间容抗Zc均高于亚兆欧姆量级（＞0.1MΩ）.所以钢材间电容上的电流约为钢材上流过电流的10-5甚至更小。说明:在分析移动通信基站铁塔上的直击雷电流分布时，钢材间电容可忽略不计。

1.2.4 接地体电气参数的近似计算

接地网中的接地体特性由两部分因素决定:金属特性和接地特性。金属特性表现出的电阻RM和电感LM的计算方法与上述钢材电阻和电感相同；接地特性表现出的接地电阻和接地电感（RG和LG）需另外计算。文献［12-14］对不同接地体的RG和LG的计算已给出了参考。

接地电阻和接地电感反应了电流流过接地体时向无限远处泄漏电流的性质。这里，“无限远”只是相对接地体尺寸而言。通常，接地体的尺寸只有数米，而雷云覆盖的范围则可达数十甚至数百千米。所以，雷云覆盖的大地也应理解为“无限远”。从接地体上泄露出的电流最终流向雷云覆盖的大地（无限远），电荷在此处与其正上方的雷云中和。

若某根接地体的一端与其他钢材或接地体相连，而另一端与大地相连，则可以将电阻RM、电感LM、接地电阻RG和接地电感LG四者串联表示此接地体的全部特性。而对于两端都与其他钢材或其他接地体相连的接地体，可将其作拆分处理:假设电流iin由接地体的一端流入，而由另一端流出iout.期间，电流每流过一小段接地体就向无限远处泄漏少量电流，最终总共向无限远处泄漏电流ileak.则有iin=iout+ileak.根据此式，可将该接地体拆分为两段，每段的电阻和电感均取半值（1／2 RM和1／2 LM），再由分段处加一支路。该支路上的电器件为接地电阻RG与接地电感LG的串联，并且该支路的一端连接接地体分段处，另一端连接雷云覆盖的大地（无限远）。

1.2.5 天线电缆屏蔽层电气参数的近似计算

天线电缆屏蔽层电阻的计算与上述钢材电阻的计算方法类似，只需用屏蔽层的趋肤深度替换钢材趋肤深度即可。而天线电缆屏蔽层电感的计算需要分析实际建筑结构。如图4所示，电缆与塔身相连，然后平行拉线至机房顶部。平行的电缆屏蔽层与地面构成一个“单线—大地”回路。那么天线电缆屏蔽层每单位长度的外电感可由式（7）计算［15］。

式中:h表示电缆对地面高度；r表示电缆半径。对于屋顶自立塔，电缆仍由顶部进入机房，其对地高度也是h.进入机房后，电缆一般沿机房顶部走线，然后进入设备。所以，绝大部分长度的电缆屏蔽层对地高度仍然是h，仍可用式（7）近似计算天线电缆屏蔽层的外电感。

图4 铁塔与机房的实际建筑结构

1.3 雷击点

雷击点对应电路模型中电流源的位置，不同的雷击点表示电流源从不同的节点注入电流。

目前，滚球法（Rolling Sphere Method）被广泛应用于建筑物防雷领域。该方法可表述为空间中有一半径为雷击间距（rs，滚球半径）的假想球体，该球体沿建筑物表面滚动，所有与该球体相接触的建筑物表面都有可能成为雷击点。

雷击间距（rs）的理论计算方法还没有统一的定论。但是，各国或相关组织制定的防雷设计标准对建筑物进行防雷级别划分，针对各防雷级别的建筑物给出了雷击间距的参考值。我国的建筑物防雷设计标准将建筑物分为三个防雷级别，其滚球半径rs分别参考30m、45m和60m.国际相关标准将建筑物分为四个防雷级别，其滚球半径rs分别参考20m、30m、45m 和60m［16］.基于此，只需要考虑20m以上范围的雷击点。另外，根据文献［17］的研究，当建筑高度大于60m时，雷击点将不易确定。

笔者选用限制性扩散凝聚生长模型［18］进行雷击铁塔概率的研究，因篇幅所限，将另据文章发表。初步研究表明，对于略高于60m的铁塔，雷击概率较大的雷击点应出现在20m、25.5m、30m、34.5 m、39.3m、45.3m、50m、55m 和塔尖处。故可选取上述诸点作为雷击点。

通过以上一系列近似计算，可建立起一个完整的“铁塔—接地网”网络的电路模型，并选择雷云覆盖的大地作为电路模型的参考点。

2.仿真结果分析

以雷击铁塔塔尖为例，图5给出了在铁塔不同高度上某根主梁的雷电流分布（ρ=100Ω·m）.

由图5（a）可以看出，雷击塔尖时，主梁上的所有钢材的雷电流分布在同一时刻（4.002μs）出现峰值。此时，塔尖的避雷针承载了全部雷电流，其峰值等于雷电流峰值（400kA）.

图5 主梁雷电流分布（雷击塔尖，ρ＝100Ω·m）

铁塔末端由四根相同的塔脚连接大地。铁塔上的雷电流必须汇集到这四根塔脚上，然后流入接地网。所以塔脚上的雷电流分布峰值约为雷电流峰值的1／4（即100kA）.

将其他高度上该主梁的雷电流分布情况放大至图5（b）进行观测。通常，塔身较高处架设有天线及天线平台，天线平台由各种不同形状的钢材或钢板纵横交错连接构成且结构复杂，所以这一高度上的主梁的雷电流分布较小。如图5（b）所示，4／5倍塔身高度上的主梁的雷电流分布峰值为32.282kA.

3／5倍塔身高度和2／5倍塔身高度上主梁的雷电流分布较大，峰值分别为36.339kA和36.763kA.这一段属于塔身的中间部分，其结构简单且彼此相似，所以这一段高度上的主梁的雷电流分布较大且彼此相似。

塔身底部担负承重作用，斜梁数目多且结构极其复杂，所以这一高度上的主梁的雷电流分布最小。如图5（b）所示，1／5倍塔身高度上的主梁的雷电流分布峰值仅为27.498kA.

说明:铁塔主梁上的雷电流分布情况依赖铁塔的实际建筑结构。结构越复杂，主梁上的雷电流分布越小，反之亦然。

图6给出了雷击塔尖时（ρ=100 Ω·m），在铁塔不同高度上的斜梁的雷电流分布。塔尖架设一根避雷针并无其他斜梁，所以只考察其他高度上的斜梁的雷电流分布情况。

由图6可见，所有斜梁的雷电流分布峰值也均出现在4.002μs.斜梁的雷电流分布情况也与铁塔的建筑结构有关。铁塔的建筑结构决定了铁塔上的雷电流必须通过铁塔上的钢材向塔脚汇集，然后通过塔脚连接接地网。所以在塔身较低高度上的斜梁的雷电流分布峰值较大，而塔脚附近的斜梁的雷电流分布峰值最大。如图6示，1／5倍塔身高度上的斜梁的雷电流分布峰值约为22.5kA，塔脚附近的斜梁的雷电流分布峰值约为30.905kA.

在塔身较高处的主梁上的雷电流分布峰值较小。相应地，在这一高度上的斜梁的雷电流分布峰值就较大。如图6示，4／5倍塔身高度上的斜梁的雷电流分布峰值为19.983kA.

其他高度属于塔身的中间部分，其主梁的雷电流分布较大且彼此相似，所以在这一高度上的斜梁的雷电流分布峰值较小且彼此相似。如图6所示，2／5倍塔身高度3／5倍塔身高度上的斜梁的雷电流分布峰值分别为14.137kA和14.771kA.

由上述数据分析可知，铁塔上的雷电流分布情况与铁塔结构有关。

另外，当雷击发生在其他位置时，铁塔上的雷电流分布情况较雷击塔尖的情况有明显的区别。雷击发生在不同的位置，相当于在“铁塔-接地网”网络中的不同节点上注入电流，所以在该网络中必然形成明显不同的电流分布。说明:铁塔上的雷电流分布情况与雷击位置有关。

仍以雷击塔尖为例，表2和表3分别列出了大地电阻率ρ=5000Ω·m时铁塔主梁与斜梁上的雷电流分布情况。与上述大地电阻率ρ=100Ω·m时的情况相比，雷电流分布峰值出现的时刻相差不到0.6%，且各峰值大小与上述大地电阻率ρ=100 Ω·m时的情况也极其相近。

表2 主梁雷电流分布（雷击塔尖，ρ＝5000Ω·m）

表3 斜梁雷电流分布（雷击塔尖，ρ＝5000Ω·m）

而且，当雷击发生在某一其他位置时，在不同大地电阻率条件下，铁塔上雷电流分布情况也十分相似。说明，铁塔上的雷电流分布情况几乎不受大地电阻率的影响。

计算结果显示，天线电缆屏蔽层的电阻与铁塔钢材电阻或接地体的金属特性电阻处于同一量级，而其电感大约比铁塔钢材电感或接地体的金属特性电感高两个数量级。天线电缆屏蔽层的一端连接铁塔，另一端通过基站设备外壳与接地网相连。天线电缆屏蔽层是“铁塔—接地网”网络的一条并联支路。那么，铁塔的结构必然影响天线电缆屏蔽层上的雷电流分布。

仿真结果表明，在同一大地电阻率条件下（ρ=100Ω·m），天线电缆屏蔽层上的雷电流分布峰值随雷击位置的高度而变化。雷击发生在塔尖时，天线电缆屏蔽层上的雷电流分布峰值约为27.01kA.当雷击位置的高度逐渐降低时，天线电缆屏蔽层上的雷电流分布峰值也逐渐降低。雷击发生在20m高度时，天线电缆屏蔽层上的雷电流分布峰值下降到最小值，约为26.8kA，较雷击塔尖时下降了0.78%。说明，天线电缆屏蔽层上的雷电流分布仅随雷击高度正向变化，但变化量不显著。

表4列出了雷击塔尖时，不同大地电阻率条件下的天线电缆屏蔽层上的雷电流分布的仿真数据。由表4可见，两峰值相差不到0.112%，且两峰值出现的时间差约为0.013μs，仅为周期时间的0.17%。

表4 雷击塔尖时天线电缆屏蔽层上的雷电流分布

当雷击发生在其他位置时，两峰值相差均在0.1%～0.11%的范围之内，且峰值出现时刻的差均不超过0.022μs，小于周期时间的0.28%。说明天线电缆屏蔽层上的雷电流分布情况几乎不受大地电阻率的影响。

在接地网的四条边上等间距地埋设有垂直接地体，并且在接地网的四个角上埋设有伸向四周的水平接地体。铁塔上的雷电流将通过这些接地体产生入地电流。图7列举了在大地电阻率ρ=5000 Ω·m且雷击塔尖的情况下，在接地网四角上的水平接地体上的入地电流波形。如图7所示，四个峰值相差范围只在0.0035%以内，且峰值出现时刻均为3.997μs.

图7 接地网四角上的水平接地体入地电流（雷击塔尖，ρ＝5000Ω·m）

当ρ=100Ω·m且雷击发生在其他位置时，接地网中的垂直接地体上的入地电流也非常相似。

说明任意位置的直击雷在接地网对称位置的接地体上产生几乎相同的入地电流，而不会随雷击位置而产生明显变化。

雷击塔尖时，雷电流首先要全部流过避雷针，然后再流到铁塔钢材上。而雷击其他位置则表示雷电直接击中铁塔塔身，在对应的模型中，此时的避雷针相当于被“悬空”处理，其上没有电流。因此，在讨论“铁塔—接地网”网络的整体冲击阻抗特性时，雷击塔尖的情况应作为一种特例，不能与其他情况直接进行比较。

表5列举了ρ=100Ω·m时不同雷击高度条件下“铁塔—接地网”网络的整体阻抗特性。可以看出:整体电阻和电抗随雷击点距地面高度的增加会有略微增大，其中电抗的变化比电阻的略大。类似地，ρ=5000Ω·m条件下的整体阻抗特性也基本呈现上述特性。

表5 “铁塔—接地网”网络整体阻抗（ρ＝100Ω·m）

3.结 论

移动通信基站铁塔在遭遇直击雷时必然对周边设备和仪器产生干扰，以下相关结论为分析这些影响提供了重要参考:

1）铁塔上的雷电流分布与铁塔结构有关，并且随雷击位置的不同表现出明显的区别，但几乎不受大地电阻率的影响；

2）天线电缆屏蔽层上的雷电流分布与铁塔结构有关，并且随雷击高度产生微小的正向变化，但几乎不受大地电阻率的影响；

3）任意位置的直击雷在接地网对称位置的接地体上产生几乎相同的入地电流，而不会随雷击位置产生明显变化；

4）“铁塔—接地网”网络的整体电阻和电抗随雷击点距地面高度的增加会有略微增大，其中电抗的变化比电阻的略大。

［1］NUCCI C A，RACHIDI F，IANOZ M，et al.Lightning-induced voltages on overhead lines ［J］.IEEE Transactions on Electromagnetic Compatability，1993，35（1）:75-85.

［2］TESCHE F M.Comparison of the transmission line and scattering models for computing the HEMP response of overhead cables［J］.IEEE Transactions on Electromagnetic Compatability，1992，34（2）:93-99.

［3］ISHII M，MICHISHITA K，HONGO Y，et al.Lightning-induced voltage on an overhead wire dependent on ground conductivity［J］.IEEE Transactions on Power Delivery，1994，9（1）:109-115.

［4］PLUMER J A，ROBB J D.The direct effects of lightning on aircraft［J］.IEEE Transactions on Electromagnetic Compatability，1982，24（2）:158-172.

［5］RACHIDI F.Modeling lightning return stroke to tall structures:a review［J］.Journal of Lightning Research，2007，1:16-31.

［6］CHOWDHURI P，ANDERSON J G，HISHOLM W A，et al.Parameters of lightning strokes:a review［J］.IEEE Transactions on Power Delivery，2005，20（1）:346-358.

［7］NASSEREDDINE M，HELLANY A.Designing a lightning protection system using the rolling sphere method［C］／／Second International Conference on Computer and Electrical Engineering （ICCEE'09）.Dubai，UAE，2009，1:502-506.

［8］GRCEV L.Impulse efficiency of ground electrodes［J］.IEEE Transactions on Power Delivery，2009，24（1）:441-451.

［9］戈尔德.雷电（上卷）［M］.周诗健，孙景群，译.北京:电力工业出版社，1982:73-77.

［10］National Fire Protection Association.ANSI／NFPA-70-1993［S］.National Electrical Code（NEC），1993.

［11］焦其祥.电磁场与电磁波［M］.北京:科学出版社，2007:157-158.

［12］SUNDE E D.Earth Conduction Effects in Transmission Systems［M］.U.S.A.:The Bell Telephone Laboratories Series，1949:69-89.

［13］高攸纲.屏蔽与接地［M］.北京:北京邮电大学出版社，2004:132-148.

［14］李景禄，胡毅，刘春生.实用电力接地技术［M］.北京:中国电力出版社，2001:13-36.

［15］PAUL C R.Introduction to Electromagnetic Compatibility［M］.2nd ed.New York:John Wiley ＆Sons，2006:184-196.

［16］IEC.TC 81IEC 62305-3Protection against lightning-Part 3:Physical damage to structures and life hazard［S］.American National Standards Institute（ANSI），2006.

［17］AIT-AMAR S，BERGER G.A modified version of the rolling sphere method［J］.IEEE Transactions on Dielectrics and Electrical Insulation，2009，16（3）:718-725.

［18］吕英华.计算电磁学的数值方法［M］.北京:清华大学出版社，2006:96-99.