粘弹性介质地震波传播特征及反射特征研究

王小杰，印兴耀，吴国忱

（中国石油大学，山东青岛 266555）

粘弹性介质地震波传播特征及反射特征研究

王小杰，印兴耀，吴国忱

（中国石油大学，山东青岛 266555）

理想弹性介质并不能解决许多复杂的实际问题。在实际介质中，地震波的传播过程存在吸收作用，使地震波能量发生了损耗、频带变窄、相位延迟、频率降低，尤其是高频部份。这种特性可以用传播矢量和衰减矢量来表示，衰减矢量越大，介质的吸收越强。这里通过引入广义平面波、纵横波品质因子以及衰减角，利用应力应变关系和连续性条件，推导了粘弹性介质精确的Zoeppritz方程，并通过求解精确的Zoeppritz方程，分析了粘弹性介质中传播矢量、衰减矢量、纵波反射系数、转换波反射系数与频率、衰减角、入射角、品质因子、速度等物理量之间的关系，详细地了解了粘弹性介质中地震波传播特征及反射特征，为粘弹性介质中储层预测问题的研究提供了理论基础。

粘弹性介质；传播矢量；衰减矢量；反射系数；衰减角

0 前言

在地震勘探中，把远离震源处绝大部份地带的岩石都可近似看作理想弹性体。这样弹性力学中的许多理论都可以直接应用到地震勘探中来，从而将问题进行简化。但是随着油气勘探、开发工作的不断发展，地震勘探的重点由原来的构造油气藏向岩性油气藏、隐蔽油气藏转移，应用理想弹性介质并不能解释许多复杂的实际问题。学者们通过对大量观测结果的分析，发现地震波在岩层中传播时有吸收作用，即吸收激发脉冲的某些频率成份，尤其是高频部份，使能量也发生了损耗。因此，实际岩石既有弹性，也会表现出像粘性流体那样的粘滞性［1］。

平面波在粘弹性界面的传播特征，很多学者做了大量的研究。郭智奇等［2］研究了层状粘弹性介质中SH波的反射、透射问题，从本构方程的角度，以波尔兹曼叠加原理为基础，建立积分型本构方程，进而建立粘弹性介质波动方程。孙成禹［3］等研究了平面波在粘滞性界面的反射特征，证明了粘滞性界面上的反射系数与入射波频率有关的特征。尹陈等［4］基于常规波动方程正演理论，添加了弥散～粘滞性特征，从岩石的内摩擦和粘滞系数上模拟粘滞性介质中地震波的衰减理论。

作者在本文通过引入广义平面波，运用应力应变关系和连续性条件，推导了P波入射到粘弹性界面的精确的Zoeppritz方程，通过求解精确的Zoeppritz方程，研究粘弹性介质中传播矢量、衰减矢量、反射系数与频率、衰减角、入射角、品质因子速度等物理参数之间的关系，为以后公式的简化以及粘弹性介质中油气预测提供了理论基础。

1 粘弹性介质精确的Zoeppritz方程

早在上世纪初已基本建立了平面波在弹性界面中的反射理论，这也是一直以来地震勘探的理论基础。但是实际介质并非理想的弹性介质，具有一定的粘滞性。当一平面P波传播到粘弹性界面R时，会产生反射P波、反射SV波、透射P波、透射SV波，如下页图1所示。选择直角坐标系，使y轴与波前面平行，在这种情况下，波函数与y轴无关z＝0平面与介质分界面重合，z轴垂直向下，指向介质“2”，入射波来自z＜0的介质“1”，其中VP1VS1、ρ1、θp1、θs1、Qp1、Qs1分别表示介质“1”中的纵波速度、横波速度、密度、纵波入射角、横波反射角，纵波品质因子和横波品质因子；VP2、VS2、ρ2、θp2、θs2、Qp2、Qs2分别表示介质“2”中的纵波速度、横波速度、密度、纵波透射角、横波透射角，纵波品质因子和横波品质因子。假设广义平面波从介质“1”入射到界面，则可以分别写出入射P波、反射P波、反射SV波、透射P波和透射SV波的位移位函数。

图1 入射P波和反射波、透射波的关系Fig.1 The relationship between the incident P wave and the reflected wave、the transmitted wave

（1）介质“1”中的位移位函数：

入射P波：

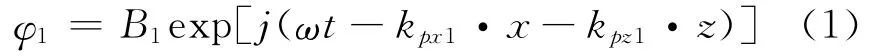
反射P波：

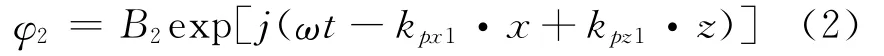
反射SV波：

（2）介质“2”中的位移位函数：

透射P波：

透射SV波：

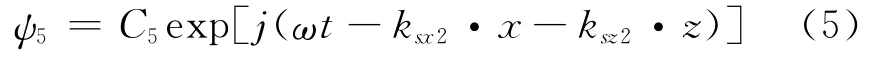
其中 kpx1、ksx1、kpx2和ksx2分别是五个波沿X方向的波数，即水平波数；kpz1、ksz1、kpz2、ksz2分别是五个波沿Z方向的波数，即垂直波数；B1、B2、C3、B4、C5分别是五个波的振幅。它们都是复数，这是与完全弹性介质的不同之处。由广义Snell定律知，五个波的水平波数都相等，入射P波和反射P波的垂直波数都相等［5、6］。

根据Q值表达式，定义纵横波品质因子［7］：

其中 QP和QS分别是纵波和横波的品质因子；λ和μ为拉梅系数，是复数；下标“R”和“I”分别表示对应量的实部和虚部。

用相速度和品质因子表示复波数，用复波数定义，可推导出复横波数和复纵波数的表达式：

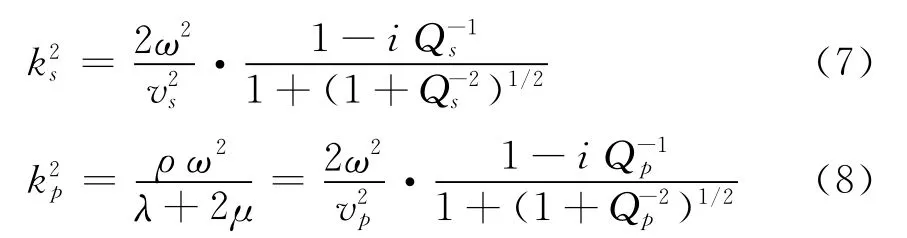
一般地，传播矢量和衰减矢量是不平行的，这时的波称为非均匀波。特殊地，当传播矢量的夹角为零时，波是均匀波。

由式（8）和式（10）得到

由式（11）的实部和虚部相等求解，可得：

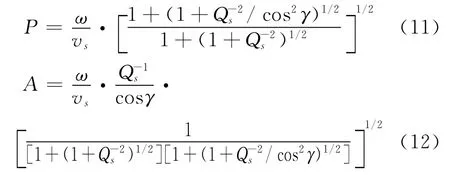
同理可得P波的传播矢量和衰减矢量。

由质点的位移分量与位移位的关系，可得到位移表达式（14）。

由应力应变关系和位移位关系得到应力表达式

分别把介质“1”和介质“2”中的位移位函数带入位移和应力表达式，其中下标“1”和“2”分别表示介质“1”和“2”中的量。在界面z＝0处，这五个波应满足位移连续和应力连续，进而可推导得到如下精确的Zoeppritz方程（16）：

2 粘弹性介质地震波传播及反射特征分析

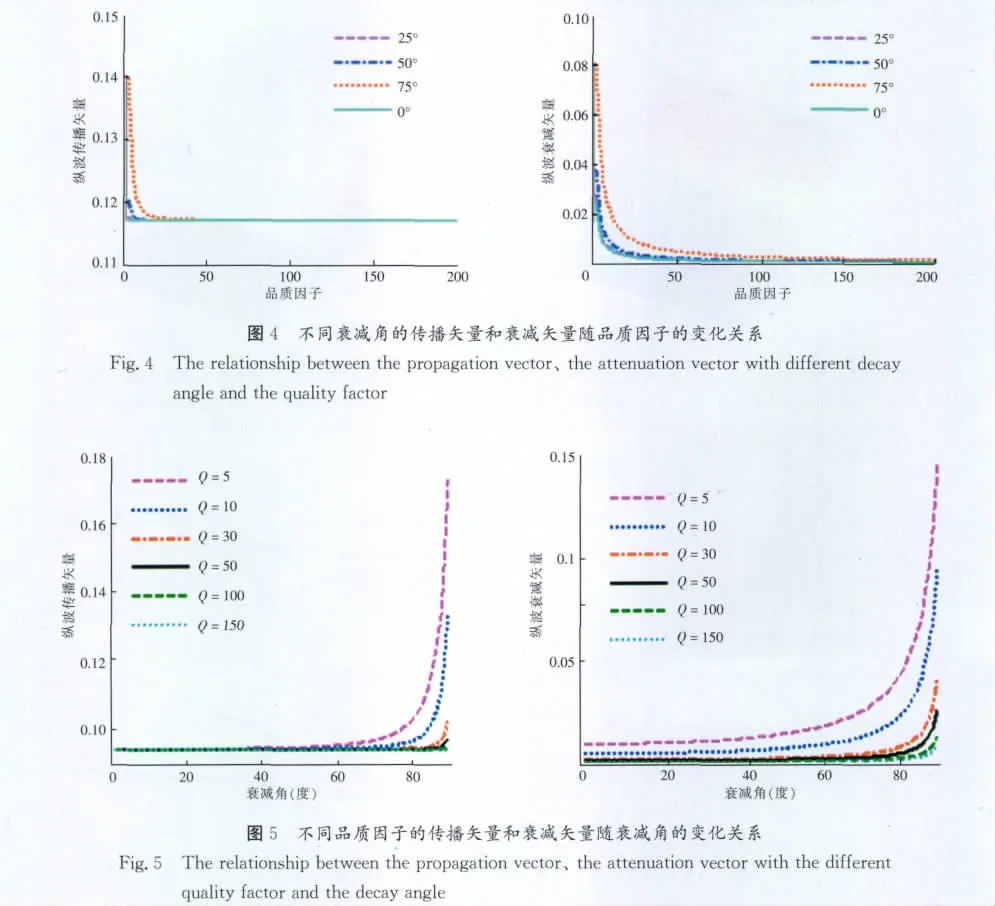
通过上面的粘弹性介质精确的Zoeppritz方程推导，可以看出粘弹性介质的复波数是通过传播矢量和衰减矢量来表示的，其中复波数的实部是传播矢量，虚部是衰减矢量。下面以纵波为例，分析纵波的传播矢量、衰减矢量分别与衰减角、品质因子、速度之间的关系。图2和图3分别是当频率为30Hz、速度为2 000m/s时，传播矢量和衰减矢量随衰减角和品质因子的变化关系图。从图2及图3中可以看出，只有当衰减角比较大时，衰减角对传播矢量和衰减矢量的影响较大，在接近90°时，达到最大，而当衰减角较小时，影响不大。品质因子对传播矢量的影响较小。

为了便于分析，我们从中抽取了几道进行比较，如下页图4所示，其中不同的曲线代表不同的衰减角。从图4中可以看出，衰减角越大，品质因子越小，对传播矢量和衰减矢量的影响越大。但是无论是衰减角还是品质因子，对衰减矢量的影响都大于对传播矢量的影响。图5（见下页）是在不同品质因子下传播矢量和衰减矢量随衰减角的变化关系。从图5中可以看出，当衰减角在0°到40°时衰减角对传播矢量和衰减矢量的影响几乎为零；当衰减角在40°到60°时，衰减角对传播矢量和衰减矢量的影响很小，尤其是传播矢量，几乎为零；当衰减角大于60°时，影响较大，并且随着衰减角的增大影响越大。通过以上结论可以看出，当衰减角在0°到60°时，对传播矢量和衰减矢量的影响都不大因此在下面的讨论中，假定衰减角为30°。

下页图6和图7是衰减角为30°，速度为2 000m/s时，传播矢量和衰减矢量随频率和品质因子的变化关系。下页图8是从中抽取的几道进行比较，其中不同的曲线代表不同的Q值。从图6～图8中可以看出，频率对传播矢量的影响是线性的，频率越高，传播矢量越大，品质因子对传播矢量的影响很小，几乎为零。而当品质因子一定时，衰减矢量随着频率的增大而线性增大，品质因子越小，衰减矢量增加得就越大。当品质因子大到一定值时，衰减矢量几乎为零，即频率和品质因子对衰减矢量的影响几乎为零。

后面图9和图10是当衰减角为30°，频率为30Hz时，传播矢量和衰减矢量随纵波速度和品质因子的变化关系。从图9及图10中可以看出，速度越小，传播矢量和衰减矢量就越大。并且随着速度的增大，传播矢量减少的很快，近似为线性，衰减矢量则衰减较慢。当品质因子较大时，衰减矢量接近于零，速度对衰减矢量的影响也接近于零。图11（见后面）是从中抽取的不同道进行比较，其中不同的线代表不同的品质因子。从图11中也可以看出，当衰减角、频率一定时，品质因子对传播矢量的影响几乎为零，对衰减矢量影响较大，品质因子越小，衰减矢量随着速度的增加，衰减的越快。

上面的分析是分别针对传播矢量和衰减矢量进行的。下面通过求解粘弹性介质精确的Zoeppritz方程，分析纵波和转换波反射系数的变化特征［8］。表1（见后面）是典型AVO模型的弹性参数表，参数分别表示纵波速度、横波速度、密度、纵波品质因子和横波品质因子。首先与弹性介质纵波反射系数特征进行比较，将表1的参数带入粘弹性介质精确的Zoeppritz方程，求解出不同衰减角的纵波反射系数模，如图12所示（见后面）。图12（a）是不同衰减角的纵波反射系数模与弹性介质纵波反射系数模随入射角的变化关系。从图12中可以看出，在小于临界角时，两者差异较小；在大于等于临界角时，差异较大，尤其是临界角附近，并且衰减角越大，差异越大。图12（b）是不同衰减角的纵波反射系数模与弹性介质纵波反射系数模的差值随入射角的变化关系，也可以看出在小于临界角时，差值在5%的范围内，衰减角越小，差异越小，在大于等于临界角时，差异较大，尤其是临近角附近。为了进一步了解粘弹性介质的反射特征，利用表1的数据，得到纵波反射系数随入射角和衰减角的变化关系［9］，如下页图13（a）所示。下页图13（b）是从中抽取的不同道进行比较，其中不同的线代表不同的衰减角。从图13中可以看出，当入射角小于等于临近角时，衰减角对纵波反射系数模的影响不大；当入射角大于临近角时，衰减角对纵波反射系数的影响较大，衰减角越大，影响越大。

下页图14（a）是转换波反射系数的模随入射角和衰减角的变换关系，下页图14（b）是从中抽取的几道数据，其中不同的曲线代表不同的衰减角从图14中同样可以看出，当衰减角比较大时，对转换波的反射系数影响较大；当衰减角比较小时，影响很小，尤其是在小角度入射时，影响更小。

表1 典型AVO模型的弹性参数Tab.1 The elastic parameters of typical AVO model

表2也是典型AVO模型的弹性参数表，参数分别表示纵波速度、横波速度、密度、纵波品质因子和横波品质因子，其中透射介质的纵波品质因子是变化的［10］。由上面的分析可知，当衰减角在0°～60°时，影响不大，因此假定衰减角为30°。下页图15（a）是不同品质因子的纵波反射系数模与弹性介质纵波反射系数模随入射角的变化关系，图15（b）是两者的差值随入射角的变化曲线。从图15中可以看出，在小于临界角时，两者差值非常小，几乎为零；在大于临近角时，差值较大，尤其是临近角附近，并且品质因子越小，差值越大。同时可以得到纵波反射系数模随入射角和品质因子的变化关系，如下页的图16（a）所示。图16（b）（见下页）是从中抽取的几道数据，其中不同的曲线代表不同的品质因子。从图16中可以看出，当衰减角一定且入射角在临近角附近时，品质因子对纵波反射系数模的影响较大。在大于或小于临近角时，影响都不是很大。

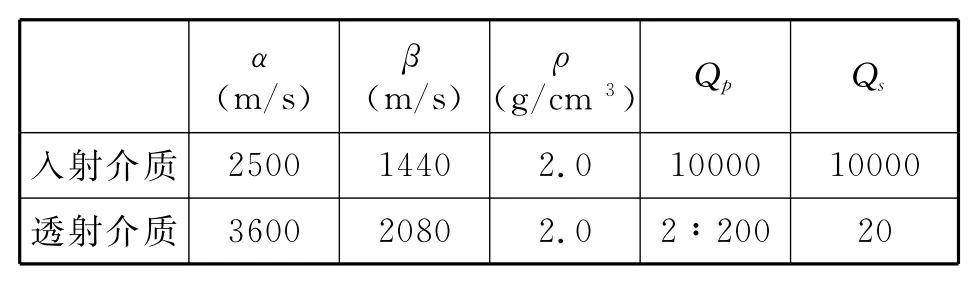
表2 典型AVO模型的弹性参数Tab.1 The elastic parameters of typical AVO model

图17（a）（见后面）是转换波反射系数模随入射角和品质因子的变化关系，图17（b）（见后面）是从中抽取的几道数据，不同的曲线代表不同的品质因子。从图17中可以看出，当衰减角一定时，在临近角附近，品质因子对转换波反射系数影响较大品质因子越小，影响越大。当入射角小于临近角时，品质因子越小，转换波波反射系数模越大，而当入射角大于临近角时，品质因子越小，转换波反射系数模越小。

3 结论与认识

粘弹性介质与弹性介质相比，更加接近于实际的地层介质，因此，随着地震勘探的发展，对粘弹性介质的研究是非常必要而有意义的［11～14］。作者在本文通过对粘弹性介质精确的Zoppritz方程求解与分析，得到了如下结论：

（1）衰减角对传播矢量的影响小于对衰减矢量的影响，当衰减角为0°到60°时影响较小。

（2）频率对传播矢量和衰减矢量的影响是线性的，并且当衰减角一定时，频率越大，传播矢量和衰减矢量也越大。

（3）速度对传播矢量和衰减矢量的影响也是接近于线性的，速度越大，传播矢量和衰减矢量越小

（4）当入射角小于临近角时，衰减角对纵波反射系数、转换波反射系数的影响较小；当入射角大于临近角时，衰减角对纵波反射系数、转换波反射系数的影响增大。

（5）当入射角在临近角附近时，品质因子对纵波反射系数、转换波反射系数的影响较大；在大于临近角和小于临近角时，影响不大。

在实际资料应用中，粘弹性介质Zoppritz方程除了需要纵横波速度与密度外，还需要品质因子参数，可以通过叠前地震资料S域谱比法，求取井位置处的品质因子曲线［11］，然后计算反射系数当然该方程在实际资料的应用中还需要做进一步的探讨，例如方程的简化等。

［1］ 孙成禹.地震波理论与方法［M］.山东东营：中国石油大学出版社.2007.

［2］ 郭智奇，刘财，张凤琴.层状粘弹性介质中SH波的反射、透射问题［J］.吉林大学学报，2005，35（增刊）：57.

［3］ 尹陈，贺振华，黄德济.基于二维粘滞性波动方程的地震波衰减理论研究［J］.物探化探计算技术，2008，30（5）：353.

［4］ 孙成禹，张玉亮，万学娟.平面波在粘滞性界面上的反射特征研究［J］.地球物理学进展，2007，22（2）：609.

［5］ 张玉华.基于岩石物理的AVO正演模拟研究［D］.东营：中国石油大学，2007.

［6］ 刘银斌，李幼铭，吴如山.横向各向同性多孔介质中的地震波传播［J］.地球物理学报，1994，37（4）：499.

［7］ 葛瑞.马沃可，塔潘.木克基.岩石物理手册：孔隙介质中地震分析工具［M］.合肥：中国科技大学出版社，2007.

［8］ 刘洋，李承楚，牟永光.双相横向各向同性介质分界面上弹性波反射与透射问题研究［J］.地球物理学报，2000，43（5）：691.

［9］ 殷八斤，曾灏，杨在岩.AVO技术的理论与实践［M］.北京：石油工业出版社，1995.

［10］SCHOENEGRG M.Elastic wave behavior across linear slip interfaces［J］.J.Acoust.Soc.Am，1980 68（5）：1516.

［11］孙成禹，杜世通.平面声波在粗糙界面上的反射特征研究［J］.地球物理学报，2006，49（3）：903.

［12］孙成禹.粗糙界面地震反射波场的滤波特性［J］.石油地球物理勘探，2004，39（1）：24.

［13］张中杰.地震各向异性研究进展［J］.地球物理学进展，2002，17（2）：281.

［14］MARGETAN F J，THOMPSON R B，ROSE J H et al.The interaction of ultrosound with imperfect interfaces：experimental studies of model structure［J］.J.Nondestr.Eval.，1992，11（3/4）：109.

［15］TONN R.The determination of the seismic quality factor Q from VSP data：A comparison of differen computational methods［J］.Geophysical Prospecting 1991，39（1）：1.

book=123,ebook=123

1001—1749（2012）03—0258—09

P 631.4＋11

A

10.3969/j.issn.1001－1749.2012.03.04

王小杰（1983－），女，博士，现从事地球物理方面的工作。

国家重点基础研究计划（973）项目（2007CB209605）

2011－12－28改回日期：2012－02－24