一种特征融合的带宽自适应Mean Shift跟踪算法
张 良,郑世宝,杨 华
(上海交通大学电子工程系图像通信与信息处理研究所,上海 200240)
运动目标跟踪是当前计算机视觉在图像监控领域的一个研究热点,作为众多跟踪方法的一种,Mean Shift算法是一种基于核密度的无参密度估计算法。从1995年Yizhong Cheng[1]将该算法引入计算机视觉领域便引起了人们极大的关注。早期Comaniciu[2]提出计算目标区域和候选目标区域的颜色直方图特征最大相似度的Mean Shift跟踪算法,采用颜色特征的Mean Shift算法有着旋转不变性且对部分遮挡不敏感,所以Mean Shift算法对非刚体目标在部分遮挡下有着较好的跟踪效果,然而经典Mean Shift算法在目标颜色和背景颜色相近时容易丢失目标。近年来很多背景融合的算法被提出来[3-4],它们综合考虑了颜色特征、边缘特征、纹理特征等。Mean Shift算法的另一个缺陷是核函数是固定的,当目标尺度发生变化时容易跟踪失败,改进的算法参见文献[5-6]。本文在前人的基础上针对Mean Shift这些缺陷提出一种特征融合的核函数带宽自适应算法,首先介绍Mean Shift算法原理,然后提出融合边缘特征、核函数带宽自适应更新算法,在此基础上对目标模型更新进行了相关研究,最后进行实验并给出相关结论及后续工作。
1 Mean Shift目标跟踪算法
Mean Shift目标跟踪算法首先需要确定目标区域,然后初始化目标模型,计算核函数加权的颜色直方图概率分布,以及每一帧中计算候选区域目标模型的直方图分布;计算目标模型和候选模型的Bhattacharyya相似性系数,求得最大相似度的Mean Shift向量,并不断迭代,最终收敛到目标的真实位置。
1.1 目标模型
假设目标区域的中心为x0,xi表示第i个像素点,n为目标区域的像素数,目标模型的概率分布为
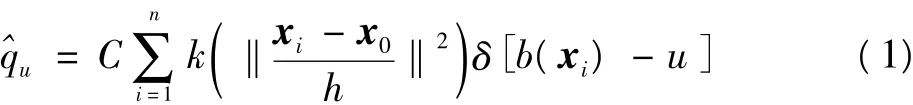
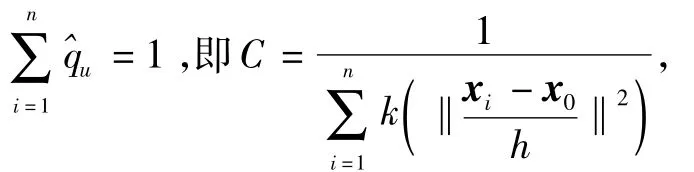
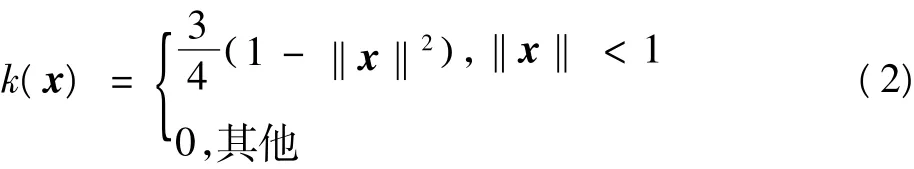
1.2 候选目标模型
候选目标区域以y为中心,核函数的轮廓函数和目标模型相同,候选目标的概率分布为
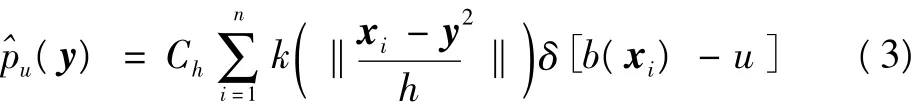

1.3 Bhattacharyya系数
目标模型和候选目标模型对应的颜色直方图的相似性用 Bhattacharyya系数来衡量。Comaniciu[2]论述了Bhattacharyya系数优于其他的相似性函数,其定义为
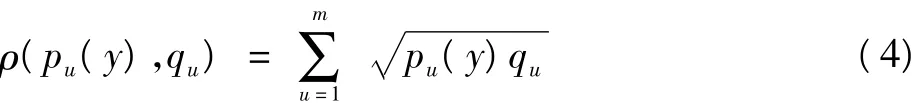
式中:ρ(pu(y),qu)的值越大,表示越匹配,使其最大的候选目标区域即是当前帧中目标的所在位置。对其泰勒级数展开求导为零,推导出Mean Shift向量为

式中:y0是前一帧中的中心位置,不断迭代,计算出最终位置为

2 改进的Mean Shift目标跟踪算法
2.1 背景和运动区域的颜色特征
结合式(1)和式(3),分别可以得到边缘特征的目标模型分布和候选目标模型分布
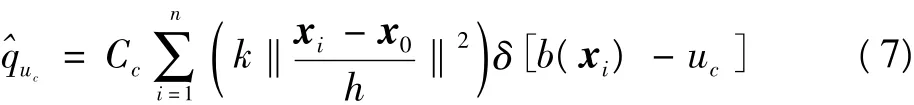
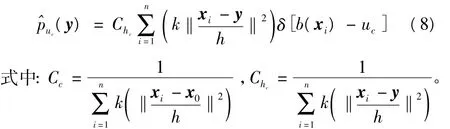
颜色特征的相似性系数为

2.2 边缘特征
首先对图像进行色彩空间变换,转为灰度图像,然后用Canny算子进行边缘检测。当目标区域和背景的颜色很接近时,颜色特征就达不到理想的效果,边缘特征却很适用,公式为

式中:Gh(x,y),Gv(x,y)分别是水平和垂直梯度分量,为了降低噪声对边缘检测的影响,引入阈值T,得到

结合式(1)和式(3),分别可以得到边缘特征的目标模型分布和候选目标模型分布为
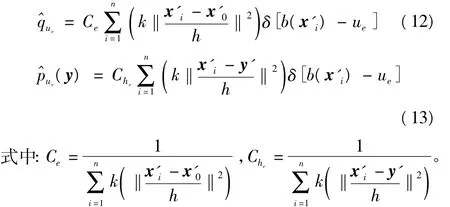
边缘特征的相似性系数为
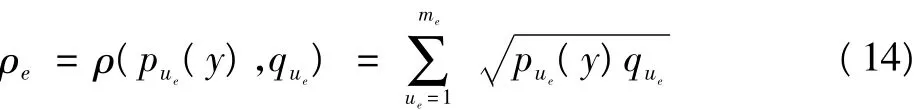
2.3 特征融合相似度



2.4 目标模型更新
运动目标的旋转、背景变化和光照变化等,候选目标模型的颜色特征和目标模型的颜色特征相似度会越来越小,并导致跟踪失败,对目标模型进行更新可以有效避免这种情形。本文尝试在对核函数带宽进行自适应更新的同时,对目标模型进行更新,不过没取得明显效果。本文采用的更新方法是当Bhattacharyya系数大于0.95时,对颜色特征和边缘特征进行下面的更新

式中:t表示第t帧,α代表更新速度,本文中取值0.1。
2.5 跟踪窗口更新[2]
hprev是前一帧的核函数带宽,以hopt=hprev,hopt=hprev+Δh和hopt=hprev-Δh,Δh=0.1hprev,计算这3个窗口下的候选目标模型和目标模型之间的Bhattacharyya系数,取最大系数的hopt,通过下面的公式来更新带宽

式中:更新速度β取值0.1。
3 实验结果
利用Visual Studio 2008在Windows XP,Intel Pentium Dual 1.8 GHz,1.5 Gbyte内存机器上用C语言对经典Mean Shift算法和上述算法进行实验,采用CAVIAR序列[7]中的视频序列,在第510帧时选取目标,选取34×34大小的窗口,取出4帧图像,分别是第512,718,824和918帧。经典Mean Shift算法的结果见图1,融合边缘特征的改进算法的结果见图2,融合边缘特征的核函数带宽自适应算法的结果见图3,融合边缘特征的目标模型自适应更新、核函数带宽自适应算法的结果见图4。对比图1和图2,经典Mean Shift算法逐渐偏离目标的真实位置,改进算法跟踪得非常准确,在第912帧时,目标颜色特征和背景颜色特征非常接近,经典Mean Shift算法已经跟踪失败,而融合颜色、边缘特征的改进算法依然准确跟踪目标,具有非常好的稳健性。通过对比图3和图2可以看到,核函数自适应算法由于少了背景信息的干扰,能更精确地跟踪目标。

图1 基于颜色特征的Mean Shift算法

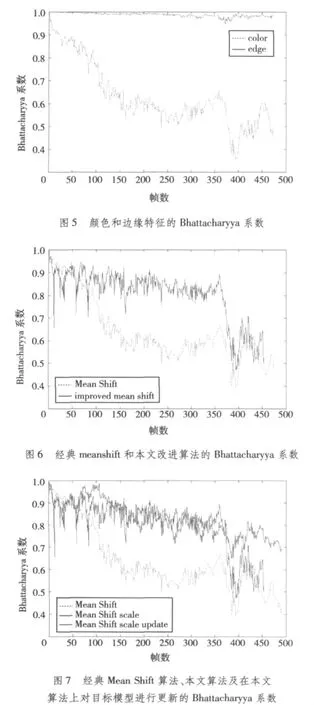
图5~图7的横轴表示帧数,纵轴表示Bhattacharyya系数,从图5可以发现,在目标背景边缘特征不明显的情景下,边缘特征的Bhattacharyya系数远大于颜色特征的系数。一方面由于边缘特征的存在,另一方面,由于核函数自适应消除了多余的背景,所以从图6可以看到改进算法的Bhattacharyya系数明显高于经典算法。通过图4和图7不难发现,在本文算法的基础上,对目标模型进行更新,其Bhattacharyya系数比本文算法更趋平稳,但跟踪效果在很多地方却没有本文算法更新得准确。
4 结论及展望
基于颜色特征的Mean Shift算法容易在目标颜色特征和背景颜色特征相似的情形下失效,本文在前人提出的融合边缘特征的基础上进一步进行了核函数带宽自适应的研究,取得了不错的效果,使得跟踪效果更精确。对目标模型进行更新的效果不是特别好,将在今后进一步探索在保证跟踪效果的前提下如何对目标模型进行有效更新。
:
[1]CHENG Y.Mean Shift,mode seeking and clustering[J].IEEE Trans.Pattern Analysis and Machine Intelligence,1995,17(8):790-799.
[2]COMANICIU D,RAMESH V,MEER P.Kernel-based object tracking[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2003,25(5):564-577.
[3]BABAEIAN A,RASTEGAR S,BANDARABADI M,et al.Mean Shiftbased object tracking with multiple features[C]//Proc.41st Southeastern Symposium on System Theory,2009.Tullahoma,TN:[s.n.],2009:68-72.
[4]ZHANG Xiang,DAI Yuanming,CHEN Zhangwei,et al.An improved Mean Shift tracking algorithm based on color and texture feature[C]//Proc.2010 International Conference on Wavelet Analysis and Pattern Recognition(ICWAPR).Qingdao,China:[s.n.],2010:38-43.
[5]COLLINS R T.Mean-Shift blob tracking through scale space[C]//Proc.2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.[S.l.]:IEEE Press,2003:18-20.
[6]YILMAZ A.Object tracking by asymmetric kernel Mean Shift with automatic scale and orientation selection[C]//Proc.IEEE Conference on Computer Vision and Pattern Recognition,2007. [S.l.]:IEEE Press,2007:1-6.
[7]FISHER R.CAVIAR test case scenarios[EB/OL].(2007-10-26)[2010-03-01].http://homepages.inf.ed.ac.uk/rbf/CAVIARDATA1/.

