J-C模型下双腔双原子的量子纠缠研究

陈作鹏，胡占宁，成耀宇，高进然

（天津工业大学理学院，天津 300387）

J-C模型下双腔双原子的量子纠缠研究

陈作鹏，胡占宁，成耀宇，高进然

（天津工业大学理学院，天津 300387）

文章选取J-C模型，在此模型下引入双腔双原子体系。考虑这两个原子的纠缠问题，通过泰勒展开计算出此体系中的量子关联concurrence，并最终推导出关于concurrence的方程，这个方程很好地预测了自旋1/2量子纠缠的产生与坍塌。

量子纠缠；泰勒展开；量子关联

1 J-C模型的哈密顿量

我们知道，J-C模型[1]的哈密顿量为：

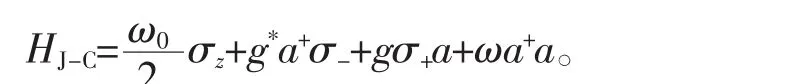
其中，ω0是两能级原子之间的转移频率，g是原子和场之间的耦合常熟，ω是单模场的角频率，σz，σ+，σ-是描述原子的一般泡利矩阵，

首先推导出J-C模型的本征态，据下式：

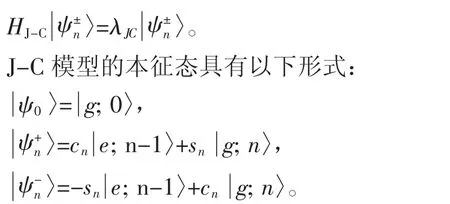
其中，g为基态，e为激发态，

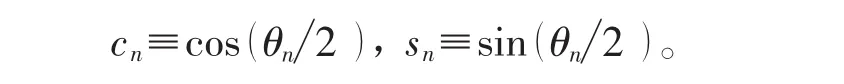
在这里，转动角θn可以用布洛赫球的极角来定义，它的一般形式为：

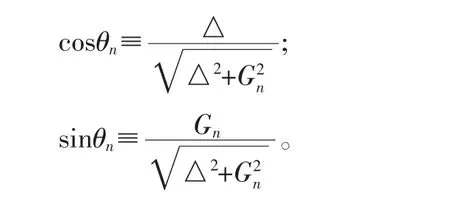
由以上所知，可以进行以下推导：假设HJC的本征值是λ，则有

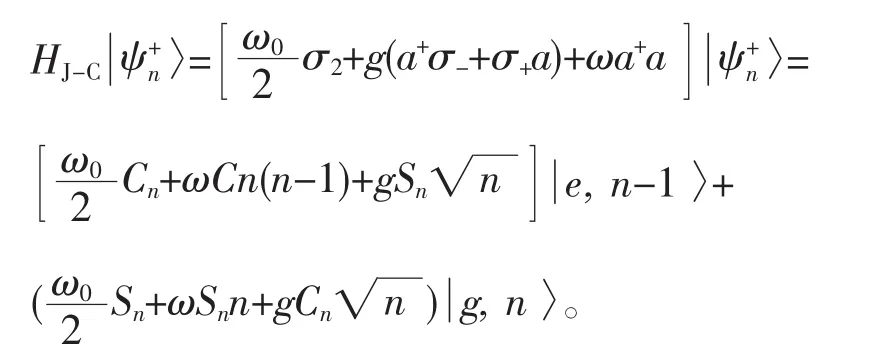
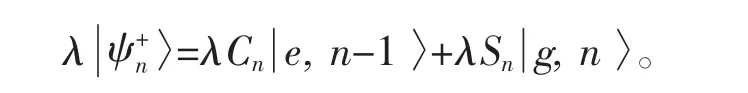
有上面两个式子可以得到

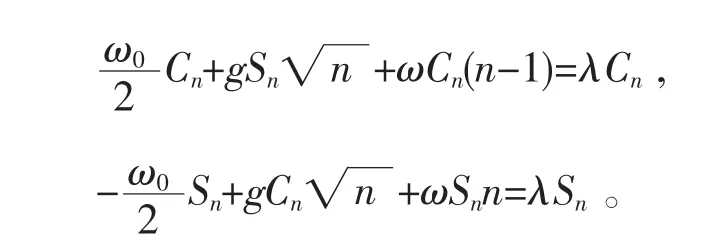
整理得

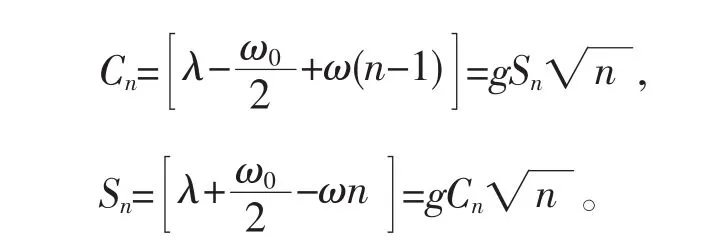
两式交叉相除

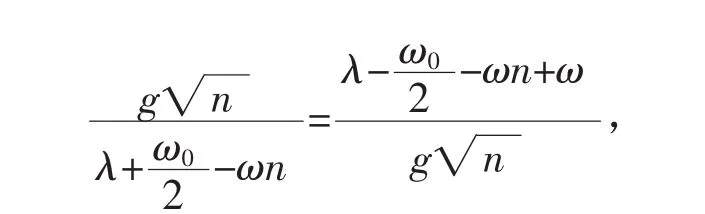
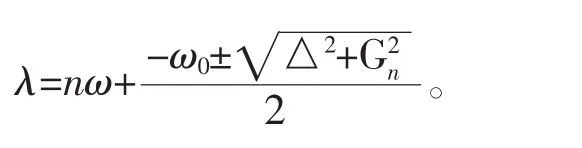
得HJC的本征值为

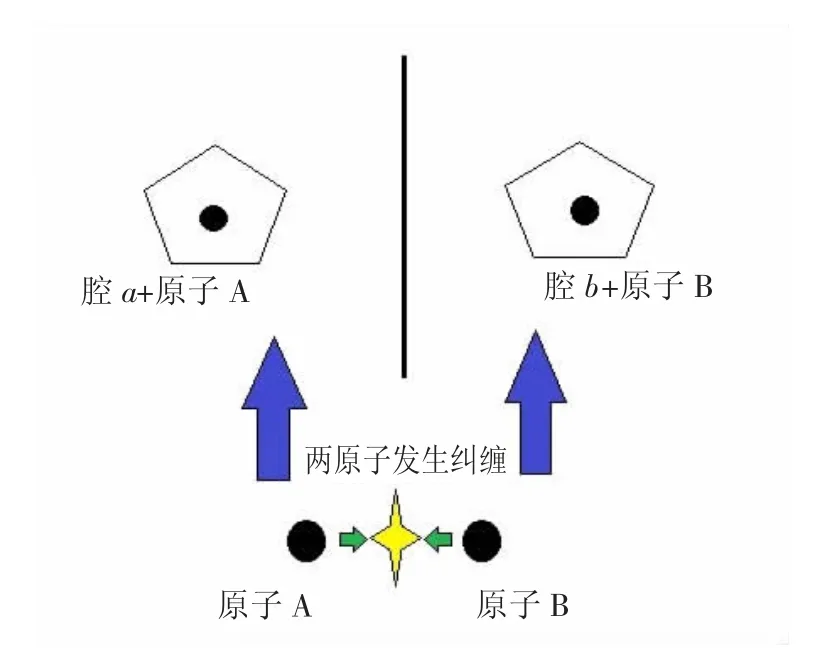
图1 双腔双原子作用示意图

本文我们选取双腔双原子作为模型。在这个体系中，如图1所示，原子A和原子B首先发生纠缠现象，然后分别被安置在各自的腔中（腔a和腔b），在此之后，只有原子A与腔a，原子B与原子b存在相互作用，原子A与原子B之间的纠缠不会收到外界的干扰[3-5]。

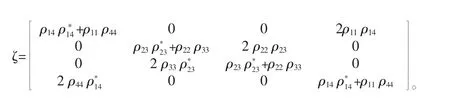
这个辅助矩阵ζ的4个本征值，分别为

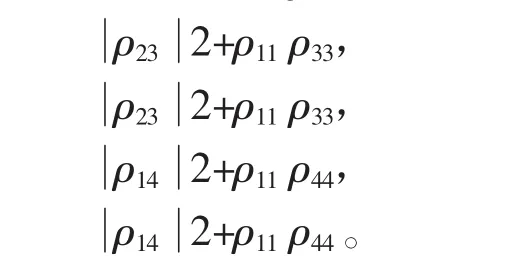
由此我们可以计算出，

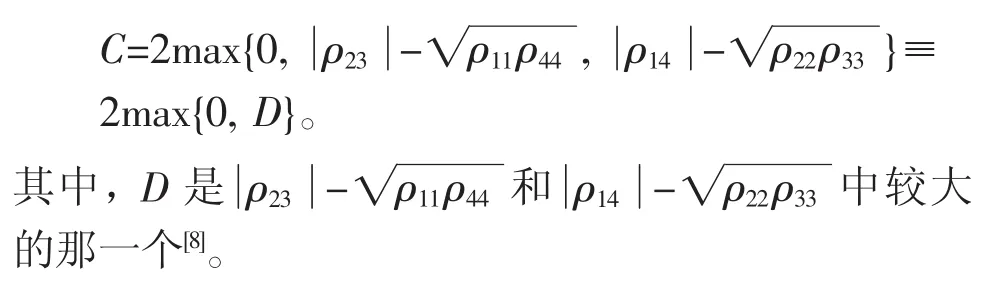
2 双腔双原子的J-C模型下计算系统的concurrence

假设初态为叠加的贝尔态

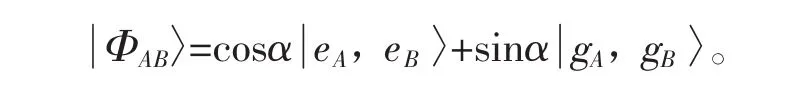
很容易看出来，α=±π/4α=±π蛐4，原子与腔耦合的初态为

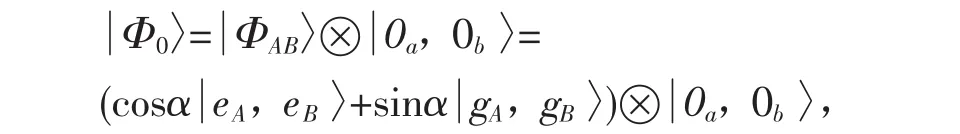
3 成对量子纠缠的测量

在Wootters＇的论文[6]中提出了concurrence的概念，当1≤C≤0，当C=0时代表了没有纠缠现象存在，C=1表示最大纠缠态。C的简易表达式为

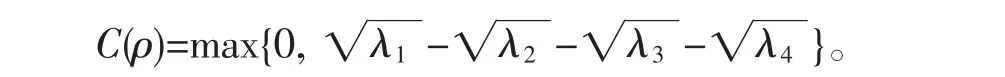
在这个等式里λi代表了辅助矩阵的本征值的降序排列，辅助矩阵表达式为

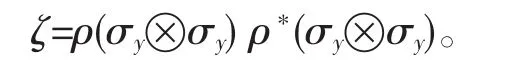
ρ*为密度矩阵ρ的复共轭，σy为标准形式的泡利矩阵。

在两个量子比特的形式下，密度矩阵为X行矩阵[7]，在这种矩阵中，只有对角线和反对角线上的元素不为0。

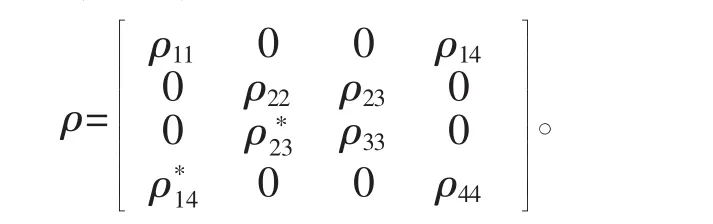
在这里

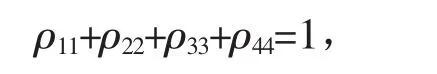
有

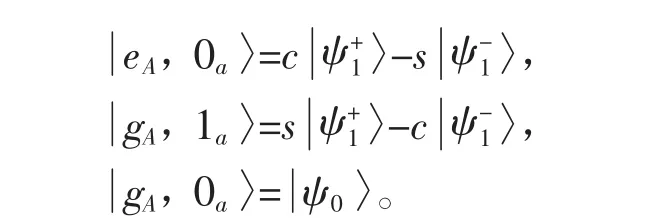
因此，原子与原子纠缠的初态形式如下：

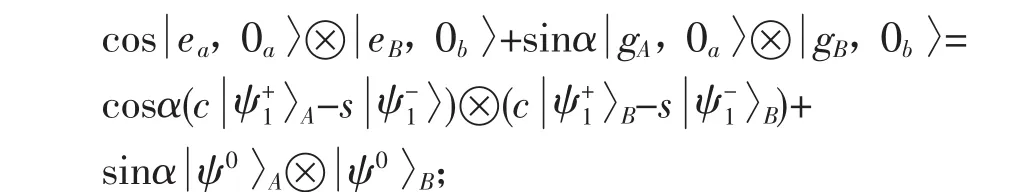
随时间演化的缀饰态为：

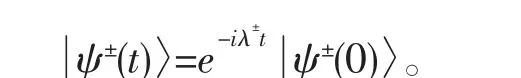
在此，设

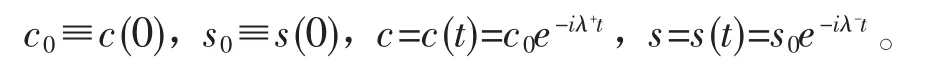
此处的

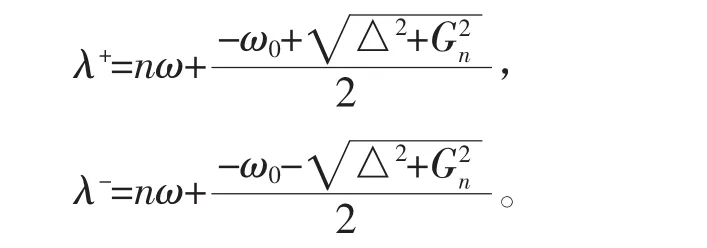
我们写出随时间演化的函数：

有上式，我们可以计算出系统的密度矩阵

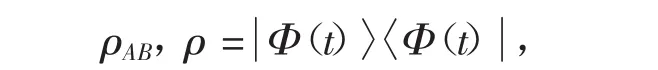
对ρ约化得，

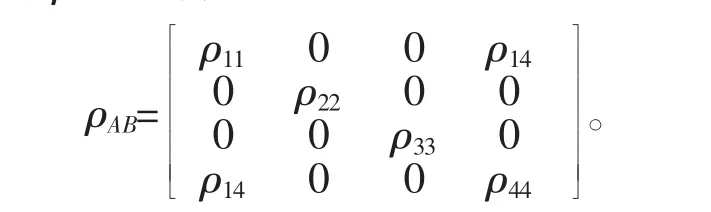
这个密度矩阵的concurrence为，

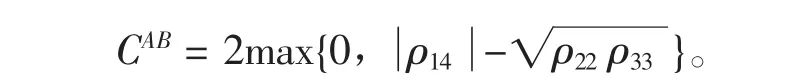
经计算得到：

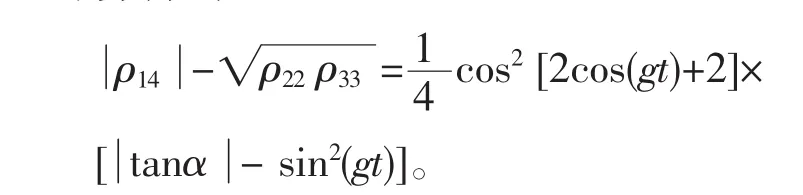
假设CAB=2max{0，DAB}，

其中，

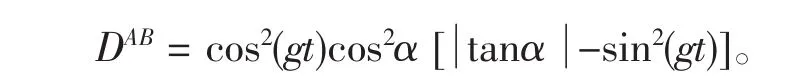
由上式，我们可以预测出此体系下纠缠的“突然死亡”和“再生”，如图2、图3所示。

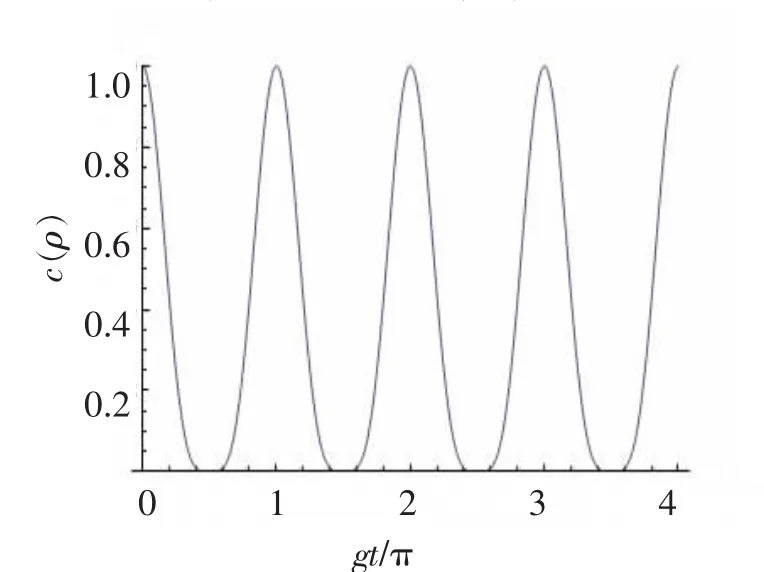
图2 当α＝π/4时，c（ρ）随时间t的变化

当α＝π/4时，

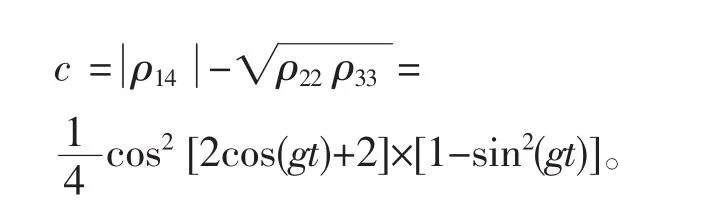
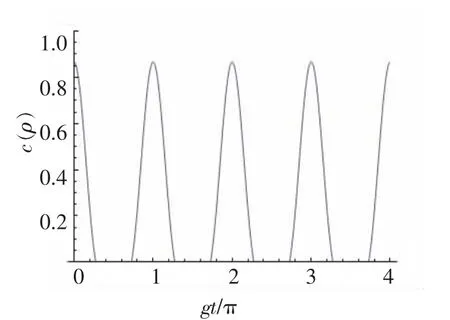
图3 当α＝π/6时，c（ρ）随时间t的变化

当α＝π/6时，

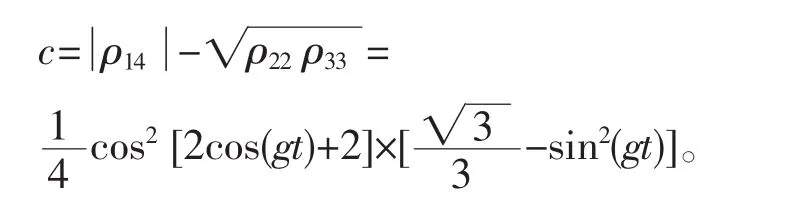
4 结论

通过推导出来的公式，可以预测不同α值对应的量子纠缠的“突然死亡”和再生，当α＝π/6时我们发现这个体系下的量子纠缠开始出现“突然死亡”，如图3所示。图像开始出现零以下的部分，这种现象就叫做量子纠缠的“突然死亡”。随着时间的演化，图像又会出现回到零以上的部分，这种现象我们称为量子纠缠的“再生”。

总之，通过对双原子双腔J-C模型的分析，我们得到了以上结论。希望我们的结论能对量子纠缠理论研究做出一点贡献。

[1]Jaynes E T，Cummings Proc FW.Comparison of quantum and semiclassical radiation theorieswith application to the beam maser [J].IEEE，1963（51）：89-109.

[2]钱伯初.量子力学[M].北京：高等教育出版社，2006：34-46.

[3]RempeG，WaltherH，Klein N.ObservationofQuantum Collapseand RevivalinaOne-AtomMaser[J].PhysRev Lett，1987（58）：353-356.

[4]Brune M，Schmidt-Kaler F，Maali A，etal.Quantum RabiOscillation：A Direct Testof Field Quantization in a Cavity[J].Phys Rev Lett，1996（76）：1800-1803.

[5]Boca A，Miller R，Birnbaum KM，etal.Observation of the vacuum RabiSpecturm for One Trapped Atom[J].Phys Rev Lett，2004（93）：233603-1-233603-4.

[6]WoottersW K.Entanglementof Formation of an Arbitrary State of Two Qubits[J].Phys Rev Lett，1998（80）：2245-2248.

[7]Yu T，Eberly JH.Robustness of Quantum Discord to Sudden Death[J].Quantum Inf Comput，2007（7）：459-461.

[8]Yu T，Eberly JH.Sudden Death of Entanglement[J].Science，2009（323）：598-601

〔责任编辑 李海〕

The R esearch of D ouble-cavity and D ouble-atom Q uantum E ntanglementunder J-C M odel

CHEN Zuo-peng，HU Zhan-n ing，CHENG Yao-yu，GAO Jin-ran
（School of Science，Tianjin Polytechnic University，Tianjin，300387）

In this article we select the J-Cmodel，then introduce the double-cavity and double-atom system in thismodel，and consider this two-atom entanglement，using the Taylor expansion to calculate the quantum correlations concurrence in this system and eventually deduce a equation about the concurrence，which predict s the sudden death and the rebirth of the spin quantum entanglement.

quantum entanglement；Taylor expansion；quantum correlations

TP15

A

1674-0874（2012）03-0029-03

2012-03-25

陈作鹏（1988-），男，甘肃兰州人，硕士研究生，研究方向：量子信息。