基于纯各向异性扩散和四阶PDE 的混合去噪方法研究

乔林峰，王 俊

(陆军军官学院，安徽 合肥 2300311)

近年来，关于利用偏微分方程方法进行图像处理方面的研究已在多个不同领域显有成效，在图像去噪、图像分割、图像复原等方面都提出了很多经典模型及算法.这些模型在图像处理方面都取得了非常不错的成绩.

本文针对四阶PDE模型过多损失边缘信息和纯各向异性扩散模型在平滑区域产生阶梯效应的缺点，提出了一种新的模型.该模型适用于去除高斯噪声和椒盐噪声，并在有效去除噪声的同时，既抑制了阶梯效应又很好地保持了图像的边缘和纹理细节信息，同时该模型的算法实现简单，稳定性也很好.

1 纯各向异性扩散模型

Perona和Malik于1990年在文献［1］中提出了P－M扩散方程:

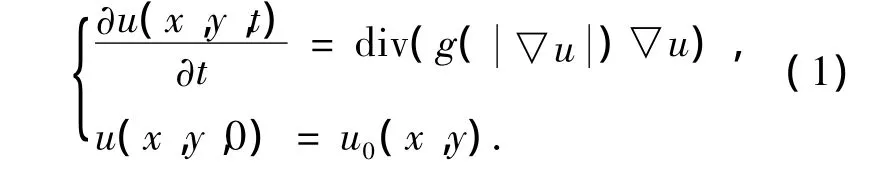
该方程在图像去噪的过程中能很好保持边缘信息.式中g称为传导函数，一般取为:

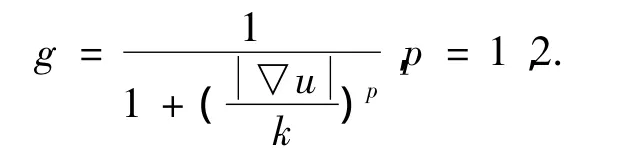
式中，k为一临界参考值.

图像处理的很多应用领域对该模型在图像特性信息的保护作用都有所关注，然而该模型的初值问题可能会出现“病态”问题［2］，同时，该模型对椒盐类噪声和强边缘附近的其它噪声的处理不是很好.

Alvarez和Morel对P－M扩散方程进行了改进，并提出了一种“纯”各向异性扩散方程［3］:

进一步，有:

这样，方程(2)的扩散项转化为ξ方向上的扩散项.在运算过程中，为了避免图像中平坦区域的梯度值可能为零，该模型采用了参数提升梯度，即

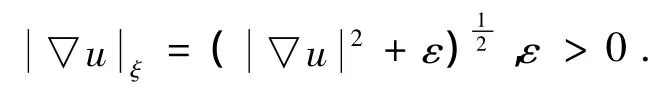
进一步，利用有限差分格式对方程(2)进行离散化，令迭代次数为k，空间步长为h，时间步长为 Δt，u(i，j)=ui，j，u0(i，j)=u0i，j，则

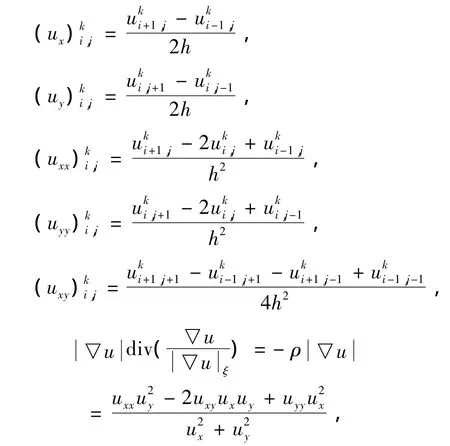
得该方程的离散显示差分方程为:

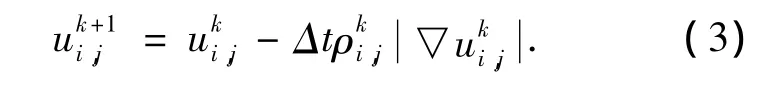
该模型扩散只是沿着垂直于图像的梯度矢量方向进行，可以看出其具有较强的边缘保护和去除椒盐类噪声的能力.

2 四阶PDE图像去噪模型

Yu－Li和 M.Kaveh等人在文献［4］中提到了一个四阶PDE.此方程克服了低阶PDE在图像处理中存在的一些缺点，既有效保持了去噪的效果，又在一定程度上保持了图像的细节和纹理特征.方程如下:

其中，f是正的非增函数，文献中取其为:

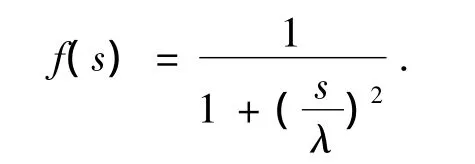
其中λ为常数.

在这里，我们仍采用有限差分格式对其离散化.令迭代次数为k，空间步长为h，时间步长为Δt ，u(i，j)=ui，j，u0(i，j)=u0i，j，则得到该四阶PDE的显示差分格式为:

该四阶PDE模型能避免产生“阶梯”效应，并能在很大程度上恢复和保护平滑区域信息和细小纹理.

3 基于纯各向异性扩散和四阶PDE的混合模型

3.1 模型提出

针对以上纯各向异性扩散模型和四阶PDE模型在图像去噪的特点讨论，我们提出了混合的偏微分去噪模型:

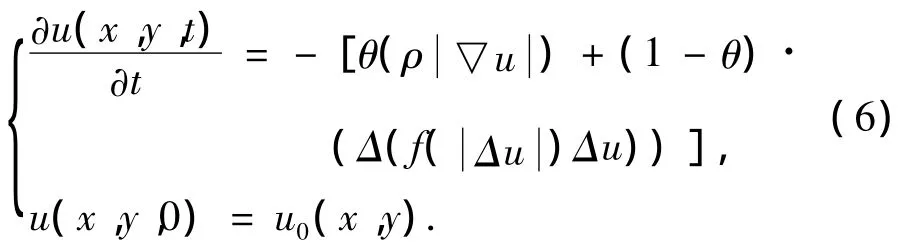
式中，θ∈［0，1］为权重函数.设m，n分别为纯各向异性扩散模型和四阶PDE的解，则凸组合

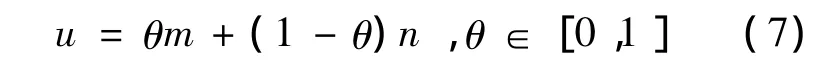
即为(6)式的解.由图像处理的实际情况可知，对于边缘和平坦区域，应突出纯异性扩散的作用，故θ应趋于1;对于渐变区域，应突出四阶PDE的作用，故θ应趋于0.所以，权函数的递归表达式我们构造如下:

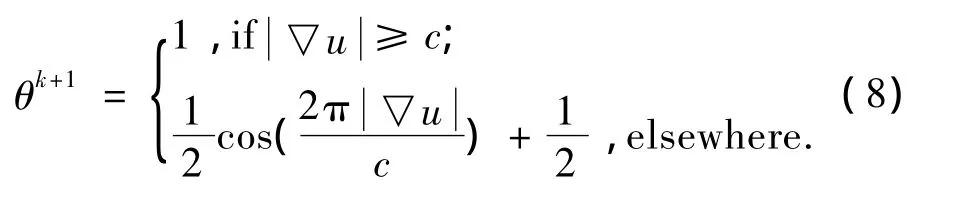
其中u=θkm+(1-θk)n，c为正数.

3.2 求模型的数值解

本文所提出的模型数值解的算法步骤为:

1)初始化:令 θ∈［0，1］，c和 p(收敛精度)，记m0=ur，n0=ur，其中ur为加入了混合噪声的图像，其大小为M×N.

2)循环计算:k=0，执行如下过程.

3)根据(3)式计算

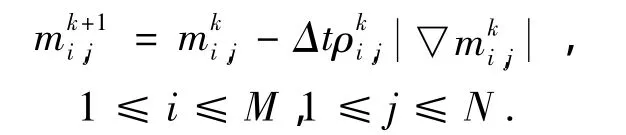
4)根据(5)式计算

5)根据(8)式计算θk+1.

6)根据(7)式进行凸组合:uk+1= θk+1mk+1+(1- θk+1)nk+1.

7)mk+1=uk+1，nk+1=uk+1.

9)结束.

4 仿真实验及其结果分析

为了有效验证本文的方法，测试对象我们选取了256×256的图像，对本文提出的混合模型以及四阶PDE模型和纯各向异性扩散模型在不同强度的高斯噪声、椒盐噪声下的去噪效果进行了仿真实验并做了比较.在这里，我们用信噪比(SNR)和归一化的均方误差(NMSE)作为其评价指标:

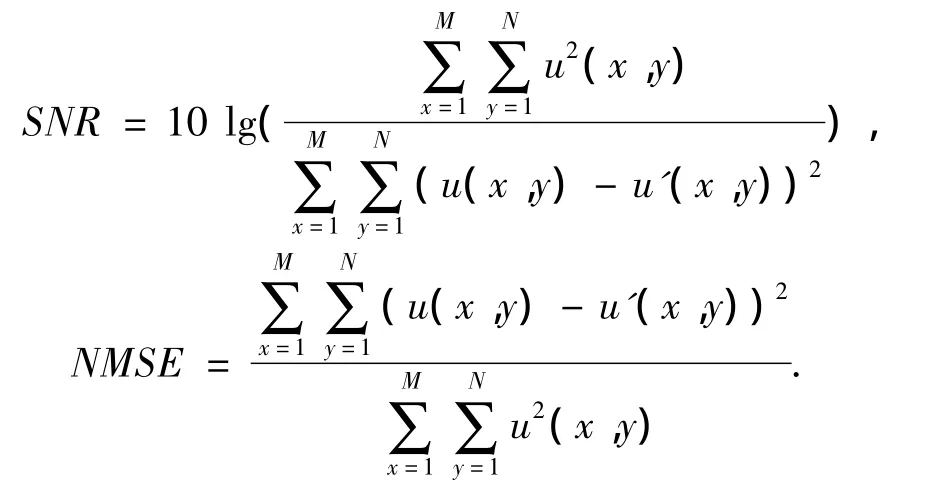
u(x，y)和u'(x，y)分别代表处理前的图像和处理后的图像.

利用数学软件Matlab，我们对原始图像添加了方差为0.02的高斯噪声和密度为0.1﹪的椒盐噪声，然后用纯各向异性扩散模型、四阶PDE模型和本文混合去噪模型进行了去噪处理.三种模型的去噪效果比较图如图1所示.

图1 三种模型的去噪效果比较图

从图1可以看出，纯各向异性扩散模型尽管对混合噪声去除得比较彻底，但图像的纹理细节却受到较大破坏，与原始图像中的河流和街道区域进行对比可以发现，有一部分的细节信息已经丢失;四阶PDE模型虽然对图像的纹理细节起到了一定程度的保护，但图中仍残留着去噪后留下的一些麻点和椒盐噪声，对视觉效果有一定的影响.本文提出的混合去噪模型，既对椒盐噪声和高斯噪声起到了很好的抑制，又保持了原始图像中的细节信息和大量纹理.

与此同时，我们在测试图像中分别加入4种不同强度的高斯和椒盐混合噪声，再利用纯各向异性扩散模型、四阶PDE模型以及本文提出的混合去噪模型进行处理，然后对去噪后图像的归一化均方误差和信噪比进行统计(见表1)，其中M表示椒盐噪声密度，F表示高斯噪声方差.从表1中数据可以看出，本文提出的算法对于处理加入不同强度噪声的图像，客观效果均好于其他两个模型，且算法的稳定性也比较好.

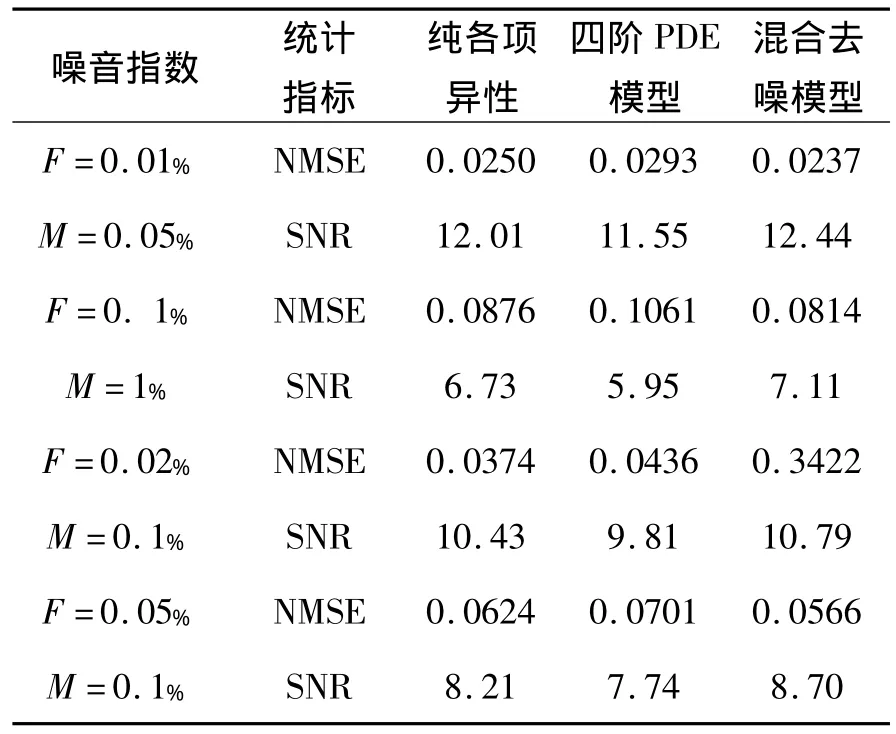
表1 三种模型处理图像中不同混合噪声的归一化均方误差和信噪比统计比较

［1］Perona P，Malik J.Scale － space and edge detection using anisotropic diffusion［J］.IEEE Transactions on Pattern Analysis Machine Intelligence，1990，12(7):629－639.

［2］Catte F，Lion J，Morel M.Image selective smoothing and edge detection by nonlinear diffusion［J］.SIAM Journal on Numerical Analysis，1992(29):182 －193.

［3］Alvarez L，Morel JM.Formalization and computational aspects of image analysis［M］.United States of America:Cambridge University Press，1994:1 －59.

［4］Whitaker R，Pizer S.A multi－ scale approach to nonuniform diffusion［J］.Computer Vision，Graphics，and Image Processing:Image Understanding，1993，57(1):99－110.

［5］张亶，陈刚.基于偏微分方程的图像处理［M］.北京:高等教育出版社，2005.

［6］陆君安，尚涛，谢进，等.偏微分方程的 Matlab解法［M］.武汉:武汉大学出版社，2004.

［7］冈萨雷斯.数字图像处理:第2版［M］.北京:电子工业出版社，2002:1－3.

［8］陈祖墀.偏微分方程［M］.合肥:中国科学技术大学出版社，2002.