基于小波变换的齿轮箱故障诊断*

徐英帅，王细洋，孙 伟

(南昌航空大学航空制造工程学院，南昌 330063)

基于小波变换的齿轮箱故障诊断*

徐英帅，王细洋，孙 伟

(南昌航空大学航空制造工程学院，南昌 330063)

时域同步平均(Time Synchronous Averaging，TSA)信号只包含齿轮啮合频率信号和倍频信号，若齿轮出现故障，会使TSA信号得到某种程度的调制。文章将连续小波变换应用于齿轮箱振动采样的TSA信号，检测和分析齿轮箱的轮齿缺陷，设计并制作齿轮箱故障诊断试验台，通过齿轮全运行周期啮合试验，利用LABVIEW虚拟仪器采集系统采集振动信号，然后利用MATLAB编写相应的程序，绘制出所需信号的波形图，对所采集的数据文件进行信号分析处理，以达到齿轮箱故障诊断的目的，并验证了小波变换对齿轮故障诊断的有效性。

故障诊断;齿轮箱振动;TSA信号;连续小波变换;信号分析处理

0 引言

齿轮箱是各类机械的变速传动装置，齿轮箱的运行状态是否正常，直接影响整台机器或机组的工作。据统计，在齿轮箱中，齿轮本身的故障比率最大，占60%左右［1-2］，可见齿轮箱中齿轮本身的制造和装配质量以及运行维护是关键。齿轮传动是机械设备中最常用的传动方式，在航空器、大型重载机械等方面应用广泛，齿轮失效又是诱发其故障的重要因素。在生产中，由于小故障未能及时发现而酿成设备事故，造成经济损失的事件屡见不鲜。因此对齿轮运行状态进行在线监测和故障诊断对降低设备运行费用、防止突发事故具有重大的现实意义。齿轮的故障常在振动状况方面体现出来，因此振动信号监测是齿轮故障诊断的主要手段，小波作为一种新的信号处理方法，是较好的时-频域信号分析方法，在齿轮振动信号分析中得到了广泛的应用。本文将连续小波变换应用于齿轮箱振动采样的TSA信号，检测和分析齿轮箱的轮齿缺陷，得到了很好的效果，证实了小波变换对齿轮故障诊断的有效性。

1 理论基础

1.1 齿轮故障机理

齿轮可看做是由轮齿和轮体组成的振动系统。在润滑良好且齿面摩擦度低的情况下，齿面上摩擦力的作用常可忽略，此时齿轮副的振动方程可以表示为［2-4］:

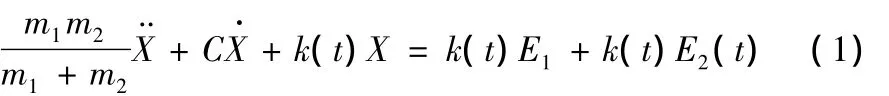
式中，m1和m2分别是齿轮副中主动轮与从动轮的质量，X是沿作用线上齿轮的相对位移，C是齿轮啮合阻尼，k(t)是啮合刚度，E1是齿轮受载后的平均静弹性变形，E2(t)是故障函数。等式的前端代表齿轮副本身的振动特征，后端代表激振函数。

由于激振函数中k(t)是周期性的变量，因此齿轮在无故障的理想情况下也存在振动，这样的振动称为啮合振动。该振动是以每齿啮合为基本频率的，即啮合频率，其计算式可以表示为:

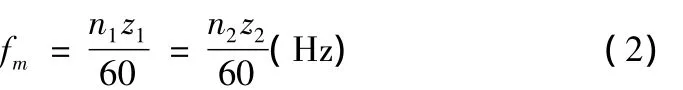
式中，n1、n2是齿轮副中主、从动轮的转速，z1、z2是主、从动轮的齿数。一般情况下，由于k(t)不是标准正弦函数，因此啮合振动中还含有fm的谐波分量。激振函数中k(t)E2(t)是导致齿轮振动异常的激励源。诊断齿轮故障的任务在于检测出由故障激励源所造成的异常振动的特征。一般情况下，齿轮失效之后，由于振动信号的特征既有幅值调制又有相位调制，因此齿轮振动信号的数学模型可以表示为:

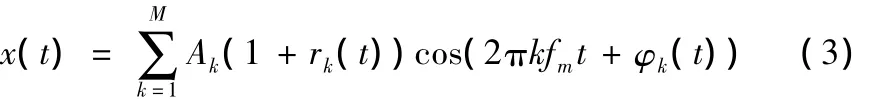
其中，rk(t)和φk(t)分别是调幅信号与调相信号。对于没有任何缺陷的齿轮，也不会有调制现象;当齿轮出现异常时，就会出现调制现象，并且随着缺陷的加剧，调制也会越深。

1.2 时域同步平均

时域同步平均法是齿轮故障诊断中信号预处理的一种常用方法。对指定齿轮箱旋转振动信号进行同步采样，如果能保证不同时刻采集信号的起始点相位一致，并保证采样频率与采集的点数一样，这样的时域信号不但可以平均，而且还可以大大的提高指定周期信号的信噪比，并能减少或抑制不相干的振动信号成分，进而只提取相关的振动信息，这种方法称为时域同步平均(Time Synchronous Averaging，TSA)［4］。概括的讲就是从齿轮振动中取出啮合频率成分，并将它与齿轮轴的旋转频率同步相加、平均，是从混杂有噪声干扰的信号中提取周期性分量的有效方法。

时域同步平均展示了齿轮箱旋转超过一转时齿轮啮合振动的形式，包括一些调制的影响，同时它的频谱还包含相关齿轮啮合成分与边频带簇。因此，时域同步平均可以表示为［5］:

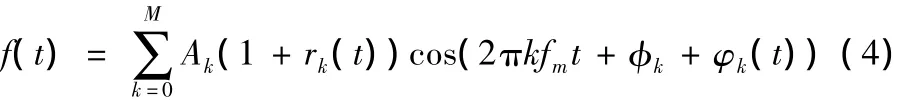
式中，M是齿轮啮合谐波频率的阶数，fm是齿轮的啮合频率，Ak与φk分别是k阶啮合谐波频率的振幅与相位。相同谐波频率调制的影响包括振幅调制与相位调制，其中1+rk(t)是振幅调制函数，φk(t)是相位调制函数，伴随着齿轮的旋转频率这些调制函数是周期性的。只有当齿轮故障的出现频率与转动频率同步时，时域同步平均法才可以增强故障信号，而不起抑制信号的相反作用。齿轮的轮齿破损与齿轮轴破损都属于这类信号，故可采用时域同步平均法。随着平均次数的逐渐增加，齿轮旋转频率与啮合频率及其各阶倍频成分被保留，而其他轴的振动信号和噪声部分相互抵消趋于消失，由此便可得到仅与被检测齿轮振动有关的信号。

1.3 连续小波变换

由于离散小波分析具有信息遗失、对小波基函数要求严格等缺陷，而连续小波分析没有这些缺陷，因此本试验采用连续小波变换的方法。如果ψ(T)∈L2(R)，其中ψ(t)为平方可积函数，L2(R)为R上平方可积函数构成的函数空间，ψ(t)的傅里叶变换为(ω)满足容许性条件［6-7］:

则称ψ(t)为母小波。将母小波ψ(t)经过伸缩和平移，便可得到一小波序列:

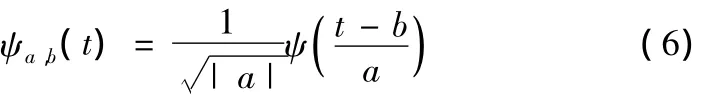
式中，a，b∈R且a≠0，a为伸缩因子(尺度因子，表示与频率相关的伸缩)，b为时间平移因子，称ψa，b(t)为连续小波基函数。若将任意L2(R)空间中的函数f(t)在小波基下展开，则称此种展开为函数f(t)的连续小波变换(Continuous Wavelet Transform，CWT)，表达式如下［8-9］:

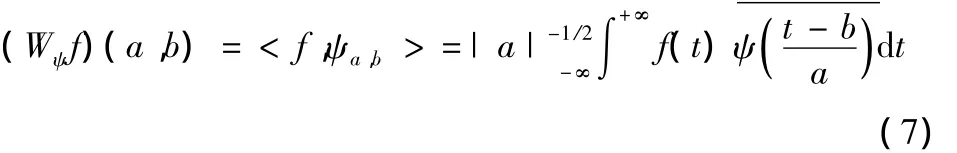
小波变换系数的大小实际上反映了信号局部与各小波基函数的相似程度，系数越大，表明信号局部与对应的小波基函数越相似。选择小波基函数时，应尽量使小波基函数波形与齿轮故障信号引起的脉冲波形相似。Morlet小波符合这样的要求，在故障诊断中也得到了广泛采用。以下是Morlet小波函数的定义:

式中，fb是带宽频率，fc是小波中心频率。Morlet小波的重要特征之一是其傅立叶变换是高斯函数。选择合适的带宽频率和中心频率，依赖于所分析的信号。

2 试验研究

齿轮箱故障诊断试验装置为二级齿轮变速箱试验台(如图1所示)。齿轮箱由交流电动机驱动，该电动机的同步转速为1.75kr/min，额定功率为4.5kW，并且带动同样规格的由电动机改装而成的发电机作为负载。通过控制负载发电机的电流，来获得齿轮变速箱不同的负荷状态。由于发电机的额定功率比齿轮箱的额定功率要大，使得齿轮超负荷运行，寿命缩短，这样有利于对齿轮作全生命周期振动信号的分析。试验台运行时发电机的电流反馈给电动机，以提高能源的利用率。

图1 齿轮箱故障诊断试验台

利用LABVIEW虚拟仪器平台建立数据采集系统。该系统的采样频率为20kHz，每10min采样一次，每次采样10s，采集的信号经A/D转换后，按一定格式转换成数据文件存储到硬盘里。每一个数据文件含有2×105个采样点。齿轮变速箱上放置加速度式振动传感器、脉冲信号发生器、扭矩传感器以及速度传感器。由于齿轮径向传感器采集的信号对齿轮破损最为敏感，因此把它作为研究对象。本试验所使用的齿轮副传动比为1:3.333，主动轮是齿数为21的整体齿轮轴，从动轮齿数为70，齿轮的啮合频率为613Hz。

对齿轮箱进行全生命周期破损试验，整个试验分两个阶段，共运行约114.3h。第一阶段从正常齿轮开始进行啮合试验，齿轮箱在满负荷的条件下运行约95h;第二阶段通过改变负载发电机的电流来逐渐提高齿轮箱的负荷，以加快齿轮的破损，直到无法继续运行，该阶段运行约19.3h，此时齿轮状态为从动轮有5个轮齿完全断裂，2个轮齿部分破裂(如图2所示)。整个试验总共采集数据文件340个，其中有效文件323个。

图2 齿轮轮齿破损情况

3 试验结果与分析

从加速传感器获得的信号被以一定的时间间隔重复采样，相当于齿轮的相位是不变的。在齿轮旋转时，每发生一次啮合就会产生一个脉冲信号。在振动信号的获得与数据处理的过程中，排除由齿轮速度波动引起的故障，以及在每个周期内提供数据大小相同的样本是十分必要的。对重复采样的信号进行时域同步平均获得信号f(t)，并对信号f(t)进行连续小波变换，然后利用Matlab高级程序设计语言编写相应的程序，对所采集的数据文件进行分析处理，绘制出所需信号的波形图，通过图像分析与对比便可得出故障信息，以达到齿轮箱故障诊断的目的。

数据文件000是所采集的第一个数据文件，此时的齿轮处于正常状态，图3a和b是其原始信号和频谱图。设主动齿轮转速为v，采样频率为f，每转点数为n，则有:

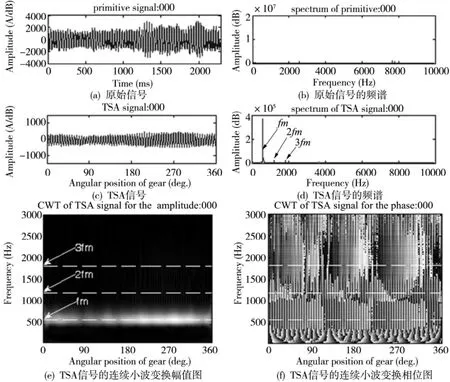
图3 数据文件000的振动信号

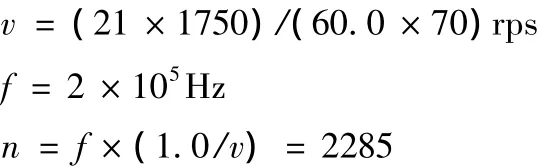
现将每个文件中的数据以2285个点为一段截取，再将每段对应点同步相加最后平均，便可得到时域同步平均信号，即TSA信号，图3c和d是数据文件000的TSA信号和频谱图。在利用连续小波变换进行分析时，分析频带选为100～3000Hz，此时可以包括所有重要啮合谐波(1st谐波fm=613Hz，2st谐波2fm=1226Hz，3st谐波3fm=1839Hz)。中心频率和带宽参数通过连续小波变换分析实验分别确定为1和0.5Hz。用连续小波变换得到的图都是时间尺度上的，通过关系式f=f0/a将尺度与频率进行转换，并将时间转换成齿轮的旋转角度，这样连续小波变换的结果将以旋转角度-频率图的形式给出，图3e和f是数据文件000的TSA信号的连续小波变换幅值图和相位图。

图3a为齿轮箱振动信号的时域波形，由于存在噪声与干扰信号，因此波形不是很光滑，存在波动，而且周期性信号不是很清晰。原始信号经时域同步平均得到如图3c所示信号，与原信号相比，新信号波形得到了很大改善。从TSA信号图中可以明显的看到70个波峰和70个波谷对应70次的啮合，与图3a相比该波形光滑，说明经时域同步平均后，信号中强烈的干扰已基本被排除。再观察图3d中TSA信号的频谱，可以看到主要频率分量fm=613Hz，即啮合频率，同时也存在2阶频2fm=1226Hz，及3阶频3fm=1839Hz，与图3b相比可看出高频噪声已基本消除。TSA信号的连续小波变换幅值图相当于对齿轮旋转一整转的信号进行分析，图中三条虚线分别对应齿轮啮合频率以及2次、3次谐波。从图3e可以清楚的看到振动信号大多数的能量集中在齿轮啮合频率fm=613Hz的位置，也可以看到在啮合频率处的能量会有细小的波动，这些小的波动是正常的，是由于实际的齿轮并不完满，齿轮本身还存在一些小的瑕疵，以及所分析的是实验采集的数据等原因引起的。TSA信号的连续小波变换相位图中也有一些小的波动，这些波动也是正常的。需要注意的是相位比幅值更加敏感，观察图3f可以看到在频率低于300Hz的时候图像就不是很清晰，这种现象是预计当中的，是由许多原因引起的，例如齿轮的不圆度对信号的影响等等。

选取数据文件292，此时的齿轮处于过度破损状态，图4a和b是其原始信号和频谱图，图4c和d是其TSA信号和频谱图，图4e和f是其TSA信号的连续小波变换幅值图和相位图。

图4a为齿轮箱振动信号的时域波形，存在很强的背景噪声，难以看到周期的冲击信号。图4b原始信号的频谱中很难看出振动信号的转频和啮合频率，因此难以确定故障情形。从图4c中可以明显的看到70个波峰和70个波谷对应70次啮合，但波形不是很光滑，有明显的破损现象;而且在旋转角度270度附近可以看到振幅相对增大。再观察图4d中TSA信号的频谱，可以看到主要频率分量 fm=613Hz，即啮合频率，同时也存在 2阶频 2fm=1226Hz，及3阶频3fm=1839Hz，高频噪声已基本消除。但可以看到2阶、3阶频率的幅度有一定的增加。很明显，齿轮破损后，啮合频率以及各次谐波振动分量的幅值都会有所上升。由于其信号的幅值增加的不是很明显，因此基波成分幅值增长较慢，而使信号逐渐趋近于方波形式，导致各次谐波分量幅值增长比基波要快的多。从图4e中可以发现在旋转角度270度附近的啮合频率处能量有一定的波动，这表明该位置的轮齿已经出现磨损或破损现象。图4f与正常齿轮TSA信号的连续小波变换相位图相比有一定的不规则性，但此时还很难判断齿轮的故障信息。

图4 数据文件292的振动信号

选取数据文件298，此时的齿轮处于断裂状态，齿轮状态为从动轮有1个轮齿已部分断裂。图5a和b是其原始信号和频谱图，图5c和d是其TSA信号和频谱图，图5e和f是其TSA信号的连续小波变换幅值图和相位图。

图5 数据文件298的振动信号

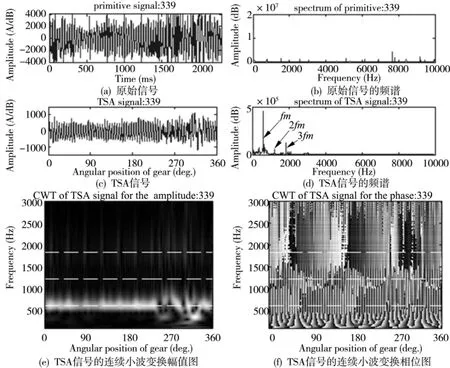
图6 数据文件339的振动信号

由于此时的齿轮已经发生断裂现象，存在很强的噪声与干扰信号，图5a齿轮箱振动信号的时域波形产生严重的波动，图5b原始信号的频谱在高频区的波动也明显加大。从图5c TSA信号中可以看到在旋转角度270度附近振动幅值有一个明显的增长，说明在这个位置齿轮的轮齿已经发生破裂。观察图5d中TSA信号的频谱，可以看到主要频率分量即啮合频率、以及2阶、3阶频率的幅度有明显的增加，说明由于齿轮轮齿破裂引起齿轮箱振动加强。在图5e中可以发现故障状态的齿轮在旋转角度270度附近的啮合频率处能量有很大的波动，能量突增突减，这表明该位置的轮齿已经出现断裂。在两个齿轮啮合的过程中，齿轮之间存在碰撞，由于两个齿轮的轮齿是相同的，因此碰撞的力也是相同的，在齿轮存在断裂的情况，断裂的轮齿啮合时影响不是很明显，因为轮齿更加灵活，但当断裂的轮齿啮合后正常轮齿进入啮合区时就会产生很大的冲击，从而引起幅值的波动。从TSA信号的连续小波变换幅值图中能清晰的看到齿轮断裂的现象，但从图5f TSA信号的连续小波变换相位图中却很难判断齿轮的轮齿已经发生断裂。

数据文件339是所采集的最后一个数据文件，此时的齿轮处于严重故障状态，齿轮状态为从动轮有5个轮齿完全断裂，2个轮齿部分破裂。图6a和b是其原始信号和频谱图，图6c和d是其TSA信号和频谱图，图6e和f是其TSA信号的连续小波变换幅值图和相位图。

图6a为齿轮箱振动信号的时域波形，信号在特征频率或其它某个频率处的能量明显增加，这是由于齿轮的磨损、点蚀、变形、破裂等因素的影响，使得齿隙增大，重合系数减小，轮齿变薄，刚度下降，齿廓变形，所有这些因素都会使齿轮在运行中振动的幅值增加，振动信号的能量增加。但很难直接从信号的时域波形辨别信号所代表的齿轮运行状态。在图6b原始信号的频谱中存在许多被旋转频率和噪声信号调制的边频带，各种频率的频谱相互重叠，使频谱图变得紊乱，有用的故障信号完全被淹没，很难识别故障对齿轮箱振动信号的影响。从图6c TSA信号的波形图中，可以在旋转角度270度附近看到明显的脉冲现象，而且振动加强，信号的幅值明显增加。图6d的频谱中可以看到在啮合频率613Hz，以及2阶、3阶频率附近有明显的边频带，而且较之数据文件298的频谱，可以发现边频带数量多，幅值大，分布宽。在图6e中，可以看到在旋转角度270度和315度附近能量波动很大，这表明此处已经有几个轮齿断裂，这时齿轮已经有5个完全断齿，2个局部断齿。图6f TSA信号的连续小波变换相位图与图3f正常齿轮相比是不规则的，在水平轴接近于270度的位置有一个类似于分叉的过渡，这个信号频率是细长的，比1倍的齿轮啮合频率要高，比1.5倍的齿轮啮合频率要低，这个过渡是齿轮轮齿断裂的象征，但不是很明显。

4 结束语

(1)时域同步平均可以有效的提取与齿轮振动信号直接相关的周期信号，消除噪声和非相关的干扰，提高了分析的信噪比，利用连续小波变换的方法对TSA信号进行分析是一种很有用的信号分析和预处理方法。

(2)信号的频谱分析能有效观察齿轮振动信号的频谱结构，及齿轮出现故障时反应在频谱上的多个边频带。但对于具体边频带特征却难以识别，使得对齿轮故障难以诊断，利用连续小波变换对TSA信号进行进一步分析便可达到齿轮箱故障诊断的目的。

(3)通过TSA信号的连续小波变换幅值图和相位图对齿轮箱振动信号进行对比分析，发现齿轮箱振动信号的小波变换幅值图能较早的揭示故障信息，而且更加清晰。

(4)通过试验与分析可以发现，TSA信号的连续小波变换方法对于检测磨破损、有细小裂纹、以及断裂的齿轮状态非常有效。

［1］李国华，张永忠.机械故障诊断［M］.北京:化学工业出版社，1999.

［2］杨国安.机械设备故障诊断实用技术［M］.北京:中国石化出版社，2007.

［3］周伟.MATLAB小波分析高级技术［M］.西安:西安电子科技大学出版社，2006.

［4］丁康，李巍华，朱小勇.齿轮及齿轮箱故障诊断实用技术［M］.北京:机械工业出版社，2005.

［5］G.DALPIAZ，A.RIVOLA，R.RUBINI.Effectiveness and sensitivity of vibration processing techniques for local fault detection in gears［J］.Mechanical Systems and Signal Processing，2000，14(3):387-412.

［6］H.Zheng，Z.Li，X.Chen.Gear fault diagnosis based on continuous wavelet transform［J］.Mechanical Systems and Signal Processing，2002，16(2-3):447-457.

［7］G.DALPIAZ，A.RIVOLA.Condition monitoring and diagnostics in automatic machines:comparison of vibration analysis techniques［J］.Mechanical Systems and Signal Processing，1997，11(1):53-73.

［8］张德丰.MATLAB小波分析［M］.北京:机械工业出版社，2009.

［9］D.BOULAHBAL，M.FARID GOLNARAGHI，F.ISMAIL.Amplitude and phase wavelet maps for the detection of cracks in geared systems［J］.Mechanical Systems and Signal Processing，1999，13(3):423-436.

Fault Diagnosis for Gearbox Based on Wavelet Transform

XU Ying-shuai，WANG Xi-yang，SUN Wei
(School of Aeronautical Manufacturing Engineering，Nanchang Hangkong University，Nanchang 330063，China)

The Time Synchronous Averaging(TSA)signal where the only constituent frequencies signal are the gear meshing frequency signal and harmonics signal.If the gear faulted，the TSA signal will have modulations.This paper applied continuous wavelet transform to the TSA signal of gearbox vibration，to test and analyse the teeth defect of gearbox.A gearbox fault diagnosis test-bed was made，and a data acquisition system was designed on the basis of LABVIEW to collect vibration signals during meshing experiment of the whole gear life cycle.Then drawing out the corresponding signal waveform by MATLAB program，and making signal analysis and processing，in order to achieve the gearbox fault diagnosis and verify the effectiveness of gear fault diagnosis.

fault diagnosis;gearbox vibration;TSA signal;continuous wavelet transform;signal analysis and processing

TH132;TP206;TP274

A

1001-2265(2012)02-0066-06

2011-06-29

航空科学基金(2010ZD56011);人事部留学人员科研择优资助项目(DB200903036);南昌航空大学科技创新团队项目(EB200906296)

徐英帅(1984—)，男，哈尔滨人，南昌航空大学硕士研究生，主要从事机械传动系统状态监测与故障诊断、振动信号处理等方面的研究，(E-mail)xuyingshuai@126.com。

(编辑 李秀敏)