灰色GM(1,1)幂模型初始条件的组合优化
王正新,党耀国,裴玲玲
灰色GM(1,1)幂模型初始条件的组合优化
王正新1,党耀国2,裴玲玲2
(1.浙江师范大学经济与管理学院,浙江金华321004;2.南京航空航天大学经济与管理学院,江苏南京210016)
针对GM(1,1)幂模型求解初始条件的优化问题,提出一种基于原始序列新旧信息的线性组合优化方法。在模拟误差平方和最小化的目标下,构建初始条件组合权重的优化模型,给出最优组合权重的解析式。最后以中国高中升学率的数据为例,验证了此优化模型的有效性和优越性。结果表明初始条件优化方法能够有效地平衡新旧信息的权重,并提高GM(1,1)幂模型的模拟和预测精度。
灰色系统;GM(1,1)幂模型;初始条件;组合优化
一、引 言
作为灰色系统预测和控制理论的核心模型,近年来,GM(1,1)模型已经为国内外学者所认可[1]301。目前,在模型改进和实际应用方面都取得了很多有价值的研究成果[2-6]。然而,无论如何改进GM(1,1)模型,它的预测函数始终是单调递增或衰减的,因此,对于非线性特征较强的原始数据,该模型并不适用。这是限制GM(1,1)模型进一步推广应用的突出问题。
灰色GM(1,1)幂模型是近两年发展起来一种新型灰色模型,其主要优点在于灰色作用量中的幂指数能够较好地反映原始数据的非线性特征,因而可用于描述和预测事物非线性发展态势。然而过去很长一段时间里,人们并未注意到GM(1,1)幂模型的应用价值,主要原因就在于该模型的求解较GM(1,1)模型和灰色Verhulst模型更加困难。王正新等人利用灰色系统信息覆盖的思想首次给出了幂指数的白化公式,提出了GM(1,1)幂模型的求解方法,并讨论了幂指数的不同取值范围对模型解的性质的影响[7]。李军亮等人将GM(1,1)幂模型的应用范围拓展为非等间距序列,并采用粒子群算法求解模型,取得了较好的应用效果[8]。王丰效以白化微分方程为基础,利用梯形公式白化灰导数,得到了一种改进灰导数的GM(1,1)幂模型[9]。王正新等人基于误差来源分析,提出了无偏GM(1,1)幂模型,该模型对传统GM(1,1)幂模型及其本身的时间响应函数所表达的曲线进行模拟和预测具有重合性[10]。
上述对GM(1,1)幂模型的改进均是从灰色微分方程的角度出发的,而模型求解的初始条件也是影响灰建模精度的重要因素之一。由于传统解法认为,序列的第一个数据代表系统发展的初始状态,应该以此为初始条件求解微分方程。然而,这却违背了邓聚龙教授提出的“新息优先”原理[1]。党耀国等人以序列中最新的数据x(1)(n)作为初始条件建立GM(1,1)模型,这种方法充分利用了新信息,取得了较好的预测效果[11]。我们认为,这种思路对改善模型对未来的预测精度是有帮助的,但是,我们也难以从理论上严格证明以x(1)(n)作为初始条件一定会取得比以x(1)(1)作为初始条件更好的预测结果。
基于以上的分析,本文考虑以序列的第一个数据x(1)(1)和最后一个数据x(1)(n)的某种线性组合作为GM(1,1)幂模型的初始条件,并建立优化模型求解最优的组合权重,以期取得更高的建模精度。
二、GM(1,1)幂模型的定义
设非负原始序列为X(0)=(x(0)(1),x(0)(2),…,x(0)(n)),对原始序列X(0)作一阶累加生成(1-AGO),得序列:
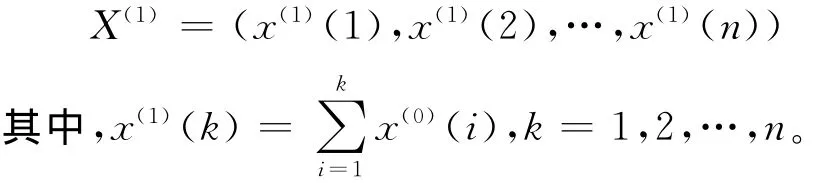
对序列X(1)作紧邻均值生成(Neighbor Generation),得序列:
Z(1)=(z(1)(2),z(1)(3),…,z(1)(n))
其中,z(1)(k)=0.5(x(1)(k)+x(1)(k-1)),k=2,3,…,n。
定义1[7]设X(0)为非负的单峰原始数据序列,X(1)为X(0)的1-AGO序列,Z(1)为X(1)的紧邻均值生成序列,则有满足灰建模三条件的如下非线性模型,称

为GM(1,1)幂模型。
其中,γ≠1,GM(1,1)幂模型发展系数a、灰色作用量b,以及幂指数γ均为未知参数。当γ=0时,GM(1,1)幂模型为GM(1,1)模型;当γ=2时,GM(1,1)幂模型为灰色Verhulst模型。γ的具体计算公式见王正新等人的研究[7]。
得到幂指数γ的估计之后我们便可以根据式(1)对参数列(a,b)T作最小二乘估计

为GM(1,1)幂模型的白化方程。
定理1[7]设B,Y,^a如定义1所述,^a=(a,b)T=(BTB)-1BTY,则

2.GM(1,1)幂模型x(0)(k)+az(1)(k)=b(z(1)(k))γ的时间响应序列为
^x(1)(k+1)=
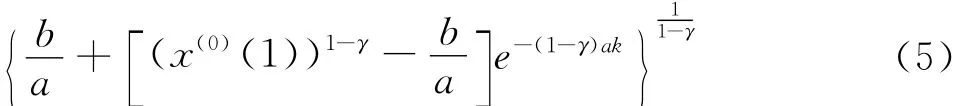
其中,k=1,2,…,n
3.还原值

选择不同的初始值将会直接影响到最终的模拟预测结果。下面将研究给定幂指数γ的情况下,GM(1,1)幂模型初始条件的组合优化问题。
三、GM(1,1)幂模型初始条件的组合优化
不妨先给出GM(1,1)幂模型白化方程解的一般表达式:
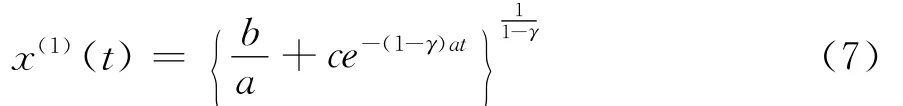
若取初始条件为x(1)(1),GM(1,1)幂模型的时间响应式为式(5);
若取初始条件为x(1)(n),GM(1,1)幂模型的时间响应式为:

其中,k=1,2,…,n。
下面考虑引入一个参数β来组合这两种初始条件,以体现新旧信息在初始条件中的重要性,β∈[0,1]。
当取式(7)中的t=1时,

当取式(7)中的t=n时,

分别用β和1-β乘以式(9)和式(10):

于是,
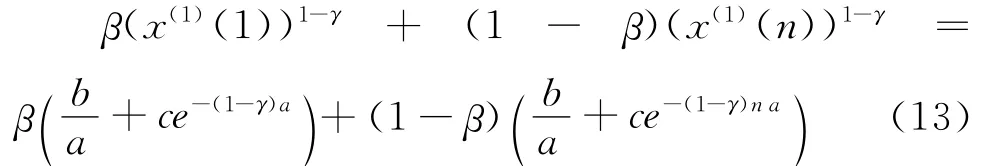
由式(13)解得:
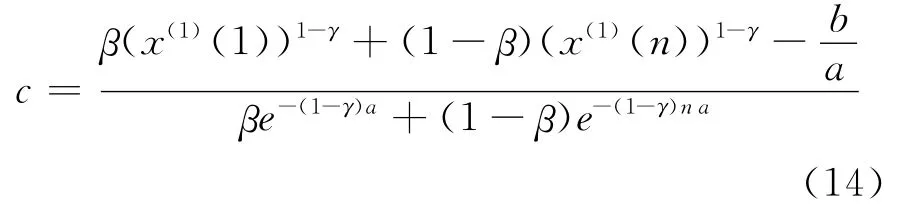
确定参数c,使得
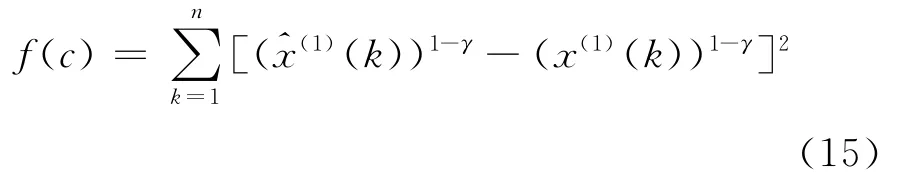
达到最小。

解式(16)得:

由公式(14)和(17)可知

解式(18)得初始条件的加权系数:

因此,GM(1,1)幂模型优化的时间响应式为
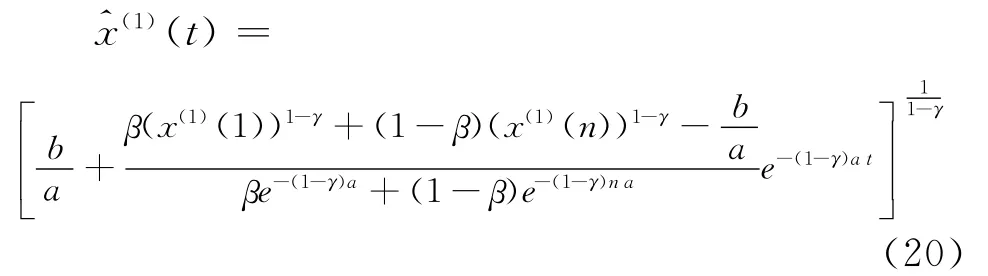
当β=1时,式(20)等价于式(5),即以x(1)(1)为初始条件的时间响应式;
当β=0时,式(20)等价于式(8),即以x(1)(n)为初始条件的时间响应式。
四、模型检验
将第k时刻的相对误差(Relative Percentage Error)记为RPE(k),其公式为

所有时点的相对误差平均值(Average Relative Percentage Error)记为ARPE,其公式为

对于给定α,当ARPE<α且RPE(n)<α成立时,称模型为残差合格模型,一般取α=5%。
五、应用实例
近20年来,中国经济有了长足的发展,在国际上的地位有了很大的提高,扩大高等教育的规模是势所必然的,中国高等教育也正朝着大众化的方向发展。高中升学率为普通高校招生数(含电大普通班)与普通高中毕业生数之比,该指标是反映高等教育发展的重要指标。自从1999年中国实施扩招政策以来,高中升学率呈现出先增长后下降的单峰特性(见表1),由王正新等人的研究结论[7]可知,宜采用GM(1,1)幂模型进行模拟和预测。下面利用本文提出的优化方法对中国高中升学率进行模拟和预测,同时与王正新等人提出的幂指数优化方法[12]进行精度比较。

表1 1999-2008年中国高中升学率(%)
(一)幂指数优化方法[12]
利用参数之间的关系构建优化模型,得幂指数的最优值γ*=0.294,取^x(1)(1)=X(1)(1)=63.8,可得时间响应式^x(1)(k+1)=(187.631 7-168.832 9e-0.08298k)1.4165;k=1,2,…,9。
(二)初始条件组合优化方法
根据式(19)计算初始条件为x(1)(1)和x(1)(n)的组合权系数:
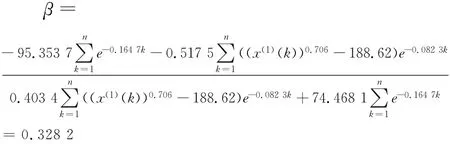
可见,新信息x(1)(n)的权重大于x(1)(1)。
将β值代入式(20),得GM(1,1)幂模型优化的时间响应式为:

累减还原值为

注意到,优化初始条件的GM(1,1)幂模型的初始条件不再是x(1)(1),因此,此处的模拟增加了1999年的数据作为比较。两种模型的精度比较见表2。
由表2可以看出,本文优化模型和幂指数优化方法的平均模拟误差(ARPE)分别为1.26%和1.20%,均小于5%,可见两者均为残差合格模型,但是本文优化模型的精度略高于幂指数优化方法。在对2007和2008两年数据的预测方面,本文提出的优化模型也具有明显的优势。主要原因就在于本文提出的优化模型考虑了新旧信息在初始条件中的最优权重。
六、结 论
初始条件是影响灰色系统建模精度的关键因素之一。无论是以序列的最旧数据x(1)(1)为初始条件,还是以序列中最新的数据x(1)(n)为初始条件,都难以获得高精度的建模结果。由本文构建的组合优化模型求出的权重能够平衡新旧信息在预测中的作用,从而有效地提高GM(1,1)幂模型的模拟和预测精度。

表2 两种优化模型的精度比较表
[1] 邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002.
[2] Wang Y F.Predicting Stock Price Using Grey Prediction System[J].Expert Systems with Applications,2002,22(8).
[3] Xie N M,Liu S F.Discrete Grey Forecasting Model and Its Optimization[J].Applied Mathematical Modelling,2009,33(4).
[4] Li D C,Yeh C W,Chang C J.An Improved Grey-Based Approach for Early Manufacturing Data Forecasting[J].Computers &Industrial Engineering,2009,57(5).
[5] 薛小荣,党小刚.基于灰色理论的西安土地利用预测研究[J].统计与信息论坛,2009,24(11).
[6] 曾波,刘思峰.近似非齐次指数增长序列的间接DGM(1,1)模型分析[J].统计与信息论坛,2010,25(8).
[7] 王正新,党耀国,刘思峰,等.GM(1,1)幂模型求解方法及其解的性质[J].系统工程与电子技术,2009,31(10).
[8] 李军亮,肖新平,廖锐全.非等间距GM(1,1)幂模型及其应用[J].系统工程理论与实践,2010,30(3).
[9] 王丰效.改进灰导数的GM(1,1)幂模型[J].纯粹数学与应用数学,2011,27(2).
[10]王正新,党耀国,练郑伟.无偏GM(1,1)幂模型及其应用[J].中国管理科学,2011,19(4).
[11]Dang Y G,Liu S F.The GM Models that x(n)be Taken as Initial Value[J].Kybernetes,2004,33(2).
[12]王正新.含可变参数的缓冲算子与GM(1,1)幂模型研究[D].南京:南京航空航天大学博士学位论文,2010.
Combinatorial Optimization of the Initial Value in GM(1,1)Power Model
WANG Zheng-xin1,DANG Yao-guo2,PEI Ling-ling2
(1.School of Economics and Management,Zhejiang Normal University,Jinhua 321004,China;2.College of Economics and Management,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)
In view of the optimization problem of the initial value in GM(1,1)power model,this paper puts forward a linear combinatorial optimization method based on new and old information of original sequence.A combinatorial optimization model for the weights of initial values is constructed with the objective of minimum simulation error sum of squares.The analytical expression of the weights of initial values is proposed.Finally,the superiority and effectiveness of the new methods is illustrated by the data of the promotion rates from senior secondary schools to higher education in China.The results show that the initial condition optimization method proposed in this paper can effectively balance the weights of old and new information and improved the simulation and prediction accuracy of GM(1,1)power model.
grey system;GM(1,1)power model;initial value;combinatorial optimization
book=55,ebook=83
N941.5
A
1007-3116(2012)06-0055-05
(责任编辑:马 慧)
2011-12-24
国家自然科学基金项目《基于灰色理论的小样本振荡序列预测方法及其应用研究》(71101123);全国教育科学“十一五”规划青年课题《“十二五”期间中国大学生失业预警研究》(EIA100402)
王正新,男,江苏高邮人,管理科学与工程博士,讲师,研究方向:预测与决策理论。

