异方差White检验应用的几个问题
刘 明
异方差White检验应用的几个问题
刘 明a,b
(兰州商学院a.统计学院;b.甘肃经济发展数量分析研究中心,甘肃兰州730020)
White检验通常由LM检验来完成,现实中也可以使用更简单的F检验来替代LM检验;White检验过程中需要构筑辅助回归模型,它可以有不同的形式以应对实际问题的需要;讨论了四类不同的辅助回归模型,理论分析表明,它们在应用中各有所长;最后通过一个实际例子,验证了理论分析的结论,展示了White检验应用的灵活性。
异方差;White检验;辅助回归模型
异方差是计量经济学中所讨论的一个重要问题,异方差的检验方法在异方差问题的讨论中居于核心地位。在线性回归模型中,异方差的检验方法有很多,依据不同的前提条件,这些检验又各有所倚。在诸多异方差检验方法中,最有效、最常用的当属White检验了,这种检验方法提出以后,以其快捷的检验过程和有效的检验结论而得到广大学者的认可,并迅速成为异方差检验的经典方法。笔者在计量经济学课程教学过程中发现,White检验是初学者的一个学习难点,很多初学者只懂得White检验的思路和方法,而不会对其加以灵活应用。本文将对White检验的使用技巧进行总结提炼,为初学者提供学习便利,为研究者提供借鉴。
一、White检验方法概述
White检验是Halbert White在1980年提出的,他在随机项存在异方差的情形下,构造出参数估计量方差协方差矩阵的一致估计,并根据这个估计结果,导出了一个服从χ2分布的统计量,即拉格朗日乘数(LM),用此统计量可完成异方差的检验[1]。在统计学中,通过构造LM统计量进行的检验也可简称为LM检验。为避免繁杂的数学推导公式,这里借用普通教科书中的关于White检验的表述内容,并以此作为讨论的开始。对于更严谨的、一般化的论述,可参见Halbert White所述[1]。
White检验基于这样的一个前提:随机干扰项的异方差和解释变量有关。经验证明这是合乎实际的。以二元线性回归模型为例的White检验方法如下[2]413-414:
设二元线性回归模型:

该模型存在异方差:var(μi)=
第一步,构造检验辅助回归模型:
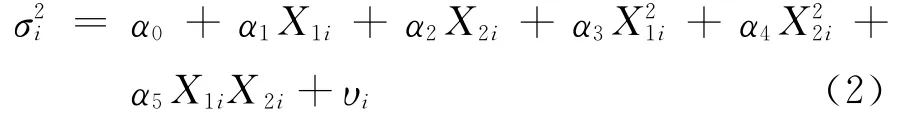
式(2)表明随机项的方差受到解释变量的影响。
第二步,提出假设H0∶αi=0,(i=1,2,3,4,5),即原模型不存在异方差;H1∶αi(i=1,2,3,4,5)不同时等于零,即原模型存在异方差。
第三步,估计辅助回归模型。首先用OLS方法估计式(1)得到残差ei并取平方得e2i,再利用e2i估计出辅助回归模型。进一步计算出辅助回归模型的多重可决系数R2。
第四步,构造并计算检验统计量nR2,即拉格朗日乘数。该统计量服从自由度为约束条件个数的χ2分布。式中n为样本容量,R2为辅助回归模型的多重可决系数。此处约束条件个数为5。
第五步,做出检验决策。如果nR2大于χ2分布上自由度为5的上端100α%的临界点χ2α(5),则拒绝原假设。
以上即为异方差White检验的基本过程。在现实应用中,针对具体的情况和检验要求,可以做出不同的处理。下面将基于上述检验过程,讨论在具体问题中如何灵活应用White检验。
二、White检验应用的多样性分析
在实际问题中,White检验可以演化为不同的检验形式,在不同情形下对这些检验形式也有着不同的要求,下面对这些具体的检验方法做出分析。
(一)White检验中的统计检验方法
White检验通过构建反映随机项的方差和解释变量之间关系的线性回归模型即辅助回归模型,并利用LM检验方法来检验辅助回归模型的显著性,依此判断原模型是否存在异方差。这里使用的LM检验属于χ2检验范畴。LM检验的对象是辅助回归模型的偏回归系数全部等于0,注意到辅助回归模型是一个线性模型,由此可知,这里所检验的就是辅助回归模型的整体显著性,原假设可看成是辅助回归模型的偏回归系数等于零所形成的线性约束条件。对此,White在他的论文中使用了LM检验,而事实上,也可以用一个更为简单的检验来替代,那就是F检验。
仍以上述二元回归模型为例,针对辅助回归模型所构造的原假设仍然为αi=0(i=1,2,3,4,5),显然,这5个线性约束条件表明所检验的是模型整体的显著性,由此可以构造F统计量:

其中ESS、RSS分别为辅助回归模型的回归平方和及剩余平方和,5、n-6分别为它们各自的自由度。接下来即可根据F检验方法来完成检验决策,因此用F检验替代LM检验亦可完成White检验。
(二)White检验中辅助回归模型的构造
在White检验中,构造辅助回归模型是检验的核心环节,White在其论文中提出的辅助回归模型在现实应用中即为:用原始模型的残差平方对原始模型中的解释变量、解释变量的平方和解释变量的交叉乘积进行回归所建立的回归模型。在二元回归中所构建的辅助回归模型如式(2)所示。这类辅助回归模型涵盖的信息全面,考虑到了异方差出现的多种可能途径,同时对这些可能的出现途径也有着明确的展示,在大样本的前提下,用此类辅助回归模型所得到的检验结论是极具说服力的。但是,这类辅助回归模型由于待估参数较多而造成了模型自由度的损失,例如,在三元回归模型的异方差检验中按上述方法构建的辅助回归模型的参数个数是10个,而在四元回归模型中就达到了15个。在此情形下就会降低辅助回归模型估计的精度,进而对检验结论造成不利影响。
为避免参数个数较多而造成的辅助回归模型自由度损失的问题,可以考虑简化辅助回归模型,一般的做法是剔除模型中的解释变量的交叉乘积项,从而减少了参数的个数,降低自由度损失的影响。在二元回归模型中,剔除交叉乘积项的辅助回归模型为:

不难发现模型中参数的个数减少了一个。如果原模型中有更多的解释变量,参数的个数会减少得更多。
继续考察辅助回归模型(2),其解释变量是原回归模型的解释变量、解释变量的平方和解释变量的交叉乘积。如果考虑使用原回归模型的解释变量的线性组合来重新构造辅助回归模型,则又会产生一种新的构造辅助回归模型的办法。以二元回归模型为例,具体方法是:
首先估计出原始模型(1),得到残差ei并进而得到e2i,同时得到被解释变量Yi的估计值:


式(4)即为所构造的辅助回归模型。对于式(4)存在这样两个特点:一是参数个数较式(2)大幅减少,事实上,按此法构建的辅助回归模型的参数在任何情形下都只有3个;二是式(4)中的解释变量囊括了式(2)中的所有解释变量,只要将^Yi=^β0+^β1X1i+^β2X2i代入式(4)即可看出这一点。对模型(4)实施F检验或LM检验即可以完成White检验。
(三)White检验中辅助回归模型的选择
通过上述讨论可以发现,White检验中的辅助回归模型可根据不同的研究视点构造出式(2)、式(3)和式(4)三种形式,应用中可根据不同的研究需要加以选择。式(2)的优点在于,涵盖信息全面,能够发现异方差变动的路径,但模型中包括的参数较多,易造成自由度的损失,形成相应的缺点;式(3)在一定程度上解决了自由度损失的问题,但由于丢失了一部分解释变量而使得信息不够全面——实际上是通过牺牲更多的信息来源,以弥补自由度的损失;式(4)解决了由于参数过多而造成的自由度损失的问题,提高了检验结果的可靠性,同时它也没有从根本上丢弃交叉乘积项——它将所有的解释变量都隐含在^Yi和^Y2i中了,但式(4)却无法表述异方差和原模型解释变量之间的具体联系,同时,拟合的^Yi实际上相当于对X1、X2、X21、X22、X1X2等解释变量形成了约束,进而使得式(4)估计结果的可靠性降低,不利于异方差进一步的解决。
根据上述三类辅助回归模型的优缺点分析,不难得出如下简单结论:如果样本容量足够大,自由度的损失不会影响估计结果和检验结果,则辅助回归模型选择式(2);如果样本容量不够大,同时还需要构造异方差和解释变量之间的关系,则式(3)可委曲求全;若样本容量较小,同时只想检验异方差是否存在而不关注其具体的形式,则式(4)较为可靠。如果检验的目的仅在于是否存在异方差,而不关注异方差和解释变量的关系,笔者认为下述辅助回归模型亦较为可靠:
lne2i=ä0+ä1ln^Yi+πi(5)
其中πi是随机项。式(5)中e2i、^Yi取对数的原因有:一是降低数据的波动,减少异方差对其估计结果的影响;二是^Yi取对数后在一定程度上包括了其他次幂的信息。对于式(5)的显著性检验借助于t统计量即可完成,更方便快捷。
(四)White检验对解决异方差问题的作用
异方差问题的解决通常需要借助于加权最小二乘法,而实施加权最小二乘法的关键是确定权重。加权最小二乘法的权重在理论上是随机项方差的倒数,但在实际应用中随机项方差是未知的,因而需要对权重进行构造,用已知量加以估计。现实中是通过估计随机项方差关于解释变量的函数来构造权重,即:
σ2i=f(X1,X2,…,Xk)
如果用e2i代表随机项方差,则可以利用辅助回归模型式(2)构造函数f的估计结果,将1/f作为权重,加权最小二乘法即可顺利实施,异方差问题便得到解决。这一过程将在文中下一部分的例证中予以展示。
三、基于2009年中国各省、市、区人均GDP变动的考察:一个应用实例
为了展示异方差White检验的灵活性和实用性,笔者收集了2009年中国各省、市、区人均GDP、人均消费、人均投资等宏观经济指标的数据,构建了反映人均GDP变动的线性回归模型,利用此模型对上述理论分析内容做出实证展示。

表1 2009年中国各省、市、区人均GDP、人均消费、人均投资数据表 单位:万元/人
用PGDP表示人均GDP,PC表示人均消费,PI表示人均投资,则以PGDP为被解释变量,PC、PI为解释变量的线性回归模型的估计结果为①需要指出的是,这里所构建的模型未必是正确的,例如它没有考虑到进出口的影响,但这并不影响本文的研究目的和分析结论。:

通过各项统计检验指标可以看出,模型拟合结果较好;通过进一步考察表明,模型未受到多重共线性的干扰,同时模型也不存在空间自相关问题。下面利用White检验法来检验该模型是否存在异方差,检验思路是:同时使用F检验和LM检验对前文所构造的四类辅助回归模型进行检验,以比较彼此间在过程上和结果上的差异。
首先利用辅助回归模型式(2)进行异方差检验。辅助回归模型的估计结果为:

可以看出,无论是LM检验还是F检验,都拒绝了同方差的假定。
再利用辅助回归模型式(3)进行检验,其估计结果为:

估计结果式(8)也得到了拒绝同方差假定的结论。值得注意的一点是,式(8)的整体拟合效果优于式(7),这说明在样本容量不是充分大的条件下,剔除辅助回归模型的交叉乘积项对于其估计结果来说是有利的。
辅助回归模型式(4)的估计结果如下:

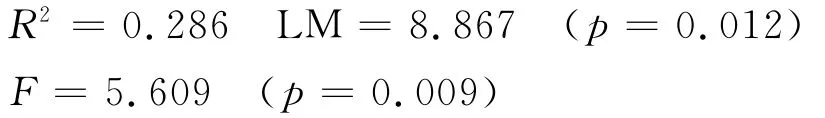
估计结果式(9)同样表明原模型存在异方差。式(9)整体上非常显著,这由LM及F统计量即可看出,但也应注意到,对于单个参数的估计结果,t检验是不显著的。
利用辅助回归模型式(5)对原回归模型作异方差检验,根据其回归系数的t检验结果得知,原模型存在异方差。式(5)的估计结果如下:

各类检验结果均表明,原模型存在异方差问题,可以使用加权最小二乘法对其加以解决。首先需要构建权重。按前文表述,可以依据辅助回归模型式(2)的估计结果来构造权重的表达式。通过估计结果式(7)可以看出,随机项的方差(由式(6)的残差的平方来表示)的变动主要和PIi、PI2i有关,因此可构建如下回归模型:

式(11)拟合效果较好。^e2i是PIi和PI2i的线性组合,可以用它的倒数1/^e2i作为所估计的权重。为了保证权重的非负性,可以在运算过程中取其绝对值。用式(11)所得到的权重1/^e2i对原模型进行加权最小二乘估计,估计结果如下:

模型各项统计检验均通过,拟合效果较好。该模型的残差和残差的平方变动都较为平稳,对此模型进行异方差检验发现没有异方差问题。因此,以为权重的加权最小二乘法很好地解决了异方差的问题。
笔者也试着根据辅助回归模型式(4)(其估计结果为式(9))构建权重,对原模型进行加权最小二乘估计,但得到的估计结果不甚理想。
四、结 论
异方差White检验的思想和使用过程均不复杂,在现实中可以灵活应用。通过分析研究表明,异方差White检验可以使用经典的LM检验方法,也可以借助于F检验来完成,因为检验目标都是辅助回归模型的整体显著性;在White检验中,可以根据不同的前提条件(例如样本容量)和检验目的(例如是否考察异方差的变动)来构造不同的辅助回归模型,以满足研究的需要,文中所讨论的四类辅助回归模型在不同的场合中都有各自的优势,使用时可以根据实际加以选择;White检验的一个显著的优点在于,可以利用辅助回归模型探寻随机项方差与解释变量之间的关系,并据此构造加权最小二乘法中的权重函数,以有效解决存在异方差问题的线性回归模型的参数估计问题。所有上述观点均在文中最后的例证中得到了充分的论证和展示。
[1] Halbert White.A Heteroscedasticity-Consistent Covariance Matrix Estimator and a Direct Test of Heteroscedasticity[J].Econometrica,1980,48(5).
[2] Gujarati Damodar N.Basic Econometrics[M].Fourth ed.New York:McGraw-Hill,2004.
Some Application Problems of White Heteroscedasticity Test
LIU Minga,b
(a.School of Statistics;b.Gansu Economics &Development Quantitative Analysis Institute,Lanzhou University of Finance and Economics,Lanzhou 730020,China)
It is true that White test is usually done by LM test,but we also can use the F-test to replace the LM test in reality.It need to build an auxiliary regression model during the proceeding of White test,and it can take different forms in response to practical needs.It discusses four types of different auxiliary regression models in the paper,theoretical analysis showed that every of them has its own advantage.In finally we show a practical example to verify that the conclusions of the theoretical analysis,and show the flexibility of White test in application.
heteroscedasticity;White test;auxiliary regression models
book=45,ebook=92
O212
A
1007-3116(2012)06-0045-05
(责任编辑:崔国平)
2012-02-18
刘 明,男,安徽霍邱人,经济学硕士,讲师,研究方向:统计理论与方法,经济计量分析。

