微分改进RBF网络线性预测控制算法的研究
张 燕 邓 嫔 张佳会 杨 鹏
(河北工业大学控制科学与工程学院,天津 300130)
0 引言
近年来,对基于线性系统的建模和预测控制理论的研究取得了很大的进步。当被控对象存在弱非线性时,采用该线性预测控制算法非常有效。实际系统存在非线性时变、强非线性等因素,基于局部线性化或局部线性近似的方法是常用的处理方法[1-3]。但由于未充分考虑误差的积累所带来的超调影响,系统的稳定性较差,预测输出与实际偏离较大。神经网络是对非线性系统建立预测模型和优化控制的关键技术之一。各种基于神经网络的预测控制算法虽然本身也存在一定的缺点,但它有效的综合控制性能使其具有很好的发展前景[4]。
受传统PID控制中微分控制作用和模型线性化的启发,本文对性能指标函数进行改进,并提出了微分改进的RBF神经网络线性预测控制方法。该算法对预测控制算法进行反向优化,能实时给出优化控制量,具有操作简单、控制量给出迅速和优化跟踪效果好等特点。
1 非线性系统辨识
非线性系统可用以下非线性离散时间模型表示:
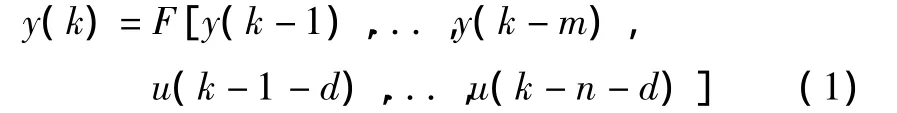
式中:y(k)和u(·)分别为k时刻非线性系统模型的输出和输入;m和n分别为输出量和输入量的阶次;d为滞后时间,假设d=0;F(·)为一个未知的连续非线性函数,可以用一个神经网络来逼近,其表达式如下。

式中:FNN为一个神经网络函数,它在整个建模过程中是不变的(k)为该网络的辨识输出值,它可通过训练,逼近实际输出值y(k)。
径向基函数(RBF)神经网络是具有单个隐含层的三层前馈网络,它由输入层、隐含层和输出层三部分组成。其主要特点是从输入层到隐含层的映射是非线性的,隐含层到输出层的映射是线性的。该网络的表达形式简单,在加快收敛速度的同时能避免局部最优问题,从而达到较高的辨识精度,因而在实际工程中得到广泛应用。RBF神经网络结构如图1所示。

图1 RBF神经网络结构图Fig.1 Structure of RBF neural network
图1中,输入节点数为N=m+n;网络的输入向量X=[x1,x2,...,xN]=[y(k -1),...,y(k - m),u(k -1),...,u(k - n)];H=[h1,h2,...,hL]T为网络的径向基向量;W 为网络的权值向量,W=[w1,w2,...,wL]。
hj为核函数,核函数的种类很多,但最常用的是高斯核函数,其表达式如下:

式中:hj为网络中第j个隐含层节点的输出;Cj为高斯函数的中心向量,Cj= [cj1,cj2,...,cjN];δ 为网络的基宽参数,δ = [δ1,δ2,...,δL],δj为大于0的标准化常数。RBF神经网络的输出为隐含层节点输出的线性组合[5-8]。

2 带微分项的RBF神经网络
设在k时刻,系统的实际输出值为y(k),RBF神经网络辨识输出值为(k),神经网络辨识的目的是通过训练,使辨识输出逼近实际输出。在考虑误差变化率对系统影响的情况下,假设辨识器的性能指标函数为:
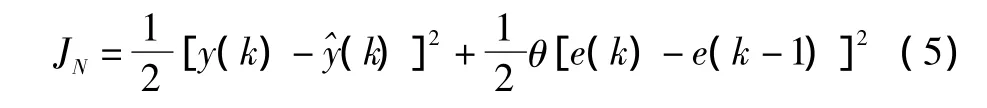
从式(3)和式(4)可以看出,需确定的RBF神经网络参数有权向量W、中心矢量Cj、基宽度参数δ和隐含层的节点数L。对于基宽度参数δ、中心矢量Cj和权向量W的调整,采用的是基于Delta学习规则的梯度下降法。
权向量W调整为:
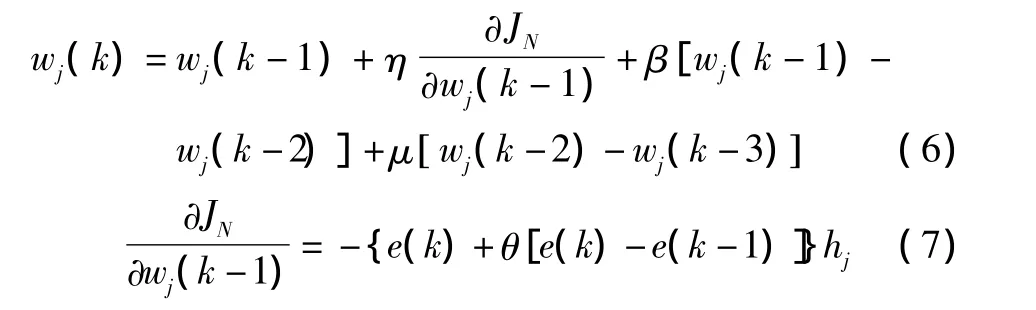
基宽度参数δ调整为:

中心矢量Cj调整为:

式中:β和μ为动量因子;η为学习速率;且0<η<1。
3 微分改进RBF网络线性预测
不论算法的形式如何,基于神经网络的预测控制都包含预测控制的三个基本部分:预测模型、滚动优化和反馈校正[9]。微分改进RBF神经网络线性预测控制就是直接采用辨识网络作为预测模型进行向前一步预测;然后通过线性化逼近未来输出设定值,利用未来输出设定值和实际输出值,预测增量值和误差校正值之间的关系;最后通过反向优化的方式求得当前时刻的最优控制量。在k时刻,利用局部线性逼近的方法对辨识输出值(k)进行线性逼近,从而得到辨识输出值(k)对网络输入变化的灵敏度信息[10-11]。

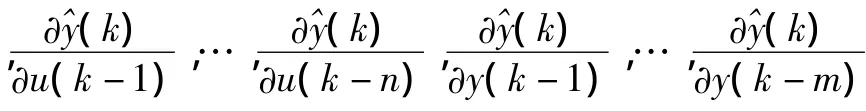

在式(12)的基础上,假设k时刻向前一步的预测增量值可用下式表示:

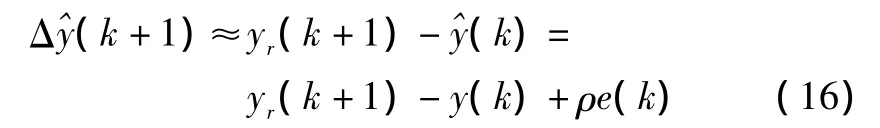
式中:ρ为误差变化因子,它是一个实常数。
结合式(15)和式(16),得到当前k时刻的控制量表达式为:

4 神经网络预测控制算法步骤
根据上述推导,可以得到神经网络预测控制算法的步骤如下[12-14]。
①根据控制对象选择神经网络的初始化参数;
②利用取得的系统输入输出样本数据,并结合式(3)~式(12),对非线性系统进行离线辨识训练,通过训练得到合适的基宽度参数δ、中心矢量Cj和权向量W;
⑤ 用系统的参考轨迹yr(k+1)代替(k+1),根据式(17),求得控制量的增量Δu(k)和当前控制量的增量u(k);
⑥ 优化性能指标函数JN,利用式(6)~式(10),对基宽度参数δ、中心矢量Cj和权向量W进行在线调整;
⑦将得到的u(k)作为受控对象的控制信号输入,计算实际的输出y(k+1);
⑧在下一时刻转至第③步,重新计算,并不断地调整控制信号。
5 仿真实例
为了验证方法的有效性,选取文献[13]中的非线性系统模型:

采用RBF神经网络进行训练时,选取隐含层数L=9,输入节点数 N=4,动量因子 β =0.05、μ =0.01,学习速率η=0.1,微分加权因子θ=0.1,设定未来输出值序列为方波信号。不带微分项和带微分项的辨识效果分别如图2所示。

图2 辨识效果Fig.2 Recognition effect
从图2可以看出,带微分项的RBF神经网络具有较好的辨识跟踪能力,能很好地抑制超调。将训练好的RBF神经网络应用到系统辨识和控制量的求解中,误差变化因子ρ=-0.45。
设定未来输出值的序列为方波信号,得到的控制效果如图3所示。

图3 控制效果Fig.3 Control effect
从图3可以看出,实际输出曲线能够很好地跟踪设定输出,跟踪曲线没有超调,且收敛较快。
6 结束语
在传统性能指标函数的基础上,本文对微分改进RBF神经网络预测控制算法进行了改进,加入了误差微分项。从辨识结果可以看出,系统的超调量减少、调节时间缩短,系统的控制性能得到改善。利用辨识模型作为预测模型,通过对输出设定值进行线性逼近的反向优化算法,实时给出优化控制量,避免了复杂的非线性求解。通过非线性系统仿真实例,验证了所提方法的可行性和有效性。
[1]陈增强,袁著祉,张燕.基于神经网络的非线性预测控制综述[J].控制工程,2002,9(4):4 -11.
[2]陈增强,车海平,贺江峰,等.基于神经网络的二次逼近非线性自适应预测控制器[J].电路系统学报,1998,3(1):26 -32.
[3] Miguel A B,Ton J J,Van D B.Predictive control based on neural network model with I/O feed back linearization[J].International Journal of Control,1999,72(17):1358 -1554.
[4]戴文战,娄海川,杨爱萍.非线性系统神经网络预测控制研究进展[J].控制理论与应用,2009,26(5):521 -526.
[5]刘金琨.智能控制[M].北京:电子工业出版社,2005.
[6]朱海洋,张莉.RBF神经网络PID控制在分切机中的应[J].自动化仪表,2009,30(12):68 -71.
[7]冯冬青,徐学红,费敏锐.神经网络广义预测控制在锅炉燃烧系统中的应用[J].自动化仪表,2006,27(6):18 -21.
[8]方益民,徐保国.RBF神经网络在压力校验台数据非线性校正中的应用[J].自动化仪表,2005,26(10):28 -29.
[9]许超,陈治纲,邵惠鹤.预测控制技术及应用发展综述[J].化工自动化及仪表,2002,29(3):1 -10.
[10]张燕,陈增强,袁著祉.基于Taylor逼近的非线性系统PID型多步预测控制[J].控制与决策,2004,19(4):448 -451.
[11]张世峰,李鹏.基于神经网络的自整定PID控制器设计[J].自动化仪表,2009,30(7):64 -66.
[12]Zhang Yan,Liang Xiuxia,Yang Peng,et al.Modeling and control of nonlinear discrete-time systems based on compound neural networks[J].Chemical Engineering,2009,17(3):454 -459.
[13]刘金琨.先进PID控制 MATLAB仿真[M].2版.北京:电子工业出版社,2006.
[14]飞思科技产品研发中心.Matlab7神经网络理论与实现[M].北京:电子工业出版社,2005.

