基于极化分解的极化特征参数提取与应用
王庆,曾琪明,廖静娟
(1.北京大学遥感与GIS研究所,北京100871;2.中国科学院对地观测与数字地球科学中心,北京100094)
基于极化分解的极化特征参数提取与应用
王庆1,曾琪明1,廖静娟2
(1.北京大学遥感与GIS研究所,北京100871;2.中国科学院对地观测与数字地球科学中心,北京100094)
基于极化分解原理,获取了描述地物散射机制的特征参数,并组合成一些特征指数,如雷达植被指数等。这些特征指数具有反映体散射信息的能力,从而可间接获取植被长势、疏密程度及分布区域等信息。实验选择了鄱阳湖区Radarsat-2全极化数据,结合野外采集的样本数据,在分析该区植被特征的基础上,对不同特征参数进行了对比分析,对雷达植被指数与实地测量样本的生物量参数进行了相关分析。实验结果表明:文中给出的4种特征参数对植被引起的随机散射的描述总体趋势是一致的,但随着植被覆盖密度的增大,不同特征指数具有一定的差异,其中雷达植被指数最为准确,适用动态范围最大,并且与湿地植被生物量具有较高的线性相关性,可以定量地反映研究区的植被疏密及生物量差异信息。
非相干分解;极化分解;散射机制;雷达植被指数
0 引言
合成孔径雷达(synthetic aperture radar,SAR)具有全天候、全天时对地观测的能力,全极化SAR(polarimetric SAR,Pol-SAR)对地观测可获取地物散射回波的能量、相位和极化信息[1]。雷达波在与地物作用时受地物结构影响,原发射电磁波的极化状态会发生变化,极化SAR可获取各极化通道的相位和幅度参量信息。这是利用极化SAR数据提取地物结构等信息的基础。相比光学遥感仅能获得植被冠层光照的特点,极化SAR具有电磁散射矢量特性和微波穿透性等优势,对森林和农作物等植被的分布、结构及长势状况等信息可反演得更准确。但极化SAR研究多集中在极化分解[2]和电磁散射模型[3-4]等方面。为了有效快速地应用极化SAR数据,还需借鉴光学遥感(如植被指数)构建极化SAR特征参数并研究其应用,发挥极化SAR具备的优势。利用全极化SAR数据提取或反演植被等目标的相关信息将是目前及未来研究的热点[1-4]。
极化分解技术[5]是研究和应用全极化SAR数据的主要方法,因为极化分解技术本质上分离了地物不同散射机制引起的极化特征,利用各种极化分解方法就可以有效地提取目标地物的主要散射特征,从而实现提取目标地物信息的目的。其中,极化分解包含了基于散射矩阵的相干目标极化分解和基于散射矩阵的二阶矩(协方差矩阵或相干矩阵)的非相干目标极化分解[5]。极化特征参数是基于极化分解技术得到反映目标散射电磁波特征的参数或在这些极化分解参数基础上组合形成的特定指数。利用这些特征参数可以相对容易地解释电磁波与地物之间的相互作用,简化了定量反演地物参数等有关信息的算法。
雷达遥感应用中的自然目标大多为分布目标散射体,其属于非相干目标,可采用非相干极化分解方法对散射体进行统计性描述。常用的非相干分解方法有Freeman-Durden分解[6]、基于特征矢量和特征值的分解[5,7]、H/A/alpha分解[8]及Van Zyl分解[9]等。采用这些分解方法,都可以在一定约束条件下得到反映目标散射特性的定量信息。这些分解方法分别从基本电磁散射物理模型、数学正交分解模型及地物散射模型等角度出发,反演出地物散射回波信息中的单次、偶次和随机散射的强度,以及与地物结构密切相关的参数。本文主要根据Freeman-Durden分解和特征矢量分解方法,分别介绍雷达植被指数、基于Freeman分解的雷达植被指数、Luneburg熵和归一化Pedestal等4个参数的推导及物理含义,并以一景覆盖鄱阳湖湿地的Radarsat-2全极化SAR数据为例,结合研究区植被特点,研究了这些极化特征参数与实际地物覆盖特征的对应关系,并分析这些参数之间的关系,为极化SAR数据高效广泛的应用奠定基础。
1 特征矢量分解与极化SAR的特征参数
1.1 特征矢量分解
根据相干矩阵的特征向量分析,Cloude[5]提出了能包含所有散射机制的分解方法,在分析矩阵群论的基础上,用Pauli基矩阵把散射矩阵分解成4个散射机制的矢量和,它们分别表示各向同性表面散射、二面角散射和交叉极化散射(含2项)。该分解除了能解释全极化SAR图像上地物的物理散射机制外,还具有正交散射机制的优点,因为Pauli基是两两正交的,于是获取的散射机制信息是互相独立的,彼此不相关的。
以Pauli基为分解基,将散射矩阵分解后系数矢量化,得到极化目标矢量k[1-2]及其相干矩阵T3,即
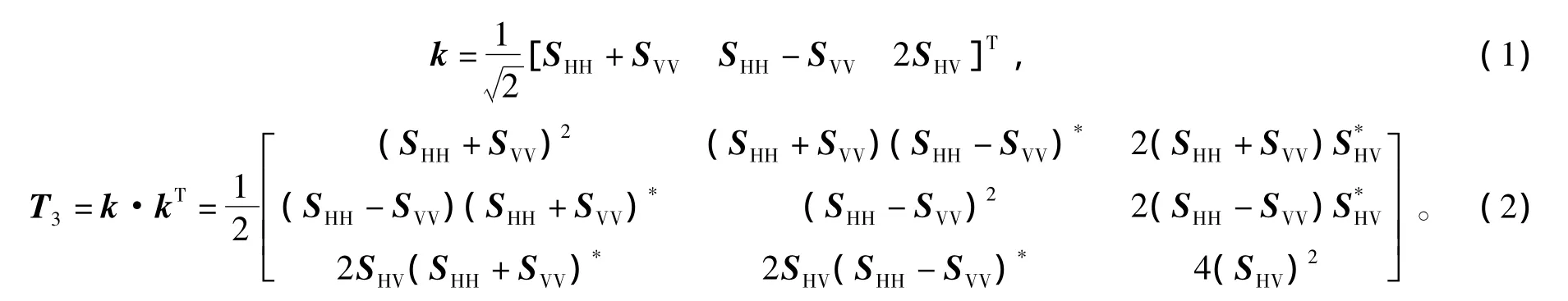
由矩阵论可知,相干矩阵T3为半正定的Hermite矩阵,可以通过酉相似变换进行对角化,即

式中:每个T3i都表示一种散射机制,其对应特征值λi(i=1,2,3)反映了不同散射机制的强度;特征值λi及特征向量ui反映了接收回波中所有散射信息;U3为3个特征向量ui组成的矩阵。由此Cloude[8]定义了反映地物散射回波及与地物组织结构随机性的散射熵[8](H),即
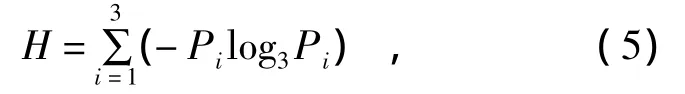
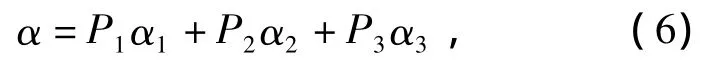
式中αi(i=1,2,3)为特征矢量内部参数。
1.2 极化特征参数
1.2.1 雷达植被指数
Van[9]把树状植被刻画成各种圆柱介质,植被的结构决定了圆柱的大小、疏密和圆柱组合的方向,并应用随机方向的圆柱电介质模型对普通形状的植被电磁散射进行了计算机模拟,分析了植被电磁散射具有的极化特征,发现相干矩阵分解得到的第2和第3特征值与该模型等价,于是给出了一个雷达植被指数(RVI),即
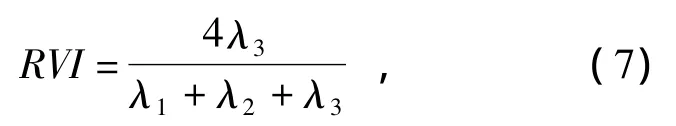
式中:λ1>λ2>λ3;0≤RVI≤4/3;当RVI等于4/3时,对应着较细的圆柱,即植被比较稠密,电磁波与其相互作用时发生完全随机性的散射,入射波在介质内发生了充分的随机散射,致使散射回波完全去极化,3个特征值大小相同;而随着RVI减小至0时(λ3=0),则对应着粗壮的圆柱,即植被的结构较为简单,被刻画成几个简单的圆柱组成,此时散射回波主要是单一散射机制,去极化效应较低(入射波与植被相互作用时发生的随机散射较少),绝大多数入射波都直接经过单次或偶次散射后离开,散射波仍能保持着较好的极化特性。因此,对于简单低密度植被和结构简单的地物如水面、城市建筑、道路及低粗糙的裸地等,RVI是迅速衰减的。
1.2.2 基于Freeman分解的雷达植被指数
Freeman[6]基于3种简单散射机制即奇次、偶次散射和体散射的模型定义了3种散射矩阵,将全极化SAR数据的协方差矩阵分解后得到3类散射机制的功率分量。体散射是指入射波进入植被内部发生了多次散射,其散射回波为随机散射波,它发生了明显的去极化效应。因此,体散射成分越多,则表明该地物去极化特性越显著,回波随机程度越高。本文根据3种分量的比例推导出雷达植被指数。全极化SAR获得的总协方差矩阵C3可以表征3种散射机制的协方差矩阵之和,即
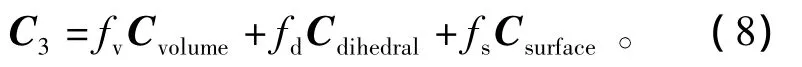
式中:fv,fd和fs分别为体散射、偶次散射和奇次散射3种散射机制模型的贡献权重;Cvolume,Cdihedral和Csurface分别为上述3种散射机制模型的协方差矩阵。于是定义基于Freeman分解的雷达植被指数(RVIFreeman)为
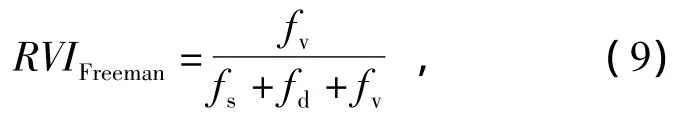
RVIFreeman的取值范围是[0,1]。当雷达波照射区域为裸露地面或面状地物时,因为体散射分量fv趋向于零,所以RVIFreeman的取值也趋向于零;当观测区包含有树林或灌木时,雷达波穿透冠层与地面发生单次散射的能量减小,因此fs将减小;同理,雷达波入射地面反射到树干发生二面角反射的回波也降低,因此fd也将减小;而体散射功率会增大,致使RVIFreeman的取值趋向于1。该雷达植被指数的缺点是Freeman分解未区分粗糙裸地和植被冠层的散射机制,但粗糙裸地的散射强度要远低于植被冠层(特别是浓密植被的后向散射强度),所以对于高密度覆盖的植被区域,RVIFreeman仍具有较好的定量指示意义。这是由于非相干目标极化分解所基于的二阶矩具有表征功率信息的能力。
1.2.3 Luneburg熵
根据特征矢量分解得到的3个特征值,Luneburg[10]定义了目标随机程度算子,即


1.2.4 归一化的Pedestal
由极化合成[1-2,11]的概念可知,在获取目标的散射矩阵之后,可以计算在发射和接收天线任意极化组合下接收到的回波功率;由此得到目标的极化响应图,进行归一化后,对于纯目标而言,其接收功率的范围在[0,1],而对于分布目标而言,其功率归一化最小值>0;由于极化合成中功率P(ψr,xr,ψt,xt)的计算为T3特征值的二次型,即最小的接收功率为最小的特征值项,而最大的接收功率为最大的特征值项,两者系数相同[2];故可推知归一化的极化响应图的基座高度(Pedestal),即

式中λ1≥λ2≥λ3。由于相干矩阵的特征值与最优化的后向散射极化相关,最小和最大的特征值也对应着最小和最大的可接收到的后向散射功率,即当雷达天线适当配置时可得到最小或最大的目标后向散射功率,分别对应着最小或最大特征值。因此,两者之比可反映地物的去极化特性。对纯目标而言,其Pedestal=0,即无去极化特性;对分布目标而言,其Pedestal>0,说明分布目标具有去极化特点;当分布目标的3个特征值相同时,则去极化最大,Pedestal=1。
2 实验数据及实验区植被特征
2.1 数据源与研究区范围
本研究使用一景2010-03-24 T 22:00获取的Radarsat-2标准全极化数据,其中数据范围为E116°05'40″~116°26'46″,N28°49'16″~29°10'25″。图像的空间分辨率为5.4 m×8.0 m(距离×方位向),入射角为30.28°~32.02°(近距~远距),测绘带为25 km×25 km(距离×方位向),具体范围如图1所示。

图1 研究区光学图像、湿地苔草样本及雷达图像Fig.1Optical image,carex samples and SAR image of study area
2.2 实验区植被特征
鄱阳湖湿地植被主要分布于2个区域:水陆过渡区和出露草洲。水陆过渡区内主要为沼泽地,由于紧接水陆分界线,其下垫面为潜育土层,水分饱和,可见残留浮叶植物和一些沼生植被;出露草洲的土层为草甸土,土壤水分较足,生长沼生植物。这2个区域的植被大部分为多年生草本植物,如苔草、芦苇等,覆盖密度大,没有粗壮的茎杆和阔叶,茎叶形态相似,叶片从根部到顶部宽度窄细分布均匀。
雷达波与实验区植被的相互作用可以利用“水云”模型[12]来模拟。总后向散射系数中土壤的单次散射贡献量随着单位体积内植被重量的增大而呈指数级衰减。在植被密集区,总后向散射系数是与植被的后向散射强度近似成正比。
“水云”模型是把植被看成一定高度层状物,内部分布着各种微小粒子和空气分子,粒子的密度反映了生物量的大小。对生物量的估算模型可简化为
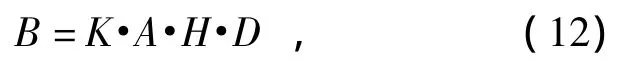
式中:K为常数;A为单位面积,m2;H为冠层的高度,m;D为微小颗粒密度,g·m-3;B为生物量,g·m-2,其与高度和植被颗粒密度的乘积成正比。图2给出了野外采集的样本数据参数,包括单位面积下植被平均高度和植被颗粒密度(单位体积植被质量)与单位面积生物量间的关系。可见生物量与植被颗粒密度的线性相关性更强,这也表明利用“水云”模型的散射机理来解释鄱阳湖苔草植被冠层的后向散射特征是合理的。
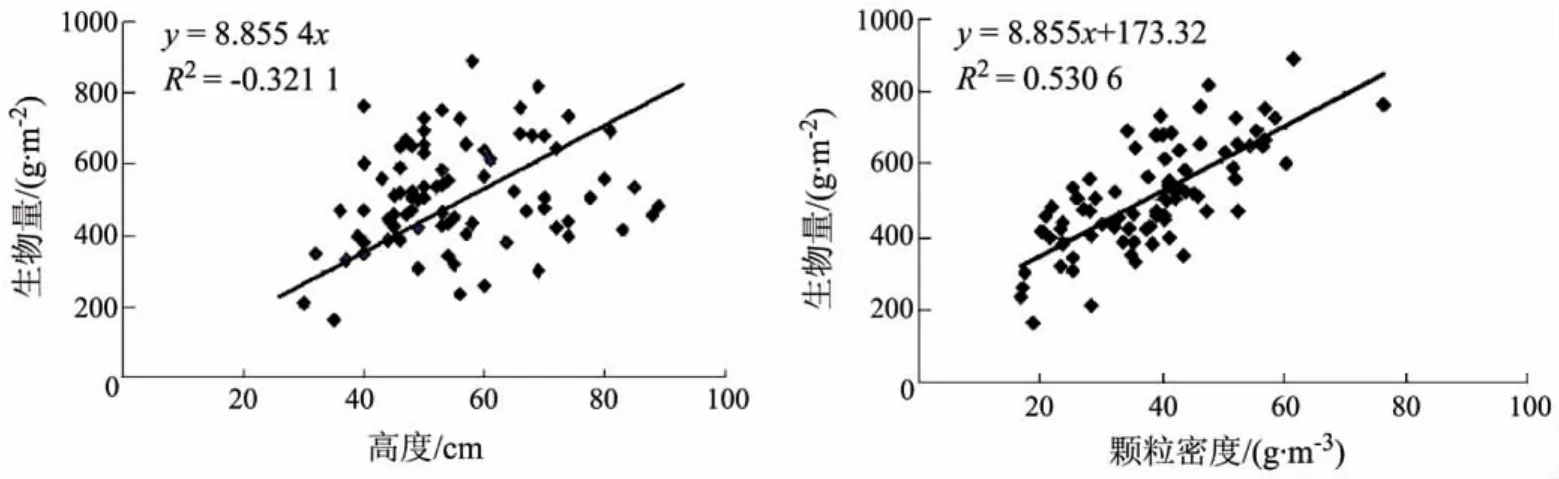
图2 鄱阳湖湿地植被生物量与植被高度、植被颗粒密度间的关系Fig.2Respective correlation between wetland biomass and height,density of the carex in Poyang Lake
3 实验结果与分析
3.1 极化特征参数计算结果
首先根据头文件参数对获取的散射矩阵数据进行辐射定标,继而应用式(1)(2)可得相干矩阵T3及协方差矩阵C3,应用特征值分解和Freeman分解方法求得每个像素对应的特征值及Freeman分解的3个参数。根据1.2节各极化特征参数计算公式得到的结果如图3所示。
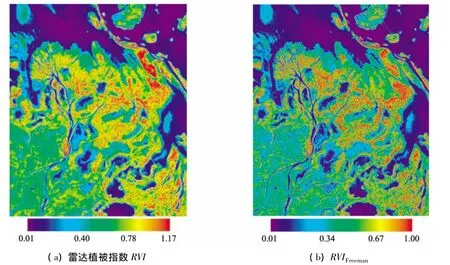
图3 -1研究区4个极化特征参数分布图Fig.3-1Distribution of polarization characteristic parameters of four types in study area
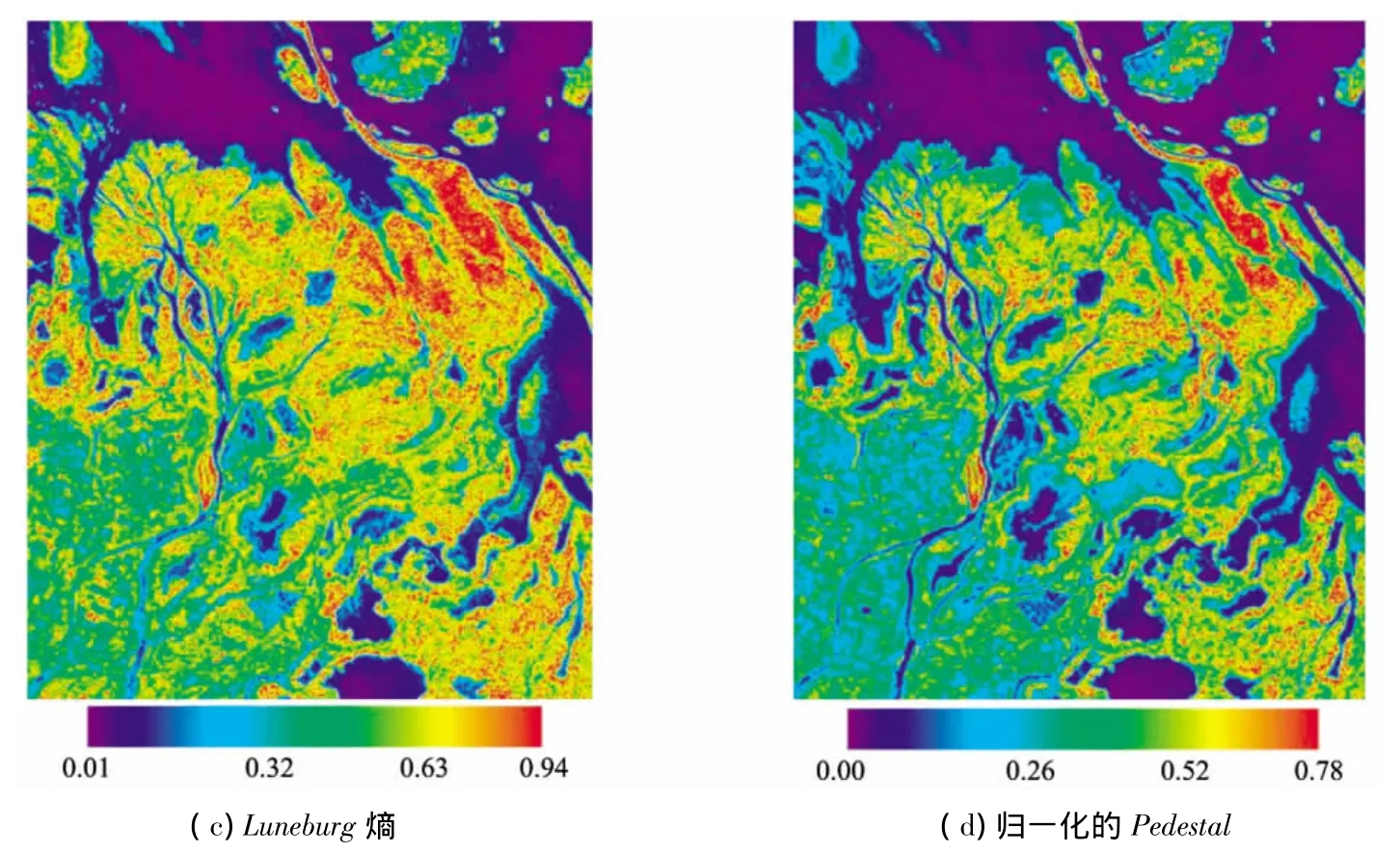
图3 -2研究区4个极化特征参数分布图Fig.3-2Distribution of polarization characteristic parameters of four types in study area
由图3(a)可见,在鄱阳湖各河流入口处(图像中心位置)及附近洲滩地带,绝大多数的RVI>0.7。这是因为该地区分布大量茂密的苔草和芦苇等植被,而图像左下角的农田及城市区域的RVI<0.6,水域的RVI则更低(<0.2)。在一些靠近湖边植被较为密集的区域,其RVI>1.0,如图上呈红色调区域。与此类似,图3(b)—(d)均可见,在植被较密集的洲滩,RVIFreeman、Luneburg熵及归一化Pedestal的数值均接近于1,其色调均趋向红色。而水体、农场区域以及沙滩地,数值趋于减小,色调多为蓝色。因此,这4个极化特征参数反映体散射的趋势是基本一致的,即随着植被密集度的增大,各参数值也相应增大。
3.2 极化特征参数与植被参数相关性分析
3.2.1 极化特征参数与植被覆盖度关系
根据实地调查和图像解译,选择了7个植被密度不同的区域(如中心滩地、湖边等),并将其按疏密程度定性为非常密、高密、中等、低密、一般、稀疏、较稀疏(图4(a))。图4(b)(c)密度分割图绿色区域分别表示雷达植被指数RVI>0.6和基于Freeman分解的雷达植被指数RVIFreeman>0.6,结果与该地区的植被分布基本吻合,但后者分布范围比前者更大。

图4 疏密不同的植被区域及雷达植被指数的阈值分割Fig.4Vegetation region of different density and the segmentation of radar vegetation index
表1为这7个植被疏密不同的区域的特征参数平均值及数值范围,其均值大小趋势与植被疏密程度是呈正比关系。但不同参数的取值范围具有较大差异,其中Luneburg熵与RVIFreeman取值跨度最大,且标准差也很大,说明这2个参数描述地物体散射时非常敏感。
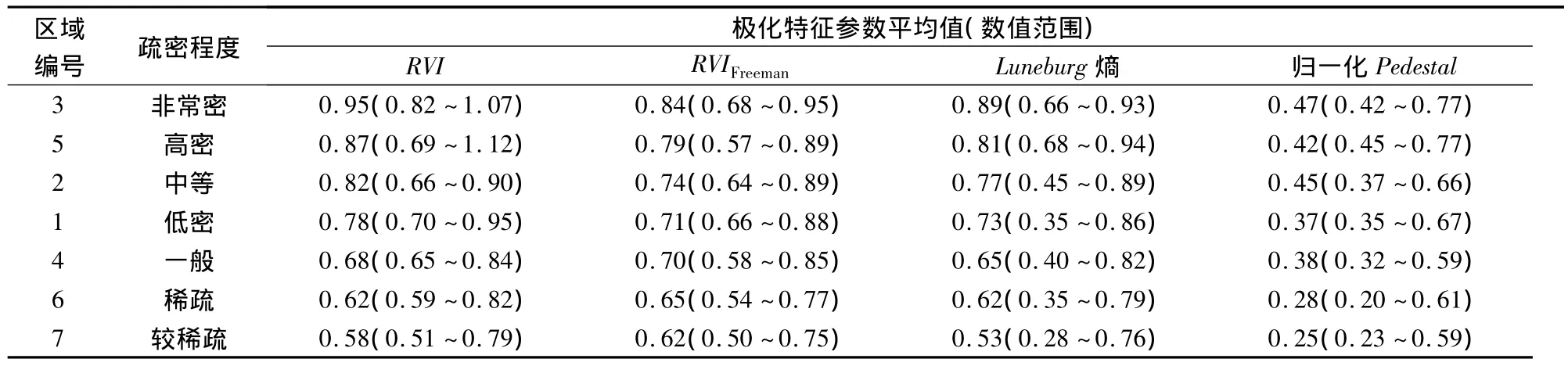
表1 不同区域的极化特征参数平均值及数值范围Tab.1Mean value and range of the characteristic parameters of different areas
3.2.2 极化特征参数与RVI的关系
本文极化特征参数从不同角度反映了地物的散射信息,它们具有各自特点,也有一定的相关性。分析上述研究区的植被数据,得到RVI与其他特征参数之间的关系(图5)。

图5 研究区极化特征参数分别与雷达植被指数的关系Fig.5Correlation between polarization characteristic parameters and radar vegetation index in study area
结果显示:由Cloude[8]提出的H-Alpha平面[8]可知植被的散射熵分布于0.6~0.9之间,结构特别密集复杂(如森林冠层类型)的体散射,其散射熵分布于0.9~1。图5(a)中的散点分布也主要集中在这一“中熵”区域,少部分落入“高熵”0.9~1区域。而且,雷达植被指数与散射熵之间较强相关性可以表明RVI对该区域植被疏密程度的反映是正确的,可以间接地反映植被生物量的信息。理论上,由“水云”模型可知,植被密度的增大,下垫面的散射成分降低,导致了雷达波在植被内部的散射增多,从而对极化入射波的去极化能力显著增强,即交叉极化HV或VH的后向散射功率增强,于是产生的散射熵越大[8],体散射比例越显著,植被密集程度也就越高,因此RVI也相应增大。
图5(b)则反映了Luneburg熵与RVI并没有明显的相关性,但RVI在0.4~1变化区间内,Luneburg熵值绝大多数分布于0.4~0.8区间。因此前文图3(c)所示的结果并不能准确反映植被疏密的定量变化,仅可以定性判断该区体散射等随机散射的强弱。图5(b)显示的Luneburg熵值较大的区域面积较广,主要是因为Luneburg熵在反映植被体散射引起随机性变化的同时,对诸如斑点、二次散射及单次散射相混合时产生的随机性也非常敏感。
由图5(c)可见,归一化Pedestal与RVI的相关性很强,说明其对植被疏密敏感性也很高,会随植被密度的增大极化响应基座高度就越大,即无论极化坐标基如何选择,其最小可接收功率都将增大,但其动态范围相比RVI较小些。
RVI与RVIFreeman的相关性见图5(d)。从图中可知,两者在有些区域相关性很高,但有些区域RVIFreeman数值达到了饱和,而对应的RVI却未饱和。这主要是由于RVIFreeman是基于简单散射模型的推导[6],其分解方法没有保证结果的互不相关性,结果所包含的信息量也有限,不如基于特征矢量分解的结果全面。因此,在一些非植被地物散射区域(如水陆交接处)的粗糙地表(其表面粗糙度和较湿润的地表具有较高的介电常数)散射回波的去极化效应明显,引起的随机散射分量较高,造成了RVIFreeman升高。也就是说,Freeman分解中表征随机散射的散射矩阵模型及协方差模型尚不能区分植被与粗糙裸土的散射特征。
3.2.3 RVI与生物量的关系
在野外同步采集了80个样本点,获得了样本点的RVI与生物量(湿重)间的分布关系(图6(a)),其回归系数为0.402 5,相关系数为0.63;剔除若干异常点后,重新进行最小二乘线性回归后的回归系数约为0.612 2,相关系数达到0.78,且拟合得到的RVI与实际RVI的均方根误差约为0.15(图6(b))。

图6 鄱阳湖地区雷达植被指数与湿地生物量的相关性Fig.6Correlation between radar vegetation index and wetland biomass in Poyang Lake
考虑到SAR图像本身具有的相干斑现象,该相关系数表明雷达植被指数RVI与苔草植被的生物量间具有较强的线性相关性,即与植被疏密程度有较好的相关性。由“水云”模型[12]可知,植被密集区域的“微粒”密度较大,体散射分量较单次散射和二面角散射成分多,因此RVI随植被密度的增大呈递增。鄱阳湖湿地植被在水分充足的洲滩区域生长旺盛,覆盖高度密集,对应的生物量也比较大,其RVI呈现较高的数值,说明图3(a)给出的RVI变化趋势及分布特征与植被生物量相一致。
4 结论
1)极化特征参数是基于极化分解技术得到的反映目标地物散射电磁波特征的参数。分解得到的3个特征值通过一定组合可以获得具有与地物覆盖信息密切相关的特征参数,这些特征参数对于定性解译图像和定量反演地物参数都非常有帮助。
2)雷达植被指数RVI与散射熵、Luneburg熵、归一化Pedestal及RVIFreeman间的对比分析表明,这些参数对于提取雷达波与植被内部发生的体散射信息具有一定的指示意义,其变化趋势总体上是一致的。但雷达植被指数所反映的植被疏密及对应生物量最为准确,其次为与RVI线性相关性高的归一化Pedestal,但其动态范围较小。而RVIFreeman在除高密集植被或高强度的体散射区域外,与RVI也有较好的相关性,Luneburg熵则更多地反映了地物结构的随机性。
3)野外采集样本的数据分析表明,RVI与样本生物量之间具有较强的相关性。对于鄱阳湖湿地苔草这类结构较简单的植被,RVI与生物量变化趋势是一致的,RVI可进一步用于提取植被分布特征信息的提取和植被生物量参数的反演等[13]。
4)本文在Freeman分解基础上所提出的一种新的RVI参数,尚存在对粗糙裸土和植被随机散射区分不足的缺陷。在后续研究中,可根据植被特点适当改进Freeman分解中的植被散射模型,以求更准确地得到反映植被长势、生物量等相关参数的雷达植被指数。
[1]王超,张红,陈曦,等.全极化合成孔径雷达图像处理[M].北京:科学出版社,2008.Wang C,Zhang H,Chen X.et al.Full Polarimetric SAR Image Processing[M].Beijing:Science Press,2008(in Chinese).
[2]Lee J S,Pottier E.Polarimetric Radar Imaging:From Basics to Applications[M].New York:CRC Press,2009:229-262.
[3]Cloude S.Polarisation:Applications in Remote Sensing[M].Oxford:Oxford University Press,2010:178-189.
[4]金亚秋,徐丰.极化散射与SAR遥感信息理论与方法[M].北京:科学出版社,2008.Jin Y Q,Xu F.Theory and Approach for Polarimetric Scattering and Information Retrieval of SAR Remote Sensing[M].Beijing:Science Press,2008(in Chinese with English Abstract).
[5]Cloude S R,Pottier E.A Review of Target Decomposition Theorems in Radar Polarimetry[J].IEEE Transactions on Geoscience and Remote Sensing,1996,34(2):498-518.
[6]Freeman A,Durden S L.A Three-component Scattering Model for Polarimetric SAR Data[J].IEEE Transactions on Geoscience and Remote Sensing,1998,36(3):963-973.
[7]Cloude S R.Target Decomposition Theorems in Radar Scattering[J].Electronics Letters,1985,21(1):22-24.
[8]Cloude S R,Pottier E.An Entropy Based Classification Scheme for Land Applications of Polarimetric SAR[J].IEEE Transactions on Geoscience and Remote Sensing,1997,35(1):68-78.
[9]Van Zyl J J.An Overview of the Analysis of Multi-frequency Polarimetric SAR Data[C]//6th European Conference on Synthetic Aperture Radar(EUSAR 2006).Dresden,Germany,2006:16-18.
[10]Luneburg E.Foundations of the Mathematical Theory of Polarimetry[R]//Final Report PhaseI,N00014-00-M-0152,EML Consultants,2001.
[11]Van Zyl J J,Zebker H A,Elachi C.Imaging Radar Polarization Signatures:Theory and Observation[J].Radio Science,1987,22(4):529-543.
[12]Attema E P W,Ulaby F T.Vegetation Modeled as a Water Cloud[J].Radio Science,1978,13(2):357-364.
[13]廖静娟,王庆.利用Radarsat-2极化雷达数据探测湿地地表特征与分类[J].国土资源遥感,2009(3):70-73.Liao J J,Wang Q.Wetland Characterization and Classification Using Polarimetric Radarsat-2 Data[J].Remote Sensing for Land and Resources,2009(3):70-73(in Chinese with English Abstract).
Extraction and Application of Polarimetric Characteristic Parameters Based on Polarimetric Decomposition
WANG Qing1,ZENG Qi-ming1,LIAO Jing-juan2
(1.Institute of Remote Sensing and GIS,Peking University,Beijing 100871,China;2.Center for Earth Observation and Digital Earth,Chinese Academy of Sciences,Beijing 100094,China)
Based on the polarization decomposition,the authors obtained a set of characteristic parameters to characterize the surface features,and formed some indices by combing these characteristic parameters to extract vegetation growing information such as radar vegetation indexes.These characteristic parameters have the function of reflecting the backscattering information and indirectly obtaining such information as vegetation growing,density and distribution areas.A scene of Radarsat-2 full polarimetric SAR data covering Poyang Lake region was chosen for this experiment and the sample data which included the biomass and vegetation density information were collected in the field at the same time.On the basis of an analysis of vegetation characteristics in this test region,the characteristic parameters were compared with each other and analyzed for their physical meaning.The radar vegetation index and field measurements of biomass sample parameters were statistically correlated.The experimental results show that the four characteristic parameters described in this paper give the same overall trend on the random scattering of vegetation,but different indexes have different indications with the increasing vegetation density,of which the most accurate index is the radar vegetation index,which has the maximum dynamic range.The radar vegetation index has a high linear correlation with the biomass of wetland vegetation,so that it can be used to quantitatively infer the vegetation covering density and the biomass information.
non-coherent decomposition;polarimetric decomposition;scattering mechanism;radar vegetation index
TP 79
A
1001-070X(2012)03-0103-08
王庆(1986-),男,博士研究生,主要从事微波遥感应用研究。E-mail:wangqing_rs@pku.edu.cn。
曾琪明(1964-),男,教授,博士生导师,主要从事微波遥感研究。E-mail:qmzeng@pku.edu.cn。
(责任编辑:邢宇)
10.6046/gtzyyg.2012.03.19
2011-10-08;
2012-01-04
国家863课题(编号:2012AA121304,2008AA121806)和教育部博士点基金(编号:20090001110039)共同资助。

